Contribution to the Fusion of Biometric Modalities by the Choquet Integral

Published Online September 2012 in MECS

The financial stakes of the global electronic information and the need to secure public places are among the major concerns of today's society. Our identity is requested and verified, each time we use an ATM, an Internet Connection or when sending a Mail… We generally use alphanumeric codes, access cards or passwords. However these devices, though simple, can be accessible by other individuals (loss, disclosure, tampering ...) and do not constitute an authentication method for each person by himself [19]. Faced with this increasing solicitation, the verification using the exploration of the intrinsic is one of the most recommended approaches, given the high level of security it provides. Biometrics is a technology for identity verification and/or identification of people. It consists of transforming a biological characteristic (DNA, saliva ...), morphological (face, iris, fingerprint ...) or behavioral (signature, writing, voice ...)

to a digital fingerprint [8]. It is presented as a reliable means of authentication. Convenient, even more difficult to borrow, steal, forget or falsify [7]. However, the performance of authentication systems associated with these biometrics are still weak to even consider their large scale use [18]. In this context, multimodality appears a promising way to improve the performance of a biometric system. However, multimodality poses problems at the level of information fusion.

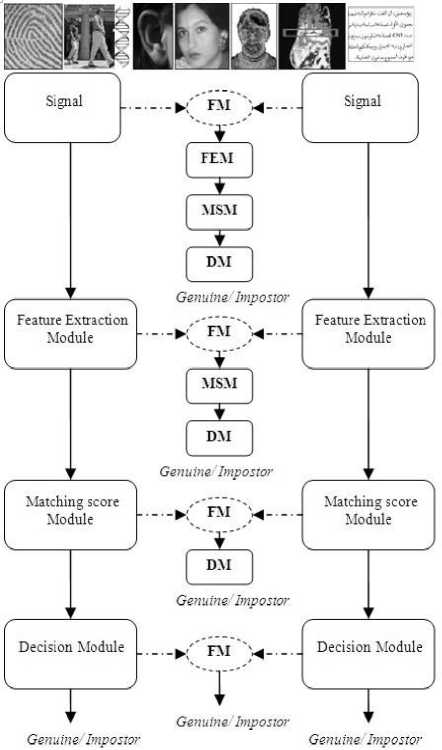
Figure.1 Different levels of fusion on multimodal biometric. FM : fusion module, FEM : feature extraction module, MSM : matching score module, DM : decision module.

The fusion of two or more biometric modalities can be done at four different levels (Fig.1): at Signals level, Features level, Scores level and Decisions level [2, 3].

The fusion signals as well as the characteristics one are relatively not widely used because they are conditioned by the homogeneity of the data, which is generally not verified. Fusion at the decision level involves simple operators such as majority voting, AND and OR to manipulate binary decisions, these fusion methods are relatively simple but they use very little information [17]. The score-level fusion is the fusion type most common since it can be applied to all biometric modalities with a very effective methods like the average, the product, the minimum, the maximum, the weighted average and methods based on the classifiers [1].

In this paper, we propose a biometric authentication system based on the fusion of three modalities never before combined into multimodal biometrics, namely the face, off-line handwriting and off-line signature. We are particularly interested in the technique of fusion of these modalities at the level scores by the Choquet integral. Our choice has been selected based on the Choquet integral because it allows us to take into consideration the interaction between people and modalities [13, 2].

In the following section, we present three unimodal systems based respectively on off-line handwriting, offline signature and face. In Section 3, we give an overview of the Choquet integral and the fuzzy measures. The experiments and the results achieved are detailed in Section 4.

• II.    Unimodal Systems

The three biometric authentication systems respond to the classical scheme of a system of pattern recognition. They are composed of the following: acquisition, characterization, learning and decision. In our work, the features are based on a textual Discret Wavelet transformation using Daubechies9 for face and Symlet6

for off-line signature and off-line handwriting. On the set of features obtained, we have implemented a selection process of the characteristics by the genetic algorithms in order to keep only the most relevant features and to cut out redundant features. The characteristics used for each modality are composed by the mean and the standard deviation from approximation image and the standard deviation of the horizontal details, the vertical details and the diagonal details. For learning, we opted for Support Vector Machines with radial base function. Class-modular classification architecture was adopted [5, 9].

The classification   module is   used during authentication to compare reference characteristics and testing. Thus, each modality returns a similarity score relative to the person to be authenticated. The scores are normalized between 0 and 1 with the MinMax method. However, we use the normalized scores between 0 and 1 where 0 indicates a complete rejection (presence of an impostor) and 1 certain acceptance (presence of a client).

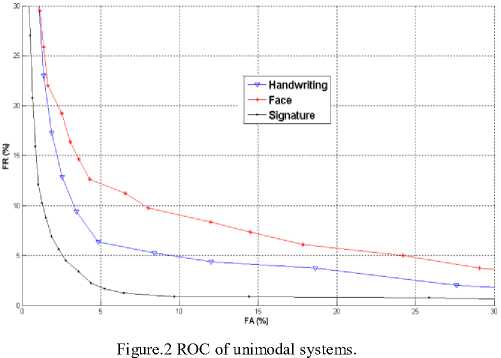
The performance of three unimodal systems is given by Figure 2 for the operating point corresponding to the Equal Error Rate (EER). We note that the performances of the three systems are different, the EER varied from 3.37% for face to 5.87% for handwriting and 9.25% for the off-line signature [2, 4].

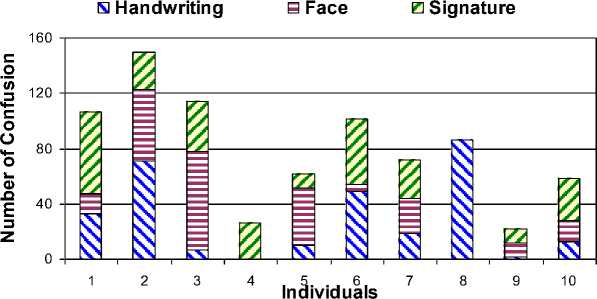
Figure.3 Variation in the number of confusion for a selection of persons of our database.

In Fig. 3, we illustrate the variation in the number of confusion relating to each modality for a selection of individual in our database. We find that the three unimodal systems give quite different results for different people in our database. Thus, we proved that modality can be robust to certain persons but low also to others. Indeed, from the Fig 2, the system unimodal at the base of the face gives better overall performance and it outperforms the other two unimodal systems. However, in Fig 3, we find that for some individuals, the unimodal system based on the writing or the signature gives better performance than the system based on the face.

The traditional fusion techniques (such as the average, the weighted sum, the majority vote or otherwise) do not consider this kind of behavior. Hence the idea of introducing the Choquet integral as a means of aggregation which takes into account this kind of interaction between modalities and the persons [12].

• III.    Choquet Integral and Fuzzy Measure

The Choquet integral has been used as an aggregation tool to calculate an overall score taking into account the importance of criteria expressed by a fuzzy measure in various applications such as [15]: the regulation of multimodal transport systems, graphic symbols recognition, management of human and material resources, air traffic control...

• A.    Definitions

Fuzzy Measure : We call fuzzy measure [6, 11], the function m : P(Y) -> [0, 1] satisfying the conditions (1) and (2):

m ( 0 ) = 0, m (Y) = 1                             (1)

m (A) <  m (B), if A c B and A, B e P(Y)        (2)

m (A) represents the importance or the power of coalition A for the problem of fusion. Following this definition, Sugeno [20] introduced a fuzzy measure m λ which comes with an additional property:

m (A ^ B) = m (A) + m (B) + X m (A) m (B).        (3)

For all (A, B ^c Y), (A ^ B = ⁰ ), and for X>-1, X is determined by solving the following equation :

n

A + 1 = П (1 + m i) i=1

Choquet Integral : Let m be a fuzzy measure of Y. the Choquet Integral C m of a = (a 1 , …, a n ), vector of criteria, is defined by the equation:

n

C_m(a_p...,a_n) = S (a--a-J m ({i,.**^})            (5)

i=1       - with a0 = 0 and a1 < ... < an.

• B. Proposed fuzzy measures

In multimodal biometrics, the performance of modalities can be robust for individuals and weak to others. The Choquet integral can represent perfectly what kind of behaviors through fuzzy measures which are able to express this phenomenon of interaction between biometric modalities and individuals. However, the use of the Choquet integral is not trivial due to the difficulties related to determination methods of the fuzzy measure [22]. According to Grabisch [11], there are no universal methods to determine the fuzzy measure, each application is attributed as the most appropriate fuzzy measure. Several methods have been developed to calculate the fuzzy measure the most appropriate to a given problem, these methods are usually based on an election expert or by optimizing an error criterion [14].

In this paper, we propose a new method for the determination of fuzzy measures. Let D the matrix of scores related to N different modalities N = {1, .., i, .., n} and Z the vector of scores observed during an access of m individuals Z = {z 1 , .., z, .., z m }.

D =

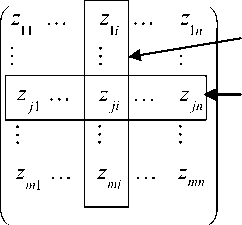
The scores of N modalities related to the j person

The scores of m persons related to the i modality

z ji is the score related to the person ‘ j’ resulting from the ‘ i ’ modality. The word “score” refer to the probability measure or the measure of similarity with that we can recognize the supposed identity of the candidate. The fuzzy measures that we propose are based on; the number of confusion, entropy, and an uncertainty function:

Fuzzy measure based on the number of confusion: the number of confusion is a parameter used to evaluate the accuracy of a classification system by the degree of erroneous decision of the various classes. We exploited the number of confusion committed by each modality to calculate the fuzzy measure. The fuzzy measure m i , related to the ‘ i’ modality is given by (6):

NC mi = в(1  ---L)

NT

With, NC i : number of confusion related to the ‘ i’ modality. NT : the number of total confusion. в : a coefficient of scale ranging from 0 to 1.

Fuzzy measure based on entropy: the entropy is a measure of the quality of information. The Entropy, of a score vector, related to the ‘i’ modality gives the degree of disorder of these scores. We proposed a fuzzy measure based on entropy, related to each modality. It is given by (7):

mi = у Hi ⁽ z h— zmi ) H ( D )

H ( z ,..., z ) is the entropy of the scores, and i 1 i ^{,  ,} mi

( z ,..., z ) is related to the modality ‘ i’ .

m

Hi ⁽ zh ’-’ zmi ) = ^_x zji ^log( zji )

Where H ( D ) is the total entropy of the scores, and / is a coefficient of scale ranging from 0 to 1.

Fuzzy measure based on an uncertainty function: in order to assess the quality of the scores resulting from each biometric modality, we have introduced a function to measure the average of the gap between the scores. The fuzzy measure, based on the uncertainty function, is given by (8):

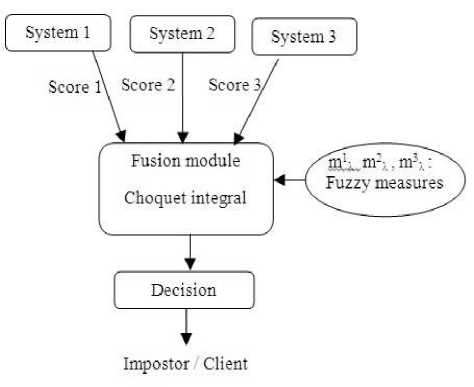
Figure.4 Schema of the fusion of scores by the Choquet integral.

mi

m

S ( z,i" zi )2 j = 1 ^ji i

= a-----------

N

Where z_i is the average score related to the ‘ i ’ modality, a is a coefficient of scale ranging from 0 to 1, and N S is the total number of the scores.

C. Proposed System

Fig. 4 shows the schema of the developed approach. The proposed fusion system has two modules: a module of aggregation of scores based on the Choquet integral and a decision module.

During an authentication session, three scores are presented to merge the module; for each score we have associated a fuzzy measure. The fuzzy measures proposed are based on a statistical study of the number of confusions (Equation 6), entropies (Equation 7) or uncertainty functions (Equation 8).

• IV. Experiments and result analysis

  The experiments were performed on a PC Intel DualCore, 1.73GHz, 1GB RAM, with the environment Matlab R2007 and Visual C++ under the Windows XP platform. To confirm the validity of the proposed fusion approach, we have implemented it on two different multimodal databases. The first database is relative only to synthetic scores. The second is a biometric database relating to face, off-line handwriting and off-line signature.

• A. Synthetic database

In this section, our experiments have been performed on a database related to synthetic scores. Synthetic scores come from three virtual modalities (M 1 , M 2 and M 3 ) corresponding to 60 people (P 1 to P 30 : clients scores, P 31 to P 60 : impostors scores). The scores are normalized between 0 and 1 (table1).

T able .1 SYNHETIC DATABASE

	M 1	M 2	M 3		M 1	M 2	M 3		M 1	M 2	M 3
P 1	0.98	0.98	0.98	P 11	0.6	0.6	0.6	P 21	0.6	0.9	0.1
P 2	0.98	0.98	0.6	P 12	0.6	0.7	0.95	P 22	0.65	0.95	0.15
P 3	0.98	0.6	0.98	P 13	0.6	0.95	0.7	P 23	0.85	0.55	0.3
P 4	0.98	0.6	0.6	P 14	0.55	0.55	0.55	P 24	0.8	0.4	0.6
P 5	0.98	0.7	0.6	P 15	0.9	0.8	0.4	P 25	0.8	0.1	0.6
P 6	0.9	0.8	0.7	P 16	0.9	0.8	0.1	P 26	0.8	0.3	0.3
P 7	0.8	0.8	0.8	P 17	0.8	0.75	0.15	P 27	0.4	0.7	0.8
P 8	0.7	0.9	0.9	P 18	0.7	0.62	0.35	P 28	0.3	0.15	0.63
P 9	0.7	0.7	0.9	P 19	0.68	0.68	0.45	P 29	0.4	0.6	0.35
P 10	0.7	0.9	0.7	P 20	0.75	0.75	0.3	P 30	0.45	0.2	0.25
	M 1	M 2	M 3		M 1	M 2	M 3		M 1	M 2	M 3
P 31	0.1	0.1	0.1	P 41	0.25	0.45	0.4	P 51	0.15	0.4	0.8
P 32	0.1	0.1	0.3	P 42	0.05	0.3	0.05	P 52	0.35	0.7	0.1
P 33	0.1	0.3	0.3	P 43	0.05	0.05	0.3	P 53	0.35	0.55	0.3
P 34	0.4	0.1	0.1	P 44	0.4	0.4	0.6	P 54	0.15	0.65	0.2
P 35	0.4	0.4	0.15	P 45	0.4	0.1	0.6	P 55	0.15	0.55	0.4
P 36	0.4	0.15	0.4	P 46	0.4	0.2	0.75	P 56	0.15	0.55	0.6
P 37	0.4	0.4	0.4	P 47	0.3	0.1	0.55	P 57	0.6	0.3	0.15
P 38	0.25	0.45	0.45	P 48	0.2	0.05	0.65	P 58	0.6	0.55	0.15
P 39	0.25	0.25	0.25	P 49	0.15	0.1	0.55	P 59	0.6	0.15	0.55
P 40	0.35	0.35	0.35	P 50	0.15	0.1	0.7	P 60	0.6	0.55	0.55

The scores were selected to cover all the combinations which may confront a merge module scores. After a thresholding step scores, we considered identical responses (Acceptance / Rejection) for the three modalities and confusion between the responses of a modality with the other two modalities.

To help understand the concept of merging the scores by the Choquet integral, we consider the following example where the fuzzy measure is based on the number of confusion.

Let NC 1 = 8 , NC 2 =12 and NC 3 = 22 are the numbers of confusion relating to modalities M 1 , M 2 and M 3 . The fuzzy measures are calculated through (6): m¹ = 0.433, m² = 0.40, m³ = 0.316. The λ parameter is obtained by solving (4). Following (3), we calculated the fuzzy measures of the subsets as shown in Table 2. The score of the fusion of the three modalities by the Choquet integral is given by (5).

T able .2 FUZZY MEASURES BASED ON THE NUMBER OF CONFUSION.

The subsets of the Modalities	The fuzzy measures
{M 1 }	m1 = 0.433
{M 2 }	m2 = 0.40
{M 3 }	m3 = 0.316
{M 1 , M 2 }	m12 = 0.771
{M 1 , M 3 }	m13 = 0.70
{M 3 , M 2 }	m23 = 0.671
{M 1 , M 2 , M 3 }	m123 = 1

In order to demonstrate the contribution of our approach, we compared the results of the merger by the Choquet integral with respect to classical fusion techniques (AND, OR, PROD, Mean and Majority Voting). Performance is given in Table 3.

T able .3 C omparison of the recognition rate obtained for the

PROPOSED METHODS AND OTHER TECHNIQUES WELL KNOWN IN