Control and Synchronization of Hyperchaotic System based on SDRE Method

Published Online June 2014 in MECS

An interesting phenomenon of nonlinear systems is chaos. In recent years, studies of chaos and hyperchaos generation, control and synchronization have attracted. Therefore, various effective methods have been proposed one the past decades to achieve the control and synchronization of chaotic system, such as Robust Control [1], the sliding method control [2], linear and nonlinear feedback control [3], adaptive control [4], active control [5], backstepping control [6] and generalized backsteppig method control [7-9], ect. The purpose of the present work lies in the design of a robust optimal control system for the control and synchronization of new hyperchaotic system using the state-dependent Riccati equation (SDRE) method. The State-Dependent Riccati Equation (SDRE) techniques are general design methods that control problems involving nonlinear systems [10-14]. For a nonlinear system a form of linearization is required which is not an approximation but simply a rewriting of the mathematical model in a different form. This form, which is not unique, is then possible to obtain feedback control laws.

The rest of the paper is organized as follows: In section 2, a new hyperchaotic system is described. In section 3,

stability conditions in new hyperchaotic system are derived by SDRE method. In section 4, the stability conditions in new hyperchaotic system with uncertainly are derived by robust optimal method. In section 5, synchronization between two new hyperchaotic systems are achieved by SDRE method. Finally, section 6 isprovided conclusion of this work.

II. Hyperchaotic System

Recently, Dadras and Momeni proposed the new hyperchaotic system [15]. The system is described by:

̇=-

̇2=-

̇з=      - dx₃ + gx_Tx₄

̇4=    -ℎx2(1)

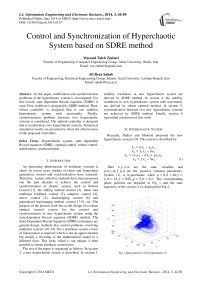
Here X , У , z , w are the state variables and a , b , c , d , f , g ,ℎ are the posotive constant parameters. System (1) is hyperchaotic when a =8, b =40, = 2, d =14, f = 0.05, g =5,ℎ=0.2 . The corresponding phase portraits are depicted in Fig 1 and the state trajectory of the system (1) is displayed in Fig 2.

-50

-100

x2

-50

-100   -100

-50

x1

Fig. 1.phase portraits of the hyperchaotic (7).

Fig. 2.state trajectory of the hyperchaotic (7).

Now, system (1) is described by state dependent Riccati equation (SDRE).

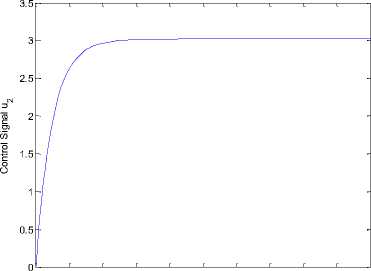
states for system (3) is shown in Fig 3. The time response of control inputs uv u2 is shown in Fig 4.

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

-1

i     а -Хз 00

2 — Х3 -Ь 0

3     СХ2

4     0 -h0

III. Stabilization of hyperchaotic system

In this section, the SDRE method is applied to stabilize hyperchaotic system (2) with now parameters.

i      а -Хз 0  0   xi     101

'           -   0  0           00

з     СХ 2 0 -dgxi  ^Х з ⁺ 0  0 Ы (3)

4     0 -h 0  /   Х4    01]

Where un u2are control function to be determined for achieving minimize cost function (4).

J — ^ (xt (t)Qx(t) + uT(t)Ru(t))d t(4)

Where

^Q — ^ 4X4 ,^ ^— ^ 2X2               ⁽⁵⁾

A state dependent Riccati equation (SDRE) is the solved at each point X along the trajectory to obtain a nonlinear feedback controller of the form (6), where P(t) is the solution of the SDRE.

и (t) — -k(t)x(t)

к (t) — R" 1BT())P(t)(7)

P(t) + P(t)(4(x(t)) + af) + (4^т(х(0) + a/)P(t) +

Q - P(t)S(t)R~^BWto — 0

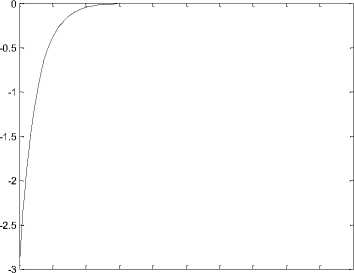
Where scalera is a design parameter [17]. We choose a — 20. As can be seen, the SDRE method produces a stabilizing solution. The time response of xnx 2, x3,x4

Time(Sec)

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

Fig. 3.the time response of signals (x1,x2,x3,x4) for system (3).

-1

-2

-3

-5

-6

-4

System (9) is rewrote as follows:

>̇ 11		Cl - X300	r^i]	10
■ ̇2 ̇	=	Хз -b00	[ ?L +	00
3		cx20-dgxi\		00
̇		0 -ℎ0 f J	Lx4J	01

Вф(9)

Хг Хз X»,

[£]+

-7

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

Fig. 4.the time response of the control inputs (u,u ).

We must find the control signals (6) that it stabilizes the system (12) wwithuncertainly θ 1 ,i=1,2 . This problem is solved by optimal control of system (3) that it minimizes cost function (13) [16].

J =∫ (хт (t) Fx (t)+хт (t)X(t)+ит (t) Ru (t))dt (13)

Where F matrix is

Фт(0)Ф(0)≤F           (14)

F = Фт(0)Ф⁽0)=

S1 00⁰ 000⁰ 000⁰ 000 02 J

90000 0

= 0000

0 00900

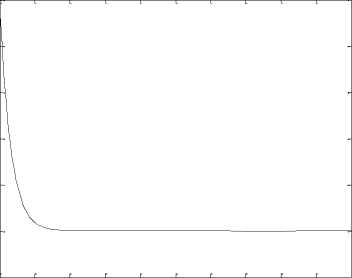
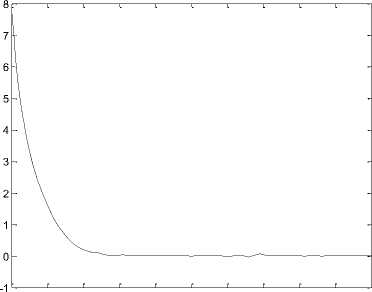
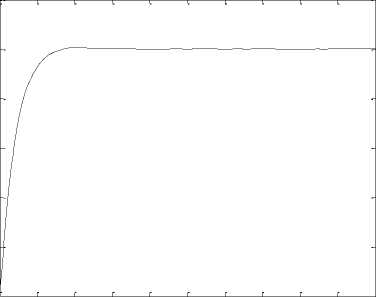
Again, the Riccati equation is solved and the optimal feedback control (6) is obtained. The time response of x 2_ ,x 2 ,x 2 ,x 4 states for system (9) is shown in Fig 5. The time response of control inputs u 2_ ,u 2 is shown in Fig 6.

IV. Stabilization of hyperchaotic system with

UNCERTAINLY

In practical situations, some or all of system parameter can not be exactly know in advance. We assume the system (3) with uncertainly.

̇11

■

̇

■

̇

̇

а + 01 - х₃ 0 ⁰ х₃ - b 0 ⁰ сх₂ 0- d gxi

0  -ℎ0/+ 02

[ ; ]

+

0₀][ и, ] (9)

Where θ2_,θ2 are uncertainly in system and θ1 ∈ [0,30], i=1,2 . Now, robust controller is designed by presented method in [16]. For this reason, states matrix is analysed as follows:

[+ 01 -х3001[ х3 -b00

схг 0-

0  -ℎ0/+ 020

-х300

-b00

0-dQXi

-ℎ0 /

]=

Ф(е)=вФ(е)

Where

^{ф( 6} )=[ ₀ 0₀0₀ 0 ]

0     0.2    0.4    0.6    0.8     1     1.2    1.4    1.6    1.8     2

Time(Sec)

-1

2.5

1.5

ra

-0.5

0     0.2    0.4    0.6    0.8     1     1.2    1.4    1.6    1.8     2

Time(Sec)

0.5

-0.5

-1

-1.5

-2

-2.5

-3

-3.5

-4

0     0.2    0.4    0.6    0.8     1     1.2    1.4    1.6    1.8     2

Time(Sec)

0.5

-2.5

-3

0     0.2    0.4    0.6    0.8     1     1.2    1.4    1.6    1.8     2

Time(Sec)

V. Synchronization of hyperchaotic system

In this section, the SDRE method is applied to synchronize two hyperchaoticsystem. Suppose the drive system takes the following form

̇=  - з̇ =     - byi

2 ̇ ]_ =      - dz_± + gx_tw_t

̇ ^ =     -ℎУ1             (16)

And the response system is given as follows

^̇2=     ^- У₂2₂⁺ и_г ( t )

3 ^̇ 2=       ^- Ьу₂ ⁺ u₂ ( t )

̇2=      - dz₂ + gx₂w₂ + u₃ ( t )

̇ '2 =     -ℎУ2 + u4 (t)

Where u ,u2,u2,u4 are control inputs. Define state errors between system (16) and (17) as follows

^x =    ^-

6y =   -

^z =   - ew =   - wt(18)

We obtain the following error dynamical system by subtracting the drive system (16) from the response system (17)

Fig. 5.the time response of signals (x,x ,x ,x ) for system (9).

0     0.2    0.4    0.6    0.8     1     1.2    1.4    1.6    1.8     2

Time(Sec)

t ̇ x =     - Cy e_z + 2^1 6y + У16у + «! ( t )

t ^̇ X =     - be_y - Xie_z - ^Z1^X ⁺ u₂ ( t )

< ̇ =     - de_z + ge_xe_w - CX^y - cy^y - g^i^w

^- gw^e_x ^{+ U}3 ( t )

̇ = -ℎ ey + u₄ ( t )            (19)

Error dynamical system (19) is rewrote as follows

̇

[ : ̇_̇ :]=^л[ ::]+Δ^л[ г ]+^в[s]

L_£̇_WJ     L^ew] L^ew] Lu₄j

Where

=

г a - e_z 0 ⁰

e_z - b 0 ⁰

I CCy 0- dS^x I

0 -ℎ0 f J

Δ =

[-

0       Z1

- Z1     0

СУ1 - gw^ - CX-L

=

У1 0

- Xl 0

0- gx^

Time(Sec)

We can rewrite ΔΑ matrix as follows

Fig. 6.the time response of the control inputs (u,u ).

0       zi У1

- Zi    0-Xi0

- cyi - 5^1 - cx^ 0- дх_г

ΔЛ= ф(X )               (22)

Where X=[x,y,z,w]т . Substituting (22) into (20), the error dynamics is obtained.

̇

̇

̇

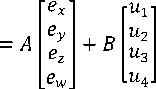
+ ВФ(X )

^x

Су ^z

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9      1

Time(Sec)

We obtain optimal feedback control (6) that it minimizes the cost function (13) [16]. The F matrix is obtained.

F = Фт ( X)Ф(X )=

[У1 + Z1 - Х1У1               -cxrzr0

- ^1У1 ^i + Z^          cyrzr + SZ^!0

- cx_Yz_Ycy_Yz_Y + gz_Yw_Y (СУ1 + gw_{Y ) +(} CX-^ _{) +(} 3^i _{) 0}

00      00

]

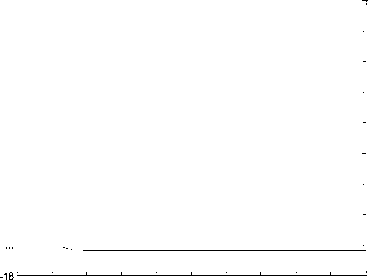
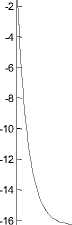
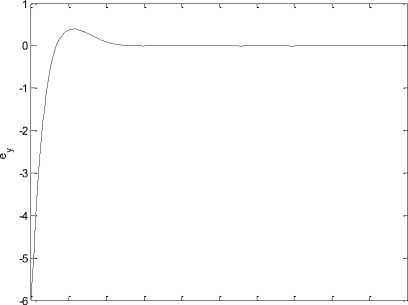
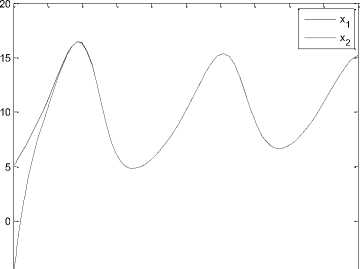
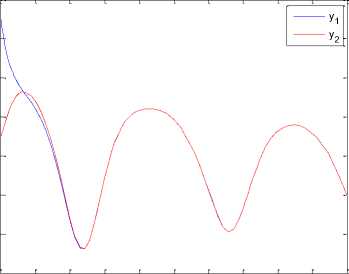
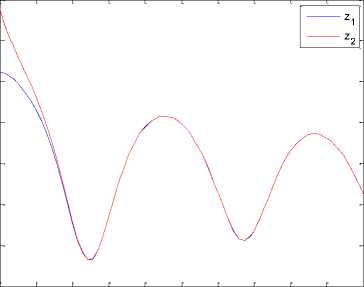
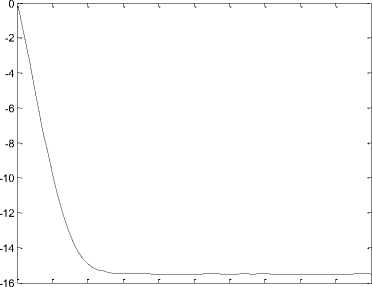
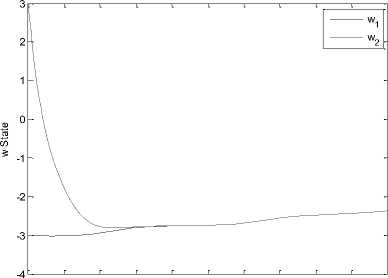
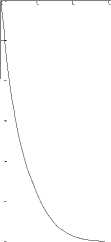
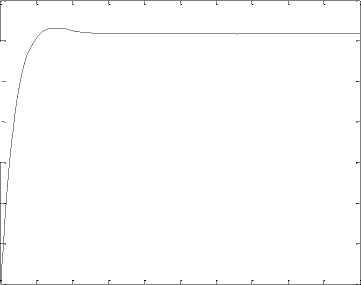
Again, the Riccati equation is solved and the optimal feedback control (6) is obtained. Synchronization errors e,ey,e,e in hyperchaotic system are shown in Fig 7. The time response of x,y,z,w states for drive system (16) and response system (17) is shown in Fig 8. The time response of the control inputs u2_,u2,u3,u4 for the synchronization of hyperchaotic system is shown in Fig 9.

-2

-6

-8

-10

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

-1

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9      1

Time(Sec)

Fig. 7.synchronization errors (e,ey,e,e ) in drive system (16) and response system (17).

-5

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

-2

-4

-6

-8

-10

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

-5

-10

-15

-20

-25

-30

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9      1

Time(Sec)

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9      1

Time(Sec)

Fig. 8.the time response of signals (x,y, z, w) for drive system (16) and response system (17).

-6

-1

-2

-3

-4

-5

-7

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

Fig. 9. the time response of the control inputs (u1,u2,u3,u4).

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

-0.2

-0.4

-0.6

-0.8

-1

-1.2

-1.4

-1.6

-1.8

c

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Time(Sec)

-2

VI. Conclusion

In this paper, stabilization and synchronization problem of the new hyperchaotic system was investigated. For this reason, state dependent Riccati equation (SDRE) was used. This method was applied to new hyperchaotic system in three ways. Stabilized system with know parameters, stabilized system with unknow parameters, sysnchronized system. In every way, simulations proved abilities of method.