Cooperative Spectrum Sensing and Weighted-Clustering Algorithm for Cognitive Radio Network

Published Online March 2011 in MECS

Wireless spectrum is a valuable and non-renewable resource. With the rapid development of the wireless communication, modern communication technologies have been presented consistently, which need to utilize new frequency bands that had been exhausted because of the static spectrum allocation policy. Studies from the Federal Communication Commission (FCC) show that the utilization of licensed spectrum only ranges from 15% to 85% [1]. Aimed at making full use of these idle spectrums, IEEE 802.22 Wireless Region Area Network (WRAN) Group is established to utilize the spectrum between 54MHz and 862MHz [2],[3]. As a very promising candidate for WRAN, cognitive Radio (CR) is considered as a potential solution to improve spectrum utilization via opportunistic spectrum accessing [4]. CR system is an intelligent wireless communication system that is aware of its surrounding environment and uses the method of understanding-by-building to learn from the environment and adapt its internal parameters in real-time [5].

In CR networks, the unauthorized user, called as Secondary User (SU), can use the licensed bands when the authorized user, namely Primary User (PU) is absent. For the SU, in order to utilize the frequency bands that not occupied by the PU, the SU should accurately identify the spectrum hole (white space). When spectrum hole is found through some kinds of detection technologies, it is reused to communicate. However, in order to protect the PU from interference, the SU has to get awareness and vacate immediately when the PU is active. So the spectrum sensing technology is the premise and the key technology to realize the CR.

There are two categories to identify the presence of the PU, the independent detection and the cooperative detection. In the independent detection, the final decision on the presence of PU is made by itself, such as energy detection, matched filter detection and cyclostationary feature detection [6].

• 1)    Matched filter detection

A matched filter is a optimal linear filter designed to maximize the Signal to Noise Ratio (SNR) for a given input signal. It is realized by coherent demodulation which needs the prior knowledge of authorized signal of PU, such as modulation pattern, wave-shape of impulse response and packet format. The main advantage of matched filter is that it needs less detection time to achieve high system gain due to coherent detection [7]. Another significant disadvantage of the matched filter is that it would require a prior knowledge of PU, which is usually unknown. Even the prior knowledge is known, but not accurate, the matched filter also performs poorly[8], [9].

• 2)    Cyclostationary feature detection

In a authorized network, in order to demodulate and decode the authorized signal, there are usually some redundant information which make the signal possess the cyclostationary periodicity, such as pilot, segment sync, field sync, or cyclostationarity. The idea of the cyclostationary feature detection is to utilize the built-in periodicity of the modulated signal [9]. The main advantage of this detection is that it can discriminate the noise energy from the modulated signal energy, especially at a very low SNR values. So cyclostationary feature detection is more robust to noise than energy detection. However, it requires long observation time and higher computationally complex [8], [9]. In addition, it also needs the prior knowledge of the authorized signal.

• 3)    Energy detection

Energy detection makes a decision about the existence of authorized signal based on the signal’s total energy by observing it within a observation space (time domain or frequency domain). The principle of energy detection will be discussed in section II. The performance of the energy detection is highly susceptible to fade and threshold value, especially noise uncertainty. Another challenging problem is that is has poor ability to differentiate the interference from other SU signals [8]. So compared with other two detection methods, energy detection is a sub-optimal detecting algorithm. Because it needn’t the prior knowledge of PU signal which is unknown actually, it is the most common detection method for spectrum sensing in cognitive radio network. Furthermore, energy detection has simple implementation, low computational complexity and good flexibility. Based on above consideration, we adopt energy detector to realize the spectrum sensing throughout this paper.

• 4)    Cooperative detection

Unfortunately, the sensing performance of independent detection will be degraded because of the fading, shadowing and hidden terminals. To enhance the detecting performance, the cooperative detection is proposed. In the cooperative detection, the local observed results come from different users in a CR network are shared each other. In a centralized CR network, the Fusion Center (FC) will collect the local observed results or local decisions come from different cooperative users and make a combined decision about the presence of the PU in the target licensed band. And in a decentralized CR network, i.e. Ad hoc, each cooperative user will make a final decision based on the shared data come from all users, because there doesn’t exist the FC.

However, conventional cooperative sensing isn’t efficient when users suffer different fading environments. So many present works focus on the weighted-cooperative. A weighted cooperative spectrum sensing scheme based on distance is proposed in [10], but it only takes care of the distance of different SUs. In [11], the weight factor is amplified according the contribution of the SU to the final decision, such as high probability of detection, high SNR, but it doesn’t give the computing formula of different weight factor.

In this paper, a novel weighted-clustering cooperative sensing algorithm is proposed. In each cluster, the weighting is about equal because of the closed distances to each other. But the weightings of the clusters are different because of the different fading environments between the clusters and the FC.

The rest of this paper is organized as follows. In Section II, the energy detection model in the local spectrum sensing is introduced. In Section III, we study the performance of conventional cooperative spectrum sensing in detail. In Section IV, the weighted-clustering cooperative spectrum sensing is demonstrated and analyzed. Simulation results are shown in Section V and conclusions are drawn in Section VI.

• II.    system model and local sensing

The energy detection accumulates the energy within a restraint band. If the accumulative energy is higher than the threshold, the PU is active, or, the PU isn’t present. Fig.1 depicts the block diagram of energy detection.

Fig.1 Block diagram of energy detection

First of all, the PU signal is amplified by the Radio Frequency Amplifier (RFA) before passing the Lower Passing Filter (LPF) and A/D converter. And then the detector measures the mean energy of input signals after being sampled and squared. Finally, the measured value will be compared with a threshold to determine whether the PU is active or not.

In fact, according to the digital signal processing, the system model of detection is under the test of the following two hypotheses:

У ( ⁿ ) =

u ( n )

s ( n ) + u ( n )

H 0

H 1

where y(n) is the signal received by SUs, s(n) is the transmitted signal by pu , and u(n) indicates the additive white Gaussian noise. Under H 0 , the received signal y(n) is only noise while under H 1 , y(n) consists of PU signal and noise. We make the following assumptions.

• •    S1) The noise u(n) is a real-valued Gaussian, independent and identically distributed (iiid) random process with mean zero and variance E [ ^{| u ( n} ) | 2 ] = ^ 2 ;

• •    S2) The primary signal s(n) is a real-valued and iid random process with mean zero and variance E [ ^{| s ( n )| 2} ] = ^ ²;

• •    S3) The PU signal s(n) is independent of the noise u(n).

The statistic value for energy detector is given by

M - 1        ²

Y = Й 21 У ( n )|              ⁽²⁾

^M n = 0

where M is the sampling number of received signal.

Under hypothesis H0, the test static Y is a random variable whose probability density function (PDF), namely p0 (x). If the detection threshold that we chosen is X , the probability of false alarm is then given by да

P_f ( X ,M ) = P r₆ „ (Y >  X | H 0 ) = £ p ₀( x ) dx (3) According to Central Limit Theorem (CLT), for a large N, the PDF of the static value Y under hypothesis H 0 can be approximated by a Gaussian distribution with mean M ₀ and variance o 0 given by

p да

P f ( X , M ) = P Re v ( Y > X\ H 0 ) = ^ _X p 0 ( x ) dx

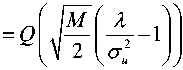
where Q ( • ) is the cumulative distribution function of the

standardized normal variable x . For a scalar x , Q ( x ) is

given by

M 0 = 0 2

^o 0 = M ^{[ E} I u ⁽ n ) I ⁴ —° ⁴ ]

1 _Гда — t-

Q ( x ) = — [ e ² dt

<2n Jx

For a real-valued Gaussian variable

E | и ( n ) |⁴ = So 4 , so

(T_n² = — [ S o ⁴ — О ⁴ ] = — О⁴

⁰ M ^{L 4   4 ]} M ⁴

u(n),

If the PU is active, according to (9), the PDF of Y is given by

^{[ x — (} Y + 1) ^o 4 ² ]

1                  T4 ( Y + 1) 2 o ₄ ⁴

P 1 ( x ) =-----i=--------- e ^M (13)

V2 ^П_х ^--⁽Y + ^{1) o}4²

M

Under the hypothesis H1, we denote p1 (x) as the PDF of the test static value Y. For a given threshold X , the probability of detection is given by да

P d ( X , M ) = P Rev ( Y >  X I H 1 ) = £ P 1 ( x ) dx    (6)

For a large N, the PDF of the static value Y can be approximated by a Gaussian distribution with mean 2

M and variance О" 1 given by

M i = ^{y +} 1 V 2

According to (6), the probability of detection is да

P d ( X , M ) = P Re v ( Y > X I H 1 ) = J P 1 ( x ) dx

J X

= Q

<

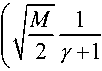
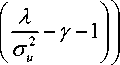
0 -12 = -1 ^[ E I s ⁽ n ) I⁴ + E I ^{4 (} n ^)|4 (a ^{— o} 0 ^{)2 ]} 1 M              su

For a real-valued Gaussian variable s(n) that irrelevant with u(n), E | s(n) |4 = Sos4, thus

О ² = ± [ S o ² + 3 ° ² - ( _CTs ² - ° ² ) ² ] = A y + 1) 2 o ⁴

1     s usu        u

1 M s usu M u

is

For a target probability of false alarm, P _f , eliminating the parameter of threshold X according to (11) and (14), the probability of detection is given by

Pd = Q f    fQ"‘(P)—YM '1'1

V Y +11

On the other hand, for a target probability of detection, P _d , the probability of false alarm is also related to the target probability of detection as follows.

Pf = Q f (y+1) Q 4( Pd) + Y^M '

° 2 where y is the Signal Noise Ratio (SNR), y = —^s— .

° u

So the static value Y under the hypotheses H 0 and H 1 are approximated by Gaussian distribution as follows.

Y ~ <

N ( o² , — o ⁴)

^u , M ^u                         (9)

^{N ((} Y ^{+ 1) o} u² , "^(.Y ^{+ 1)2 o4}u )

where N ( • , • ) is the normal distribution function. Then under hypothesis H 0 , the PDF of Y is

P 0⁽ x ) =

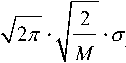
e

u

( x - £ м 2)2

4 4 M ° ⁴

According to (3), the probability of false alarm is

III.    Conventional Cooperative sensing

In cooperative spectrum sensing, each SU observes the PU signal and then forward the observed result to the FC. The decision made in the FC can be taken in two ways – one is based on the observed results of the SUs, namely soft combination and the other considers only the final one bit decision from each PU, namely hard combination.

A. Data Combination Methed

In hard combination method, each SU make local decision based on its observed values compared with the chosen threshold, and then forward the local decision, denoted D i e {0,1}, to the FC to identify the PU is present or not. There are usually three combination method based on the decisions come from different cooperative users, such as OR rule, AND rule and K-out-of-N rule.

For OR rule, if there just one SU to identify that the PU is active, the FC will declare the PU active. Thus the cooperative probability of detection Qd and probability of false alarm Qf are given as follows.

N

Q d = 1 - П (1 — P d , - -)

N

Qf = ¹ — П (1 — f)

where P _{d , i} and P _{f , i} are the i th SU local probability of detection and probability of false alarm, N is the number of cooperative users.

Assume each SU achieves identical P _d and P _f in the local spectrum sensing (i.e., P d = P d i and P f = P f i , V i = 1, 2, l , N ). The cooperative probability of detection and probability of false alarm are the given by

Q d = 1 - ( 1 - P d ) N

N

Q . = ¹ - ( 1 — P f )

Note that the cooperative missing probability is

Q m = 1 - Q d = ( 1 - P d ) " = ( P m ) "

where P _m is the missing probability of local sensing user.

AND rule is just opposite to OR rule, in which the FC will declare the PU active only when all cooperative users identify that the PU is present. Q d and Q f under AND rule are written as follows.

Q d = ( P d ) N

N

K-out-of-N rule is a tradeoff between OR rule and AND rule. In this rule, when more than K users show that the PU is active, the final decision of cooperative sensing is that the channel is occupied. So under K-out-of-N rule , the Q d and Q f are given by

N

Q d = Z [ C N ( P d ) i (1 - P d ) N " i ]

i = K                                  (21)

N

Q f = E [ C N ( P f ) ' (1 - P f ) N - ' ]

i = K

B.    Performance of Cooperative Spectrum Sensing

• 1)    Independent detection versus cooperative detection

  In Fig.2, we analysis the sensing performance under the target probability of false alarm under the simulation environments with SNR= -15dB and sampling number M=1024. As show in Fig.2, the cooperative probability of detection with OR rule is highest than any other method. However, the cooperative sensing performance with

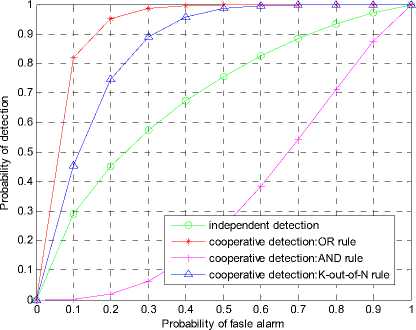
Fig.2 Spectrum sensing performance with the target probability of false alarm

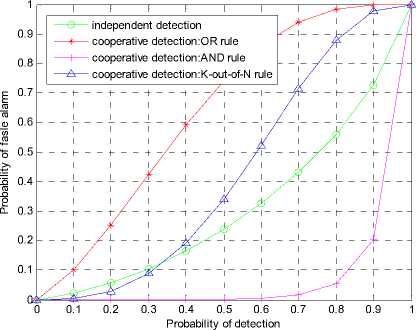
Fig. 3 Spectrum sensing performance with the target probability of detection

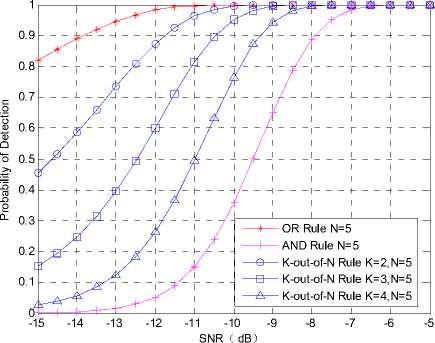
Fig.4 Cooperative spectrum sensing performance with various rules

AND rule or K-out-of-N rule is worse than the sensing performance under independent detection. So from the perspective of SU, the OR rule improve the utilization of cognitive radio network. Fig. 3 depicts ROC curves under the target probability of detection, in which the AND rule of cooperative sensing has the lowest probability of false alarm. On the contrary, the probability of false alarm with

OR rule is worst than others. This shows that AND rule focuses on the protection to the authorized user.

• 2)    Cooperative performance with various rules

  Fig.4 shows the ROC curves of different combination rules under different SNR. We assume the sampling number M=1024 and the probability of false alarm P f =0.1. As shown in figure, for a target probability of false alarm, the probability of detection of OR rule is much higher than AND rule and K-out-of-N rule, especially under the lower SNR, i.e., -10dB. For example, with SNR=-13dB, the probability of detection for OR rule is 94.7%, while that for AND rule is 1.7%.

• 3)    Observation time of signal

  In energy detection, we should transform the analog values into digital values with some methods, i.e. fast Fourier transform (FFT). Specifically, the received signal is sampled in a time window. When the signal is observed, the time and the sampling frequency is fixed, namely, the sampling number M is constant. The complementary ROC curves in Fig.5 indicate the sensing performance with different observation time under the OR rule. It is evident from the curve that, with same SNR, the CR network performs better detection accuracy under longer observation time. For example, when M=2048 and SNR=-15dB, the improvement is about 19.78% compared with M=512.

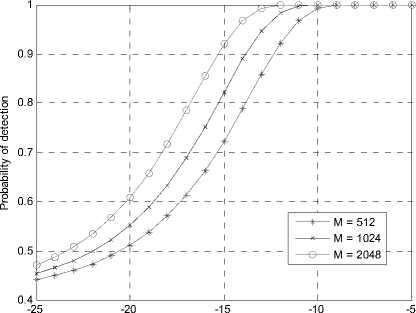
SNR ( dB )

Fig. 5 Cooperative spectrum sensing performance with different sampling numbers

• 4)    Numbers of users

As show in Fig.6, for cooperative spectrum sensing, the numbers of cooperative users will affect the system performance. The probability of detection presented in Fig.6 clearly depicts that the idle spectrum is better utilized in more cooperative users, for a given probability of false alarm, i.e. P f =0.1, it achieves higher probability of detection with the same SNR which, in turns, means that CR network has larger throughput.

But the performance of CR network is much better with the increasing numbers of cooperative users. We denote that the probability of error of CR network is

Q e = Q f + Q m               (22)

In Fig.7, we simulate the performance of CR network under the environment with SNR=-15dB and M=1024. It is evident from Fig.7 that, the probability of error is decreasing with the increasing numbers of cooperative users which, in other word, the performance of CR network is improved. But when the numbers of cooperative users is large enough, especially N>15, the probability of error is up to a limitation.

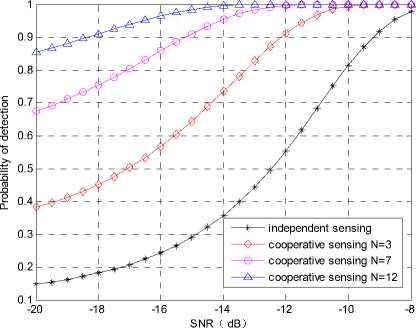
Fig. 6 Cooperative spectrum sensing performance with different numbers of users

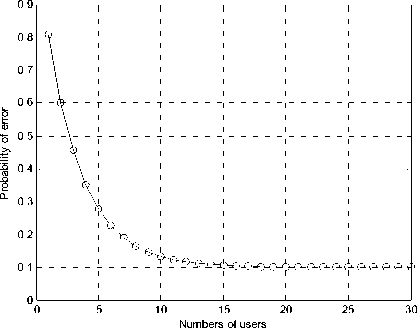
Fig. 7 Probability of error with different numbers of users

• IV. Cooperative sensing with proposed method

In conventional cooperative spectrum sensing, all cooperative users have the same contribution to finally decision. But in factual environment, each SU will experience different fading environments and different distances to PU. In this paper, we propose a weighted-cooperative sensing scheme using clustering, which assigns different weightings to different clusters to enhance the performance of the cooperative spectrum sensing effectively and impartially.

A.    Clustering Scheme

In a factual CR networks, the location of SU is randomly distributed. Therefore, some SUs may suffer deep fading while others may not. On the other hand, some users may locate near to each other, which experience the same path fading and is supposed to have the same SNR. So in this paper, we adopt clustering scheme according to some existent methods.

The CR network structure based on clustering method is illustrated in Fig.8. All SUs are assumed to be separated into several clusters by some clustering methods. And in each cluster, a cluster-head is selected to report the cluster-decision to the FC according to some rules. In [12], a Low Energy Adaptive Clustering Hierarchy (LEACH) is proposed, in which a pre-elector cluster-head will broadcasts its energy, if there no any other node’s energy is bigger than its own energy, then it is the finally selected cluster-head of this cluster. [13] is similar with [12], in which the base station broadcasts all node’s energy, and then each node sets a time to start advertising itself to form clusters based on the broadcasting information. In order to resolve the energy consumption problem associated with the repetitive setup, [14] proposes a Routed-Robin Cluster Header (RRCH) method that fixes the cluster and selects the head in a round-robin method. In [15], in addition to energy consumption, load balancing and network’s scalability have been taken into account. These clustering methods can solve the critical problem in conventional cooperative spectrum sensing, which also mean that the clustering concept is available to improve the detecting performance.

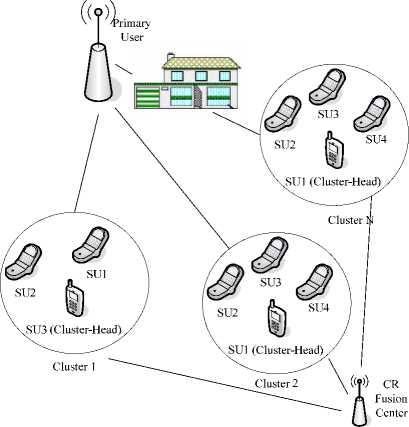
Fig. 8 Cluster-based cooperative spectrum sensing

B.    Weighted-Clustering Cooperative Spectrum Sensing

In order to improve the detecting performance, we propose a novel weighted-cooperative spectrum sensing algorithm using clustering.

Firstly, all SUs are assumed to have been separated into a few clusters according to a kind of method. Subsequently, the cooperative spectrum is conducted as the following steps:

• •    1) Every SU j in cluster i collects the energy E _{i , j} and sends a local observation B _{i , j} to the cluster-head, where B _{i , j} is related to E _{i , j} by a function Ω

B i , j =Ω ( E i , j )                    (23)

• •    2) The cluster-head receives those local observations in the same cluster and then make a cluster-decision C _i according to some data fusion function Φ considering the weight factor α i , j

C i ^=Φ ( α i ,1 B i ,1 , α i ,2 B i ,2 , ^L , α i , Ni B i , Ni )

In (24), α _{i , j} is the weight factor for the SU j in cluster i , i = 1,2, L K , j = 1,2, L N _i , where K is the number of clusters , N i is the number of secondary users in the i th cluster. In this paper, the cluster-decision result is based on hard combination, which is insisted of {0, 1}.

• •    3) The cluster-decision C _i for all i are reported to the FC to determine a final decision F according to a fusion function Ψ , as

F = Ψ ( β 1 C 1 , β 2 C 2 , L , β K C K )        (25)

where β _i , i = 1,2, L , K , is the weight factor of cluster i .

We assume that the channel condition between SU and cluster-head in each cluster is perfect because of the closed distance to each other. Thus in the same cluster, the difference of weight factor α _{i , j} is nearly ignored, i.e. α _{i , j} = α _i , ∀ j = 1,2, L , N _i , even α _{i , j} = 1 . But the weight factor β _i of cluster i should not be ignored because of the long distance between clusters and the FC. The closer to the FC the bigger weight factor, then the information with higher weight factor has greater contribution to the final decision. Conversely, the farther to the FC the smaller weight factor, then it has lower factor on the final decision, even it is not reliable, has no affection to the final result. Thus the weight factor β _i is given by

βi= LiG(26)

subject to

K

∑βi=1

• i = 1

L _i is the average distance coefficient of cluster i :

Ni

Li= ∑(1 di,j)

j = 1

where d is the distance between the SU j in cluster i i,j and the FC. And G is the normalized coefficient of all Li:

KKNi

G = ∑ L i = ∑∑ (1/ d i , j )        (29)

• i = 1 i = 1 j = 1

The FC makes the final decision that the PU is active based on different values Ci according to K-out-of N rules, in which K out of N cooperative clusters of CR network declare the presence of PU. And the decision

rules are written as	follows. K
	£ P i C i >  n	H 1
	i = 1 £ e c < n	H 0	(30)

. i = 1

where the decision parameter n is chosen according to the factual environment. And the probability of detection Q _{d _ c} and probability of false alarm Q _{f _ c} in our proposed method can be expressed as:

£ дс,> n\H(3i) i=1

K

Qf c = p^£Ж>n\Hо[

I /=1

• V.    simulation results

  In this section, we provide simulation results to validate the performance gain of our proposed method. In our simulation, we assume that there are 4 users in each cluster and there are 3 clusters in the CR network. The observed signal is sampled with the sampling numbers N=1024. For comparison, the conventional cooperative spectrum sensing methods, i.e. AND rule and K-out-of-N rule, and the weighted-cooperative sensing are also simulated.

Probability of false alarm

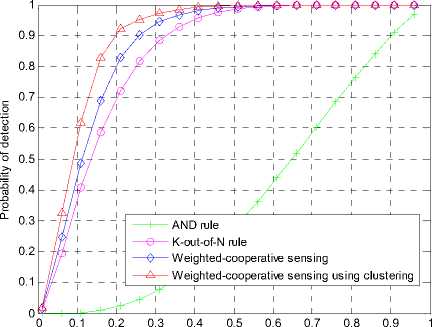
Fig. 9 ROC curves of different cooperative schemes

Fig.9 shows the ROC curves of different cooperative schemes. AND rule has the worst performance among all the combination schemes because AND rule’s target is to minimize the probability of false alarm. It can be observed that, under the same probability of false alarm, the probability of detection of the weighted-cooperative sensing scheme using clustering is obviously improved compared with the other three cooperative methods.

In Fig.10, we simulate the average probability of error, which is the sum of average probability of missing and probability of false alarm, vs. local sensing SNR curves with the target probability of detectionPd = 0.9 . If AND rule is used in cooperative spectrum sensing, the system can not work under lower SNR, i.e. SNR <-10dB. Our proposed scheme shows better performance than the other three cooperative methods, whose average probability of error is very low.

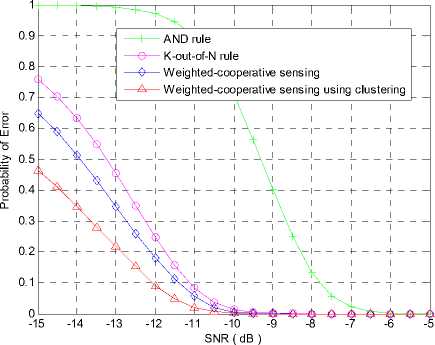
Fig.10 Error probability vs. average SNR of different cooperative schemes

• VI.    conclusions

In this paper, we study the performance of cooperative spectrum sensing which is related to combination rule, observation time, and number of cooperative users. For SU, the OR rule could achieve higher spectrum utilization while AND rule could protect the PU better from interference. With the increase in the numbers of cooperative and time of observation, the CR network performs better. However, the performance of CR network will not be improved as the number of cooperative users is up to a certain amount. So there is a tradeoff between the system performance and numbers of cooperative users. In previous works, some weighted cooperative spectrum sensing methods are proposed. In this paper, different from them, we proposed a novel cooperative spectrum sensing algorithm, in which the distances and clusters are both considered. In cooperative spectrum sensing, we assume SUs have been separated into several clusters, at the same time, consider clusters’ contribution to the final decision, namely weight factor. Simulation results and analysis show that the proposed spectrum sensing scheme can achieve better performance and lower error probability.