Cooperative spectrum sensing based on softened two-bit hard combination scheme

Cognitive radio(CR) is a new paradigm in wireless communications that promises an enhanced utilization of the limited spectral resource. The basic idea is to employ a hierarchical model, where primary (licensed) and secondary (unlicensed) users coexist in the same frequency spectrum. The cognitive radio system include several functions, the important function is spectrum sensing which detects the unused channel. There are number of schemes for spectrum sensing like energy detection, matched filter detection, and cyclostationary detection. One of the great challenges of implementing any spectrum sensing is the hidden terminal problem. This occurs when the CR is shadowed, or degraded with high path loss while the primary user(PU) is still in operation. Cooperative spectrum sensing was proposed to overcome noise uncertainties, fading and shadowing in PU signal detection. It can be as a solution to hidden node problem and decrease sensing time as well. In this technique, CR users/ nodes are collaborated to sense spectrum hole and detect PUs signal. Several works[1–8] have shown that cooperative spectrum sensing can greatly increase the probability of detection in fading channels

It can be seen that cooperative spectrum sensing will go through two successive channels: (1) sensing channel (from the PU to cognitive radios); and (2) reporting channel (from the cognitive radios to the common receiver). Cooperative spectrum sensing can be implemented in three models, centralized sensing, distributed sensing, and relay-assisted sensing. In centralized sensing, sensing information of individual users will be collected in a central unit. The central unit decides the spectrum availability and broadcast this information to the other users. In distributed spectrum sensing, CRs share sensing information among each other and the decision is made individually. In relay-assisted cooperative sensing, since both sensing channel and report channel are not perfect, a CR user observing a weak sensing channel and a strong report channel and a CR user with a strong sensing channel and a weak report channel, for example, can complement and cooperate with each other to improve the performance of cooperative sensing.

• I.    System model and data fusion

A-System Model

Consider a cognitive radio network, with K cognitive users (indexed by k = {1, 2. . . K}) and a common receiver, as shown in Fig.1. The common receiver is introduced as a BS which manages the cognitive radio network and all associated K cognitive radios. Each cognitive radio performs local spectrum sensing independently. Before the CRs use the licensed spectrum, itshould detect whether the PU is present or not by using any method of spectrum sensing. When a CRs is sensing the spectrum channel of the PU in the cognitive radio network, there are two hypotheses for the received signal X(n) : absent or present, which are denoted by H 0 and H 1 respectively. Then,

HMn) = WM

^■ХМ = hks(n) + Wk(n)

Where s(n) are samples of the transmitted signal (PU signal), W k (n) is the receiver noise for the k^th CR user that is additive white Gaussian noise (AWGN), and h _k , is the complex channel gain of the sensing channel between the PU and the k^th cognitive radio.

The local detector (energy detector(ED)) decides whether the signal exists according to the signals that are received, and sent to the center their decisions upon which the center makes the final decision. The observed energy at the k^th CR user is given by

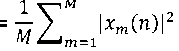
Where M denotes number of collected samples.

Let λ be the local decision threshold for each CR user, then the local false alarm probability, which defines the probability of the algorithm falsely declaring the presence of primary signal ( P f _{, k} ) under hypothesis H 0 , can be obtained from (3) as

г

Pf = Pr{Decision = Hr\H0} = Pr[E(x) > X\H0} = -

M A

Where Г(..) and Г(..,..) are complete and incomplete gamma function respectively.

The detection probability, which defines the probability of the algorithm correctly detecting the presence of primary signal ( P_d ) under hypothesis H ₁, is given by

P_d = Pr{Decision = H^HJ = Pr{E(x) > ЗД} = Q_M/2(^ VI)

1     ( Y

fM =техр --

Where γ is the average SNR. The average P_d in this case, P_{d, Ray} is given as:

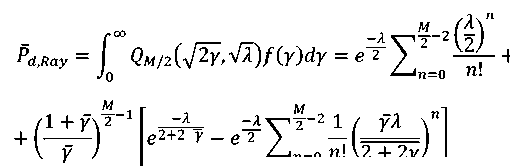
B-Data Fusion

In cooperative sensing, data fusion is a process of combining local sensing data for hypothesis testing, which is also an element of cooperative sensing. Depending on the control channel bandwidth requirement, reported sensing results may be of different forms, types, and sizes. In general, the sensing results reported to the fusion center (FC) or shared with neighboring users can be combined in three different ways in descending order of demanding control channel bandwidth:

• (i)    Soft Combining: CR users can transmit the entire local sensing samples or the complete local test statistics for soft decision.

• (ii)    Hard Combining: CR users make a local decision and transmit the one-bit decision for hard combining.

• (iii)    Quantized Soft Combining: CR users can quantize the local sensing results and send only the quantized data for soft combining to alleviate control channel communication overhead.

Obviously, using soft combining at the FC can achieve the best detection performance among all three at the cost of control channel overhead while the quantized soft combining and hard combining require much less control channel bandwidth with possibly degraded performance due to the loss of information from quantization. In this paper, only quantized soft combining scheme in centralized sensing is considered which is described below in details.

B-1 Quantized Soft Combining in Centralized Sensing

In order to make a tradeoff between the overhead and the detection performance, instead of one bit hard combining, where there is only one threshold dividing the whole range of the detected energy into two regions, a better detection performance can be obtained if the number of threshold is increased to get more regions of observed energy. In this paper, only two thresholds are considered leading to softened two-bit hard combination scheme.

In softened two-bit hard combination scheme, each user divides the whole range of its measurement, such as the received signal energy within a predetermined interval, into R regions and reports to the combining node which region has its observation that falls in. Therefore R is the number of distinctly quantized sensing results from each user. When R = 1, the sensing information from each user reduces to one-bit hard decision on the absence or presence of the licensed signal; if R goes to infinity, the sensing information of each user becomes its original measurement. As shown in Fig.2, softened two-bit hard combination scheme differs from the conventional one-bit scheme with only one threshold, three thresholds in the two-bit scheme λ 1 , λ 2 and λ 3 divide the whole range of observed energy value into 4 regions. Each CR user needs to exchange twobits information on their observed energy values. The primary signal will be declared present if any one ofthe observed energies falls in region 3, or L ones of them fallin region 2, or L² ones fall in region1, where L is a designparameter to be optimized.

In other words each region is allocated an integer weight: w 0 = 0, w 1 = 1, w 2 = L and w 3 = L^2. The weighted summation N_c is given by:

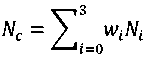
Where N_i is the number of observed energy values falling in the i th region. Then N_c is compared with the threshold N T = L². If N c ≥ N T , primary signal is declared present; otherwise, it is declared absent.

For the two-bit hard combination scheme, thresholds λ1, λ2, and λ3 need to be determined to meet the target overall false alarm probability of the K-user CR network Qf, exactly, and also to optimize the detection performance. Suppose theprimary signal is currently absent. To avoid false alarm, theremust – 1121 – be no CR user in region 3. Assume there are j users in region 2, i – j users in region 1, and all of the rest

K – i users fall in region 0, i.e., N3 =0, N2 = j, N1 = i – j, and N0 = K – i. Then the weighted summation, Nc =(i – j)w1 + jw2, needs to be less than L2 so as to avoid false alarm. As a result, it is required that i ≤

L2–1 and

j < min

L2 — 1 — iwr

W2 — wr

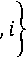
Where [■ J denotes the largest integer no greater than the argument.

The false alarm probability Q f , and detection probability Q _d , of the softened two- bit hard combination scheme in case perfect reporting channel are given by:

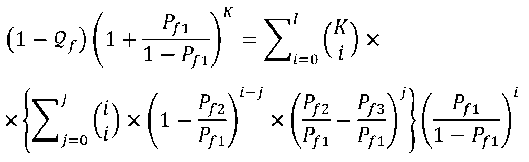
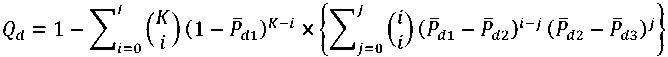
Where P d1 , P d2 , and P d3 , denote the average local detection probabilities under fading channels, corresponding to thresholds λ 1 , λ 2 and λ 3 respectively.

• II.    Simulation results

The system model shown in Fig. 1 is investigated by computer simulation over Rayleigh fading channel and AWGN. The energy detection is used as spectrum sensing technique. The performance of the system is measured using complementary receiver operating characteristic(ROC) curves. The ROC has been widely employed in signal detection theory due to the fact that it is an ideal technique to measure the trade-off between the probability of detection and the probability of the false alarm. The performances of the system with softened two-bit hard combination scheme for multiuser are measured. Two measures are considered including effect of false alarm probability, and effect of the number of users. Also, comparison between softened two-bit hard decision scheme and one-bit hard decision scheme is considered.

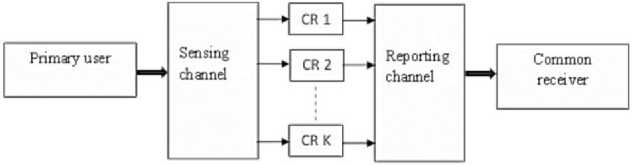
Fig. 1. System model

	Energy
Region 3 (w3)
Region 2 (w2)
Region 1 (wi)		^-i
Region 0 (w0)

A-Effect of False Alarm Probability

The Q _d is evaluated with respect to average SNR considering two values of Q f , 0.05, and 0.2. The number of samples is fixed at M=6, and K=4.

Fig.3 show the performance of the system. It can be observed that Q _d increases when SNR or Q f increases

Fig. 2. Principle of two-bit hard combination scheme

B-Effect of Number of Users

Fig.4 show the Q _d versus SNR for different number of CR users, K=1,4,6, while, Q f =0.2 and M=6. It can be concluded that as K increases, the Q _d increases. Also, Q _d increases with the increase of SNR.

C–Comparison Between Softened Two-Bit and One-Bit hard decision schemes

Fig.5 shows Q _d versus SNR for one-bit and softened two-bit hard decision combination schemes, when M=6, K=4, and Q f =0.2. It can be concluded that Q _d for two-bit scheme is better than that for one-bit scheme.

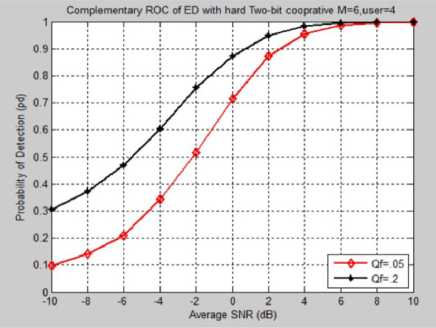
Fig. 3. Q d versus average SNR for different Q f

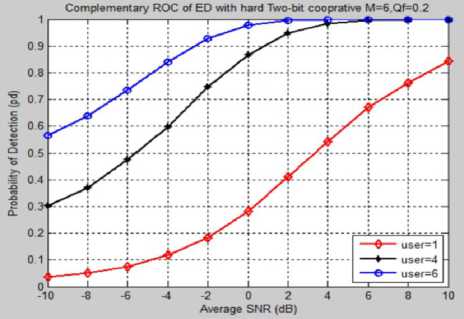
Fig. 4. Q d versus average SNR for different K

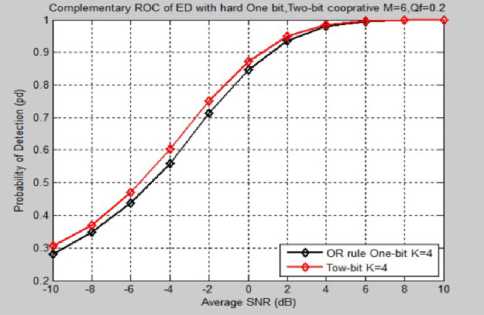
Fig. 5. Q d versus average SNR for one-bit and two-bit schemes

Conclusion

Cognitive radio is a novel technology that can potentially improve the utilization efficiency of the radio spectrum. The performance of cooperative spectrum sensing in CR over Raleigh fading channel and AWGN was studied. The performances with softened two-bit hard combination scheme are measured using energy detection technique. The results show that Q _d increases with the increase Q f , K, and SNR.