COVID-19 epidemic modeling - advantages of an agent-based approach

The system of making important management decisions requires the usage of specially developed software which makes it possible to model the real socio-economic situation, predict its development, and pre-evaluate the consequences of certain planned measures. In the context of the COVID-19 pandemic, managers at various levels have to quickly make unprecedented decisions, which makes the availability of such model tools even more relevant, since it allows accumulating and analyzing the “virtual” experience of efficient and inefficient decisions obtained during model (computer) experiments. This experience can be used in the future when similar situations occur, that is, it will help quickly make better prepared decisions in the event of a new epidemic caused by a similar or any other infection.

Epidemics’ spread is a well-studied and well-formalized process, which makes it possible to model it. The main model of epidemics is the model developed by Anderson G. McKendrick and William O. Kermack. It describes the spread of infection transmitted from person to person [1]. The entire population, according to their concept, is divided into groups depending on the status in relation to a studied infection. In the basic SIR model, these groups are: S – Susceptible (those who do not have immunity and can be infected), I – Infectious (infected and infectious), R – Recovered (recovered and acquired immunity), which corresponds to the main stages of the disease. Over time, as the infection spreads, the status of individuals may change, which means that they move to another group. The sequence of letters in the abbreviation of SIR means the sequence of people’s moving from one group to another. The basic SIR model was becoming more complex as time passed, new stages of a disease (and related groups) were added to it, which allowed taking into account the propagation characteristics of various types of infections in more details. There appeared such modifications of the SIR model: SIS – for infections that do not form a stable immune system (for example, seasonal flu); SEIR – for infections with an incubation period (which includes the COVID-19 virus), and others. In addition, for all these modifications of the basic model, there are options with adding D at the end – death stage for a separate account of the dynamics of the deceased.

Based on the SIR class models, a field of epidemic modeling has developed, which has experience in successful practical developments using various technological approaches.

Traditionally, to describe the dynamics of the epidemic, differential equations were used, for which the coefficients were selected characterizing the proper infection – its contagiousness, duration of the incubation period, lethality, etc. – and specific conditions for its spread – population size, initial number of infected people, presence/absence of immunity among population, etc. It is important that the usage of differential equations implies population’s homogeneity in terms of its participation in the spread of the epidemic. Therefore, in order to account for the heterogeneity existing in reality, conscientious researchers divide the population into groups (e.g. by age) and/or select the indicators characterizing, for example, the proportion of the infectious people among the infected ones or the starting point of the epidemic, achieving coincidence of the results of the model calculations with the observed real data. Only then they do move on to predictive calculations. M.V. Tamm’s work1 is a good example of such kind of a research, where the author used the COVID-19 Scenarios model2 [2], created under the supervision of Richard Neher, for calculations. It is also significant in another respect – the author emphasizes that data on detected infected people do not reflect the true picture of the infection spread and offers his own way of solving this problem.

Another approach to implementing the epidemic model is also possible: it is modeling from the point of view of an individual who is susceptible to infection and can move from one stage of the disease to another with a probability that depends on many factors. The most flexible method that implements modeling at the level of individuals is a special type of simulation – an agent-based one. The agent-based model (ABM) simulates the behavior of individual agents who are able to act independently in accordance with their interests and/or under the influence of the external environment, including under the influence of other agents. Main advantages of the agent-based approach, which has been commonly used in recent years for solving the problem of modeling epidemics, are:

• •    ejection from the requirement of knowledge about interdependencies of various global characteristics, since, in case of the agent-based model, change of a state of society as a whole (artificial society) is obtained as the result of aggregation of changes of individual members’ (agents’) state. As a result, it is possible to rely on more reliable information about processes at the micro level, that is, to describe the conditions for the agents’ transition from one stage of the disease to another, based on the experience of experts-practitioners involved in the patients’ examination and treatment;

• •    ability to reproduce an actual population structure on a population of agents based on characteristics associated with their sensitivity to the infection, and with their participation in the spread of the disease; in other words, to naturally take into account population’s heterogeneity and create the most realistic simulation of the epidemic.

A number of studies on ABM epidemics has become so great recently, that it has even led to the emergence of works suggesting their classification system. For example, there are four main groups of epidemiological ABM components: features of the disease and its spread; recreating society’s characteristics; simulating everyday movements of the population or social contacts; characteristics of the terrain and natural environment (climate, etc.) [3]. All models are conditionally divided into those that study the nature and dynamics of the epidemic spread in order to predict the epidemiological situation, and those that are designed to test measures to combat epidemics. A separate group includes those models that assess the cost-effectiveness of anti-epidemic measures, such as vaccination.

Let us show some examples of successful epidemiological ABM based on the transition of agents from one stage of the disease, corresponding to the scheme of the SEIR model, to another. Simulating the infection spread is based on individual agents’ social interactions. The models use geographic information systems (GIS) to visualize the epidemics spread on the map, resulting from modeling. These include the following works:

• •    a model of the spread of a measles outbreak in Burnaby, Canada [4], designed to study spatial diffusion of infectious diseases in an urban environment through a network of human contacts;

• •    a model of the 2009 H1N1 flu outbreak in Mexico [5], designed to assess the impact of government measures to restrict citizens’ mobility through official passes;

• •    a pandemic model in the Greater Toronto Area of Ontario, Canada [6], which takes into account individual levels of agents’ exposure to infection and their ability to transmit the disease, correlated with real demographic data and population behavior. The model is used by the Ontario Agency for Health Protection and Promotion as a tool for defining a strategy for mitigating the pandemic effects.

A classic example of a very large ABM that was created to solve an applied problem is Joshua Epstein’s full-scale distributed agent model of epidemics [7]. Initially, it included 300 million agents moving around the US map according to a 4000 x 4000 correspondence matrix, then expanded to 6.5 billion agents to simulate the effects of the influenza A (H1N1/09) virus spread across the entire planet.

There are also works that use different approaches. For example, two simulations – a system-dynamic and an agent-based one are compared using flu propagation models [8]; the results obtained using stochastic ABM and a structured metapopulation stochastic model for modeling the baseline scenario of a pandemic in Italy are compared [9]. The sociodemographic structure of the Italian population is reproduced in detail on the population of agents in the ABM. The global metapopulation model used data from censuses around the world, as well as data on airline travel flows with charts of people’s mobility. Both models were synchronized in their initial conditions, including parameters of a disease and a volume of infected people coming from international trips.

Special attention should be paid to the models developed for the current COVID-19 pandemic directly. First, we should note the classic example of using the SEIR class model [10] to simulate and analyze the COVID-19 outbreak in Wuhan, taking into account individual behavioral responses of people and government actions (holiday extension, travel restrictions, hospital deployment, and quarantine). The paper compares it with the 1918 flu pandemic in London.

In general, there is already a lot of research on the COVID-19 pandemic. It is sufficient to point to the portal MedRxiv. The Preprint Server for Health Science3, dedicated to the study of the most diverse aspects of the SARS-CoV-2 coronavirus pandemic, which hosts almost four and a half thousand scientific preprints, and most of them contain various types of epidemiological models. A wide variety of approaches are presented here, for example:

The econometric model [11] that evaluates the parameters of time series of data on COVID-19 mortality for such countries as South Korea, Italy, Spain, France, the United Kingdom, Germany, and the United States.

The global macroeconomic model Global VAR (GVAR) [12], which considers social interactions of people from different countries (Facebook data were used) and the impact of these interactions on the assessment of risks associated with the COVID-19 epidemic. The attitude to risks provides the basis for people’s behavior in an epidemic situation, their compliance or non-compliance with social distancing (aggregated indicators of mobility tracking obtained from Google Mobility Reports were used). The model also tracks the impact of the epidemic on important components of the economy, such as the labor market and unemployment.

The models of the SIR class . The model [13], in which the Greek population is divided into two groups, those younger and older than 40. It is investigated how the weakening of isolation measures separately for a particular group affects overall mortality rates. The model [14], which was experimented with using data from nine European countries, revealed pandemic characteristics that are invariant in different countries. The model also revealed a minor impact of average temperature in the country on the likelihood of infection in each contact, and higher temperatures are usually associated with lower infectivity.

The agent model [15] for assessing the impact of social distancing on the mitigation of the epidemiological situation.

However, the authors were most interested in cases of epidemic models that: a) use population differentiation by susceptibility to infection; b) explicitly take into account the characteristics of the infection itself; c) provide an opportunity to assess the impact of the epidemic on the health system; d) have an interface allowing to test various measures to counter the epidemic spread, since these components are considered by the authors to be key in creating an adequate simulation of the epidemic with the possibility of its further practical usage as a tool of supporting management decisions. From this point of view, the following works were the most important for us:

• •    a combined model of cholera spread [16] using differential equations that take into account the epidemiological characteristics of this disease in detail, as well as the mechanism of cellular automata to simulate people’s (agents’) ability to move;

• •    Richard Neher’s COVID-19 Scenarios model⁴ based on the usage of differential equations, which allows differentiating population groups by their susceptibility to infection and intensity of social contacts, depending on age, and varying the characteristics of the infection. The model is configured to assess the need for hospitalization, including resuscitation;

• •    ABM, developed by American and Indian scientists [17], which takes into account the differentiation of population by health level, economic status, and access to medical care, and uses data on actual prevalence of serious chronic diseases among population of different age cohorts. The model is designed to evaluate various vaccination strategies in terms of the achieved reduction in morbidity, as well as the financial burden of costs incurred. Cost efficiency is estimated by their correlation with the cost of disability that was prevented;

• •    ABM of H1N1 pandemic influenza in Egypt [18], developed by Egyptian scientists. Agents in the model are differentiated by age and social roles (including the intra-family ones), which is used to simulate their interaction and infection. The parameters that characterize the proper infection are set.

In addition, the model allows evaluating the efficiency of various measures to combat the epidemic spread.

The purpose of the present research is to develop ABM as a tool for predicting epidemiological dynamics depending on quarantine measures which would assess the peak loads on the health system based on a plausible simulation of the processes of individuals’ infection and their passing through the stages of COVID-19 disease.

ABM of the COVID-19 epidemic in Moscow

Problem statement

The COVID-19 infection itself is new and insufficiently studied, so the information about its epidemiological characteristics, the features of infection, the duration of various periods, etc. has been largely contradictory since the beginning of the epidemic. As of today, we can say the following with confidence:

• •    the infection is new; no one is immune to it;

• •    the infection is transmitted from person to person; face-to-face contacts between infected play a huge role;

• •    there is a fairly long incubation period from a moment of a person’s infection up to the disease; this period passes unnoticed for a person and others;

• •    during the incubation period, a person is a source of infection through face-to-face contact, that is, the latent period nearly coincides with the incubation (this information has not yet been clarified; practically, we focused on one-day difference, characteristic of the flu);

• •    most of the diseased may have an asymptomatic or mild form of the disease, but they are also sources of infection through face-to-face contacts;

• •    the disease may be extremely severe, cause complications that lead to a critical condition,

require long-term treatment in intensive care units, and even lead to a fatal outcome;

• •    a person’s basic level of health (if he or she has or does not have serious chronic diseases) plays a significant role in how the disease will proceed and what outcome it will lead to. Due to the fact that the proportion of people suffering from chronic diseases is much higher among older people, the risk of complications for them is also much higher.

Taking into account these features of COVID-19, we selected a modification of the SEIRD epidemic propagation model as a basis; created ABM provides transitions between corresponding stages for agents-people.

When creating realistic ABM, the results of which could be used as an assessment of development of processes occurring in real life, it is necessary to provide at least two conditions: first, to reproduce the structure of the simulated system as accurately as possible at the selected initial time; second, to achieve the most accurate simulation of actions of agents involved in the modelled processes. In addition, it should be possible to change environment characteristics that affect the agents’ behavior. Typically, such characteristics are entered into ABM as parameters that can be changed during computer experiments. This very approach allows simulating various scenarios for the processes’ development and / or the impact of management measures in order to assess their consequences.

It is important to emphasize here that the structure of agent population should reproduce the differentiation of real community by characteristics that significantly affect the agents’ behavior in the processes that the model is configured to simulate. In our case, this is the differentiation of people by their susceptibility to the infection, and the ways and speed of its transmission. As a minimum, we should ensure that basic demographic characteristics, such as age and gender, as well as some measure of health status, are correctly distributed among the agents’ population. In addition, it is necessary to form families, since it is within families where constant intensive contacts between people take place.

Moscow was chosen as the modeling object. In a megalopolis, we can speak about intensive interactions of residents with more confidence, that is, the SEIRD model is expected to be more plausible. In addition, Moscow faced the COVID-19 problem earlier than other regions, and authorities were forced to take measures that affected development of the epidemic situation.

In addition to the modeling object, it was important to determine which data can be considered reliable enough to be used as a source for the model building. If we talk about data related to population, we should understand that it is quite difficult to separate Moscow from the Moscow agglomeration. There is data on the age and gender composition of the permanent population of Moscow, but there is also shuttle labor migration, there is regular migration, including the unofficial one, and there are huge traffic flows through train stations and airports. All these people can take part in the process of spreading the infection. However, at the first stage of creating the COVID-19 epidemic ABM in Moscow, when developing its prototype, it was important to test the mechanisms of simulating the processes of infection spread and the agents’ passing through the disease stages, which made the task easier. So, we limited ourselves to considering the permanent population of Moscow. In addition, for the purity of the experiment, the processes of natural population movement, birth rate and mortality from other causes, were not taken into account during the simulated period.

If we talk about data related to the proper coronavirus infection, it should be noted that daily published data on a number of infected people do not and cannot provide a whole picture, since it depends on a number of tests performed and testing scheme itself. Thus, at first, testing was conducted mainly among those who had suspicious symptoms, and/or among those who had contacts with already identified patients. However, it is now reliably known about the long incubation period, and a large proportion of asymptomatic patients. In this regard, we considered data on a number of cases to be not reliable enough to base the work of the model on them.

The main source of information used to simulate the processes of new patients’ infection and the disease features were the official guidelines5, prepared by domestic experts-epidemiologists, taking into account the experience of the Chinese, American, and European centers for disease control, the results of scientific research and data prepared by WHO specialists.

The prototype of the COVID-19 epidemic ABM in Moscow was developed at the Central Economic Mathematical Institute of the Russian Academy of Sciences in the Java programming language. The model reads initial data required for building the model, creating a population of agents, and distributing its properties from an external file in Excel format and stores the simulation results in a file of the same format for further processing and analysis.

As well as the creators of the COVID-19 Scenarios model, we considered it important to assess the burden on the health care system, so the presented model calculates the number of necessary beds in hospitals, including intensive care units, at each step of the simulation (which corresponds to one day), in addition to the number of groups of agents at different stages of the disease.

ABM implementation of COVID-19 epidemic

Source data: population of Moscow and its distribution by age and gender; population of agents; the distribution of child births by the age of a mother; the distribution of the population by health level.

Model parameters: initial number of infected; initial reproductive number R₀ (a number of people infected by one virus carrier on average); proportion of mild cases; minimum and maximum duration of the incubation period; minimum and maximum duration of the disease.

Setting the model starting state

Values of the agents’ demographic characteristics such as age and gender are distributed using scaling procedures on the population of agents of a given number in such a way as to reproduce the age and gender structure of the population of Moscow corresponding to the original data in an artificial society. The model also takes into account the differentiation of people by health level, which is set on a scale of “excellent”, “practically healthy”, “weak” (the latter category implies the presence of chronic diseases). Initially, the agents are assigned a basic level of health in accordance with the initial data on the groups ratio, after which a value is adjusted for their age (with ageing, the probability of the agent’s health moving to the worse category increases). Then the agents form families, which uses initial information about the distribution of child births by the age of a mother. An agent “remembers” family ties with the help of individual collections (lists) of immediate family members: spouse; parents; children; siblings (see [19] for more information about the procedures used to simulate family formation in the model).

Simulation of COVID-19 infection propagation processes

At each step of the model, agents are infected from other agents, diseased or infected (except for those who are in hospital, quarantined or self-isolated). Each source agent can transmit the infection further at each step of the simulation in two different ways: to relatives (the probability of getting sick for each relative is assumed to be 0.2) and to outside agents, who are randomly selected from population of agents. The probability of infection for the source agent in the latter case is defined as a ratio of a number of possible infections to the length of the period during which it is considered infectious (the sum of the incubation period and the disease period duration). In case of “successful” infection, a number of possible infections for the source agent is reduced by one, and this agent does not infect anyone else during the simulation step. For newly infected agent by the plan of the disease is determined: the duration of the incubation period, severity of illness and length of hospitalization (including intensive care) and the outcome of the disease – agent’s recovery with the immunity development or death. In both cases, such diseased agent does not participate in the process of spreading the infection in the next steps of the simulation. The specific values of all these parameters are determined for each agent in a probabilistic way in accordance with the rules presented in Table 1.

Table 1. Agents’ characteristics associated with COVID-19 and the ways to determine them

Indicator	Possible values in the model	Way for value determining	Expert evaluations and their source
Stage of the disease	Integer in the range [0, 4]: 0 – susceptible; 1    – infected; 2    – deseased; 3    – recovered; 4    – death	Initial value = 0. Changing in the next simulation steps when moving to the following categories according to the disease course plan
Duration of the incubation period, days	Integer in the interval [Min, Max]	Selected probabilistically using a beta distribution with specified boundaries. The distribution parameters are selected so that the average value ( ≈ 6) matches the expert value (5-7)*	For agents over 18: Min = 2; Max = 14; The average value is 5-7 days. For children: Min = 2; Max = 10*
Severity of the disease	Integer in the range [0, 2]: 0 – mild condition; 1– serious condition; 2 – critical condition.	Default value = 0. With a probability depending on the level of the agent’s health, 1 is assigned to serious cases, and from those who got 1, having a critical condition of the disease are selected with a given probability	80% of patients have the disease in a mild form. The proportion of critically ill patients is 0.25 of all serious patients*
Duration of the desease, days	Integer in the interval [Min, Max]	Selected probabilistically using a beta distribution with specified boundaries. The distribution parameters are selected so that the duration of treatment increases with increasing severity of the disease	For agents over 18: Min = 2; Max = 14; The average value is 5-7 days. For children: Min = 2; Max = 10*

Continuation of Table 1

Indicator Possible values in the model Way for value determining Expert evaluations and their source Hospitalization Integer with values: 0 – necessary; 1 – not necessary Default value = 0. If the severity of the disease is greater than 1, then 1 is set. The agent is placed in the hospital at the current simulation step Intensive care Integer with values: 0 – necessary; 1 – not necessary Default value = 0. If the severity of the disease is greater than 1, then 1 is set and the agent is placed in intensive care at the current simulation step If the severity of the disease is 1, then 1 is set with a probability of 0.33 and the time of the patient’s transfer to the intensive care unit is determined. The probability of transfer to the intensive care unit is calculated taking into account that the need for resuscitation is estimated as 0.5 of the number of the hospitalized**. The time of the crisis and the corresponding transfer of the agent to the intensive care unit is set taking into account the experts’ data – the 8th day since the beginning of the disease* Outcome of the disease Disease stage = 3 Disease stage = 4 Default value = 3. If the agent is in intensive care, then 4 is set with a probability of 0.09 The probability of death is calculated taking into account the official data on the actual lethality for the city of Moscow Number of possible infections Integer indicating the maximum possible number of non-related agents that can be infected by the agent Calculated probabilistically according to the parameter value in decimal format WHO’s estimate dated 20.03.2020***: 2-3, 1 Isolation mode Integer in the range [0, 2]: 0 – free movement; 1    – self-isolation; 2    – isolation If the agent is hospitalized, 2 is set. If the agent falls into a category that has a self-isolation mode, then 1 is set Compiled using the following data: *    Temporary Guidelines of the Ministry of Health of the Russian Federation. Ver. 5. April 8, 2020. Available at: https://xn--80aesfpebagmfblc0a. xn--p1ai/ai/doc/114/attach/ (accessed: May 30, 2020). * * Amendments to the Order of the Ministry of Health of the Russian Federation no. 198n, dated March 19, 2020, “On the temporary procedure for organizing the work of medical organizations in order to implement measures to prevent and reduce the risks of spreading a new COVID-19 coronavirus infection”, dated April 2, 2020. P. 8. * ** How dangerous is coronavirus: Infectivity, lethality and risk groups. RIA. March 20, 2020. Available at: https://ria. ru/20200319/ (accessed: May 30, 2020).

At the end of each step, the statistics on the agent populations’ state are collected; the results are displayed in the model interface window and saved in the output file.

COVID-19 epidemic ABM prototype testing analysis

Figure 1 shows an area of the model interface where the user can set the experiment parameters, and summary results achieved with the specified parameter values at the current modeling step.

In this case – as of September 1, 2020, with the absence of restrictive measures for entire population but compliance with quarantine regulations by hospitalized agents’ family members.

Testing of the model and evaluation of its properties, such as realism, stability of the results obtained, their dependence on various parameters, etc., were carried out using computer experiments. Each experiment scenario included a series of samples, then the results were averaged and its stability (spread of values) was evaluated. A number of agents in all experiments is 100 thousand. During the simulated period, the processes of natural

Figure 1. Interface of the COVID-19 epidemic ABM in Moscow

population movement, such as birth rate and mortality from other causes were not taken into account.

The first series of the experiments was conducted to assess the adequacy of the model’s response to changes in the initial reproductive number. For comparison, the following values were selected: R₀ = 0.9 (if a value is less than one, the epidemic should fade); R₀ = 1.5 (which corresponds to the swine flu indicator) and R₀ = 2.0 – according to WHO’s experts for COVID-19. The dynamics of the infected agents number, obtained from the simulation results at different values of R₀ and in the absence of quarantine measures, is presented in Figure 2 .

The graph in figure 2 shows that the results of modeling using the agent-based approach are similar to the results obtained on the classic SEIRD model. Thus, at R0 = 0.9, a number of infected people is extremely small (the maximum number of infected agents does not exceed 17) and does not increase until the end of the simulated period; at R0 = 2, there is a high peak of infection (11.5–11.6 thousand agents), which falls on May 8–10, and, with R0 = 1.5, the peak is significantly lower (7.1–7.2 thousand agents) and shifted to the right (July 25–27), so that the epidemic does not end by the end of the period, although the process of new agents’ infection is on the wane.

The next series of experiments was aimed at assessing the impact of restrictive measures on the epidemic’s speed and scale. The following options have been calculated for R0 = 2:

• •    option 1– no restrictive measures;

Figure 2. Dynamics of the infected agents number at different values of the initial reproductive number R0 and the absence of quarantine measures

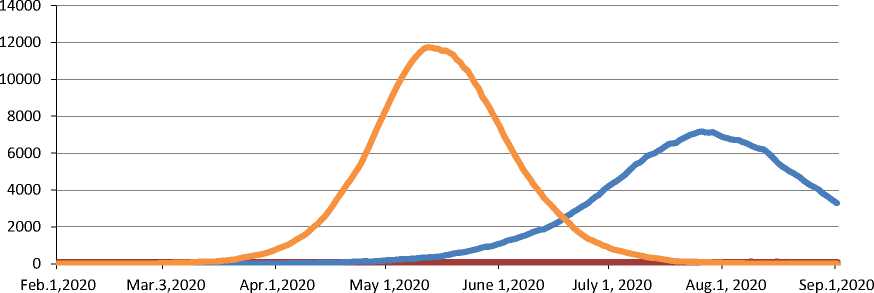
f       R₀ = 0.9     ^^^^e R₀ = 1.5             R₀ = 2.0

Source: calculated according to the results of computer experiments with the COVID-19 epidemic ABM in Moscow.

• •    option 2 – the implementation of the decree of the Moscow mayor, dated March 23, 2020⁶, was simulated in terms of compliance by citizens over the age of 65 with the self-isolation regime starting from March 26 and until September 1. It was considered that citizens of this category are sufficiently disciplined (the probability of their compliance with the order is 0.9);

• •    option 3 – in addition to conditions of option 2, self-isolation of all other categories of citizens, discipline – 0.5.

The simulation results showed that the introduction of restrictive measures can significantly reduce a number of deaths (-16.4%), as well as peak loads on the health system (-26.8%). The simulation results are presented in more detail in Table 2 , where a number

Table 2. Assessment of epidemiological indicators with the absence of quarantine measures and self-isolation of citizens over 65 years of age (R0 = 2)

Indicator	Option 1	Option 2	Option 3
Total number of infected for the entire period, thousand people	12067.922	10083.283 (-16.4%)	Similar to Option 2
Percentage of the infected in the total population, %	95.7	79.9	Similar to Option 2
Maximum number of the required places in hospitals, thousand.	861.120	630.513 (-26.8%)	Similar to Option 2
including intensive care units, thousand.	359.410	257.857 (-28.3%)	Similar to Option 2
requirement peak	May 27	May 26	June 29
Number of deaths, thousand people	105.842	88.433 (-16.4%)	79.098 (-25.3%)
Compiled according to the results of computer experiments with the COVID-19 epidemic ABM in Moscow.

6 On amending the decree of the Moscow Mayor no. 12-UM, dated March 5, 2020: Decree of the Moscow Mayor no. 12-УМ, dated March 23, 2020.

Figure 3. Dynamics of a ratio of agent population groups. Options: a) no restrictive measures; b) self-isolation of citizens over 65 years of age; c) self-isolation of all citizens since April 4, 2020 to May 11, 2020

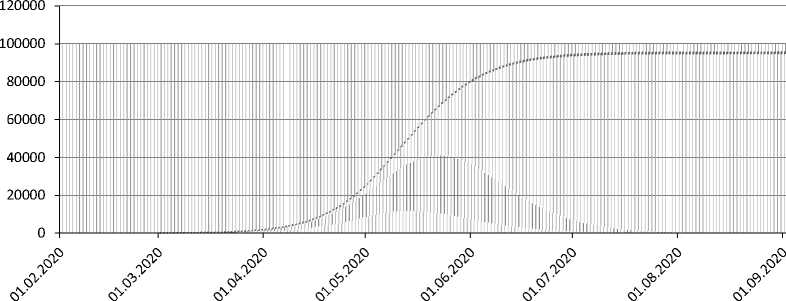
Infected

Diseased

Recovered

Dead

Susceptible

a)

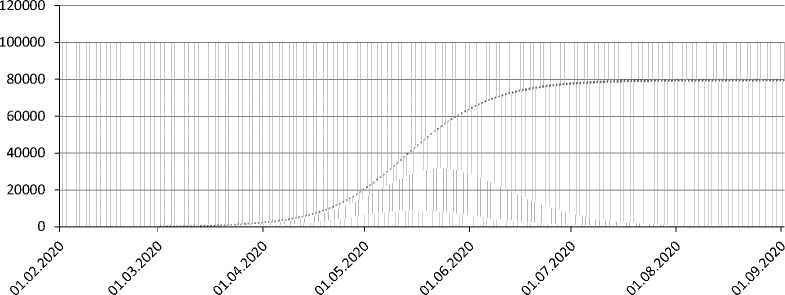
Infected

Diseased

Recovered

Dead

Susceptible

b)

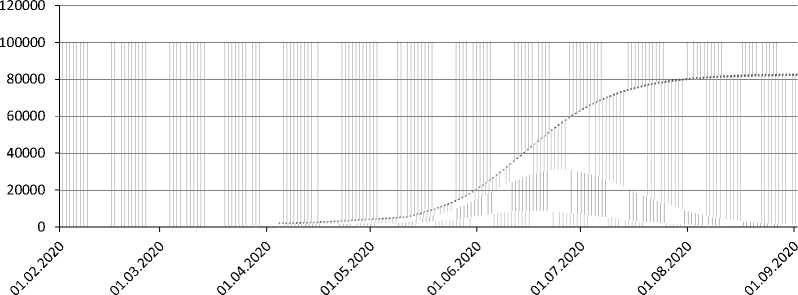
Infected

Diseased

Recovered

Dead

Susceptible

c)

Source: calculated according to the results of computer experiments with the COVID-19 epidemic ABM in Moscow.

of agents and a number of beds required are converted to a scale corresponding to population. In option 3, there is a noticeable improvement only in a number of deaths (-25.3% compared to option 1), and the peak of the disease is pushed back by a month – until June 29–30. The course of the epidemic for studied options is illustrated in Figures 3a-c .

Comparison of different forecast options indicates an adequate response of the model to the introduction of appropriate restrictive measures. As for absolute values of a number of different agent groups, it is obvious that the model needs to be calibrated to clarify the parameters set by experts, primarily the date of the epidemic start and initial number of infected people. In our opinion, the model, calibrated in this way, may be used in solving practical problems related to testing restrictive measures.

It should be noted that observed variation in the results of various samples is quite large, which is caused by the very usage of probabilistic mechanisms for a large number of model parameters on a relatively small agent population. In order to improve the stability of the model, it is necessary to increase the agent population. This will require switching to supercomputer technology. A supercomputer version of the epidemic ABM is planned to be developed on the basis of the MOEBIUS software system created at the Central Economic Mathematical Institute of RAS [20], which allows designing ABM with up to 1 billion agents.

Conclusion

After analyzing the results of testing the presented prototype of the demographic epidemic COVID-19 ABM in Moscow, the following conclusions could be drawn.

The usage of an agent-based approach made it possible to create a realistic epidemiological model that explicitly takes into account: a) the specifics of the course of a particular infectious disease that caused the epidemic; b) the heterogeneity of the region’s population in terms of its susceptibility to infection; c) the individuals’ social ties that significantly affect the frequency of contacts and, as a result, the probability of the infection transmission. A special feature of the presented design, which distinguishes it from other known epidemic ABMs, is the usage of the family formation mechanism, which makes the simulation of contacts as close to reality as possible at the level of an individual agent.

The model showed an adequate response in the course of computer experiments to the variation of the main epidemiological parameters and to the control actions aimed at restricting the infection spread.

Used socio-demographic structure of population and epidemiological characteristics of a particular infection are the parameters of the model, which makes it quite universal and allows adjusting it to the characteristics of other infections and other regions.

The proposed approach to epidemics modeling can be expanded. For example, in ABM, agents may be differentiated simultaneously in terms of their participation in different types of economic activities. Moreover, taking into account intersectoral links, it is possible to build chains of the final product creation, which will allow computer experiments to assess the direct and long-term consequences of the epidemic, various restrictive measures, and measures to support population and business not only for the economy as a whole but also for its individual industries.

Thus, based on the presented epidemic ABM, it is possible to develop universal software packages designed for decision support systems for departmental and regional situation centers.