Cравнение моделей пен, составленных из регулярных и нерегулярных массивов открытых ячеек Гибсона-Эшби
Автор: Корниевский А.С., Наседкин А.В.
Статья в выпуске: 3, 2021 года.
Бесплатный доступ
Работа посвящена исследованию эффективных упругих свойств пенообразных или ячеистых материалов, моделируемых массивами открытых ячеек Гибсона-Эшби регулярной и нерегулярной структуры. В настоящее время существует множество работ, в которых представлены результаты исследований ячеистых материалов теоретическими, численными и экспериментальными методами. Однако в этих работах рассматривались либо регулярные решетки, либо отдельная ячейка, либо модели представительных объемов, не основанные на моделях Гибсона-Эшби. В данной статье помимо регулярной решетки численно исследовались и нерегулярные структуры. Описана математическая постановка задачи гомогенизации, основанная на эквивалентности по энергии пенообразного материала и однородной среды сравнения. Приведены постановки шести краевых задач, решения которых в совокупности позволяют определить полный набор эффективных модулей жесткости для пен с произвольными типами физической и геометрической анизотропий. Все этапы численного исследования были реализованы в конечно-элементном пакете ANSYS. Подробно описаны два алгоритма формирования твердотельных и конечно-элементных моделей нерегулярных решеток Гибсона-Эшби с малой и с большой пористостью. В качестве примера для поликарбонатных пен осуществлены численные расчеты в широком диапазоне пористости. Проведено сравнение значений эффективных упругих модулей для регулярных и нерегулярных решеток и для аналитической модели Гибсона-Эшби. Результаты вычислительных экспериментов показали, что модель Гибсона-Эшби достаточно хорошо описывает поведение высокопористых материалов (с пористостью более 75 %), но при меньших значениях пористости дает менее удовлетворительное предсказание. Отмечено, что при большом числе ячеек статистически регулярные и нерегулярные решетки дают близкие результаты для эффективных модулей. Однако для отдельных структур нерегулярных решеток, особенно при сильно различающихся ячейках в отдельных направлениях, эффективные модули могут иметь существенно отличающиеся значения, а эффективная гомогенная среда может иметь ярко выраженные анизотропные свойства. Эти эффекты обусловлены геометрической анизотропией и концентрацией напряжений в длинных соединительных балках и на стыках балок различных размеров в сильно нерегулярных решетках Гибсона-Эшби. Приведены примеры подобных решеток, и дан анализ разброса значений относительных модулей, характеризующий анизотропию таких структур.
Упругость, высокопористый материал, пена, открытая пористость, гомогенизация, эффективный модуль, модель гибсона-эшби, геометрическая анизотропия, метод конечных элементов, ansys
Короткий адрес: https://sciup.org/146282370
IDR: 146282370 | УДК: 539.3 | DOI: 10.15593/perm.mech/2021.3.07
Текст научной статьи Cравнение моделей пен, составленных из регулярных и нерегулярных массивов открытых ячеек Гибсона-Эшби
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2021PNRPU MECHANICS BULLETIN
На протяжении долгого времени люди использовали относительно сплошные материалы. Так, например, в строительстве активно применяются бетон, сталь, стекло и другие материалы. Между тем в природе для тех же целей используются также пенообразные, клеточные, ячеистые и сотовые структуры (кости, дерево, кораллы и т.п.) Их преимущество состоит в относительно высокой жесткости при малой плотности, в пористости и низкой теплопроводности [1, 2]. В настоящее время клеточные материалы могут эффективно производиться искусственно из различных видов пластика или металлов [3–14]. В связи с этим развитие методов предсказательного моделирования для определения относительной плотности, эффективных физических свойств и оптимальной геометрической структуры пенных материалов является важной задачей. Современные обзоры работ по данным направлениям можно найти в [15–17].
Для моделирования пенообразных и ячеистых структур предложено множество решений, но самым популярным, по-видимому, является ячейка Гибсона– Эшби [18], которая вместе со своими различными модификациями была подробно описана в работах авторов [2, 18–21]. В последнее время было проведено большое количество экспериментов, которые показали, что модели Гибсона–Эшби дают удовлетворительные предсказания физических свойств высокопористых пен с регулярной структурой [9, 11, 12, 22–24].
Нерегулярные пенообразные и ячеистые структуры с клетками, отличными от ячеек Гибсона–Эшби, исследовались теоретическими, экспериментальными и численными методами в [25–32]. Нерегулярные решетки из ячеек Гибсона-Эшби изучались в [33, 34]. Однако в этих работах нерегулярность понималась как различие в размерах базовой ячейки Гибсона–Эшби по осям координат, которая далее при построении представительного объема транслировалась вдоль осей уже без изменений. При расчетах нерегулярных структур в указанных работах отмечалась анизотропия эффективных свойств, вызванная нарушением свойств симметрии геометрий решеток.
В работе исследуются высокопористые упругие материалы, моделируемые массивами ячеек Гибсона–Эшби как регулярной, так и нерегулярной структуры. Вначале дается математическая постановка задачи гомогенизации по методу эффективных модулей для общего случая анизотропного двухфазного материала. Обсуждаются задачи гомогенизации для материалов определенных классов физической и геометрической анизотропии, а также отмечается возможность предельного перехода от задачи гомогенизации двухфазного композита к соответствующей задаче для пористого материала.
В следующем разделе подробно описываются алгоритмы создания твердотельных моделей регулярных и нерегулярных массивов ячеек Гибсона–Эшби средствами геометрического моделирования конечно-элементного пакета ANSYS. Два варианта алгоритмов позволяют создавать нерегулярные структуры с открытой пористостью как для высокопористых, так и для низкопористых пенообразных материалов. Построенные твердотельные структуры позволяют далее легко генерировать качественные гексаэдральные конечно-элементные сетки с управляемыми размерами элементов.
В качестве численного примера рассмотрены регулярные и нерегулярные структуры пористого поликарбоната, рассматриваемого как изотропный материал. Проведено сравнение результатов компьютерных расчетов в ANSYS для модели Гибсона–Эшби, для регулярных и нерегулярных массивов ячеек Гибсона–Эшби в зависимости от пористости. Анализировались эффективные модули Юнга, модули жесткости и коэффициенты Пуассона, а также влияние нерегулярности геометрических структур на анизотропию свойств результирующих гомогенных материалов.
1. Теоретические аспекты метода эффективных модулей
Пусть Q - представительный объем, состоящий из двух частей Q1 и QР . Объем Q1 представляет собой связанную конструкцию Q5 = ^ Qck , состоящую из соединенных между собой трехмерных ячеек Гибсона– Эшби QС. Вторая область QР заполнена гипотетическим упругим материалом с очень малыми упругими жесткостями и моделирует пустоты в пористом материале.
Примем, что материал в области Q5 является упругим, в общем случае анизотропным, и характеризуется плотностью р5 и упругими жесткостями с^р. В области QР для фиктивного материала примем рР = пр5, сОРв = ПСв, П << 1. Таким образом, область Q рассматривается как упругий композит с кусочнонеоднородными плотностью р и упругими модулями c «₽ : р = р e , cав= ce в , X GQ e , e = 5 ’ Р . При этом в случае пористого композита параметр контраста п между модулями различных фаз имеет экстремально малое значение.
Задача гомогенизации состоит в том, чтобы, зная материальные модули и геометрические характеристики фаз композита, определить эффективные свойства с f эквивалентной гомогенной среды. В качестве критерия эквивалентности будем принимать равенство энергии композита U и энергии гомогенной среды U в объеме Q при некоторых одинаковых внешних воздействиях.
Рассмотрим в представительном объеме Q статическую задачу теории упругости для вектора перемещений u = u ( x ) со специальными граничными условиями на внешней границе Г = dQ . Уравнения линейной теории упругости запишем в векторно-матричном виде:
Здесь и далее латинские индексы изменяются в пределах от 1 до 3, а греческие – в пределах от 1 до 6. При переходе от тензорных обозначений Qij, ек,, cijkl к век- торно-матричным обозначениям Фойхта Ta, S^, ca^ используются стандартные формулы соответствия между индексами (ij) ^ а, (kl) ^ Р : (11) ^ 1, (22) ^ 2, (33) ^ 3 , (23) (32) ^ 4, (13) ~ (31) « 5 , (12) - (21) « 6 .
Как часто принимается в теории композитов [35, 36], на внешней границе Г зададим линейные по пространственным координатам x краевые условия для перемещений:
u = L * ( x ) • S o, x еГ , (5)
Где S o = { S 01 , S 02 , S 03 , S 04 , S 05 , S 06 } = { £ 011 , £ 022 , £ 033 ,2 e 023 ,
2e013,2s012}; S op - некоторые не зависящие от x постоянные величины.
Положим в (5) лишь одну из компонент массива So отличной от нуля:
S . 5 . S 0 , (6)
где 5^ - символ Кронекера, индекс Z принимает какое-то целое число от 1 до 6; So - некоторая постоянная величина.
В соответствии с общей теорией, после решения задачи (1)-(6) и нахождения полей напряжений с^., можно определить столбец матрицы эффективных модулей eff c с номером Z :
cf =<C j > /е 0 , (7)
где е0 = S 0 при Z = 1, 2, 3 , е0 = 2 S 0 при Z = 4, 5, 6, а через < • > обозначено осреднение по представительному объему,
<•>= — Г ( • ) d Q . (8)
| Q | Jn
В общем случае анизотропии требуется решить шесть задач (1)-(6) при Z = 1, 2, ..., 6, которые в совокупности позволяют найти эффективные модули для всех шести столбцов матрицы c eff . Как несложно заметить, первые три задачи с Z = 1, 2, 3 являются задачами о растяжении объема Q вдоль осей xx , x 2, х3 соответственно, а задачи с Z = 4, 5, 6 являются задачами о сдвигах представительного объема в различных плоскостях.
Описанный выше метод эффективных модулей основывается на том, что для задач (1)–(6) для композитного тела с модулями c и для гомогенного тела с мо-_ eff ~ дулями c при одинаковых внешних воздействиях (5), (6) оказываются одинаковыми средние деформации < S >=< S0 >= So и выполняется тождество Хилла [35, 36] < S • T >=< S > • < T >. Поэтому принятие условия равенства потенциальных энергий U = Uo, U =< S • T > /2 , U0 =< S0 • T0 > /2 влечет за собой равен- ство средних напряжений < T >=< To >= То, что и обосновывает формулы (7), (8).
В случае материала ромбической системы матрица упругих жесткостей имеет девять независимых коэффициентов. Например, матрицу податливостей s = с - 1 можно представить в виде
Для изотропного материала имеется только два независимых модуля, поскольку Ex = E2 = E3 = E, v12 = v13 =v23 =v , G = G = G23 = G , G = E/(1 +v)/2 .
Отметим, что если исходные модули двух фаз композита обладали каким -то одним и тем же типом анизотропии, то его эффективные модули могут иметь более сложный тип анизотропии, поскольку представительный объем может не иметь тех свойств симметрии, которые имеются у материальных свойств фаз. Поэтому, решая задачи (1)-(6) при различных Z и определяя по (7), (8) эффективные модули, надо проверять, каким типом анизотропии будет обладать гомогенный материал. При решении задач (1)-(6) численно методом конечных элементов равенства некоторых эффективных модулей могут выполняться не точно, а с некоторой погрешностью. Естественно, для оценки типа анизотропии эффективных модулей этой вычислительной погрешностью можно пренебречь.
В приводимом ниже численном примере рассматривался поликарбонат [43], который является изотропным материалом. Поэтому для регулярного представительного объема с пустотами эквивалентный гомогенный материал получается изотропным, и для нахождения его эффективных констант можно решить всего одну задачу (1)-(6), например, с Z = 1. Если же представительный объем не имеет геометрической изотропии, то надо решать все шесть задач (1)–(6) и оценивать степень различия модулей из решений разных задач и получаемых модулей. При этом, как следует из доказательства для более общего случая электроупруго-го композита [44], матрица эффективных модулей должна быть симметричной, т.е. должны выполняться eff eff равенства Сав = Сва .
Описанная выше методология применима к двухфазным упругим композитам с условиями полного контакта на границе раздела фаз Г i = dQ 5 ndQ p ,
[ u ] = 0; [ L * ( n ) ■ T ] = 0; x еГ , (10) где [( • )] = ( • ) s - ( • ) p - скачок функции (•) через интерфейсную границу Γ i ; n – вектор единичной нормали к Γ i , внешней, например, по отношению к области Ω s .
Условие (10) выражает непрерывность перемещений и вектора напряжений на межфазной границе Γ i . Для рассматриваемого случая, когда область Ω p заполнена материалом с очень малыми модулями жесткости, можно решать задачу (1)–(6) только для области Ω s с границей Γ s = ∂Ω s = Γ e ∪ Γ i , Γ e = Γ∩∂Ω s , задавая условие (6) только на границе Γ e и считая границу Γ i свободной от напряжений.
L * ( n ) ■ T = 0, x еГ . (11)
При малых модулях жесткости c p = П с а в , П << 1, эффективные модули, рассчитанные по (7) из решения задачи (1)–(4) в Ω , (5), (6) на Γ , (10) и из решения задачи (1)–(4) в Ω s , (5), (6) на Γ e и (11), будут практически совпадать. При этом осреднение по (8) в (7) для второй задачи надо заменить на осреднение по объему Q функций (•), заданных только на Q s :
<•>=<•> s = —f ( • ) d Q . (12) | Q | J q s
Для высокопористых материалов первый вариант задачи гомогенизации более удобен для теоретического обоснования метода, а второй вариант более удобен для практического решения. В связи с этим далее будем использовать второй вариант с решением задачи гомогенизации только в Ω s .
2. Описание алгоритма построения представительного объема
Согласно подходу Гибсона–Эшби [2, 18–21], на простейшем уровне трехмерный высокопористый материал или пену можно смоделировать как массив кубических элементов, состоящий из тонких балок. Примем, что отдельные ячейки имеют вдоль всех осей декартовой системы координат длину L , все балки имеют одинаковое квадратное поперечное сечение со стороной h , а размер внутреннего куба, измеренный как расстояние между серединами его противоположных балок, равен a . На рис. 1, а изображен один из вариантов твердотельной модели ячейки Гибсона–Эшби, сгенерированной в пакете ANSYS, а на рис. 1, б показана та же модель в плоскости XY ( x = X , x = Y , x = Z ).
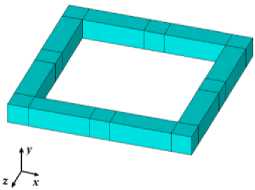
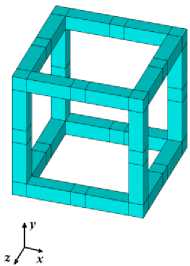
При построении ячейки Гибсона–Эшби вначале строится основная часть ячейки, состоящая из внутреннего кубического остова, а затем все ее соединения. На рис. 2, а приведен пример построения нижних балок основной части ячейки. Отметим, что структура состоит из 16 объемов двух видов. Это необходимо для того, чтобы в дальнейшем не было проблем с генерацией регулярных конечно-элементных сеток при разбиении твердотельной модели на гексаэдральные конечные элементы. Именно для этого были размещены дополнительные кубические объемы на местах контактов с соединительными балками. Затем аналогичным образом достраивается вся основная (внутренняя) часть ячейки (рис. 2, б). На последнем этапе построения геометрии отдельной ячейки строятся ее соединительные балки, и в итоге получается ячейка Гибсона–Эшби (см. рис. 1).
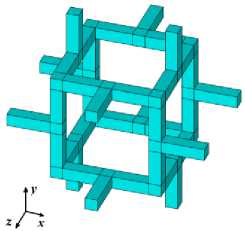
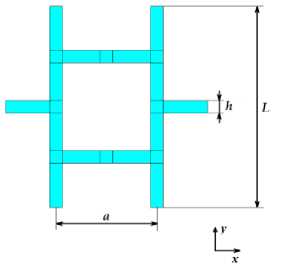
Рис. 1. Вариант ячейки Гибсона–Эшби: а – общий вид в трехмерном пространстве; б – вид в плоскости XY
Fig. 1. Variant of the Gibson–Ashby cell: a a general view in three-dimensional space; b a view in XY plane
а
Рис. 2. Построение кубического каркаса ячейки: а – нижняя часть; б – полный кубический каркас
б
Fig. 2. Construction of the cubic skeleton for a cell: a – a bottom part; b – a full cubic skeleton
Отметим, что при варьировании размера стороны поперечного сечения балки h изменяется и пористость всей структуры. Если постепенно увеличивать толщину балки, то можно прийти к случаю, когда геометрические объемы, из которых состоит ячейка, начнут пересекаться друг с другом. Поэтому для случаев больших толщин h была предложена другая модель. Предположим, что h > a /2. В таком случае кубики, которые расположены в углах и в серединах балок основной части ячейки, будут настолько большими, что будут пересекаться друг с другом. Чтобы избежать таких перекрытий, дополнительно выделяются линии предполагаемых пересечений больших кубов и затем по всем граничным линиям строятся непересекающиеся объемы в форме параллелепипедов. Затем аналогичным образом достраивается основная часть ячейки, и добавляются соединительные балки. На рис. 3, а приведен пример построения нижних балок основной части ячейки для случая h > a /2, а один из вариантов сгенерированной итоговой ячейки показан на рис. 3, б .
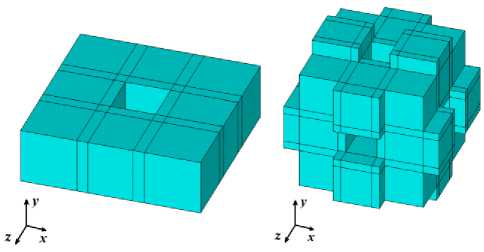
Рис. 3. Построение ячейки при больших толщинах балок: а – нижняя часть кубического каркаса; б – полная ячейка
-
Fig. 3. Construction of a cell for large thicknesses of beams: a – a lower part of the cubic skeleton; b – a full cell
Как известно [3, 9, 22], при производстве искусственных пен размеры отдельных пор могут достаточно сильно варьироваться. Поэтому далее будут рассмотрены алгоритмы для построения решеток двух видов: регулярной и нерегулярной. Регулярная решетка – это структура, которая состоит из ячеек Гибсона–Эшби одинаковой внутренней структуры. Нерегулярная решетка строится из ячеек, у которых размеры внутренних кубических каркасов выбираются случайным образом.
В случае регулярной решетки ее сборка из отдельных ячеек Гибсона–Эшби не вызывает никаких трудностей. Так как все ячейки идентичны, то они идеально стыкуются между собой соединительными балками. В случае нерегулярной решетки алгоритм становится более сложным. Примем, что толщина балок h одинакова для всех ячеек, это обеспечивает наиболее простой контакт соединительных балок различных ячеек. Заметим, что при больших значениях h размеры основной внутренней части ячейки могут меняться в меньших пределах, чем при малых h . Поэтому при толстых балках решетка становится более регулярной. В связи с этим для нерегулярной решетки мы будем рассматривать только случай, когда h < a /2.
Обратим внимание, что в представленной модели все ячейки имеют одинаковый размер L . Но для каждой ячейки размер внутренней части a выбирается случайным образом. При уменьшении размера a внутренний кубик ячейки также уменьшается, но увеличиваются длины соединительных балок. Напротив, при возрастании a внутренний кубик ячейки увеличивается, но уменьшаются длины балок. На рис. 4 изображены две ячейки с существенно различными размерами их внутренних частей.
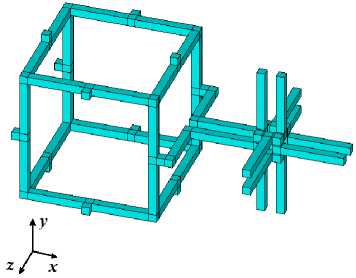
Рис. 4. Цепочка из двух ячеек Гибсона–Эшби с существенно различными размерами кубических каркасов
-
Fig. 4. A chain of two Gibson–Ashby cells with significantly different sizes of cube skeletons
Перед началом геометрического построения всей структуры с использованием генератора случайных чисел создается массив, который содержит значения a для всех ячеек решетки. На этом этапе необходимо задать ограничения на а . Очевидно, что а е (2 h , L - 2 h ). Но если размер a будет близок к крайним значениям, то при построении появятся объемы, у которых размеры в одном измерении будут много меньше размеров в других измерениях. В такой ситуации нужно будет генерировать или очень много конечных элементов с пропорциональными размерами, или использовать элементы с непропорциональными размерами по осям. Оба варианта являются плохими для расчетов. В первом варианте размеры конечно-элементных матриц будут очень большими, и расчеты будут проводиться достаточно долго. Второй вариант может приводить к большим ошибкам в конечно-элементных решениях. В связи с этим ограничения на размер a были изменены следующим образом: а е (2 h + 5, L -2 h -5), 5 = 0,01 L .
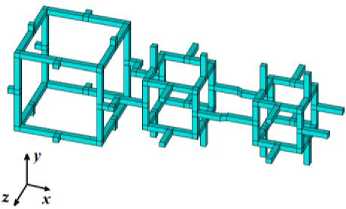
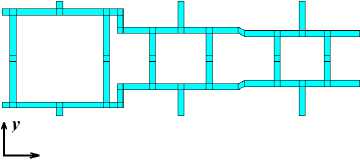
После того как массив со значениями a сгенерирован, в цикле строятся ячейки вдоль координатных осей по аналогии с регулярной решеткой. Так как размеры основных частей каждой ячейки различные, то их необходимо соединить дополнительными балками. Эти дополнительные балки могут быть двух видов. В случае если расстояние между балками двух ячеек небольшое (меньше h ), то дополнительные балки строятся под наклоном, как показано на рис. 5, между крайней правой и центральной ячейками. В случае если расстояние между балками больше толщины балки, то дополнительные элементы строятся перпендикулярно, как показано на рис. 5, между центральной и крайней левой ячейками.
а
X
б
Рис. 5. Нерегулярная цепочка из трех ячеек Гибсона–Эшби: а – общий вид в трехмерном пространстве; б – вид в плоскости XY
-
Fig. 5. An irregular chain of three Gibson–Ashby cells: a – a general view in a three-dimensional space; b – a view in plane XY
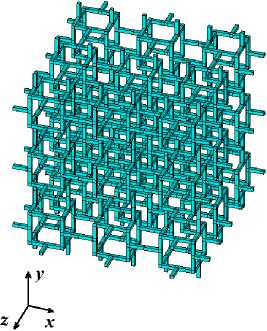
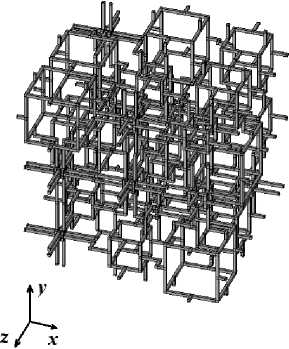
На рис. 6 для наглядности приведены примеры регулярной ( а ) и нерегулярной ( б ) решеток, включающих по три ячейки вдоль каждой оси. Как можно заметить, в нерегулярном случае ячейки с большими каркасами могут генерироваться в случайных местах решетки. Естественно, при этом ячейки с маленькими каркасами концентрируются в других местах. Такое расположение, очевидно, может приводить к геометрической анизотропии каркаса, что повлечет за собой и анизотропию эффективной среды композита. Далее это будет подтверждено численными экспериментами.
Так как задачи гомогенизации решались численно в ANSYS, то твердотельный представительный объем необходимо было разбить на конечные элементы. Для этих целей был выбран стандартный конечный элемент SOLID185 из библиотеки ANSYS, который имеет восемь узлов с тремя степенями свободы перемещений в каждом узле. Средний размер конечных элементов был принят равным L/20. В результате из твердотельной модели в ANSYS была создана конечно-элементная сетка, включающая только гексаэдральные элементы.
Отметим, что в силу линейности задач гомогенизации значения эффективных модулей, вычисленные по
(7), (8) или по (7), (12), будут одинаковыми при геометрических структурах представительных объемов с подобными значениями L , a, h и 5 . Поэтому можно принять, например, L = 1 (м), и a, h и 5 задавать как относительные размеры (отнесенные к L ).
а
б
Рис. 6. Регулярная ( а ) и нерегулярная ( б ) решетки
Fig. 6. Regular ( a ) and irregular ( b ) lattices
3. Численные результаты
Как отмечалось выше, при вычислительных экспериментах рассматривался поликарбонат, который считался линейным изотропным упругим материалом. Для расчетов использовались следующие материальные константы [43]: плотность р5 = 1200 кг/м3; модуль Юн га Es = 2,378 ГПа, коэффициент Пуассона v5 = 0,37.
Представительный объем как для регулярной, так и для нерегулярной решетки был составлен из двадцати семи ячеек Гибсона–Эшби (по три ячейки вдоль каждой оси). Расчеты проводились при различной пористости p , которая варьировалась при задании толщины балок h . Для регулярных решеток были проведены численные эксперименты при пористости p от 5 до 99 %, а для нерегулярных решеток – от 62 до 99 %. Все результаты далее приводятся в относительных величинах: eff s
r ( c ав ) = c ав / c ав — отношение компонент матриц жесткостей; r ( E ) = Et eff / E j - отношение модулей Юнга, r( v ij ) = v eff I v j - отношение коэффициентов Пуассона. Здесь c ав , E eff , v f - значения эффективных модулей пористого тела, а cs , Es , ν s – соответствующие значения этих же модулей для материала матрицы композита (т.е. для тела с нулевой пористостью).
Согласно одной из моделей Гибсона–Эшби для изотропного материала, относительное значение модуля Юнга равно квадрату относительной плотности, умноженному на некоторый коэффициент. Для открытых ячеек Гибсона–Эшби при преобладающих деформациях растяжения-сжатия этот коэффициент можно принять за единицу, и формулу для относительного модуля Юнга можно представить в виде [2, 18–23]
r ( E G ) = E GA I Es = ( p G A I p s ) 2 = (1 - p ) 2 . (13)
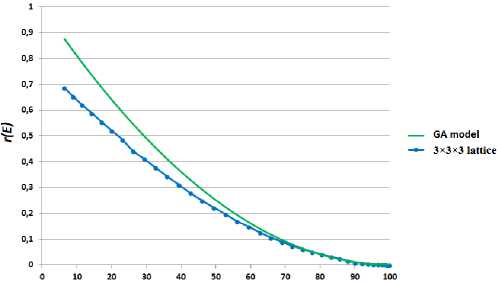
На рис. 7 изображены графики зависимостей от пористости относительных модулей Юнга для одной ячейки Гибсона–Эшби и для регулярной решетки из двадцати семи ячеек Гибсона–Эшби. Зеленая линия соответствует значениям относительных модулей Юнга для модели Гибсона–Эшби, рассчитанным по формуле (13). Синяя линия соответствует значениям, полученным численными экспериментами в ANSYS из решений задач гомогенизации (1)–(4) в Ω s , (5), (6) на Γ e , (11), (7), (12). Из графиков, приведенных на рис. 7, видно, что формула (13) дает значения, близкие к полученным для решетки ячеек Гибсона-Эшби, с размерами 3х 3х 3 только для высокопористых пен.
Пористость, %
Рис. 7. Зависимости относительного модуля Юнга от пористости для модели Гибсона–Эшби и регулярной решетки
Fig. 7. Dependences of the relative Young's modulus on porosity for the Gibson–Ashby model and for a regular lattice
На рис. 8–11 изображены графики зависимостей от пористости относительных модулей Юнга r(E), коэффициента Пуассона r(v) и модулей жесткости r(с j) и r(с2) для регулярных и нерегулярных решеток из ячеек Гибсона–Эшби. При этом на рис. 8 приведена также зеленая кривая, соответствующая значениям относительных модулей Юнга, полученным по формуле (13). Синие кривые на рис. 8–11 построены по значениям, полученным для регулярной решетки, а красные области содержат значения, полученные для нерегулярных решеток. Здесь следует отметить, что для нерегулярных решеток размеры ячеек выбирались случайным образом, и поэтому получаемые результаты изменялись от одного вычислительного эксперимента к другому. Для уменьшения влияния случайности для каждой фиксированной толщины балок проводилось по пять расчетов и осуществлялось дополнительное усреднение коэффициентов матрицы эффективных упругих модулей (9) до модулей изотропного материала.
Для дальнейшей обработки результатов использовались статистические методы с вычислением доверительных интервалов по следующей методологии [45]. Пусть w , w , …, w – значения для одной выборки относительных эффективных модулей с числом степеней свободы f = n -1 при малом числе испытаний n . Тогда среднее арифметическое w и выборочное стандартное отклонение s определялись в виде w=12Lwn s=.112L(w -w)2, (14) n =1 у f 1
а для расчета доверительного интервала Δ w среднего значения w при t -распределении t ( P , f ) с доверительной вероятностью P использовалась формула
А w = tCPifll (15) n с критическим значением t-критерия Стьюдента t(P, f) = 2,78 при P = 0,95, n = 5, найденным из таблицы A.3 [45].
Проводя вычисления по (14), (15) для значений w ( p ), можно построить зависимости от пористости p верхних и нижних значений относительных эффективных модулей w ±Δ w с доверительными интервалами Δ w . Сглаженные кривые красного цвета получены аппроксимацией значений доверительных интервалов. Они определяют на рис. 8–11 границы областей, в которых с доверительной вероятностью 95% находятся значения эффективных модулей w ±Δ w для нерегулярных решеток из ячеек Гибсона–Эшби.
Из приведенных графиков видно, что значения, полученные для нерегулярных решеток, могут иметь достаточно большой разброс. Однако они сохраняют общую тенденцию и за исключением значений относительных коэффициентов Пуассона близки к значениям, полученным для регулярных решеток. Но, как известно [31, 46], эффективные коэффициенты Пуассона пористых материалов наиболее существенно зависят от микроструктуры, и даже тенденции их изменения от порис- тости могут меняться в зависимости от значений коэффициентов Пуассона соответствующих сплошных материалов и внутренней структуры представительных объемов.
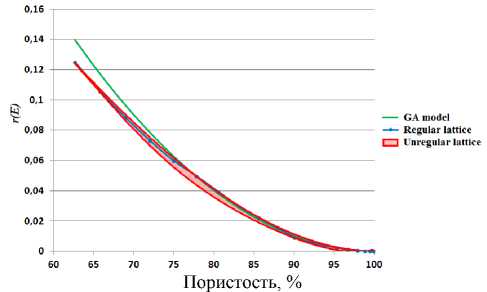
Рис. 8. Зависимости относительного модуля Юнга от пористости для модели Гибсона–Эшби и для регулярных и нерегулярных решеток
Fig. 8. Dependences of the relative Young's modulus on porosity for the Gibson-Ashby model and for regular and irregular lattices
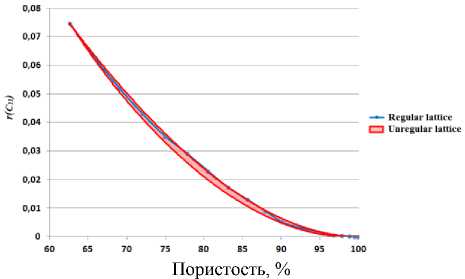
Рис. 9. Зависимости относительного модуля жесткости r ( с, ,) от пористости для регулярных и нерегулярных решеток Fig. 9. Dependences of the relative stiffness modulus r ( с, J on porosity for regular and irregular lattices
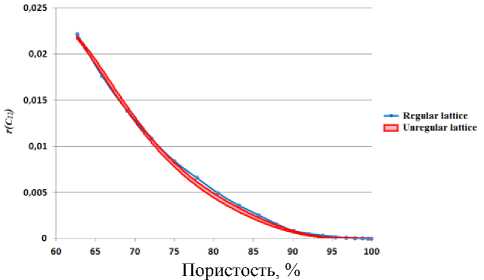
Рис. 10. Зависимости относительного модуля жесткости r ( с 2) от пористости для регулярных и нерегулярных решеток
Fig. 10. Dependences of the relative stiffness modulus r ( с 2) on porosity for regular and irregular lattices
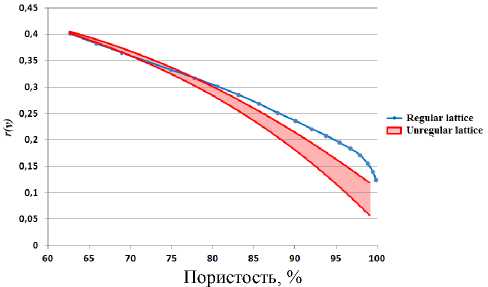
Рис. 11. Зависимости относительного коэффициента Пуассона от пористости для регулярных и нерегулярных решеток
Fig. 11. Dependences of the relative Poisson's ratio on porosity for regular and irregular lattices
Другим интересным результатом является то, что нерегулярная решетка может не сохранять изотропные свойства материала матрицы композита. Для анализа этого явления были рассчитаны относительные отклонения эффективных модулей для композитов с нерегулярными решетками. Так, были вычислены следующие величины: 5 ( E ) = (| E f - E ff | / E eff )100 % - относительные отклонения модулей Юнга; б( c ae , c Yz ) = = (I c f — c y| f I / c ав )100 % - относительные отклонения модулей жесткости c ав и c Yz ; 5 ( v ) = = (I v en -v eff |/v e 1 ff )100 % - относительные отклонения коэффициентов Пуассона.
На рис. 12 приведены графики средних относительных отклонений для модулей жесткости c и c (красная кривая), модулей c и c (зеленая кривая), модулей Юнга (синяя кривая) и коэффициентов Пуассона (желтая кривая). Интересно отметить, что зависимости от пористости относительных отклонений 5 ( q р c 33) и 5 ( E ) очень близки, а поэтому синяя кривая практические совпадает с красной и не видна на рис. 12.
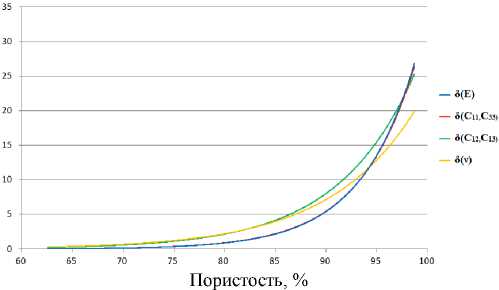
Рис. 12. Разброс относительных модулей нерегулярных решеток, характеризующий их анизотропию
Fig. 12. Scatter of the relative moduli for irregular lattices characterizing their anisotropy
На рис. 12 изображены аппроксимации средних относительных отклонений. Видно, что они не превышают 30 %, однако их неосредненные значения в некоторых случаях могут быть гораздо больше, особенно для высокопористых структур. Приведенные результаты подтверждают мысль, что пористые пены с нерегулярной решеткой могут иметь достаточно выраженные анизотропные свойства, даже если материалы их каркасов являются изотропными. Эта анизотропия обусловлена возможной несимметричностью геометрий и большими напряжениями в нерегулярных решетках.
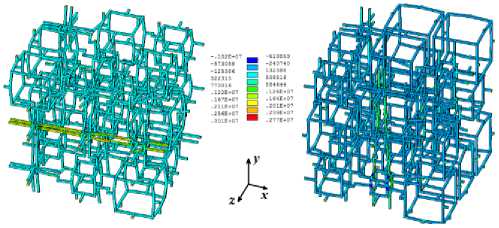
На рис. 13 приведены примеры расчетов двух задач гомогенизации для различных структур с нерегулярными решетками, в которых наблюдаются большие концентрации напряжений в ячейках вдоль одной оси. Обратим внимание, что каркасы этих ячеек имеют небольшие размеры относительно других ячеек. Чем меньше каркасы, тем длиннее их соединительные балки и, соответственно, наблюдаются большие напряжения в этих балках и вблизи данных ячеек [32, 33, 47].
б
а
Рис. 13. Концентрация напряжения на соединительных балках при деформации вдоль оси x ( а ) и оси y ( б )
Fig. 13. Stress concentration on the connecting beams during deformation along the x -axis ( a ) and y -axis ( b )
Так, на рис. 13, а изображено распределение x -компоненты напряжения а.к=а11 после растяжения вдоль оси Ox . Из данного рисунка видно, что непосредственно в части представительного объема, где длинные соединительные балки выстроены вдоль оси Ox , наблюдается наибольшее напряжение. Аналогичная тенденция видна на рис. 13, б , но, в отличие от рис. 13, а , на нем изображено распределение y -компоненты напряжения а =g22 после растяжения вдоль оси Oy другой нерегулярной решетки.
Отметим, что здесь представлены результаты для регулярных и нерегулярных решеток, составленных из трех ячеек Гибсона–Эшби вдоль каждой оси. При большем числе ячеек в регулярных и нерегулярных решетках статистически получаются более близкие ре- зультаты для эффективных упругих модулей, а эффекты концентрации напряжений нивелируются. Однако для отдельных вариантов сильно нерегулярных решеток эффективные модули по-прежнему могут принимать экстремальные значения.
Разработанные модели нерегулярных структур из ячеек Гибсона–Эшби могут использоваться в специализированном программном обеспечении для компьютерного дизайна пенообразных материалов, как в рамках приближений линейной теории упругости, так и для исследования их нелинейного поведения.
Заключение
Было проведено исследование эффективных упругих свойств пористого пенного материала, моделируемого массивами ячеек Гибсона–Эшби с регулярной и нерегулярной структурой. Разработан программный инструментарий на языке APDL ANSYS, позволяющий строить такие массивы ячеек, получать из них конечно-элементные модели с управляемыми характеристиками, решать численно задачи гомогенизации и определять полный набор эффективных модулей жесткости для материалов произвольного типа анизотропии. Вычислительные эксперименты для поликар-бонатных пен показали, что для нерегулярных решеток может наблюдаться достаточно существенный разброс значений упругих модулей, особенно для эффективных коэффициентов Пуассона. Отмечено, что для нерегулярных решеток характерно появление геометрической анизотропии эффективных свойств композита, которая может достаточно сильно проявляться для высокопористых пен.
С использованием разработанных конечно-элементных технологий в дальнейшем предполагается исследовать свойства представительных объемов из ячеек Гибсона–Эшби большой размерности, а также нанострук-турированные пены [48] по теории поверхностных напряжений Гуртина–Мурдоха путем добавления в разработанные модели поверхностных конечных элементов [49–51].
Работа выполнена при финансовой поддержке РФФИ (грант № 20-31-90057).
Acknowledgments
This work was funded by the Russian Foundation for Basic Research based on the Research Project No. 20-31-90057.
Список литературы Cравнение моделей пен, составленных из регулярных и нерегулярных массивов открытых ячеек Гибсона-Эшби
- Cellular ceramics: structure, manufacturing, properties and applications. Scheffler M., Colombo P. (eds.). - John Wiley & Sons, 2005. doi: 10.1002/3527606696
- Gibson L.J., Ashby M.F. Cellular solids: structure and properties. - Cambridge, UK: Cambridge University Press, 1997. - 510 p. doi: 10.1017/CBO9781139878326
- Alabort E., Barba D., Reed R.C. Design of metallic bone by additive manufacturing // Scr. Mater. - 2019. - Vol. 164. - P. 110-114. doi: 10.1016/j.scriptamat.2019.01.022
- Alsalla H., Hao L., Smith C. Fracture toughness and tensile strength of 316L stainless steel cellular lattice structures manufactured using the selective laser melting technique // Mater. Sci. Eng. A. - 2016. - Vol. 669. - P. 1-6. doi: 10.1016/j.msea.2016.05.075
- Study of the compression behaviour of Ti6Al4V trabecular structures produced by additive laser manufacturing / M. Benedetti, J. Klarin, F. Johansson, V. Fontanari, V. Luchin, G. Zappini, A. Molinari // Materials. - 2019. - Vol. 12, iss. 9. - Article 1471. doi: 10.3390/ma12091471
- Bianchi G., Gianella S., Ortona A. Design and additive manufacturing of periodic ceramic architectures // J. Ceram. Sci. Tech. - 2017. - Vol. 08, iss. 01. - P. 59-66. doi: 10.4416/JCST2016-00088
- Manufacturing and characterization of metal-supported solid oxide fuel cells / P. Blennow, J. Hjelm, T. Klemensø, S. Ramousse, A. Kromp, A. Leonide, A. Weber // J. Power Sources. - 2011. - Vol. 196, iss. 17. - P. 7117-7125. doi: 10.1016/j.jpowsour.2010.08.088
- Fleck N.A., Deshpande V.S., Ashby M.F. Micro-architectured materials: past, present and future // Proc. Royal Soc. Lond. A. - 2010. - Vol. 466, iss. 2121. - P. 2495-2516. doi: 10.1098/rspa.2010.0215
- Elastic behavior of multi-scale, open-cell foams / L. Maheo, P. Viot, D. Bernard, A. Chirazi, G. Ceglia, V. Schmitt, O. Mondain-Monval // Compos. Part B: Eng. - 2013. - Vol. 44, iss. 1. - P. 172-183. doi: 10.1016/j.compositesb.2012.06.006
- Open-cellular copper structures fabricated by additive manufacturing using electron beam melting / D.A. Ramirez, L.E. Murr, S.J. Li, Y.X. Tian, E. Martinez, J.L. Martinez, B.I. Machado, S.M. Gaytan, F. Medina, R.B. Wicker // Mater. Sci. Eng. A. - 2011. - Vol. 528, iss. 16-17. - P. 5379-5386. doi: 10.1016/j.msea.2011.03.053
- Design and compressive behavior of controllable irregular porous scaffolds: based on Voronoi-tessellation and for additive manufacturing / G. Wang, L. Shen, J. Zhao, H. Liang, D. Xie, Z. Tian, C. Wang // ACS Biomater. Sci. Eng. - 2018. - Vol. 4, iss. 2. - P. 719-727. doi: 10.1021/acsbiomaterials.7b00916
- Evaluation of topology-optimized lattice structures manufactured via selective laser melting / Z. Xiao, Y. Yang, R. Xiao, Y. Bai, C. Song, D. Wang // Mater. Des. - 2018. - Vol. 143. - P. 27-37. doi: 10.1016/j.matdes.2018.01.023
- Microstructure and mechanical properties of aluminium alloy cellular lattice structures manufactured by direct metal laser sintering / C. Yan, L. Hao, A. Hussein, P. Young, J. Huang, W. Zhu // Mater. Sci. Eng. A. - 2015. - Vol. 628. - P. 238-246. doi: 10.1016/j.msea.2015.01.063
- Plastic deformation, failure and energy absorption of sandwich structures with metallic cellular cores / F. Zhu, G. Lu, D. Ruan, Z. Wang // Int. J. Prot. Struct. - 2010. - Vol. 1, iss. 4. - P. 507-541. doi: 10.1260/2041-4196.1.4.507
- Overview and comparison of modelling methods for foams / A. Hössinger-Kalteis, M. Reiter, M. Jerabek, Z. Major // J. Cell. Plast. - First Published December 15, 2020. - P. 1-51. doi: 10.1177/0021955X20966329
- Pan C., Han V., Lu J. Design and optimization of lattice structures: A review // Appl. Sci. - 2020. - Vol. 10. - Article 6374. doi: 10.3390/app10186374
- Srivastava V., Srivastava R. On the polymeric foams: modeling and properties // J. Mater. Sci. - 2014. - Vol. 49. - P. 2681-2692. doi: 10.1007/s10853-013-7974-5
- Gibson L.J., Ashby M.F. The mechanics of three-dimensional cellular materials // Proc. Royal Soc. Lond. A, 1982. - Vol. 382, iss. 1782. - P. 43-59. doi: 10.1098/rspa.1982.0088
- Ashby M.F. The mechanical properties of cellular solids // Metall. Mater. Trans. A. - 1983. - Vol. 14, iss. 9. - P. 1755-1769. doi: 10.1007/BF02645546
- Ashby M.F. The properties of foams and lattices // Phil. Trans. R. Soc. A. - 2006. - Vol. 364, iss. 1838. - P. 15-30. doi: 10.1098/rsta.2005.1678
- Gibson L.J. Biomechanics of cellular solids // J. Biomech. - 2005. - Vol. 38. - P. 377-399. doi: 10.1016/j.jbiomech.2004.09.027
- Avalle M., Scattina A. Mechanical properties and impact behavior of a microcellular structural foam // Lat. Am. J. Solids Struct. - 2014. - Vol. 11, iss. 2. - P. 200-222. DOI: S1679-78252014000200004
- Uhlířová T., Pabst W. Conductivity and Young's modulus of porous metamaterials based on Gibson-Ashby cells // Scr. Mater. - 2019. - Vol. 159. - P. 1-4. doi: 10.1016/j.scriptamat.2018.09.005
- Multiscale deformation of open cell aluminum foams / J. Zhou, Z. Gao, S. Allameh, E. Akpan, A.M. Cuitino, W.O. Soboyejo // Mech. Adv. Mater. Struct. - 2005. - Vol. 12, iss. 3. - P. 201-216. doi: 10.1080/15376490590928552
- Andresen S., Bäger A., Hamm C. Eigenfrequency maximisation by using irregular lattice structures // J. Sound Vib. - 2020. - Vol. 465. - Article 115027. doi: 10.1016/j.jsv.2019.115027
- Marvi-Mashhadi M., Lopes C.S., LLorca J. Modelling of the mechanical behavior of polyurethane foams by means of micromechanical characterization and computational homogenization // Int. J. Solids Struct. - 2018. - Vol. 146. - P. 154-166. doi: 10.1016/j.ijsolstr.2018.03.026
- Marvi-Mashhadi M., Lopes C.S., LLorca J. Effect of anisotropy on the mechanical properties of polyurethane foams: An experimental and numerical study // Mech. Mater. - 2018. - Vol. 124. - P. 143-154. doi: 10.1016/j.mechmat.2018.06.006
- Mukhopadhyay T., Adhikari S. Equivalent in-plane elastic properties of irregular honeycombs: An analytical approach // Int. J. Solids Struct. - 2016. - Vol. 91. - P. 169-184. doi: 10.1016/j.ijsolstr.2015.12.006
- Mukhopadhyay T., Adhikari S. Effective in-plane elastic moduli of quasi-random spatially irregular hexagonal lattices // Int. J. Eng. Sci. - 2017. - Vol. 119. - P. 142-179. doi: 10.1016/j.ijengsci.2017.06.004
- Pabst W., Uhlířová T., Gregorová E., Wiegmann A. Young’s modulus and thermal conductivity of closed-cell, open-cell and inverse ceramic foams - model-based predictions, cross-property predictions and numerical calculations // J. Eur. Ceram. Soc. - 2018. - Vol. 38. - P. 2570-2578. doi: 10.1016/j.jeurceramsoc.2018.01.019
- Roberts A.P., Garboczi E.J. Elastic moduli of model random three-dimensional closed-cell cellular solids // Acta Mater. - 2001. - Vol. 49, iss. 2. - P. 189-197. doi: 10.1016/S1359-6454(00)00314-1
- Finite element simulation of mechanical behaviour of nickel-based metallic foam structures / S.A. Kaoua, D. Dahmoun, A.E. Belhadj, M. Azzaz // J. Alloys Compd. - 2009. - Vol. 471, iss. 1-2. - P. 147-152. doi: 10.1016/j.jallcom.2008.03.069
- Koudelka P., Jiroušek O., Valach J. Determination of mechanical properties of materials with complex inner structure using microstructural models // Mach Technol Mater. - 2011. - Vol. 1, iss. 3. - P. 39-42. http://mech-ing.com/journal/3-2011.html
- 3-D quantitative image analysis of open-cell nickel foams under tension and compression loading using X-ray microtomography / T. Dillard, F. N’guyen, E. Maire, L. Salvo, S. Forest, Y. Bienvenu [et al.] // Philos. Mag. - 2005. - Vol. 85, iss. 19. - P. 2147-2175. doi: 10.1080/14786430412331331916
- Cristescu N.D., Craciun E.-M., Soós E. Mechanics of elastic composites. - CRC Press, 2003. doi: 10.1201/9780203502815
- Kachanov M., Sevostianov I. Micromechanics of materials, with applications / Serie: Solid Mechanics and its Applications. - Vol. 249. - Springer Int. Publ. AG, 2018. doi: 10.1007/978-3-319-76204-3
- Mills N.J. Finite element models for the viscoelasticity of open-cell polyurethane foam // Cell. Polym. - 2006. - Vol. 25, iss. 5. - P. 293-316. doi: 10.1177/026248930602500502
- Ortona A., Rezaei E. Modeling the properties of cellular ceramics: From foams to lattices and back to foams // Adv. Sci. Tech. - 2014. - Vol. 91. - P. 70-78. doi: 10.4028/www.scientific.net/ast.91.70
- Characterization of the deformation behavior of intermediate porosity interconnected Ti foams using micro-computed tomography and direct finite element modeling / R. Singh, P.D. Lee, T.C. Lindley, C. Kohlhauser, C. Hellmich, M. Bram, T. Imwinkelried, R.J. Dashwood // Acta Biomater. - 2010. - Vol. 6, iss. 6. - P. 2342-2351. doi: 10.1016/j.actbio.2009.11.032
- Zhu H.X., Hobdell J.R., Windle A.H. Effects of cell irregularity on the elastic properties of open-cell foams // Acta Mater. - 2000. - Vol. 48, iss. 20. - P. 4893-4900. doi: 10.1016/S1359-6454(00)00282-2
- Düster A., Sehlhorst H.G., Rank E. Numerical homogenization of heterogeneous and cellular materials utilizing the finite cell method // Comput. Mech. - 2012. - Vol. 50. - P. 413-431. doi: 10.1007/s00466-012-0681-2
- Parvizian J., Düster A., Rank E. Finite cell method - h- and p-extension for embedded domain problems in solid mechanics // Comput. Mech. - 2007. - Vol. 41. - P. 121-133. doi: 10.1007/s00466-007-0173-y
- Krishnan A. The interfacial failure of bonded materials and composites: Dissertation. - Nashville, Tennessee: Vanderbilt University, 2010. - URL: http://hdl.handle.net/1803/14970
- Наседкин А.В., Наседкина А.А., Нассар М.Э. Гомогенизация пористых пьезокомпозитов с экстремальными свойствами на границах пор методом эффективных модулей // Изв. РАН. МТТ. - 2020. - № 6. - С. 82-92. doi: 10.31857/S057232992005013X
- Дерффель К. Статистика в аналитической химии. - М.: Мир, 1994. - 268 с.
- Roberts A.P., Garboczi, E.J. Elastic properties of model porous ceramics // J. Amer. Ceram. Soc. - 2000. - Vol. 83, iss. 12. - P. 3044-3048. doi: 10.1111/j.1151-2916.2000.tb01680.x
- Авдеенко А.М., Крупин Ю.А., Пименова Н.А Ротационные моды деформации пористых структур // Вестник ПНИПУ. Механика. - 2014. - № 3. - С. 5-16. doi: 10.15593/perm.mech/2014.3.01
- Pia G., Delogu F. Mechanical properties of nanoporous Au: From empirical evidence to phenomenological modeling // Metals. - 2015. - Vol. 5, iss. 3. - P. 1665-1694. doi: 10.3390/met5031665
- Наседкин А.В., Корниевский А.С. Конечно-элементное моделирование эффективных свойств анизотропных упругих материалов со случайной наноразмерной пористостью // Вычислительная механика сплошных сред. - 2017. - Т. 10, № 4. - С. 375-387. doi: 10.7242/1999-6691/2017.10.4.29
- Nasedkin A.V., Kornievsky A.S. Finite element homogenization of elastic materials with open porosity at different scale levels // AIP Conf. Proc. -2018. - Vol. 2046, iss. 1. - Article 020064. doi: 10.1063/1.5081584
- Nasedkin A.V., Kornievsky A.S. Numerical investigation of effective moduli of porous elastic material with surface stresses for various structures of porous cells // Wave Dynamics, Mechanics and Physics of Microstructured Metamaterials. Advanced Structured Materials. - Vol. 109. - M.A. Sumbatyan (Ed.) - Springer, Singapore, 2019. - Ch. 15. - P. 217-228. doi: 10.1007/978-3-030-17470-5_15


