Cryptography Using Multiple Two-Dimensional Chaotic Maps

Published Online August 2012 in MECS DOI: 10.5815/ijcnis.2012.08.01

The development of communications and computer technology requires the data to be private and highly secured. This was -and still- a major problem in many fields like banking systems, defense, and computer networks. For this reason, various techniques have been developed to achieve secure and protected data from attackers. This is called cryptography, in which a cryptosystem is developed to convert the original message, plaintext, into ciphertext and be able to recover it back.

Simple nonlinear systems usually have extremely complicated orbits which look completely chaotic. Any orbit of a dynamical system defined by the differential equation dx/dt = F(x) or by the discrete map x n+ 1 = F(x n ) is determined uniquely by the initial condition, x 0 . But very often, nonlinear systems have unstable orbits. In that case, the distance between close points increases exponentially with time. A chaotic map is a map that exhibits some sort of chaotic behavior. Maps may be parameterized by a discrete-time or a continuous-time parameter. Discrete maps usually take the form of iterated functions. Their properties are similar to confusion and diffusion cryptography properties; so they have been used to build good cryptosystems [1-3]. Furthermore, these properties make chaotic cryptosystems robust against statistical attacks.

Two-dimensional chaotic maps are considered and used in this paper, where their behavior is determined by two, instead of one in one-dimensional maps, initial condition variables which change iteratively and randomly according to some map equations and system parameters [4, 5]. The 2-D chaotic maps are used in the proposed cryptosystem in order to utilize the high degree of randomization associated with the two variables that are used in the process of encryption, and hence increase confusion and diffusion of the system.

The rest of the paper is organized as follows. In section II, related work on discrete chaotic cryptography is reviewed. In section III, the proposed cryptosystem is described. Then, in section IV, analysis and experimental evaluation of our approach are provided. Finally, the paper is concluded in section V.

• II.    Related Work

Many researches in the field of using chaotic maps in cryptography have been developed [1-16]. In [2], a cryptosystem, with a symmetric key block cipher, used an external key of variable length (maximum 128-bits) to generate system parameters and initial conditions of the chaotic map. The ciphertext depends on the secret key only; so to make it robust against any reasonable attack, it uses the feedback technique. The main weaknesses in this technique are: The ciphertext depends on the secret key only, so it is vulnerable to known plaintext attack; it is used for small size blocks (8 bits); it is easy to brute-force because the initial condition, X 0 , has only 256 values; and when P i (i^th block of plaintext) and C i (i^th block of ciphertext) are known it is easy to find the range of X ^new which is the last value of the initial condition calculated by iterating the map to be used in ciphertext generation.

In [3], an explanation of the weaknesses of using a 128-bits external key to derive the initial conditions and number of iterations is given. These weaknesses are summarized as follows. For the interval chosen for a system parameter, λ , the small resolution used to calculate it, together with the deterministic nature of the algorithm, allow for a known plaintext attack. Also, the process to derive an initial condition, X, and number of iterations, N , from the external key, K , is fundamentally flawed, allowing for chosen ciphertext and chosen plaintext attacks. Therefore, given the total lack of security along with the low encryption speed encourage us to search for better techniques for secure applications.

In [4], another chaotic map-based technique was proposed, in which multiple one-dimensional chaotic maps are used instead of a one-dimensional chaotic map. This algorithm uses an external secret key of variable length (maximum 128 bits). The plaintext is divided into groups of variable length (number of blocks in each group is different). These groups are encrypted using a randomly chosen chaotic map from a set of chaotic maps.

The number of iterations and initial conditions for the chaotic maps depend on the randomly chosen session key and the previous block of ciphertext. The encryption/decryption process is governed by two dynamic tables, which contain the number of iterations and initial conditions for the chaotic maps; these tables are updated from time to time during the encryption/decryption process. The ciphertext depends on the secret key only; so it is vulnerable to known plaintext attack and also a small block size (8 bits) is used.

In [5], a cryptanalysis technique showed some weaknesses of the previous algorithm, which can be summarized as follows. The cipher generated looks like a block cipher, but it behaves as a stream cipher, and equations of initial conditions and number of iterations are dependent on the secret key only, which results in the initial contents of the two dynamic tables exactly the same for different plaintext sequences as long as the secret key is fixed. The initial condition variable, X , which changes by iterating the maps, is used to update the two tables for encrypting the next plaintext block, and each plaintext block is encrypted with the last value of X . At the end of the paper, they make a straightforward modification to make the value of X dependent on both the key and the plaintext.

In [6], an improved cryptosystem has been proposed to eliminate the essential weaknesses and redundancies of the previous cryptosystems. This scheme uses two skew tent maps instead of a logistic map. The difference between logistic and tent maps is that the logistic map is a polynomial mapping that exhibits some sort of chaotic behavior ( x = rx (1– x )), where r is the system parameter and x 0 is the initial condition, while the tent map is an iterative function, in the shape of a tent, forming a discrete-time dynamical system. It takes a point x on the real line and maps it to another point. The redundant operations are abandoned to simplify the cipher. Permutation within ciphertext was implemented using two independent chaotic variables to mask the plaintext. One-dimensional chaotic map is used, which limits the degree of confusion and diffusion. Also, the number of iterations is calculated using the key indices 60 to 67, i.e. K 60 , K 61 , …, and K 67 are used to provide the number of iterations to be applied to the map, which reduces the range of the expected number of iterations (Maximum number of iterations = 2⁸ = 256).

• III.    Proposed Cryptosystem

The proposed cryptosystem takes the advantages of chaotic maps and reduces drawbacks of cryptosystems discussed in section II. The general characteristics of the approach are:

• •    Use of two-dimensional chaotic maps to increase confusion and diffusion, namely, using four 2-D chaotic maps: Baker's map, Duffing map, Hénon map, and Kaplan-Yorke map. Table I describes the precise mathematical equations of the four maps, where the variables X 0 and Y 0 are initial condition variables and all

of the variables a , b , α , and β are system parameters which control the degree of randomization in maps.

• •    Making the block size variable (8 bits, 32 bits, or 64 bits) to be suitable for any application. For example, in a multimedia application, which needs fast data transfer, a small block size such as 8 bits may be selected .

• •    For the first block, the initial conditions, X 0 and Y 0 , are calculated using the secret key and an Initial Vector, IV , where IV size is equal to block size. For the i^th block, i > 0, X 0 and Y 0 are calculated using the key and the previous cipher block, C i –1 .

• •    Dividing the secret key which is 128 bits into four parts, each 32 bits, to do some operations on them such as swapping and shifting, before being involved in calculations of X 0 and Y 0 .

• •    Making X 0 not dependent on the key only, but involving also the ciphertext to calculate it and making Y 0 dependent on the key.

Table I. Map number, equations, and system parameters of the 2-D maps used in the proposed cryptosystem

N	Map equations	S.P.
0	Xn +1 = an / b an +1 = 2 × an (mod b), 0 ≤ an <  b / 2 or 2 – 2 × an (mod b ), b / 2 ≤ an <  b Y n +1 = Y n / 2, 0 ≤ a n <  b / 2 or 1– Yn /2, b / 2 ≤ an <  b	a 0 = 17 b = 37
1	Xn +1 = Yn Yn +1 = – b × Xn + a × Yn – Yn	a = 17 b = 3
2	X n +1 = Y n – α × X n 2 Y n +1 = – β × X n (mod 81)	α = 5 β = 3
3	Xn +1 = an / b an +1 = a 0 + 2 × a n 2 (mod b ) Y n +1 = α × Y n + cos(4 × π × X n )	α = 0.6 a 0 = 81 b = 7

N : Map number, S.P.: System Parameters, 0: Baker's map, 1: Duffing map, 2: Hénon map, 3: Kaplan-Yorke map

Block diagrams for encryption and decryption of the i^th block are shown in Figs. 1 and 2, respectively. P i and C i are the i^th plaintext and ciphertext blocks, respectively. X 0 i and Y 0 i are the output variables of the initial conditions generation phase to be used in the chaotic map phase for the i^th block, while X _i^new and Y_i^new are the outputs of the chaotic map phase.

• A.    Initial conditions generation phase

Plaintext and ciphertext are structured as:

P = P 1 P 2 P 3 ... P n

C = C 1 C 2 C 3 ... C n

where P i and C i are blocks of 64 bits, 32 bits, or 8 bits. If message length is not an integral multiple of block size, then padding is used. In our system, we pad with the character 'z'. The 128-bits key is divided into four parts, a , b , c and d , each of 32 bits. Three versions of initial conditions generation phase are suggested to accommodate the different block sizes. Fig. 3 describes the steps of generating the initial conditions X and Y using the 128-bits key, and the 64-bits blocks. The following steps are carried out:

• •    Swap the left and right parts of b , i.e., the 16-bits right half becomes the 16-bits left half and vice versa.

• •    Perform a circular shift left (4 bits) for part d .

• •    A = a ⊕ c , B = b' ⊕ d' , Y = A | B , where | is

concatenation.

• •    Divide the 64 bits previous cipher block into two 32 bits blocks, C 1 and C 2 .

• •    W = C 2 ⊕ A , R = C 1 ⊕ B , X = W | R .

Here, swap, circular shift, key and cipher block division are performed to produce random values of X and Y and hence increase confusion and diffusion. Figs. 4 and 5 show the steps of generating the initial conditions for 32-bits and 8-bits block sizes, respectively.

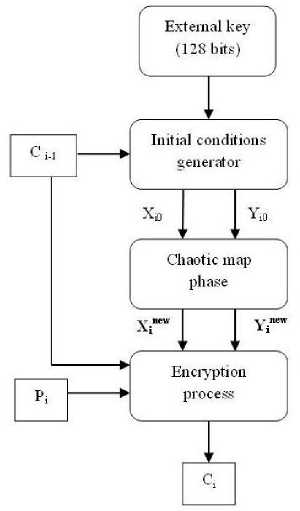
Figure 1. Encryption process

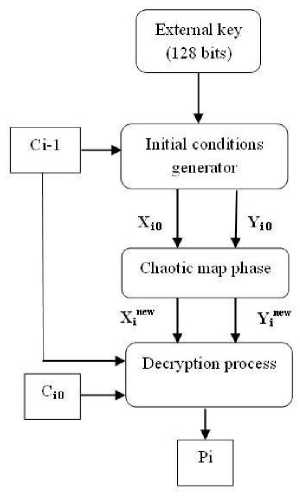
Figure 2. Decryption process

• B.    Chaotic map phase

In this phase, the values of X and Y , resulting from the initial conditions phase, are used to calculate the index, N , of the chaotic map to be used for the current block, the number of iterations, IT , to be performed on that map, and the values X^new and Y^new .

N = Y mod 4

X mod 23

IT = <  X mod 7

X mod 3

if N = 0, 3

if N = 1

if N = 2

Experiments showed that if chaotic map No. 0, 1, 2, or 3 iterates for more than 23, 7, 3, or 23 iterations, respectively, the values of X^new and Y^new reach zero. To avoid this, and to take advantage of the chaotic map randomization, the values 23, 7, and 3 are chosen to be the modulus. X^new , and Y^new are calculated iteratively as follows:

For i = 1 to IT

(Xnew, Ynew) = mapN(X, Y ), where mapN(X, Y ) is calculated by applying the Nth map substituting the values of X and Y from the previous phase. Table I demonstrates map indices, corresponding equations, and typical values of parameters (can be changed). The chaotic map phase is illustrated in Fig. 6.

Cipher block, each part is 32 bits Key , each part is 32 bits

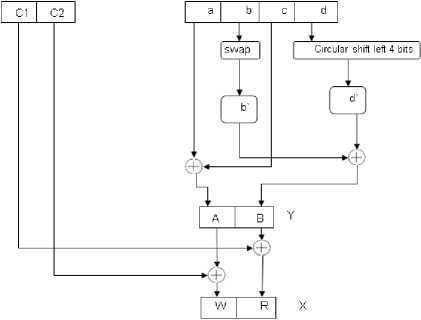
Figure 3. Initial conditions generation for 64-bits blocks

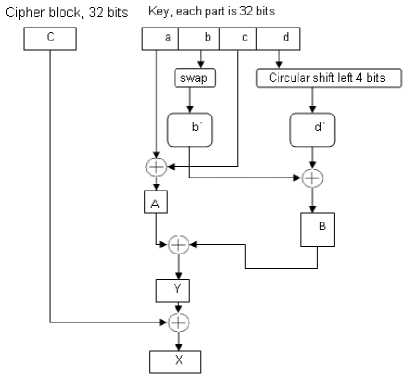
Figure 4. Initial conditions generation for 32 bits blocks

• C.    Encryption/decryption phase

The values X^new and Y^new , calculated in the previous phase, are used in the encryption/decryption as follows:

C i = P i + X^new + ( Y^new × C i –1 )                        (5)

P i = C i – X^new – ( Y^new × C i –1 )                        (6)

Note that dealing with the values of P i , X^new , Y^new , and C i –1 as decimal values, normal operations: addition (+), multiplication (×), and subtraction (–) are used. The proof that decryption is the inverse of encryption is:

P i = C i – X^new – ( Y^new × C i –1 ) = P i + X^new +

( Y^new × C i –1 ) – X^new – ( Y^new × C i –1 ) = P i       (7)

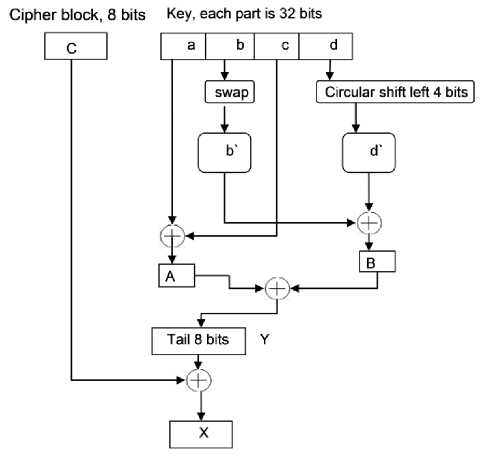
Figure 5. Initial conditions generation for 8 bits blocks

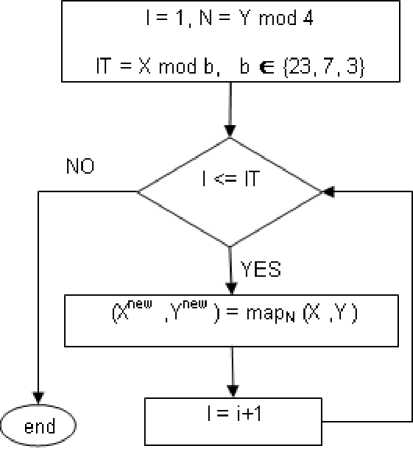
Figure 6. Chaotic map phase

• IV.    Analysis and Experimentation

Our cryptosystem has improvements from several aspects:

• (a)    The diffusion and confusion are increased due to:

• •    Using two-dimensional chaotic maps which have random behaviors,

• •    Involving the ciphertext in the initial conditions generation phase, and

• •    Involving the ciphertext in the encryption/decryption phase.

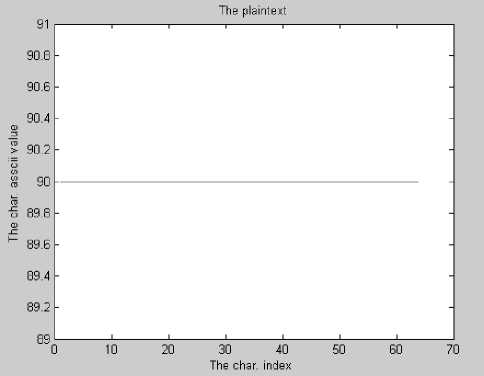
(a)

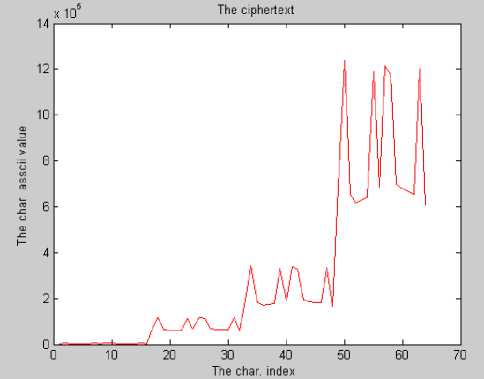
(b)

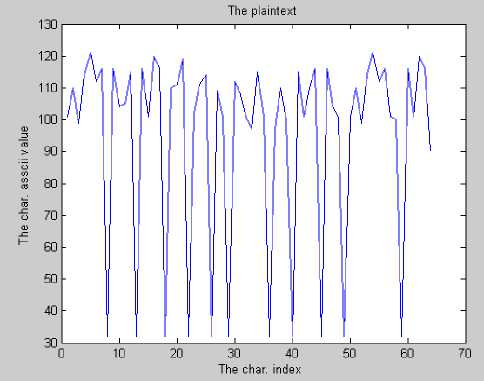
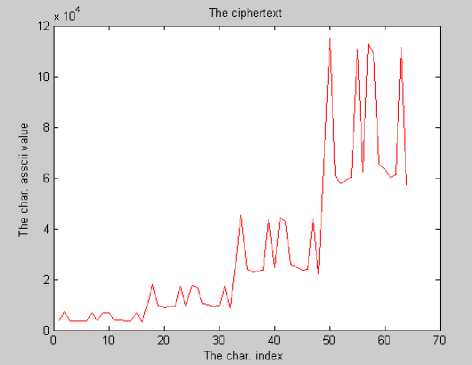
Figure 7. (a) constant sequence plaintext, and (b) corresponding ciphertext

In Fig. 7(a), the plaintext is a sequence of the same character, while the resulting ciphertext shown in Fig. 7(b) hides the constancy of plaintext, thus guaranteeing the diffusion property. Moreover, encrypting the plaintext shown in Fig. 8(a) using a key of zeros results in the ciphertext shown in Fig. 8(b) demonstrating that ciphertext randomization is preserved. Experiments showed that even if the same key used in encryption is used in decryption with one bit difference, the recovered plaintext is totally different from the original. The ciphertext shown in Fig. 9(a) is the encryption of the plaintext in Fig. 8(a) using some key value. If decryption is done using the same key changing the first bit, obtained plaintext is shown in Fig. 9(b). Changing the last bit of the key will result in the plaintext shown in Fig. 9(c).

• (b)    The key size has been increased in order to increase the range of keys, so that more security is achieved (key size = 128 bits => 2¹²⁸ keys), and hence the system is secure against brute-force attack.

• (c)    For each block, X and Y are dynamically created, and their values change iteratively in spite of using the same key, because we involved the ciphertext in their generation.

because he has three unknown variables: X , Y , and C i –1 and one equation: P i – C i = X^new – ( Y^new × C i –1 ). Also, the range of variables X and Y is not determined due to the randomness of the chaotic maps.

• (g)    Even if the adversary got X^new and Y^new , he cannot recover the key, because X^new and Y^new are outputs of the chaotic map phase, which is a one way non-invertible function.

  

  (a)

  
  
  

  (a)

  
  
  

  (b)

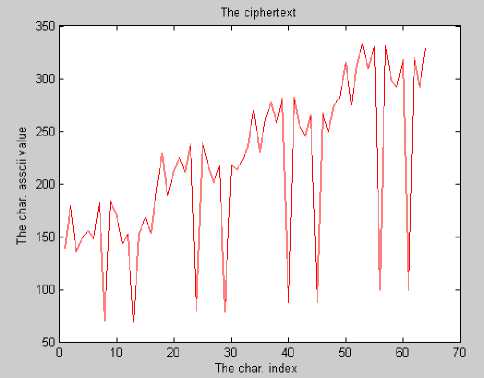
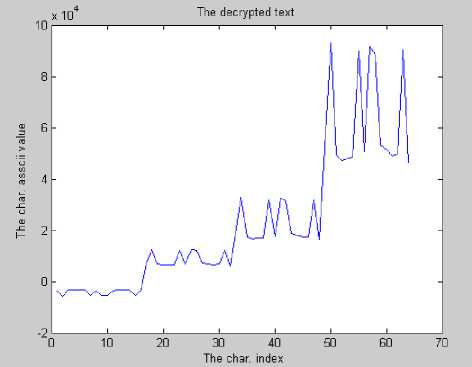
  Figure 8. (a) plaintext, and (b) ciphertext using a key of all zeros

  
  
  

  (b)

  
  

  • (d)    The proposed cryptosystem is proved to be secure against ciphertext-only attack. If the adversary could get one cipher block C i , he will not be able to find the corresponding plaintext block P i , because X , Y , and C i –1 are still unknowns. Also, if he could get a cipher block pair C i and C i –1, he will not be able to find P i too, because X and Y are still unknowns, as it is clear from Equation (6).

  • (e)    The proposed cryptosystem is secure against statistical attack due to diffusion and confusion. It is clear from Fig. 7 that even if the plaintext consists of the same repeated character, the pattern is totally hidden in the ciphertext.

  • (f)    The system is also secure against known plaintext attack, e.g., if the adversary can get a cipher block C i and the corresponding plaintext block P i , he will not be able to find the value of X and Y in order to get the key,

  
  
  

  (c)

  Figure 9. (a) ciphertext obtained by encrypting plaintext of Figure 8(a), (b) decrypted text by changing 1 ^st bit of the key, and (c) decrypted text by changing last bit of the key

  
  

• (h)    Finally, the proposed cryptosystem is secure against chosen plaintext attack and chosen ciphertext attack, because there is no plaintext or ciphertext that has special effects, i.e., observed patterns, that can be analyzed to get the key.

The proposed cryptosystem has been implemented using Matlab and simulation results were observed on a 2.0 GHz PC with 512 MB RAM. Tables II and III briefly show the encryption/decryption processing time for different file sizes and types for the proposed cryptosystem and other cryptosystem, respectively. Comparing the proposed system to previous systems demonstrates the enormous difference in processing time, thus leading to a much faster cryptosystem, e.g., the encryption time for a text file of size 90KB, using the 32 bits block size, is 0.219 seconds, while for the improved cryptosystem of reference [6], which is the fastest among the related works mentioned in section II, is 0.6 seconds. Notice that results of previous works, Table III, are taken from [6], where the experiments were implemented on a similar platform like ours: a 2.0 GHz PC with 512MB RAM.

Table II. Encryption/decryption time (in seconds) for different sizes and types of files of the proposed cryptosystem

File type	Plaintext size, KB	Ciphertext size, KB	8 bits System	32 bits System	64 bits System
Plain text file (*.txt)	30	30	0.094	0.094	0.125
	90	90	0.094	0.219	0.328
	240	240	0.250	0.468	0.906
MS Word file (*.doc)	30	30	0.062	0.109	0.140
	90	90	0.125	0.188	0.437
	240	240	0.328	0.484	0.844

Table III. Encryption/decryption time (in seconds) for different sizes and types of files of other cryptosystems

File type	Plaintext size, KB	Ciphertext size, KB	Improved Ref[6]	Multi-one dimensional Ref [4]	Chaotic Ref [2]
Plain text file (*.txt)	30	30	0.19	0.21	1.81
	90	90	0.60	0.62	5.48
	240	240	1.62	1.71	15.55
MS Word file (*.doc)	30	30	0.15	0.19	1.81
	90	90	0.45	0.66	5.46
	240	240	1.32	1.64	14.55

• V.    Conclusion

In this paper, a cryptosystem has been proposed using multiple two-dimensional chaotic maps, where four random behavior chaotic maps were used. The use of these maps as well as the multiple phases of the system apparently increases the degree of confusion and diffusion properties with respect to the plaintext and the key. Computer simulations indicated that the system can produce ciphertext with random distribution irrespective of the value of the key or plaintext. Security analysis and experiments proved that the proposed cryptosystem resists different types of attacks. This robustness is due to involvement of ciphertext in both the initial conditions generation and the encryption/decryption processes; hence, a secure approach is produced. Furthermore, the proposed cryptosystem verified its superiority to previous related systems in terms of speed, i.e., it is distinguished by much less computation time leading to a faster, as well as more secure, and promising cryptosystem to be used in different applications.

Acknowledgment

We thank anonymous referees for their constructive comments.