Cuckoo Search Algorithm using Lèvy Flight: A Review

Published Online December 2013 in MECS

At present, problem solving optimization algorithms are met heuristics and all of them are nature inspired. As soon as they are emanated, they are accepted by researchers and applied widely. Ant Algorithms were inspired from the behavior of ants in the wild. Particle Swarm Optimizations (PSO) was stimulated from the world of fish and bird, whereas the Firefly Algorithm was influenced by the flashing patterns of tropical fireflies. All of these bio-inspired met heuristic algorithms are being applied in problem solving optimization such as NP-Hard problems: the Travelling Sales Man Problem (TSP). The strength of all modern met heuristic algorithms are the fact that they mimic the best properties in nature , particularly biological systems emerged from natural selection over millions of years , of them two important features can be simulated numerically or algorithmically into two major features : intensification, and diversification. Intensification tries to search around the current best solutions and select the best candidates or solutions, whereas diversification utilizes the search space of the algorithm efficiently. CS algorithm revolves around the behavior of obligatory brood parasitism of some species of cuckoo as well as the Levy Flights (after the name of French mathematician Paul Pierre Levy) of some birds and fruit flies which follow the random walk of heavy tailed probability distribution step size. These observations are formulated into algorithms and implemented as a novel and new idea. CS is compared with other already existing popular optimization algorithms in connection with numerous optimization problems.

Cuckoo Hashing is another computing technique for resolving hash collisions of values in hash functions in a table. It derives the concept from some cuckoo species chicks pushing out of the nests other eggs or chicks at the time of hatching. The idea was derived from Ramses Pugh and Fleming Fiche Rodler in 2001. Since hybridization is possible between the above mentioned algorithms, as a result we can say that CS is derived from Swarm Intelligence. By statistical analysis it has been established that problem solving success of CS is far superior to PSO (PSO2007)[1]. Modified CS (MCS) is also made by Walton et al [2]. It delivers high convergence rate which out performs other optimizers. Basically it performs massively at high dimension bench mark objective functions. Consequently it can be applied on engineering problems. To be precise, the modification stresses on the information exchange between two best eggs or best solutions.

The paper is mainly organized according to the paragraphs as: i) Study of cuckoo behavior and Levy flight, ii) The primary concept behind the Cuckoo search with pseudo code, iii) Realization and mathematical results using different test functions, and iv)Comparative study between PSO and GA. Finally in conclusion it has been shown that less number of parameters (two in the given study) of the CS algorithm leads to its better efficiency. In future more complex parametric study can be carried out with more promising results in terms of the aim of speed of convergence. As a result of this the computational cost reduces.

• II.    OBSERVATION ON CUCKOO BEHAVIOR AND LÈVY FLIGHTS

• A.    Obligatory Brood Parasitism of Cucko

The first impressions about cuckoos are their beautiful tone. But apart from their sound, they have a spectacular intrusion reproductive strategy. This is known as brood parasitism. There are two types of brood parasitism: non-obligatory and obligatory. In non-obligatory brood parasitism, cuckoo lays eggs in the nest of conspecifics (i.e., same species) and in their own nests as well. Examples: Bank Swallows, African Weavers. In obligatory brood parasitism cuckoos lay eggs in the nest of hetero-specifies, and do not require building the nest of their own and incubate the eggs. Examples: Brown- Headed Cowbirds and European Cuckoos. It has been reported that 1% of all bird species follow obligatory brood parasitism. Example: all African Honey Guides, almost half of the species of cuckoos, the Black Headed Duck in South America, Shiny Cowbirds, Screaming Cowbirds, Bronze Cowbirds and Giant Cowbirds. There are three types of brood parasitism: intraspecific brood parasitism, cooperative breeding, and nest takeover. Sometimes the host birds engage in fight with intruder cuckoos. Either the host birds may throw out the eggs if they find the eggs of invaders or may leave the nest and rebuild the nest elsewhere. The female cuckoos of the New World brood parasitic Tapera who are expert to imitate the colour and shape of the eggs of chosen host species, as a result of which, the probability of their eggs to be relinquished declines and intensifies their reproductively. The time of egg-laying of some parasitic cuckoo is also astonishing. Parasitic cuckoo lays eggs on the nest of host birds. Host bird incubates both the eggs of its own as well as the eggs of parasitic cuckoos. It is also amazing that the parasitic eggs hatch slightly earlier than that of the host eggs. Host birds incubate parasitic chicks as their own. By natural instinct, cuckoo chicks try to evict the host eggs randomly out of the nest for the sake of its own existence and food. By investigation, it has been found that cuckoo chicken imitate the sound of host chicken to obtain more food from the host mother.

• B.    Concept of Levy Flights

A Levy Flight can be thought of as a random walk where the step size has a Levy tailed probability distribution. The name Levy Flight came after the French mathematician Paul Pierre Levy. The term Levy Flight was coined by Benoit Mandelbrot who used specific definition of the distribution of the step sizes. Eventually Levy Flight term has been using to refer discrete grid rather than continuous space. It is a Markov Process. Exponential property of Levy Flight gives it a scale invariant property and they are used to model data for exhibiting/ showing clusters. In nature many animals and insects follow the properties of Levy Flight. Recent studies of Reynolds and Frye demonstrate that fruit flies or drosophila melanogaster covers the skies by using numerous series of straight flight paths/ routes followed by a sudden right angle turn which is a Levy-flight-style intermittent scale free search pattern. Hunter-gatherer forage pattern exhibit the typical feathers of Levy Flight, observed by Ju/’bonsai on human behavior. Studies also show that light rays follow Levy Flights in optical material [3]. Ultimately, it is being used in optimization search and significant results are emerging.

• III.    THE BASIC IDEA BEHIND CUCKOO SEARCH

Cuckoo Search (CS) is a new met heuristic search algorithm. It is characterized by three laws: each cuckoo lays one egg at a time and disposes the egg at a randomly chosen host nest, secondly the best nest with excellent quality of eggs will carry over to the next generation, and lastly the number of host nest is fixed and the probability of parasitic egg-discovery by the host bird is p_a ∈ [0, 1]. The host bird can either throw out the parasitic egg or forfeit that nest for a better new nest. For practicality, in the later hypothesis it can be assumed that fraction p a of the nests are substituted by new nests (with new random solutions).In one form of fitness the quality or fitness of a solution is proposed to be proportional to the value of the objective function in case of a maximization problem. Other form of fitness can be proposed in the same manner as that of fitness function of GAs. In a simple manner of representation, each egg in a nest is represented by a solution and each cuckoo egg symbolizes a new solution. The aim is to exploit the new and probably finer/ superior solutions (cuckoos) to substitute a not-so good solution in the nests. More intricate cases like multiple eggs in a nest, symbolizing a set of solution, can be incorporated in this algorithm. Here the simplest approach, i.e., one egg in one nest, has been applied. Guided by the above three rules, the CS is abridged by the pseudo code:

Cuckoo Search via Le'vy Flights begin

Objective function f(x), x=(x 1 , x 2 ,………x d )^r Generate initial population of

A host nests x i (i=1, 2, 3……, n)

While (l < Maxgeneration) or (stop criterion )

Get a cuckoo randomly by Le v y Flights Evaluate its quality/fitness F i

Choose a nest among n (say, j) randomly if (F i > F j ),

Replace j by the new solution;

end

A function (p a ) of worse nests

Are abandoned and new ones are built;

Keep the best solutions

(or nests with quality solutions);

Rank the solutions and find the current best end while

Postprocess results and visualization end

A new solution is symbolized by x (t+1) and a cuckoo is represented by i, then a Levy Flight is carried out by

x ^(t+г) = x® + а ф Le’vy (A),                 (1)

Where α > 0 is the step size which is adjusted according to the scale of the problem of interests. In most of the cases α is assumed to be unity. Equation 1 represents the stochastic equation of random walk. Generally random walk is charecterised by Markov chain where the next state is represented by the present location (the first term of the above equation) and the transition probability (the second term). EX-OR symbolizes exclusive OR i.e., entry wise multiplication. This entry wise multiplication is equivalent as that of PSO, except that the random walk via Le v y Flight is more efficient in exploring / acquiring the search space because its much longer step size increases exponentially in the last stage. Le v y Flight is a random walk with the random step size following a Le vy distribution.

Le ’ vy ~ u = I~ ²,  (1 < A < 3),                (2)

Le v y distribution has infinite variance with infinite mean with a power-law step size of a heavy tail as it is shown in fig 1.

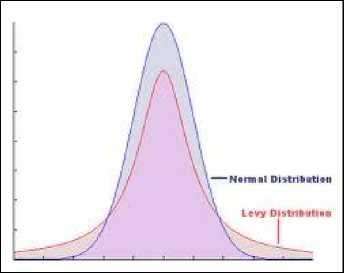
Figure 1. Le v y and Normal Distribution [4]

Using Levy walk, few new solutions must be explored for the speed up of local search from the best solutions so far. It should be kept in mind as a warning that the system must not be trapped in a local optimum. For this reason, a portion or adequate amount of fraction of the new solutions must be cropped up from far field randomization with locations far enough from the current best solution. At a glance, both CS and hillclimbing in combination with few large scale randomizations appeared to be similar, but there is some salient dissimilarity. Firstly, like GAs and PSO, CS is a population based algorithm, at the same time it explores some kind of elitism and/or selection as that of harmony search. Secondly, the randomization is more efficient as the step size is heavy tailed with any possible large step size. Thirdly, the number of tuning parameters is less than GAs and PSO which in turn promises to be acceptable to a wider class of optimization problems. Moreover, an individual nest representing a solution makes CS adaptable to the class of Meta population algorithms.

• IV.    REALISATION AND NUMERICAL VERIFICATION

• A. Authentication and Specification Studies

After implementation, the algorithm has to be verified using test functions with analytical or known solutions. In this case, the bi-variate Michaelwicz function is used.

f (x,y) = - sin(x) s i n^{2 m} (^-) - sin(y) sin^{2 m} (^~)

Where m=10 and (x, y) Є [0, 5] × [0, 5] with global minima f * 1.8013- ≈ڏ at (2.20319, 1.57049) .

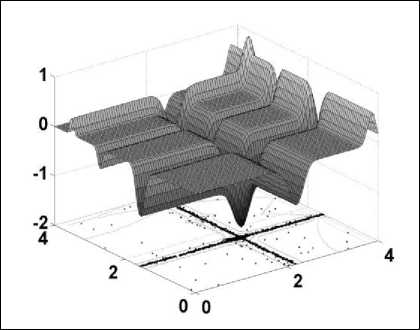
Figure 2. The landscape of bi-variate Michaelwicz Function [5]

The landscape of this function is shown in fig 2. CS finds these global optima easily and it is shown in fig. 3. With final locations of the nests marked ◊. Here, the number of nests, step size and probability of parasitic egg-discovery used are n=15, α = 1 and pa = 0.25. In most of the simulation cases n=15 to 50. The results from the figure show that most of the nests accumulate towards the global optimum as the optimum is approaching. In case of multimodal functions, the nests are scattered at different local optima. From the above discussion, it is clear if the numbers of nests are higher than that of the number of local optima, the CS scans all the optima simultaneously. In case of multimodal and multiobjective optimization problems, this advantage may be more pronounced. In this particular case, the number of host nests (i.e., the population size n) and the probability p_a are varied where n=5,10,15,20,50,100,150,250,500 and p a = 0,0.01,0.05,0.1,0.15,0.2,0.25,0.4,0.5.Simulation result shows that n=15 and p_a =0.25 are adequate for majority of the optimization problems. From the results and analysis, it has been deduced that the rate of convergence mostly is independent of the parameters used, which in turn leads to inessentiality of fine adjustment for any problems. Therefore, throughout the given problem, n=15 and p a = 0.25 has been used.

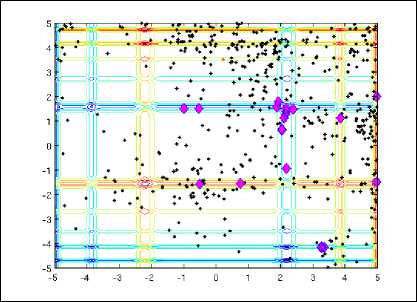
Figure 3. Search paths of nests in Cuckoo Search where the final location of the nests are denoted by ◊ in the figure [6]

Where a single global minima f * =0 at x * =(0,0,-----,0)

for all -600 ≤ x i ≤ 600 where i=1,2,---,d.

5) Ackley’s Function is multimodal

/( X )=

-20 ехр

-0․2

-

exp

[¹ ∑cos(2 Ttx_t )]

+(20+ е ),

B. Test Functions

There are numerous benchmark test functions to verify the performance of optimization algorithms. All new optimization algorithms must be validated and tested against these benchmark functions. In this algorithm (CS), few test functions have been utilized for simulations.

Where a global minima f * = 0 at x *    = (0,0,---,0)

between -32.768 ≤ x i ≤ 32.768 with i=1,2,----,d.

6) Generalized Rosen rock’s Function

d-1

f ( X )= ∑[(1- Xi )²

1=1

+ 100( X_i+1

^- Xi )²],

• 1)    Sphere Function-De Jong’s first function

d

f ( X )= ∑ Xi ,

1=1

X_t ∈ [-5,12,5,12],

Where global minimum f* =0at x* = (0, 0, -----, 0) with d dimension.

• 2)    Easom’s Test Function is unimodal

f ( X , У ) =-cos( x ) cos( У ) exp[-( x - я )²– ( У -

К )²],                                                     (5)

Where

Where a minima f(x*) = 0 at x* = (1, 1, ---, 1).

• 7)    Sahwefel’s Test Function is multimodal

d

f(X) ∑*-Xi sin (√| Xi|)+,-500≤Xi ≤ 500,(11)

i=l

Where a global minima f * = -418.9829d at x i ^* = 420.9687

with i=1, 2, d.

• 8)    Rastrigin’s Test Function

f(X)+ 10d+ ∑t=i [ xt - -10cos(21lXi)],(12)

( X , У ) е [-100,100] х [-100,100],                   (6)

With global minimum of f* = -1 at (Π, Π) in a very small region.

• 3)    Shubert’s Bivariate Function

Where a global minima f * =0 at x * =(0,0,---0) in a hypercube -5.12 ≤ x i ≤ 5.12 with i=1,2,---,d.

9) Michalewicz’s Test Function It has d! local optima

/( X , У )

- ∑ i cos[( i +

1=1

+ 1)],

1) X +1]∑

1=1

cos[(i+1) У

f ( X )= -∑ sin ( Xi )[ sin ( "5 )]  ,( m = 10), (13)

i=l

With 0 ≤ x i ≤ Π and i=1, 2, ---, d. The global minima is f * ≈ -1.801 for d=2, whereas f * ≈ -4.6877 for d=5.

Where 18 global minimas exists in the region (x,y) ∈ [10,10] x [-10,10]. The global minimas have a value of -186.7309.

• 4)    Griewangh’s Test Function

This function has many local minimas.

f ⁽*)= ₄₀¹₀₀ ∑^х‘ – ∏ cos (_√ I ⁾

1=1      1=1

+1 ,

C. Comparative Study of CS with PSO and GA

According to the recent research, PSO algorithms left behind GAs and other traditional algorithms for many optimization problems. This is because of the attributes in the broadcasting ability of the current best estimates which promise better and quicker convergence of optimality. It is here been shown the performance of CS versus that of PSO and GAs using most of the standard test functions. The algorithms were run more than hundred times for implementation of Matlab simulation to get meaningful statistical interpretation. The algorithms stop for the variation function values which are less than threshold tolerance ε ≤ 10-5. The Table 1 shows the results when the global optimas are reached. The format of the table is: average number of evaluations (success rate), i.e., 3221± 519(100%) indicate the average number (mean) of the function evaluation is 3221 with standard deviation 519. The success rate of searching for the global optima for this algorithm is 100%. It is also clear that CS is far more efficient in searching the global optima with the highest (100%) success rate. These evaluation processes of each test function are practically instantaneous with a 3 GHz desktop (personal) computer performing 10,000 evaluations in 5 seconds. For all the aforesaid test functions, CS has outperformed both GAs and PSO. The main reasons are: excellent balance between randomisation and intensification with few number of control parameters.

An efficient metaheuristic algorithm is specified by a good balance between intensive local search strategy and an efficient exploration of the whole search space. Moreover, there are only two search parameters in this algorithm; the population size n and p a. Once n is fixed, p a primarily supervi\ses the elitism and in turn controls between the randomization and local search. Due to involvement of two parameters the CS algorithm becomes less complex and hence more fundamental. After original CS, there are few new researches that have come out with more complex parameters taking into account. More marvelous results are generated ending up with the aim of speed of convergence.

TABLE I. COMPARISON OF CS WITH GENETIC ALGORITHMS

Algor ithms /Func tionss	Multiple Peaks	Michalew iez’s (d=16)	Rosenbr ock’s (d=16)	De Jong’s (d=256)	Schwefe l’s (d=128)	Ackley ’s (d=128 )	Rastrigi n’s	Easom’s	Griewan k’s	Shubert ’s (18 minima)
	52124±	89325±	55732±	25412±	227329	32720±	110523	19239±	70925±	54077±
GA	3277	7914	8901	1237	±7572	3327	±5199	3307	7652	4997
	(98%)	(95%)	(90%)	(100%)	(95%)	(90%)	(77%)	(92%)	(90%)	(89%)
	3719±	6922±	32756±	17040±	14522±	23407±	79491±	17273±	55970±	23992±
PSO	205	537	5325	1123(10	1275	4325	3715	2929	4223	37557
	(97%)	(98%)	(98%)	0%)	(97%)	(92%)	(90%)	(90%)	(92%)	(92%)
	927±	3221±	5923±	4971±	8829±	4936±	10354±	6751±	10912±	9770±
CS	105	519	1937	754	625	903	3755	1902	4050	3592
	(100%)	(100%)	(100%)	(100%)	(100%)	(100%)	(100%)	(100%)	(100%)	(100%)

• V. CONCLUSION