D2D Communication Using Distributive Deep Learning with Coot Bird Optimization Algorithm

With the growth of wireless devices, cellular systems face an excessive task to satisfy the users’ difficulties like interaction in communications, lagging in receiving and sending large files and so on. These difficulties lead to a focus on D2D communication to improve the spectral efficiency and performance of the wireless system. D2D communication is a technique that is utilized to handle the increase in mobile traffic by improving the spectrum utilization of the cellular networks and thus improving the overall performance and throughput. D2D communication uses mobile devices to exchange data through the direct link without routing via the Base Station (BS). So it is getting more attractive to network operators nowadays [1]. D2D users can transmit and receive the signal under the control of the node B (eNB) base stations, allowing unburdening of the traffic. It is important in communication technology with resource management and power allocation. While sharing the spectrum between the cellular user (CU) and D2D user (DU), there is some joint interference. By identifying lots of issues in D2D communication, there are numerous types of research have been conducted using deep learning techniques.

D2D communication using deep learning is the most efficient method so it is used in various models. By using a deep neural network with a distributed allocation of D2D communication, the device has the ability to choose the transaction control for the data not getting support from eNB [2]. D2D can individually choose its transmission rate, it sorts this network as topologically extensible [3]. The transmission power of D2D user equipment (DUE) to maximize the rate without causing interference to the Cellular User Equipment (CUE) is allocated using resource allocation [4]. The power allocation for D2D communication using immediate wireless info and power transmission is used to develop pricing strategies [5]. The D2D operation is non-transparent to the user and happens in cellular frequencies [6].

The existing methods for D2D communication are based on different algorithms some of which are whale optimization algorithm (WOA), Honey Badger Optimization (HBO), Flamingo Search Optimization (FSO), and Particle Swarm Optimization (PSO). The drawback of the above mention algorithms is slow convergence, low accuracy and so on.

To overcome these issues, D2D communication using distributed deep learning [7] with Coot Optimization Algorithm (COA) which minimizes the Bit Error Rate (BER) has been proposed.

The proposed method uses a distributive deep learning technique to develop the power allocation scheme for D2D communication which decreases the involvement of eNB to achieve the optimal cell throughput. After gaining the enhanced power value, the deep learning is used to confirm the efficiency of a whole system in an autonomous mode.

The main contribution of the proposed paper is included below:

• •    To develop a power allocation scheme for D2D communication with maximum throughput and minimum BER. We use the distributive deep learning method by maintaining the quality of service.

• •    Distributive deep learning has been used to train the network and is found to improve the model to get the autonomous resource allocation and power value.

• •    The coot bird optimization algorithm is used to achieve the optimized minimum BER value, which leads to enhancing the performance of the deep learning technique.

• •    After attaining the optimized values, the distributive deep learning architecture is used to test the efficiency in autonomous mode.

• •    The proposed model confirms independent resource allocation with optimal power rate and least BER value for D2D communication.

2.    Related Works 3.    Proposed Methodology 3.1.    System Model

In D2D communication, there are several studies combined with different techniques to give enhanced outcomes. Some of the works done by different authors in D2D communications are explained here. The paper proposed by Abrardo, Andrea et al [8] used dedicated and reuse modes to implement D2D communications. The dedicated mode exploits the available radio resources and the reuse mode used the same channel for one or more users within each cell. This method convergence the local maxima of the objective function slower. Pham, Quoc-Viet et al [9] proposed WOA to get the optimized resource allocation problem. The result shows 200 realizations for each plot and the users are positioned in each realization and also provide the adaptation of WOA of potential resource allocation problems in 5G wireless network.

Authors Pandey, Krishna and Rajeev Arya [11] proposed D2D communication using ML to maximize the QoS constraints with power control and used the optimization method which minimizes the BER value and to solve the MINLP non-convex problem is solved by the iterative approach of resource allocation with power control. The result of this paper gives a higher system capacity than the normal iterative algorithm. The paper by Zhi, Yuan, et al [12] focused on D2D communication using reinforcement learning in heterogeneous cellular networks. The result shows the increase in sum rate below the quality of service constriction to enable the mm-wave and cellular bands in the heterogeneous cellular networks. The paper by Dan Wang et al [13] explained D2D communication using reinforcement learning. It is used to select the available channel and power for the user which is used to maximize the system capacity. Authors Lee, Woongsup et al [14] proposed D2D communication using a deep learning technique. This paper solved the complex iterative problem in an iterative manner and the result revealed that the Weighted Sum Rate (WSR) is increased with low computation time. Han, Shuai [15] studied the spectrum allocation in the underlaying cellular network using multi-agent reinforcement learning. To select the resources and achieve power control for each user, Q-learning has been used. The result shows a higher throughput in terms of performance.

In D2D communication systems, it is possible to balance reducing power consumption with maintaining reliable communication by designing the cost function for power constraints choice. The cost function may be set up to balance the data rate that the D2D connections are capable of transmitting while using a minimal amount of energy. For MultipleInput Multiple-Output Non-Orthogonal Multiple Access (MIMO-NOMA) systems, Zhang et al. [22] employs the Lagrange function to optimise power allocation while satiating user fairness requirements. To the objective function, the Lagrange function is utilised to add a penalty term that measures how much the user fairness requirement has been violated. The approach is proven to achieve near-optimal energy efficiency while meeting the user fairness criterion by using the Lagrange multiplier to change the power allocation depending on the user fairness constraint. For device-to-device (D2D) communications subject to quality-of-service (QoS) restrictions, Liu et al. [23] provide a power allocation method. Under the restrictions of the minimum data rate need for each D2D connection and the maximum transmit power of each D2D transmitter, the power allocation goal is to maximise the overall system throughput. The maximum power that the transmitters may utilise in this suggested D2D communication system is frequently constrained, which might have an impact on the performance of the entire system. The optimization of the power allocation scheme in D2D communication systems can be formulated as a constrained optimization problem, where the objective function is employed to maximize the system performance while satisfying the power constraints.

To increase spectral efficiency, the CU and DU share the cellular spectrum. Fig.1 represents the D2D communication model which contains BS, CUE and DUE. For cellular users, orthogonal resource allocation is used, which implies that the number of subcarriers in the network is equal to the number of cellular users. Thus, the cellular network is supposed to use Orthogonal Frequency Division Multiplexing Access (OFDMA).

D2D User

Fig.1. System model

It has DUE users and CUE users with a set of D2D device pairs M = {0,1,2,3,.....m} and the set of OFDMA channels N = {0,1,2,3,4......n}. The received signal Y_n , _k , _kis shown in equation (1)

Y n,m,m = H n,m,m S n,m,m + ∑ i ∈ ℳ,i≠m H n,i,m S n,i,m + W n,m,m

The complex channel gain among the receiver and transmitter m is denoted as Hn,m,m . The receiver of the D2D device pair is represented as Hn,i,m. Sn,m,m is denoted as a symbol of transmission. An additive noise with variance is represented as Wn,m,m then i represent the pair of D2D transmitters. The spectral efficiency tm is expressed in equation (2)

_{tm(pm) =∑n ∈ Nlog2}(_{1 +}        (H n,m,m ) ² ₂ p n,m      ₂ )

∑ i ∈ ℳ,i≠m (H n,i,m ) p n,i +(σ n,m )

max∑ m ∈ ℳ t m (p m ) (3)

Subject to,

∑ n ∈ N p m ≤ p max ,

ℳ ∈ m

∑ m ∈ ℳ (H n,m,m ) p k ≤ Q max ,

n ∈ N

Where power restriction is given as pmax. The interference constraints of the per channel are given as Qmax . It performs to control the total power that should not exceed pmax.

The throughput value of each pair is not increased autonomously so Distributive Deep Learning is used to train a model to maximize the sum of throughput. Then for optimizing the values Coot bird optimization is used which also enhances the performance of distributed deep learning.

• 3.2.    Coot Optimization

• 3.3.    Distributive Deep Learning with Coot Optimization Algorithm

Coot bird optimization algorithm is used to enhance the performance of the deep learning technique and also provide the optimization value. The algorithm is constructed on the habits of the coot bird. The collection of the coot is called a swarm. It is mainly used to optimize the values and enhance the distributive deep learning technique. This proposed D2D communication needs an optimized maximum throughput value and minimum BER value for the efficient model. The algorithm starts with an initial random population, ( ⃗ x ⃗ ) = { ⃗ x ⃗ ₁, ⃗ x ⃗ ₂, ….. ⃗ x ⃗ _n} represented as an objective function and the objective value is written as ( ⃗ o ⃗ ) = { ⃗ o ⃗ ₁, ⃗ o ⃗ ₂, ….. ⃗ x ⃗ _n}. To improve the optimization techniques there are a set of rules. Since there is no assurance of getting the solution in a single run, optimization techniques use the finest number of optimal problems. So, more iterations are taken to find the optimal probability. Random movement in the both side, chain movement, group leaders leading movement, group leading towards the optimal area are randomly performed to achieve the global best solutions using equation (23).

Distributed deep learning technique uses the location of the D2D device as input. It needs input data and labels for successful performance. The system does not know the proven solution before the resource and power allocation. The cost function from Equation (13) is used as an objective function instead of the labels from the optimal result. Hence it can generate input data for every iteration. It is mainly used to increase the training efficiency of the model. Deep learning needs the sum of throughput to improve the model. The Sum of throughput can be calculated by collecting an inferred transmission power of each device during the training period. Using the location information of a transmitter and a receiver, the model can determine the transmit power automatically and it is used to increase the rate of transmission by the device by sustaining the inference constraints.

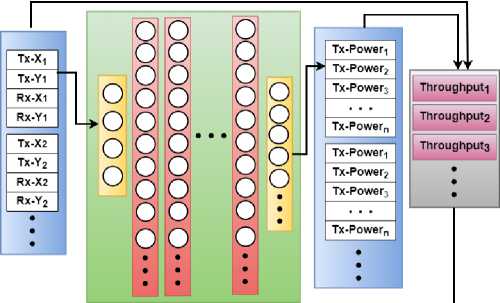
To maximum sum of throughput

Fig.2. Architecture of distributed deep learning

The proposed distributed decision scheme can maximize the total D2D rate in the multi-cell environment while maintaining interference constraints. Resource allocation is utilized to reduce the co-channel interference and power distribution to reduce inference constraints. The proposed model is trained to exploit the throughput value because the throughput value does not maximize independently for each pair as shown in Fig. 2. Parameter is defined as θ and the rule for the D2D pair m is θm. The optimal set θ∗m is shown in equation (6).

θ ^{̅ ∗} m = argmax∑ m ∈ ℳ,θ _m ∈ θ̅ _mt m (p m (θ m ))                                  (6)

θ ^̅ _m

Where the capacity of transmission is the resultant of the procedure θm is denoted as (pm(θm)). By this, each device in a similar set ℳ has the same θm as shown in equation (7).

θ^∗_ℳ = argmax∑ m ∈ ℳ, t m (p m (θ)) θ

Where θ∗ℳ is the same as θm and it depends on a specific ℳ. Likewise, the result of the θ∗ℳ is the approximate result of the θ∗m expressed in equation (8).

∑ m ∈ ℳ t m (p m (θ ℳ )) ≲ ∑ m ∈ ℳ,θ ^∗ _m ∈ θ ^̅∗ _m

t m (p m (θ^∗ m ))

θ^∗_ℳ ̅ = argmax∑ m ∈ ℳ̅ ∑ m ∈ ℳ t m (p m (θ))

θ

∑

m ∈ ℳ ^̅

∑ m ∈ ℳ t m

(p m (θ^∗ ℳ̅ )) ≲ ∑

ℳ ∈ ℳ ^̅

∑ m ∈ ℳ,θ ^∗ _m ∈ θ ^̅∗ _m

^tm ( ^pm^{(θ ∗} m⁾ )

To find the optimal result of θ^∗_m , it is difficult to approximate the value θ^∗ ̅ . So deep learning is adopted. Transmit power p can be determined by the neural network based on θ. The power transmitter p is expressed in equation (11)

p_m(θ^∗_ℳ ̅ ) = (m, θ^∗_ℳ ̅ )

The cost function of power constraints uses the Lagrange function. Therefore, throughput is directly used in distributive deep learning itself. A throughput and restrictions are non-convex problems. The sum of D2D communications transmits power is under the threshold p_max, η_p . The cost function of interference to eNB is also the same as power constraints and it is defined after defining the constraints formula. e is an eNB, e ∈ E and ReLU is a Rectified linear Unit function. This formula is used to calculate the transmitter on the eNB. Hence the noises are removed. Then, the interference to eNB is defined as λ_if and can be formulated in equation (12)

₌                           I 1      ReLU(Q n,m,e (p m )-p max) \ |

η if (p m ) = ∑ m ∈ ℳ ∑ e ∈ E ∑ n ∈ N log 2 (1 + (       ^{n,m,e m max} ))                        (12)

The cost function is denoted as C which is expressed in equation (13)

C(P m )     ^ meM t m⁽ P m ) + ^ ifⁿif^(pm ) + ^ p ⁿp^(pm )                             ⁽¹³⁾

Where λif, λpare the Lagrange multiplier. They have a similar form to objective and ReLU in cost function C so it can be easy to find the appropriate value.

Coot optimization is used to enhance the deep learning technique. The location is obtained by an equation (14).

Cootpos(i) = rand(1, d). ∗ (ub - lb) + lb

lb ={lb 1 , lb 2 …. lb n }                                                  (15)

ub = {ub1,ub2….ubn}                                           (16)

After creating the starting residents to determine the location of the mediator an objective function O_i = f( ⃗ x ⃗ ) is used to calculate an optimized value.

A movement of this side and that side is implemented using the random position which is formulated in equation (17).

Q = rand(1, d). ∗ (ub - lb) + lb                                     (17)

This movement will travel in different spaces which leads the algorithm to trap in local optima. The new randomly moving both the side locations are calculated using equation (18).

cootPos(i) = CootPos(i) + A × R2 × (Q - CootPos(i))

Where R2 is the random number and A is calculated as in equation (19).

A=1-L×(It1er)                                (19)

Where the current iteration is represented as L and Iter is represented as the maximum iteration.

The next movement is the chain movement. To implement the chain movement, first, the distance between the two coots and their position is identified. The new and initial location of the coot is formulated in equation (20). Where (Cootpos(i - 1) shows the position of the second coot.

Cootpos(i) = 0.5 × (Cootpos(i - 1) + CootPos(i))

The coot has to change its place depending on the leader and it causes early convergence to take the average position. Equation (21) shows how this position is identified.

K= 1 +(i MOD NL)

Where the index of the existing coot is denoted as i and NL indicates the number of leaders then k indicates the index quantity of the leader. The coot should update its position based on the leader. The next location of the coot, according to the new leader is calculated by equation (22)

CootPos(i) = LeaderPos(k) + 2 × R1 × cos (2Rπ) × (LeaderPos(k) - Coot pos(i))         (22)

Where the present location is represented as CootPos(i) and the new leadership position is represented asLeaderPos(k), random number is represented as R1 in the interval [0, 1] then R in the interval [-1, 1]. The value of π is 3.4.

Now the leaders should guide the group to the optimal point. To reach the optimal area the leader should change their position it implemented in equation (23). This equation provides a better way to reach the globally optimized area.

⎪⎧B × R3 × cos(2Rπ) × (gBest - LeaderPos(i)) = gBest

⎫ R4 < 0.5 ⎪

⎬

R4 ≥ 0.5 ⎭

B × R3 × cos(2Rπ) ×

(gBest - LeaderPos(i)) - gBest

Where gBest is the best position of the leader and B is calculated using equation (24).

B=2-L×(¹) Iter

Because of the larger random movement, the algorithm can be avoided from the local optimum. L is the present iteration, Iter is an extreme iteration, and cos(2Rπ) searches around in a different radius to get a best position.

The objective function of the coot bird is to minimize the BER value of the D2D communication and improve the performance of training. Using their signal constraint each user contains the optimal power value and allocates dissimilar frequency bands for the use of communication with the use of threshold value. After the completion of training, distributed deep learning is used with the devices in the cell. For the evaluation, the D2D users are randomly put into the cell. When the BER and power values are gained, the resource allocation will complete itself without disconnecting from the network.

4.    Results

This section includes parameter settings that explain the parameter name and its value considered. Convergence curve shows the convergence for optimization methods. The system performance expresses the comparison between the existing methods and the proposed method. Statistical analysis and accuracy provide the statistical values and accuracy of the proposed and existing methods.

• 4.1.    Parameters Settings

• 4.2.    Convergence

The parameters are tabulated in a Table 1. Cell radius is 600m. The maximum distance of the D2D pair is about 100 m. The value of carrier frequency is 6 GHZ and the standard deviation for the shadowing of effect 8dB is described by a log-normal distribution. The noise is about -174dBm/Hz, and the transmission power constraint is assigned to be 0.75w.

Channel reduction is conveyed by the loss of path with distance. The loss of path exponent is 4 and the loss path of constant is 10 ^-2 . The number of cells is 3, the number of sub-channels is 10 and the quantity of D2D pairs in a cell is 10. This imitation is implemented using Google Colab with python programming.

Table 1. Parameter settings

Names	Assigned values
Cell radius	600m
Maximum distance of D2D pair	100m
Carrier frequency	6GHz
SD for shadowing effect	8dB
Power of noise	-174 dBm/Hz
Transmission power	0.75w
Loss of path exponent	4
Loss of path constant	10-2
The number of cells	3
The number of sub-channels	10
The number of D2D pairs in a cell	10

Fig. 3 illustrates the convergence which is a plot of fitness value versus iteration and gives a comparison between the proposed method and existing methods like Honey Badger Algorithm (HBO), Flamingo Search Optimization (FSA), and Particle Swarm Optimization algorithm (PSO).

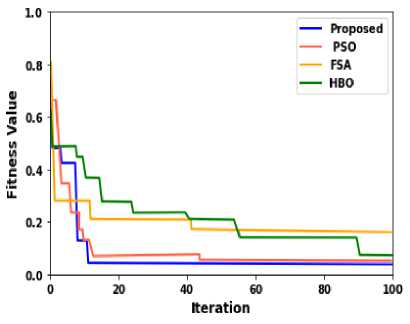
Fig.3. Convergence curve

• 4.3.    System Performance

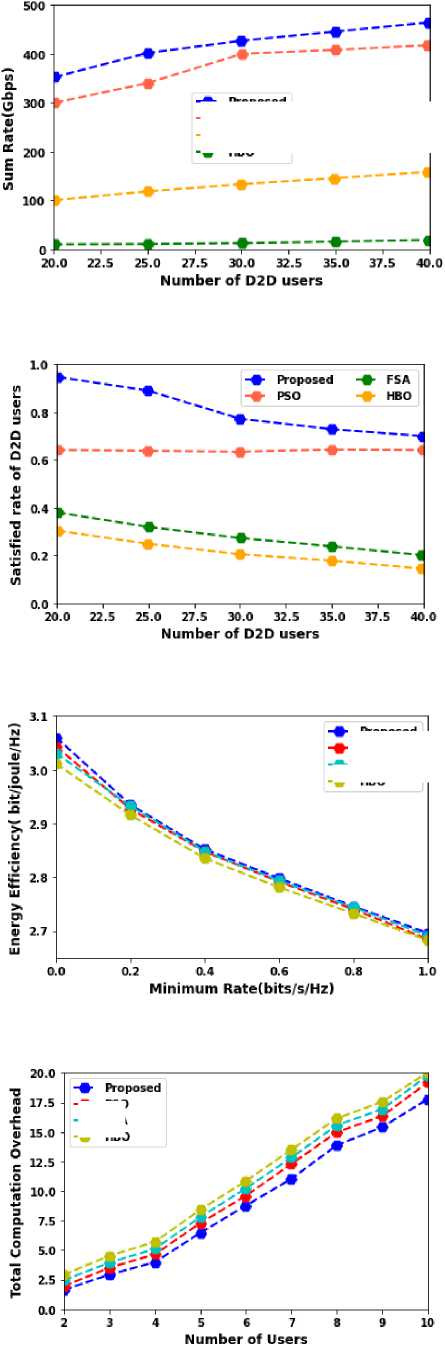
Fig. 4 show the sum rate of the system compared with the surviving models with different users. The graph shows the present model gives the greatest performance compared to other existing methods like HBO, PSO, and FSA. The HBO model gives the least performance among the existing methods in D2D communication. The proposed model shows that it maintains the QoS requirement of D2D communication. Fig. 5 illustrates the satisfied rate of different D2D users. From the graph, it can be seen that the proposed work gives the best rate of performance 94% compared to other existing algorithms implying that the proposed method satisfies the maximum QoS of the user requirements. To manage user interference, the proposed algorithm adjusts the channel and communication mode of the D2D user.

In Fig. 6 EE rate is compared with the existing algorithm. Fig. 7 is a plot of the total computation overhead in terms of bit/joule/Hz. The proposed method shows the coot optimization algorithm gives a lower computation overhead of up to 2.7 bit/joule/Hz which is due to the limitation in the number of subcarriers. The system-wide computation overhead and percentage of unloading can be increased by increasing the user.

Fig.4. Sum rate

Fig.5. Satisfied rate

Fig.6. Energy efficiency

Fig.7. Computational overhead

Proposed -e- pso

FSA HBO

Proposed PSO -• FSA -e hbo

-#■ PS о

-e- FSA

-e hbo

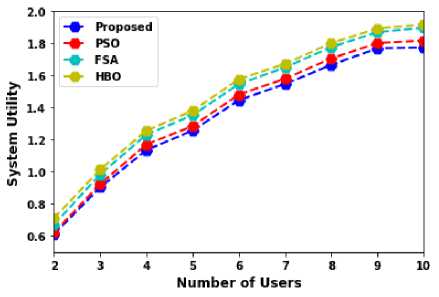
Fig.8. System utility

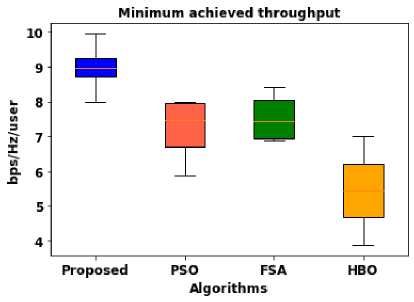
Fig.9. Throughput

• 4.4.    Statistical Analysis and Accuracy

5.    Conclusions

The statistical results are described in Fig. 10, which includes the fitness value of the best, worst, mean and average performance of the proposed algorithm, HBO algorithm, FSA algorithm, and PSO algorithm. From the graph it is clear that the proposed algorithm gives high best, worst, mean and STD values compared with the other models.

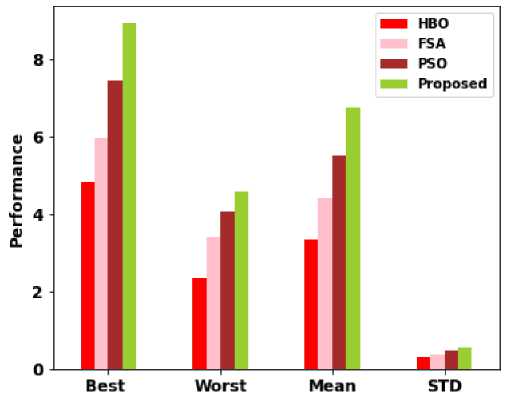
Fig.10. Comparison of fitness values

The accuracy of the proposed method is tabulated in Table 2. The number of D2D devices improves by increasing the accuracy of the proposed method. Which demonstrates the improvement of optimization algorithms. When using 50 devices it gives low accuracy but when we use 500000 devices it gives an accuracy of 99.34%.

Table 2. Accuracy level

K(No. of devices)	Accuracy
50	70.17
500	91.72
5000	97.71
50000	98.62
500000	99.34

A D2D communication model with high power allocation and resource allocation using distributed deep learning and the Coot Optimization algorithm has been proposed. It gives high throughput and QoS with minimum BER without the interference of eNB. Also, the D2D communication model works autonomously resulting in every device attaining near-optimal spectral efficiency. The model is trained as a group with different D2D users with the deep learning technique, in which the values are optimized using the COA and its efficiency has been proved. The proposed method was compared with the existing methods like HBO, FSA, and PSO and it is clear that the proposed method outperforms well in all the iterations compared to other algorithms giving an 80% best value, 41% worst value, 60% mean value and 0.55 STD fitness value with an accuracy of 99.34%.

The Coot inspired regular and irregular global movements search of this algorithm in terms of exploration and exploitation are used to attain optimized power value and the least Bit Error Rate. The Coot optimization can be used as benchmark algorithm to analyse the performance comparisons of remaining unexplored applications in wireless and communication networks. In addition, the results obtained from this simulation will be considered as a dataset for our next extended work as real time implementation to allocate the independent resources with optimized power value and the least Bit Error Rate in D2D communication networks.

Acknowledgment

I confirm that all authors listed on the title page have contributed significantly to the work, have read the manuscript, attest to the validity and legitimacy of the data and its interpretation, and agree to its submission.