Контроль формы оптических волновых фронтов методом Гартмана [1] и его разновидностью – методом Шэка–Гартмана [2] – является в настоящее время одним из наиболее простых и вместе с тем точных и эффективных средств. Аппаратное различие между этими методами состоит, как известно, в использовании лишь различных масок, устанавливаемых перед фотодетектором, выполненным в виде многоэлементной фоточувствительной матрицы: в классических датчиках Гартмана маски представляют собой матрицы (или растры) отверстий малого размера в непрозрачном экране, а в датчиках Шэка–Гартмана маски выполняются в виде матриц микролинз с квадратной или круглой апертурами. К достоинствам датчиков Шэка–Гартмана по отношению к датчикам Гартмана следует отнести, прежде всего, их предельно высокую световую эффективность, а также возможность реализации более плотной дифракционно-ограниченной упаковки микролинзовых элементов и достижения более высокого пространственного разрешения при однократной выборке оптического сигнала. Между тем для ряда приложений (включая мощные лазеры [3]) высокая световая эффективность масок датчиков Шэка–Гартмана не представляет интереса. С другой стороны, важными преимуществами датчиков Гартмана перед датчиками Шэка–Гартмана являются их более высокая точность вследствие повышенной точности контроля центроидов сфокусированных световых точек [4], более высокая степень локализации выборок элементов волнового фронта [5] и отсутствие ошибок, вызванных дефектами и неодинаковостью характеристик микролинзовых элементов [6]. Несмотря на то, что большая часть погрешности от несовершенства микролинзовых элементов может быть устранена при калибровке датчика, полного избавления от такой погрешности осуществить не удаётся. Это объясняется тем, что карта поправок для компенсации различия аберраций микролинзовых элементов, получаемая при калибровке датчика для эталонного волнового фронта (плоского либо сферического), в общем случае отличается от карт поправок, необходимых для компенсации указанных аберраций при измерении неизвестного волнового фронта [7]. Такая особенность датчиков Гартмана позволяет существенно снизить их остаточную инструментальную погрешность и достичь сверхвысокой точности и чувствительности при измерении волновых фронтов [8]. Кроме того, вышеотмеченная повышенная степень локализации выборок элементов волнового фронта [5] делает возможным достижение повышенного разрешения при детектировании волнового фронта путём дополнительных поперечно-смещённых микровыборок волнового фронта при его сканировании в пределах однотипных субэлементов боксов по площади рабочей апертуры (то есть в пределах участков вокруг сфокусированных световых пятен на фотосенсоре). Другой вариант «вырожденного» датчика Гартмана с одиночным приёмным элементом (одним отверстием) и сканированием в пределах всего поля рабочей апертуры описан в работе [9].

Отметим, что одним из общих ограничений в методах Гартмана и Шэка–Гартмана с их классическими реализациями является ограничение на минимальные размеры апертуры элементов масок и, соответственно, ограничение на предельно реализуемую разрешающую способность и остаточные погрешности от перекрёстных помех между оптическими каналами. Данные ограничения обусловлены, в первую очередь, дифракционными факторами и зависят от размеров и формы функции рассеяния точки отдельных апертур масок. При резко ограниченной форме апертур масок Гартмана либо микролинзовых элементов масок Шэка–Гарт-мана возникают эффекты оконтуривания световых пятен на фотосенсоре в виде паразитных дифракционных колец. Для частичного подавления уровня интенсивности данных колец, как известно, может быть использован метод сглаживания резких переходов в распределениях пропускания по полю апертур маски, называемый методом аподизации.

Настоящая работа посвящена развитию метода Гартмана в части оптимизации и физической реализации новых типов масок на основе многоэлементных амплитудных масок с аподизированными апертурами с целью улучшения качества восстановления волнового фронта. Применительно к методу Гартмана мы проведём сравнение оптических характеристик амплитудных масок с резко ограниченными границами отверстий и полутоновых амплитудных масок, формирующих световые пятна на фотосенсоре в виде плавных быстрозатухающих функций. В рамках настоящей работы мы будем называть указанные распределения функциями рассеяния. В настоящей работе рассматриваются вопросы оптимизации параметров бинарных и аподизированных масок Гартмана, сравнение их характеристик, а также вопросы физической реализации аподизированных масок в виде тонких хромовых плёнок с плавным изменением пропускания. На данный момент авторам настоящей работы не известны аналогичные публикации на эту тему.

падении интенсивности до уровня 10 %, rвы(Cхir2c) , при- ближённо можно представить в виде суммы радиуса этих отверстий rвх и поправки на дифракционное уширение порядка 0,861 V%z , то есть

r (Circ) вых2

r (Circ) вх

+ 0,861 V% z .

Для общего случая резко ограниченных круглых отверстий произвольного радиуса r _вы ^(C _х ^irc) , как было установлено, хорошо применима эмпирическая формула

г ^(Clrc) = /Г r^(Clrc) 1 2 Г r^(Clrc) 1 2

* вых |_ * вых 1 J ⁺ |_ * вых 2 J

,,.,_) ,2 0,3721 % 2 z²

Г 'вх 1 + ТгТ

+ 1,722 V% zr^ c + 0,7413 % z

На рис. 1 показаны графики функций, построенные по уравнениям (1)–(3) при фиксированных значениях рабочего расстояния между маской Гартмана и фотосенсором, z =2 мм, а также длины волны используемого излучения, % =532 нм.

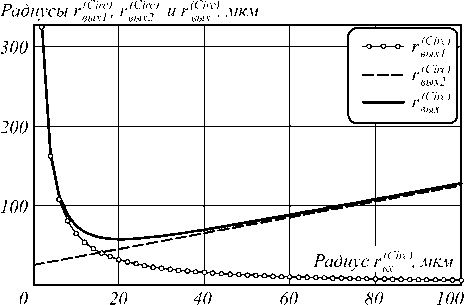
Рис. 1. Графики функций, связывающих радиусы резко ограниченных, хорошо изолированных, круглых входных отверстий в маске Гартмана и радиусы выходных пучков на фотосенсоре

Из них видно, что результирующая функция rв(ыCхirc) [rв(хCirc)] имеет некоторый минимум, который можно вычислить из (3) методом итераций либо решая соответствующее уравнение четвёртой степени. Выбирая серию выборок с различными радиусами отверстий маски rвх(Circ) , обеспечивающих получение функций рассеяния с радиусами, близкими к указанному минимуму, и вычисляя серию распределений интенсивности функций рассеяния Iв(ыCхirc) , методом итераций можно найти уточнённую оптимальную функцию рассеяния Iв(ыCхirc) , которая будет иметь минимальный радиус rв(ыCхirc) по за- данному уровню интенсивности. Величину радиуса отверстия маски r0(Circ) для найденной оптимальной функ- цию рассеяния можно принять в качестве оптимальной для бинарной маски Гартмана, поскольку она обеспечивает возможность уменьшения поперечных размеров боксов на маске Гартмана, а также даёт возможность повысить оптическое разрешение и снизить перекрест- ные помехи между оптическими каналами. С помощью указанной процедуры было найдено, что оптимальный радиус отверстия r0(Circ) с минимальной функцией рассеяния при z=2 мм и %=532 нм составляет 25,4 мкм.

Для иллюстрации вариаций масштаба и формы профилей интенсивности функций рассеяния Iв(ыCхirc) на рис. 2 сплошными линиями показаны графики этих функций для трёх размеров отверстий, равных соответственно половине от оптимального   (а)– r„Г) = 0,5 r0(Circ) = 12,7 мкм,   оптимальному(б) - r„(Circ) = r0(Circ) = 25,4 мкм и удвоенному оптимальному (в) — r (Circ) = 2 rn(Circ) = 50,8 мкм. вх0

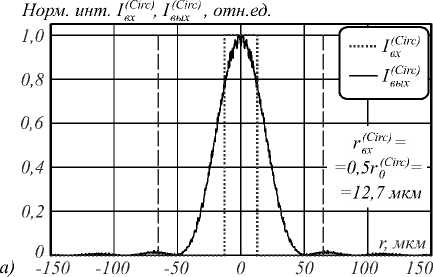
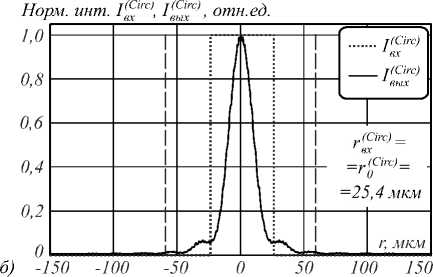
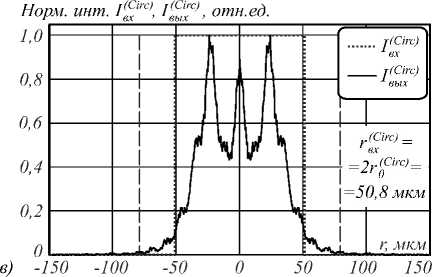
Рис. 2. Зависимости распределения входных и выходных световых интенсивностей для бинарной (а–в) и полутоновой (г) масок Гартмана (с одиночным отверстием)

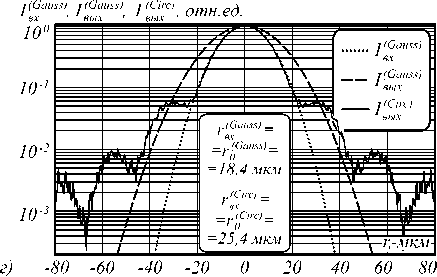
Линиями в виде точек показаны соответствующие распределения интенсивности I _в ⁽ _х ^Circ) непосредственно за маской. Нами был использован стандартный скалярный метод расчёта светового поля через угловой спектр плоских волн [10]. Для удобства сопоставления на рис. 2 а – в представлены также соответствующие функции пропускания отверстий, показанные линиями в виде точек. Как можно видеть, затухание функций рассеяния является относительно медленным (особенно при рассмотрении опускаемых здесь графиков, построенных в полулогарифмическом масштабе). Кроме того, для большей информативности на рис. 2 а – в пунктирными линиями обозначены границы пучков, определённые по приближённой аналитической формуле (3). Сравнение графиков распределения интенсивностей непосредственно за маской и на выбранном расстоянии z для отверстия оптимального размера (рис. 2 б ) показывает, что поперечный размер функции рассеяния по уровню 0,5 (FWHM) составляет 21,25/50,95 = 0,42 от размера отверстия маски. Это указывает на то, что при выбранном соотношении величин % , z и r ₀ ^(CiIc) наблюдается линзовый (фокусирующий) эффект.

В качестве второго исследованного в данной работе типа масок была выбрана полутоновая маска с аподизи-рованным Гауссовым профилем пропускания круглых отверстий T (r) = exp{-2r2 / - rGuss) ] }, где r„(Guss) -радиус пропускания отверстий по уровню exp(–2). Если осветить такую маску (с одиночным отверстием) плоской волной, то на её выходе будет имитироваться фундаментальный Гауссов пучок с комплексной амплитудой A (r) = exp (-kr2 / 2 (Z + iz)) / (1 + iz / Z), где k = 2п/%, а Z = k [r„(xGauss)] / 2 - расстояние Рэлея. При этом интенсивность пучка в произвольной плоскости z будет изменяться по закону

• --I A 42- ’ -2⁽ Z 2^)J-     -

• а радиус rв(ыGхauss) будет изменяться как

(Gauss) (Gauss) ²          2      2 (Gauss) ²

• Гвых   = - Гвх    J + 4 z k - Гвх    J =

  производной ∂ r_в⁽_ы^G_х^auss) /∂r_в⁽_х^Gauss)позволяет определить нам оптимальный радиус пучка в перетяжке, который для заданной длины волны λ и на заданном расстоянии z обеспечивает минимальную величину радиуса r_вы^(G_х^auss)пучка:

  r₀(Gauss) _{= λ}z /π .                                         (6)

  При данном размере расстояние z оказывается равным расстоянию Рэлея Z для пучка, интенсивность которого описывается уравнением (4) и который образуется на выходе маски. При этом размер пучка на расстоянии z = Z увеличивается в V2 раз. В соответствии с формулой (6) при z =2 мм и λ =532 нм оптимальный радиус отверстия составляет r₀^(Gauss)= 18,4 мкм . Для иллюстрации на рис. 2г в полулогарифмическом масштабе показаны графики изменения интенсивности пучка непосредственно за маской [ I_в⁽_х^Gauss)(r) ] и на расстоянии z = 2 мм [ I_в⁽_ы^G_х^auss)(r) ], рассчитанные по уравнению (4) и нормированные до единичного уровня. Для удобства сопоставления на этом же рисунке в новом масштабе приведён график распределения интенсивности функции рассеяния I_в⁽_ы^C_х^irc)(r) для оптимального неаподизированного круглого отверстия с (Circ) радиусом r₀^(Circ).

  Сравнение графиков функции рассеяния I_в⁽_ы^C_х^irc)(r) от оптимального круглого отверстия с радиусом r₀^(Circ)= 25,4 мкм и распределения интенсивности I_в⁽_х^Gauss)(r) за маской с Гауссовым пропусканием при оптимальном радиусе отверстия r₀^(Gauss)= 18,4 мкм наглядно демонстрирует интересный факт: в пределах широкого центрального участка (при 0 ≤ r< 22 мкм) указанные распределения практически совпадают, и график I_в⁽_ы^C_х^irc)(r) в данных пределах можно описать Гауссовой функцией. Таким образом, здесь мы демонстрируем, что в данном режиме круглое отверстие с бинарным пропусканием можно рассматривать не только как микролинзу, но и как простейший преобразователь дискового распределения интенсивности в Гауссово. Эта демонстрация делается, насколько нам известно, впервые и может быть полезной для различных приложений. Для приводимого примера числовая апертура сфокусированного псевдогауссового пучка с радиусом перетяжки r₀^(Gauss)от отверстия с бинарным пропусканием равна NA = λ / [πr₀^(Gauss)] = 0,01 при достаточно малом числе Френеля N_F =[r₀^(Circ)] ²/(λz)= 0,61 . При этом плоскость рабочего расстояния z =2 мм находится за плоскостью последнего максимума интенсивности на оси, z_макс=[r₀^(Circ)] ²/λ = 1,21 мм, при падении интенсивности пучка на оси до уровня 66,4% относительно уровня последнего максимума. Указанное преобразование дискового распределения в Гауссово даёт возможность провести аппроксимацию псевдогауссового

  
  

  распределения Гауссовым. При этом оптимальный размер радиуса резко ограниченного круглого отверстия, обеспечивающего минимальный размер светового отклика на расстоянии z, приближённо можно определить аналитической формулой

  r0 ^≈7 2λz /π . (7)

  Между тем сравнение графиков I_в⁽_ы^G_х^auss)(r) и I_в⁽_ы^C_х^irc)(r) на рис. 2г показывает, что в периферийной области r > 31,5 мкм график I_в⁽_ы^C_х^irc)(r) демонстрирует большую интенсивность, чем I_в⁽_ы^G_х^auss)(r) , начиная с уровня интенсивности 5,4%.

  По уровню падения интенсивности до 0,1 % (приближённо по уровню одного бита интенсивности света, регистрируемого фотосенсором с 10-разрядным АЦП) полный размер функции рассеяния (FWHM) для маски с Гауссовым пропусканием составляет 48,4 мкм. Соответствующий размер для маски с бинарным дисковым пропусканием равен 65,6 мкм, то есть в 1,36 раза больше.

  Если мы примем за единицу уровень относительной световой энергии ε⁽₀^Circ), собираемой в пределах «жёсткого» отверстия с оптимальным радиусом r₀^(Circ), то уровень световой энергии на выходе «мягкого» Гауссового отверстия с оптимальным радиусом r₀^(Gauss), отнесённый к энергии на выходе отверстия с указанным радиусом r₀^(Circ), будет выражаться как

  
  

  ε

  
  

  (Gauss) 0

  
  

  2π_∫^∞I_в(_хGauss)

  
  

  (r)r dr

  
  

  ( Gauss)     (Gauss )

  r_вх     =r₀

  
  
  
  

  2π∫₀^∞Iв⁽х^Circ)(r)rdr

  0 ^вх                      (Circ) (Circ)

  r_вх    = r₀

  
  

  .

  
  
  
  

  То есть интегральное пропускание света «мягкой» маской с отверстием радиуса r₀^(Gauss)будет вчетверо меньше пропускания «жёсткой» маски с отверстием радиуса r₀^(Circ). Это обстоятельство указывает на то, что «мягкие» маски способны осуществлять более локализованную энергетическую выборку светового поля и обеспечивать таким образом более высокую разрешающую способность при сканирующем методе контроля волнового фронта [5]. Имея выигрыш по существенно более высокой концентрации света в центральной (приосевой) области, «жёсткие» маски проигрывают «мягким» маскам по степени рассеяния света в периферийной области.

  Таким образом, мы продемонстрировали превосходство аподизированных масок для использования в тестах Гартмана, и последующая часть работы посвящена разработке технологии синтеза именно таких масок с шагом между отдельными отверстиями, P = 176 мкм, существенно большим, чем вышеуказанный полный размер функции рассеяния (176>>48,4), и согласованным с параметрами фотосенсорной матрицы. При указанном шаге P расстояние Тальбота, на ко-

  
  
2.    Изготовление полутоновой хромовой маски

тором происходит первое самовоспроизведение структуры маски, составляет Z T =2 P ²/ λ = 116,5 мм, что в 58 раз превышает рабочее расстояние z =2 мм (эквивалентное в данном случае расстоянию Рэлея Z для Гауссовой структуры отверстий маски). Это способствует малому уровню перекрёстных помех между оптическими каналами [11] .

Полутоновая маска (ПМ) представляет собой оптическую подложку с тонким слоем поглощающего вещества, коэффициент пропускания которого плавно меняется по заданному закону. Реализация ПМ в плёнках металла с контролируемым прецизионным изменением пропускающей способности представляет к настоящему времени большие сложности. Вместе с тем разработка технологий изготовления таких масок может оказаться полезной для целого ряда приложений.

В настоящей работе использован новый метод изготовления ПМ в плёнках хрома, основанный на плавном, нелинейном, компьютерно-контролируемом изменении мощности лазерного излучения в зависимости от требуемой плотности структуры ПМ, а также на последующем селективном химическом травлении. При данном методе используется эффект модификации структуры плёнок хрома под действием лазерного излучения, а также эффект изменения скорости растворения модифицированных плёнок хрома в селективном травителе в зависимости от дозы лазерного облучения.

Согласно классической модели [12], термическое воздействие лазерного излучения на тонкие плёнки хрома приводит к наращиванию тонкого слоя окисла, изменяющего физико-химические свойства облучённой поверхности. Также было установлено [13], что, кроме образования на поверхности плёнки окиси хрома, протекает ещё ряд процессов: в частности, отжиг, рекристаллизация и частичное окисление плёнки на всю толщину [14].

Установлено, что в зависимости от величины экспозиции время полного стравливания плёнок отличается в несколько раз, а наклон кривой изменения пропускания становится существенно более пологим. На рис. 3 приведены основные этапы предложенного метода изготовления ПМ.

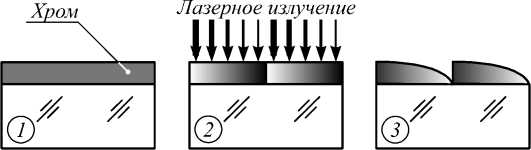
Рис. 3. Лазерный термохимический метод изготовления ПМ. Этап 1: нанесение плёнки хрома; этап 2: экспонирование движущимся лазерным пучком; этап 3: проявление в селективном травителе вание осуществлялось на установке CLWS-300IAE сфокусированным лазерным пучком (0,6 мкм FWHM, λ =532 нм) при непрерывном вращении фотошаблона (12 об./с) и радиальном перемещении пучка с шагом 0,5 мкм. Мощность экспонирующего излучения управлялась по заданной программе от компьютера.

Размер области записи ПМ – 12×12 мм. ПМ представляла собой прямоугольный растр из 64×64 одинаковых апертур с Гауссовым пропусканием и шагом 176×176 мкм. Указанное число апертур и их шаг согласовывались с размером и числом пикселов фото-сенсорной матрицы: в боксе 176×176 мкм умещалось 32×32 пиксела фотоматрицы (размером 5,5×5,5 мкм). Диаметр каждой полутоновой апертуры – 38 мкм на уровне пропускания exp (–2).

Изготовление ПМ проводилась в два этапа. На первом этапе на пластине с хромом записывались тестовые структуры (рис. 4 а ) в виде полутонового клина (50×800 мкм), состоящего из 16 градаций серого. Затем пластина проявлялась в селективном травителе, и проводились измерения пропускания, как показано на рис. 4 б . Далее, измеряя отклонения от заданной линейной кривой (штриховая линия), эти данные использовались для коррекции мощности при записи следующей маски.

Пропускание, отн.ед. 1,0

0,8

0,6

0,4

0,2

О

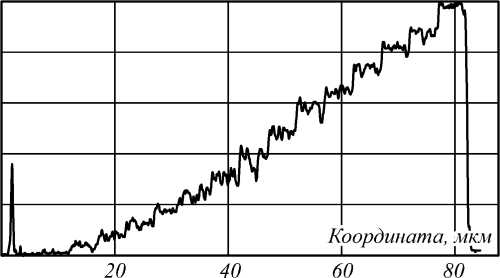
Рис. 4. Фотография расчётной полутоновой тестовой структуры (а) и график пропускания экспериментальной структуры (б)

На рис. 5 представлены результаты проверки качества изготовленной ПМ. Видно, что форма кривой пропускания полутоновой апертуры близка к расчётной. На фотографии апертуры (рис. 5 б ) видна паразитная спекл-структура, проявляющаяся в виде эффекта Муара и обусловленная влиянием как ошибок дискретизации при записи, так и частичной кристаллизацией плёнки хрома.

3.    Датчик Гартмана с аподизированными апертурами

Модифицированный датчик Гартмана состоял из описанной выше маски с Гауссовым распределением оптического пропускания по отдельным отверстиям и фотоматрицы с полем 11,264×11,264 мм и разрешением 2048×2048 пикселов (1-дюймовая CMOS GigE видеокамера Basler). Расстояние между маской и фо- томатрицей составляло 2 мм. Длина волны анализируемого волнового поля λ =532 нм.

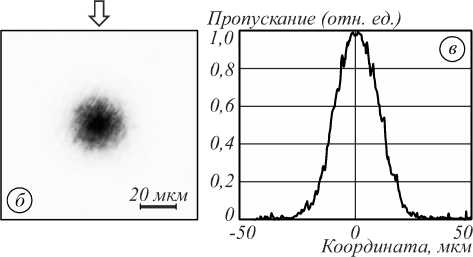
Рис. 5. Фотография фрагмента ПМ (а) (негативное изображение), увеличенное изображение одной из полутоновых апертур (б) (негативное изображение) и график пропускания в поперечном сечении (в)

На рис. 6 показан пример восстановления формы волнового фронта, полученный с использованием этого датчика. Для оценки формы волнового фронта была использована программа, в основу которой положена аппроксимация поверхности волнового фронта с разложением в ряд по полиномам Цернике с неизвестными коэффициентами [15].

Заключение

Представлено теоретическое и экспериментальное исследование гартмановского датчика волнового фронта на основе многоэлементных амплитудных масок с аподизированными апертурами. Проведён сравнительный анализ оптических характеристик амплитудных масок с резко ограниченными круглыми отверстиями и полутоновых масок (ПМ), формирующих световые пятна на фотосенсоре в виде плавных быстрозатухающих функций. Разработан и исследован метод изготовления хромовых ПМ на основе лазерного термохимического метода записи. Метод включает в себя два основных этапа: экспонирование плёнки хрома сфокусированным лазерным пучком с плавным нелинейным изменением мощности в зависимости от требуемой плотности структуры ПМ, а также проявку в селективном травителе. Экспериментально изготовлены образцы ПМ, состоящей из 64×64 Гауссовых апертур. Изготовленная маска применена в модифицированном датчике Гартмана для контроля формы волнового фронта мощных лазерных систем.

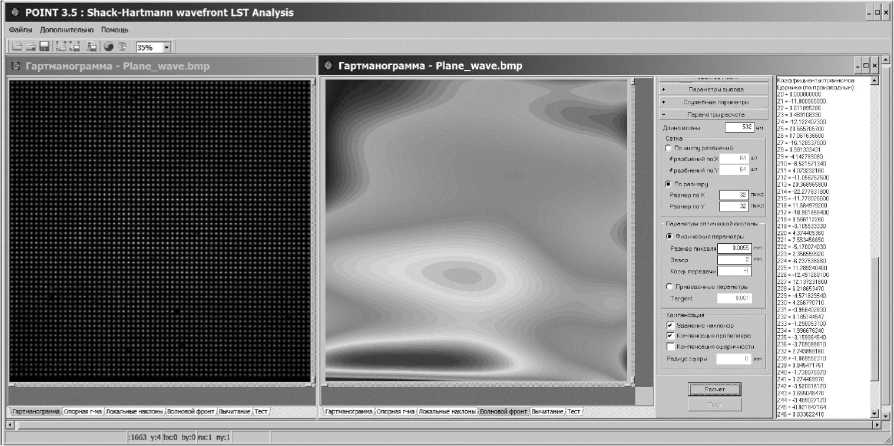
Рис. 6. Оценка по гартманограмме деформации плоского волнового фронта

Данная работа была выполнена при поддержке междисциплинарного интеграционного проекта № 112 Сибирского отделения РАН, программы фундаментальных исследований Президиума РАН, проекта 248 и проекта РФФИ 12-02-01118. Исследование по термохимической технологии записи полутоновых масок было выполнено в рамках проекта № 2012-21803-004 Министерства образования и науки РФ и проекта РФФИ № 12-02-00974-а.

Авторы благодарят коллектив лаборатории дифракционной оптики Института автоматики и электрометрии СО РАН за помощь в проведении экспериментальных работ.