Датчики ядерного магнитного резонанса как преобразователи скорости движения жидкости в частоту

В 1946 году двумя группами ученых было зарегистрировано явление ядерного магнитного резонанса (ЯМР). Это явление нашло широчайшие применения при исследовании молекулярной структуры веществ в различных отраслях науки (физики, химии, биофизики, биохимии и др.). Вслед за этим начались поиски практических приложений этого явления, что привело к ряду важных достижений: оценка продуктивности нефте-, газоносных пластов, количественный анализ мас-личности и влажности семян, магнитнорезонансная томография для медицинской диагностики, поиск воды под землей и т. д. С конца 50-х годов начались попытки применить ядерный магнитный резонанс для измерения скоростей течения жидкостей [1–3]. Применение метода ядерного магнитного резонанса для этих целей дает принципиальное преимущество перед другими методами, поскольку измерительный процесс не нарушает поток, благодаря тому что отсутствует прямой механический или электрический контакт измерителя с потоком, а измеритель не имеет никаких движущихся механических деталей. Это направление исследований привело к разработке ряда интересных лабораторных установок, в том числе в Санкт-Петербургском госуниверситете был выполнен большой цикл работ [4–8] под руководством проф. П.М. Бородина. В течение последних лет заметно возрастание интереса к научным применениям ЯМР в движущейся жидкости, главным образом вследствие увеличения роли метода в биомедицинских приложениях в качестве неинвазивного диагностического средства, в хроматографических и реологических исследованиях и др.

Целью настоящей работы является развитие систематизированных фундаментальных основ преобразования скорости движения в частоту ЯМР при перемещении жидкой среды относительно неподвижного датчика. Основные теоретические представления базируются на использовании интегральной формулы сигнала свободной прецессии, полученной на основе теоремы взаимности. Используемый авторами оригинальный подход не требует непосредственного интегрирования и освобождает от громоздких расчетов. Основные теоретические выводы настоящей работы подтверждаются экспериментальными данными. Исследования выполнялись в геомагнитном поле высокой однородности, но полученные результаты имеют фундаментальный характер, и идеи могут применяться для других ЯМР-экспериментов.

СИГНАЛ СВОБОДНОЙ ЯДЕРНОЙ ИНДУКЦИИ В ГЕОМАГНИТНОМ ПОЛЕ

Ядерный магнитный резонанс может регистрироваться в тех случаях, когда в веществе содержатся ядра с магнитным моментом. В качестве макроскопической характеристики системы взаимодействующих ядерных спинов вводится понятие вектора ядерной намагниченности M, который представляет собой суммарный магнитный момент единицы объема вещества [4].

Подобно протонным магнитометрам, в нашем случае датчик ЯМР служит для получения сигнала свободной ядерной индукции (СИ). Методика наблюдения сигнала СИ в магнитном поле Земли В 0 предполагает поляризацию ядерных спинов дополнительным магнитным полем B ( B ± B 0 , B ^* >> B 0 ), которое во время измерения выключается, с последующим возбуждением спинового ансамбля радиочастотным полем B 1 (90° импульс).

Для дальнейших рассуждений удобно ввести термин "портрет магнитных силовых линий" катушки или системы катушек. Этот портрет отражает конфигурацию магнитных силовых линий в окрестности катушки или системы катушек, через которую протекает единичный постоянный электрический ток. Согласно теореме взаимности, для оптимального наблюдения сигнала СИ портреты магнитных силовых линий катушек, обеспечивающих возбуждение и прием, должны совпадать. В общем случае поляризацию ( B ^*), возбуждение ( B 1 ) и прием можно осуществлять различными катушками, но в настоящей работе мы предполагаем, что катушка или система катушек выполняет эти три функции последовательно. Тогда распределение начальных фаз прецессий поперечной намагниченности для элементарных объемов образца, определяемое в общем случае портретом магнитных силовых линий возбуждающей к _* атуш-ки, в нашем случае характеризуется полем B^* .

Когда образец и датчик ЯМР неподвижны, в приемной катушке датчика индуцируется сигнал СИ следующего вида:

U ( t ) = U (0)sin ω ₀ t exp( - t / T ₂). (1)

Здесь ω ₀ = γ B ₀; γ — гиромагнитное отношение ядра; T 2 — время релаксации поперечной намагниченности М ; t — время.

Используемый в работе математический подход заключается в применении интегральной формулы для сигнала СИ, полученной на основе теоремы взаимности:

д с

U ( t ) =- ^∂ MK d V . (2) ∂ t_V

Здесь K = B ^*/ J^* ; J^* — электрический ток, протекающий через поляризующую катушку; V — объем образца. Векторы K и B ^* зависят только от координат, а вектор M является также функцией времени: M ( x, y, z, t ) = M f exp( i ω 0 t ) exp(- t/T 2 ), где M f = M ( x, y, z, 0) = χ B ^*( x, y, z ); χ — магнитная восприимчивость; i — мнимая единица.

Вектор M f отражает распределение начальных фаз ядерных прецессий для элементарных объемов образца, а вектор K определяется портретом магнитных силовых линий приемной катушки. В общем случае направления векторов M f и K могут не совпадать с направлением вектора B ^* и, более того, они могут не совпадать между собой. В нашем случае направления M f и K совпадают, т. к. поляризация, возбуждение и прием производятся одной и той же катушкой. Если образец и датчик неподвижны, то M f и K остаются неизменными. Движение образца и датчика приводит к эволюции векторов соответственно M f и K, что вызывает изменение параметров сигнала СИ.

Когда образец и датчик неподвижны и геомагнитное поле однородно, уравнение (2) преобразуется в уравнение (1). При преобразовании учитывались два обстоятельства. Во-первых, прецессия вектора M является более быстрым движением по сравнению с его релаксацией. Этот факт приводит лишь к появлению экспоненциального множителя в уравнении (1). Во-вторых, поскольку сигнал свободной ядерной индукции является сигналом поглощения, то нас интересует только реальная часть уравнения (2). Итак, z x dr

U ( t ) =-    MK d V =

∂ t V ∂                B ^*

=-     M _fexp( i ω ₀ t )   exp( - t / T ₂) d V =

∂ t_V               J

*2

=- ^∂ χ ^{( B} _*⁾exp( i ω 0 t )exp( - t / T 2 ) d V = ∂ t_V J

= U (0) sin ω ₀ t exp( - t / T ₂).

Здесь B ^*( x , y ) есть индукция поля поляризации и

*2

U (0) = ∫ ^{ω 0 χ (} _* ^{B )}d V .

V ^J

СПЕЦИАЛИЗИРОВАННЫЕ ДАТЧИКИ ЯМР

Датчик сигнала ЯМР в земном поле является в полном смысле этого слова определяющим элементом экспериментального устройства. Прежде всего, датчик определяет исходное отношение сигнала к шуму, которое особенно критично для слабого внешнего поля. Получение аналитических формул отношения сигнала к шуму для специальных датчиков затруднительно, обычно требуется проведение численных расчетов. Из общих теоретических представлений и формул для простых датчиков, отношение сигнала к шуму определяется индукцией поляризующего поля, коэффициентом заполнения поля катушек образцом, объемом образца, добротностью приемного контура. Помимо естественных тепловых шумов многовитко-вые катушки датчиков подвержены действию индустриальных электромагнитных помех. Для борьбы с переменными магнитными помехами используются датчики с четным числом катушек, попарно включенных встречно по магнитному потоку. Для борьбы с электрической составляющей помехи авторы используют дифференциальное усиление сигнала при отсутствии заземления датчика. Такое включение вчетверо увеличивает отношение сигнал/помеха по сравнению со случаем, когда один из входов усилителя заземлен.

Датчики ЯМР, предлагаемые в качестве преобразователей скорости в частоту, имеют одну ка- тушку (или систему катушек), с помощью которой последовательно осуществляется поляризация, возбуждение ядерного ансамбля и прием сигнала ЯМР. В эту группу преобразователей входят проточный вариант датчика тороидального типа (рис. 1, а) и датчики с внешней рабочей областью, состоящие из системы плоских рамочных катушек, обтекаемых жидкостью (рис. 1, б). В проточных и обтекаемых датчиках во время измерения неизбежно происходит вытекание намагниченной жидкости из зоны приема, что сопровождается некоторым нежелательным уменьшением интенсивности и длительности сигнала ядерной индукции. Кроме того, в проточных датчиках контролируемая область потока жидкости является труднодоступной для ввода в нее турбулизаторов. В данной работе для модельных измерений используется впервые разработанный авторами датчик типа ЯМР-кольцо с круговым движением жидкости

L 2

y

L 1

а

б

z

L 3

L 4

L 2

x

L 3

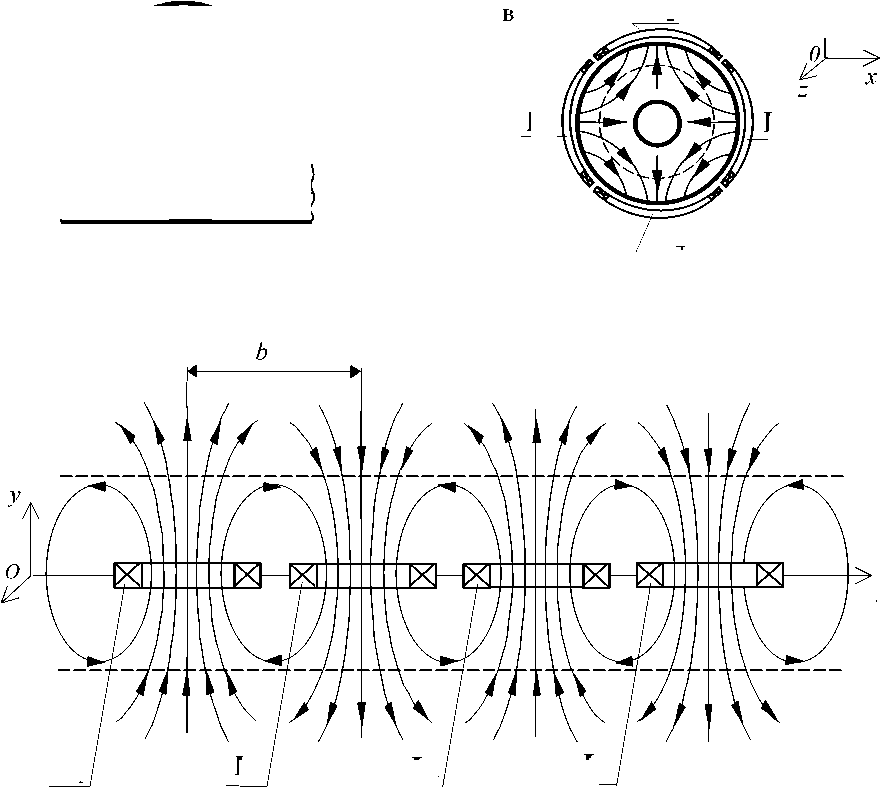
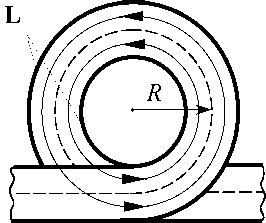
Рис. 1. Датчики ЯМР (вид сверху): тороидальный (а) и датчики, имеющие линейное (б) и круговое (в) расположение катушек.

Стрелками обозначено направление возбуждающего магнитного поля. Постоянное магнитное поле B ₀ направлено перпендикулярно к плоскости рисунка. Пунктирные линии указывают траектории движения жидкости. L — тороидальная катушка; L 1 + L ₄ — рамочные катушки; R — средний радиус тора; b — расстояние между центрами соседних катушек

L 1

L 4

в замкнутом сосуде (рис. 1, в). В этом датчике исследуемая жидкость находится в кольцевом цилиндрическом сосуде. Окружающие жидкость внешний и внутренний цилиндры могут вращаться независимо с разными частотами в любую сторону, создавая устойчивый и неустойчивый типы течений Тейлора—Куэтта. Катушки датчика рамочного типа расположены по периферии образца и служат для последовательного создания поля предварительной поляризации, возбуждающего радиочастотного поля и приема сигнала. Отсутствие вытекания жидкости не только обеспечивает максимально возможную длительность сигнала для повышения точности гидродинамических измерений, но и позволяет проводить другие физические исследования, например определение знака гиромагнитного отношения парамагнитных ядер или измерение времени поперечной релаксации в земном поле.

КИНЕМАТИЧЕСКИЙ СДВИГ ЯМР

Существование частотного сдвига следовало ожидать, поскольку этот факт был хорошо известен для тороида и ранее, т. к. впервые эффект изменения частоты ЯМР вследствие течения и создания возбуждающего поля с помощью катушки специальной формы уже наблюдался [9]. Для удобства в последующем тексте такой частотный сдвиг будет называться "кинематическим сдвигом" и обозначаться ω υ .

Рассмотрение теории кинематического сдвига целесообразно начать с ЯМР-кольца, вводя для остальных датчиков лишь необходимые изменения в полученные для ЯМР-кольца формулы.

Датчик ЯМР-кольцо состоит из 4 рамочных катушек, расположенных вокруг образца и имеющих портрет магнитных силовых линий в соответствии с рис. 1, в. Такое включение катушек создает пространственно-периодическое магнитное поляризующее поле и уменьшает влияние внешних помех. Геометри_*я катушек позволяет игнорировать зависимость B ^* от z , в то время как геомагнитное поле направлено вдоль оси 0z .

Напомним, что картина распределения начальных фаз прецессий для элементарных объемов совпадает с конфигурацией магнитных силовых линий B* и В1, а именно Mf (x, y) = χB*(x, y). Равномерное вращение образца с угловой скоростью ωвр приводит к изменению вектора Mf. Для обнаружения закономерности эволюции вектора Mf следует обратить внимание на три факта. Во-первых, благодаря спиновой памяти каждый элементарный объем образца "помнит" направление вектора Mf, которое он имел в точке расположения этого объема в момент окончания 90°-импульса. Отметим, что "запомненное направление" сохра- няется при последующем перемещении элементарного объема. Во-вторых, при вращении жидкости конструкция сосуда не позволяет изменять положение элементарных объемов относительно друг друга. В-третьих, эволюция вектора Mf имеет периодический характер, т. к. распределение начальных фаз повторяется с каждым поворотом образца. Тогда новую картину распределения можно выразить, используя первоначальное распределение:

M _f( x , y , t ) = M _f( x , y )exp( ± i ω _вр t ).

Здесь вектор M f ( x, y ) ≡ M f ( x , y , 0) описывает картину распределения начальных фаз при t = 0, а знаки "+" или "–" соответствуют противоположным направлениям вращения образца. Таким образом, вращение образца приводит к появлению дополнительной временнóй зависимости вектора М . Нетрудно продемонстрировать, что эта зависимость вызывает лишь сдвиг частоты ω вр и не изменяет другие параметры сигнала СИ.

Когда образец вращается, а датчик неподвижен, сигнал СИ преобразуется к виду:

U ( t ) =

∂

=-     M _f( x , y , t )exp( i ω ₀ t ) ×

∂ t _V

*

× ^{B (} _J ^x _* ^{, y )} exp( - t / T 2 ) d V =

=- ^∂ χ ^{( B ( x , y ))}exp( i ω ₀ t ± i ω _вр t ) ×

∂ t_V      J

× exp( - t / T ₂) d V =

= U (0) sin[( ω 0 ± ω вр ) t ]exp( - t / T 2 ).             (3)

Выбор знака "+" или "–" зависит от направлений вращения образца и ядерной прецессии.

С первого взгляда независимость времени T 2 от скорости движения жидкости в условиях неоднородного возбуждающего поля не является очевидным фактом. Конечно, когда прием сигнала СИ производится цилиндрической катушкой, дополнительные изменения амплитуды сигнала неизбежны. Если же портреты магнитных силовых линий возбуждающей и приемной катушек совпадают, то когерентность спинового ансамбля сохраняется. Это подтверждается не только вышеприведенными логическими выводами, но и экспериментальными результатами.

Рассмотрим датчик ЯМР в виде тороидальной катушки, ее портрет магнитных силовых линий приведен на рис. 1, а. Вышеприведенные выводы о поведении параметров сигнала СИ справедливы и для тороида. Обычно частотный сдвиг ωυ выра- жается через отношение скорости потока и к среднему радиусу тора R. Кроме того, эффект вытекания поляризованной жидкости из датчика игнорируется, т. к. он приводит только к уменьшению коэффициента заполнения [5]. Тогда сигнал СИ —

U ( t ) = U (0) sin[( to ₀ ± и / R ) t ] exp( - t / T ₂).

Выбор знака "+" или "-" зависит от направлений движения жидкости и ядерной прецессии.

Рассмотрим ЯМР-датчик, который состоит из 4 рамочных катушек, расположенных в одну линию (рис. 1, б). Так же как и в случае ЯМР-кольца, геометрия катушек позволяет игнорировать зависимость B от z, в то время как ось 0z направлена вдоль В0. Поле поляризации имеет пространственно-периодическую конфигурацию магнитных силовых линий, которая повторяется вдоль оси 0x через интервал 2b. Этот датчик далее будем называть "плоским датчиком". Предполагается, что все элементарные объемы жидкости двигаются по оси 0x вдоль неподвижных катушек с постоянной скоростью. Так же как и для тороида, здесь не учитывается эффект вытекания поляризованной жидкости из зоны приема. Анализ параметров сигнала СИ удобно производить, когда исследуемая жидкость разбивается на две равные части. Объем A (у > 0) — это область, расположенная по одну сторону катушек, а объем B (у < 0) — это область, расположенная по другую сторону катушек. Суммарный сигнал — d U        с

U(t) =--[MK dV + [MK dV = д t IA           B

= U A ( t ) + u , ( t ).

Рассмотрим объем А . Согласно таким же логическим рассуждениям, которые были использованы для ЯМР-кольца, можно показать, что существует временная зависимость M _f:

M _f( x , у , t ) = M _f( x , у )exp( ± nu t / b ).

Знаки "+" и "-" соответствует противоположным направлениям движения жидкости. Тогда в области A индуцируется сигнал СИ

U A ( t ) = U A (0)sin[( to ₀ ± nu / b ) t ]exp( - t / T ₂). (4)

Знак сдвига частоты зависит от направлений скорости потока и ядерной прецессии.

Нетрудно продемонстрировать, что сдвиги частот для объемов A и B имеют равные значения, но противоположные знаки. Геометрия поля поляризации позволяет написать следующее соотношение:

B * ( x , У ) V = a =- ( B * ) ⁺ ( x , У ) V = в

Здесь вектора B * и ( B * )⁺ являются комплексносопряженными векторами. Это выражение является ключевым для послед_*ующего объяснения, т. к. показывает, что поле B в объемах A и B имеет разные портреты магнитных силовых линий. Следовательно,

M f V = A =- M + V = в и K V = A = - K   = в

Тогда в объеме B индуцируется сигнал СИ

U , ( t ) =

д

=--M f( x, у, t )K (x, у )exp(i«0t )exp(-t / T2)d V = tB dr

= -- J(-Mf( x, у, t))+ (-K (x, у ))+x tA x exp(ito01) exp(-1 / T2)d V = dr....   ..

= -— (-Mf(x,у)) (-K(x,у)) exp(+ inut/b) x d tA x exp( ito 01) exp(-1 / T2)d V =

д

=--M f( x, у )K (x, у )exp(+ znut / b) x tB x exp( ito 01) exp(-1 / T2)d V =

= U_B (0)sin[( to ₀ + nu / b ) t ]exp( - 1 / T ₂).          (5)

При условии, что жидкость движется по обе стороны плоского датчика и U_A (0) = U_B (0), суммарный сигнал СИ имеет вид

U ( t ) = U (0) cos( nut / b ) sin( to ₀ 1 ) exp( - 1 / T₂ ), (6) где U (0) = U_A (0) + U_B (0). Следовательно, на огибающей сигнала СИ имеются осцилляции вида cos( nu t/b ). С первого взгляда может показаться, что одностороннее и двустороннее обтекания датчика отличаются исключительно изменением коэффициента заполнения. Однако эксперименты однозначно доказывают справедливость уравнений (4-6).

ЭКСПЕРИМЕНТ

В экспериментах в качестве исследуемой жидкости используется вода. Сигнал свободной ядер-ной индукции наблюдается на протонах в однородном геомагнитном поле. Для индукции этого магнитного поля (50 мкТ) резонансная частота имеет величину порядка 2 кГц. Описываемая далее экспериментальная методика предложена в качестве предупредительной меры против влияния вариаций геомагнитного поля на результаты экспериментов.

L 1 – L 4

z

y

B 0

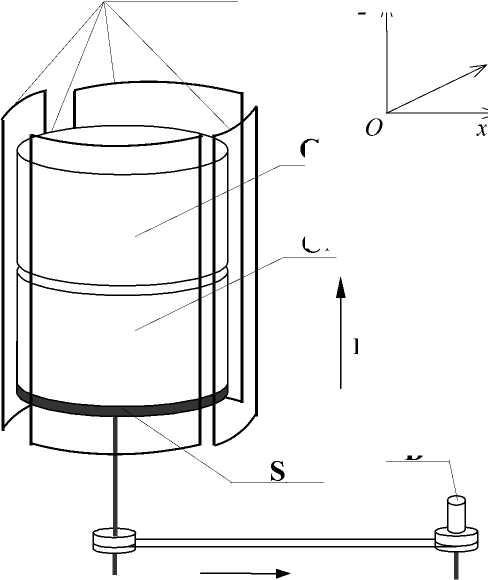
Рис. 2. Конструкция датчика "ЯМР-кольцо".

L 1 ^ L 4 — катушки датчика; C 1 — вращающаяся часть образца; C ₂ — неподвижная часть образца; B ₀ — геомагнитное поле; S — вращающийся столик; D — мотор

C 2

C 1

D

I-----------1-----------1-----------1-----------I—►

0         1          2         3         4     t , c

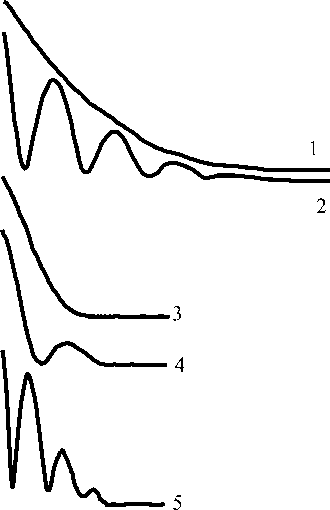
Рис. 3. Огибающая сигнала СИ, регистрируемого датчиком типа "ЯМР-кольцо", когда образец находится в двух цилиндрических сосудах. Оба сосуда неподвижны: 1 — поле однородно (градиент нулевой); 4 — поле неоднородно (градиент направлен по полю B ₀ ).

Нижний сосуд вращается, а верхний неподвижен: 2 — поле однородно (градиент нулевой); 3 — поле неоднородно (градиент направлен по полю B 0 ); 5 — поле неоднородно (градиент направлен против поля B 0 )

Два одинаковых цилиндрических сосуда с исследуемой жидкостью помещены в области, окруженной катушками ЯМР-кольца (рис. 2). Нижний цилиндр может вращаться, а верхний цилиндр неподвижен в течение всех экспериментов. Вращающийся сосуд разделяется на две равные секции диаметральной перегородкой для обеспечения вращения образца и сосуда как единого целого. Диаметр цилиндра равен 14 см, его высота равна 18 см. Максимальная частота вращения образца достигает 2 Гц ( to _вр<< to 0 ). Суммарный сигнал СИ от обоих сосудов индуцируется в приемных катушках.

Если оба цилиндра неподвижны, то сигнал СИ задается уравнением (1), и поведение его ампли- туды показано на рис. 3, кривая 1. Когда нижний сосуд вращается, то, согласно уравнению (3), суммарный сигнал СИ представляется в виде

U ( t ) = 2*^ sin( to ₀ t )exp( - t / T 2 ) +

⁺ U 2⁰) sin( ^to 0 1 ± ^to вр t ) exp( ^- 1 / T 2 ) =

= U (0) cos( to _вр t / 2) sin( to ₀ 1 ) exp( - 1 / T ₂).

Таким образом, в соответствии с теоретическими предпосылками, амплитуда сигнала должна испытывать колебания по закону cos(to врt /2) независимо от направления вращения сосуда. Полу- ченный результат хорошо коррелирует с экспериментальными данными (рис. 3, кривая 2).

Для выявления соответствия между направлением вращения цилиндра и знаком частотного сдвига необходимо создать в пределах образца градиент магнитного поля, направленный вдоль поля В0. Известно, что наличие слабого градиента вдоль оси цилиндрического неподвижного образца вызывает характерные осцилляции амплитуды сигнала СИ (рис. 3, кривая 4) [4]. Тогда СИ имеет вид sin(γGht)

U ( t ) = U (0)           sin( ω t )exp( - t / T ).

γ Ght

Здесь h — высота каждого сосуда; T 2 — время релаксации поперечной намагниченности.

Когда образец неподвижен, инверсия направления градиента не оказывает влияния на форму сигнала СИ. Точно так же как и изменение направления вращения нижнего цилиндра не оказывает влияния на форму сигнала СИ в образце, расположенном в однородном геомагнитном поле и состоящем из неподвижного и вращающегося цилиндров. Если присутствуют совместно одновременно градиент магнитного поля и вращение, то возникают амплитудные осцилляции. Их характер зависит как от величины G и ω вр , так и от направлений градиента и вращения. В этом случае суммарный сигнал СИ, учитывая ω вр << ω 0 , принимает вид

U(t)=U(0)cos[(γGh/2±ωвр/2)t]× sin(γGht) γGht

sin( ω ₀ t ) exp( - t / T ₂).

Экспериментально наблюдались сигналы СИ в широком диапазоне значений неоднородности поля и частоты вращения при разных направлениях градиента и вращения цилиндра. Наиболее наглядные примеры совместного влияния вращения и градиента представлены на рис. 3 (кривые 3 и 5). Отсутствие осцилляций на кривой 3 вызвано частичной компенсацией действий градиента и вращения. В то же время увеличение частоты осцилляций на кривой 5 по сравнению с кривой 1 связано с суммированием их действий. Анализ экспериментальных кривых, изображенных на рис. 3, полностью подтверждают вышеизложенные теоретические выводы относительно поведения параметров сигнала СИ. А именно, вращение образца в ЯМР-кольце изменяет только частоту наблюдаемого сигнала СИ и не влияет на другие его параметры. Когда направления ядерной прецессии и вращения совпадают, то частота увеличивается на величину ω вр . Если их направления противоположны, то частота СИ уменьшается на ту же величину.

Рассмотрим плоский датчик с расстоянием между центрами катушек b = 14 см (рис. 1, б). Подробно экспериментальные результаты по исследованию формы огибающей и фазы сигнала СИ для одностороннего и двустороннего обтекания жидкостью катушек такого датчика приведены в публикации [8]. Эти эксперименты показали, что для одностороннего обтекания характерны экспоненциальный спад огибающей и линейность зависимости фазы сигнала от времени, причем изменения фазы для левостороннего и правостороннего обтекания катушек имеют противоположные знаки. В случае двустороннего обтекания датчика наблюдаемые осцилляции амплитуды и резкое изменение фазы на π вызваны суперпозицией двух сигналов, имеющих фазовые зависимости, характерные для левостороннего и правостороннего вариантов обтекания. Количественно сдвиг частоты с 5 % точностью соответствовал теоретически предсказанному.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Экспериментально и теоретически показано, что движение исследуемой жидкости вдоль катушек плоского датчика, тороида и ЯМР-кольца приводит к сдвигу частоты сигнала свободной ядерной индукции (СИ). Во всех экспериментах и рассуждениях выполнялись следующие условия:

• 1)    сигнал СИ наблюдается в однородном магнитном поле B 0 ;

• 2)    элементарные объемы жидкости, не изменяя положений относительно друг друга, перемещаются вдоль катушек;

• 3)    возбуждающее поле B ₁ изменяет свое направление вдоль траектории перемещения жидкости.

В соответствии с первым условием, в неподвижном образце сигнал ЯМР наблюдается на частоте ω0 = γB0. Частота наблюдения сигнала СИ в движущейся жидкости отличается от резонансной частоты на величину ωυ. В теории волн такое изменение частоты характерно для доплеровского сдвига. В нашем случае сдвиг ωυ также связан с величиной и направлением скорости перемещения образца вдоль катушек датчика, причем мы рассматриваем вариант, когда датчик неподвижен, движется только образец. Второе условие определяет характер движения исследуемой жидкости. Согласно этому требованию, элементарные объемы жидкости перемещаются вдоль катушек плоского датчика с равными скоростями, что соответствует ламинарному потоку с плоским фронтом. В случае ЯМР-кольца элементарные объемы двигаются с равными угловыми скоростями ωвр=υ(r)/r, где υ(r) — линейная скорость элементарного объема, расположенного на расстоянии r от оси цилиндрического сосуда. Кроме того, выполнение второго условия равносильно тому, что кинематический сдвиг, обусловленный перемещением любого элементарного объема, совпадает с кинематическим сдвигом частоты сигнала, который связан с перемещением всего образца. В общем случае, если перемещение элементарных объемов характеризуется набором кинематических сдвигов, то наблюдаемая спектральная линия ЯМР может быть не только сдвинута, но и уширена по сравнению с резонансной линией в неподвижном образце.

Кинематический сдвиг пропорционален скорости для всех трех датчиков «и = ku (см. таблицу). Коэффициент к различен для разных датчиков, поскольку он зависит от конфигураций силовых линий поля возбуждения. С первого взгляда не очевидно, что можно предложить единое выражение для k, которое справедливо для всех датчиков. Единый коэффициент должен также отражать периодичность распределения начальных фаз. Предлагается, чтобы к = 2п/P. Здесь P есть период повторения картины распределения начальных фаз. Этот период численно равен наименьшему расстоянию (отличному от нуля), на которое должен быть перемещен элементарный объем, чтобы фазовая картина повторилась. При определении периода Р следует учитывать гироскопические свойства начальной фазы прецессии элементарного объема. Соотношение между периодом Р и геометрией датчика также приводится в таблице. Следовательно, аналитическое выражение для кинематического сдвига может быть записано как юи = 2пи/P [рад/с], (7) если же частоту измерять в герцах, то (7) принимает вид v„ = юи/2п = и/P [Гц].

Обращаем внимание, что этот сдвиг не зависит от сорта ядер. Необходимым условием существования кинематического сдвига является изменение

Зависимость кинематического сдвига частоты сигнала СИ от геометрии датчиков

Тип датчика Кинематический сдвиг ши Период повторения P Тороид υ / R 2nR ЯМР- кольцо to вр = u( г) / г 2пг Плоский (п / b )u 2 b направления возбуждающего поля вдоль траектории движения жидкости. Однако теоретически было показано, что поворот вектора поля необязательно должен быть пропорционален длине траектории. В частности, как это имеет место при течении жидкости через тороид. Следовательно, можно сделать важный вывод, что линейное изменение фазы сигнала, приводящее к частотному сдвигу, обусловлено равномерным перемещением жидкости вдоль катушек датчика. Это справедливо, если возбуждение спинового ансамбля и прием сигнала ЯМР осуществляются одной и той же системой катушек.

По сути, выражение (7) позволяет рассматривать вышеуказанные датчики ЯМР как первичные преобразователи скорости в частоту, а параметр к как коэффициент такого преобразования.

Если использовать датчики для измерения скорости движения жидкости, следует принять во внимание некоторые обстоятельства. Во-первых, на экспериментальные данные влияет неоднородность геомагнитного поля. Во-вторых, время поперечной ядерной релаксации СИ зависит от профиля распределения скоростей. В-третьих, диапазон измерения скорости связан с геометрическими размерами датчика.

ЗАКЛЮЧЕНИЕ

В работе изучены и систематизированы основополагающие принципы преобразования датчиками ЯМР скорости в частоту. С целью получения наглядных аналитических формул для различных конфигураций датчиков в разных условиях их применения изложение ограничено случаем монохроматического сдвига частоты ЯМР. Такой кинематический сдвиг в движущейся жидкости имеет место лишь в том случае, если элементарные объемы жидкости, перемещаясь вдоль катушек датчика, не изменяют взаимных положений относительно друг друга.

Экспериментально и теоретически показано, что линейное изменение фазы сигнала СИ, приводящее к кинематическому сдвигу частоты, обусловлено только равномерным перемещением исследуемой жидкости вдоль приемных катушек, создающих кроме того возбуждающее поле, которое обязательно изменяет свое направление вдоль траектории движения жидкости. Предложено единое выражение для кинематического сдвига сигналов СИ, которые наблюдаются с помощью тороида или датчиков с линейным и круговым расположением рамочных катушек. Этот сдвиг связан со скоростью движения образца и периодом повторения картины магнитных силовых линий приемных катушек.

Полученные результаты могут быть полезны при создании новых датчиков ЯМР различных конструкций. Однако следует учитывать, что при ламинарном течении с параболическим фронтом (и тем более в турбулентном потоке) в результате преобразования скорости датчиком появляется набор частот подобно случаю неоднородного уширения сигнала ЯМР. В этих случаях частотные сдвиги для отдельных элементарных объемов жидкости также подчиняются изложенным выше закономерностям, а интегральный эффект преобразования может быть получен теоретически с использованием численных методов. Рассмотрение этих вопросов выходит за рамки данной работы.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 05-08-50280-а).