Давление сыпучего материала в круглом силосе

Введение. Как известно, сыпучие материалы обладают как свойствами твёрдого тела, так и свойствами жидкости, что сильно осложняет теоретические исследования. Например, достаточно элементарная задача расчёта давления в сыпучем материале, находящемся в цилиндрической ёмкости, с позиций сплошного твёрдого тела [1] приводит к резкому расхождению с экспериментальными данными.

Та же задача, рассматриваемая с позиций дискретного твёрдого тела, решается в первом приближении только для частиц сферической формы, «уложенных» горизонтальными слоями с правильной геометрической «упаковкой» [2]. При этом учитываются коэффициент трения между сферическими частицами (коэффициент внутреннего трения ц,) и коэффициент трения частиц о стены ёмкости (коэффициент внешнего трения це), которые определяются экспериментально. И хотя согласие с экспериментом здесь гораздо лучше, такой подход также вызывает справедливые возражения.

Предпринята попытка решить сформулированную выше задачу, представляя сыпучий материал в виде вязкой жидкости с теми же коэффициентами внутреннего (р,) и внешнего (ре) трения. При таком подходе нет необходимости задаваться формой частиц, их упругостью, упаковкой, размерами и т. д.

Теоретический расчёт давления в круглом силосе. Рассмотрим сыпучий материал в глубоком круглом силосе (см. рис. 1).

Эле ментарный , объём

Рис. 1. Сыпучий материал в круглом силосе и цилиндрическая система координат: Н— высота силоса; R — радиус силоса; z, р — текущие координаты элементарного кольца

В силу симметрии задачи воспользуемся цилиндрической системой координат, в которой можно пренебречь зависимостью от азимутального угла, как показано на рис. 1. В слое сыпучего материала выделим элементарное кольцо, объём которого будет равным: 2 • п • р • ф • dz.

В стационарном случае сумма сил, действующих на элементарное кольцо, равна нулю. В проекции на ось О7это условие имеет вид:

ЭР                    ЭРп

0 = у- д- 2- п- р- ф • dz - 2 • п • р • ф • dz ■ —-• dz - р, • 2 • п • р • dz • —£-• dp, dz                    dp где у — плотность сыпучего материала; Pz — вертикальное, параллельное силе тяжести давление в сыпучем материале; Рр — горизонтальное, перпендикулярное силе тяжести давление в сыпучем материале.

Здесь мы, в согласии с экспериментом, полагаем, что закон Паскаля для сыпучих тел не справедлив.

В уравнении (1) первое слагаемое — сила тяжести элементарного кольца, второе — сила сопротивления движению за счёт градиента вертикального давления, третье — сила внутреннего сухого трения.

В проекции на горизонтальное направление это условие имеет вид:

cR.                    ЭР

О = 2 • п • р • dz • —2- • ф - р, • 2 • п • р • ф • —- • dz. dp '              dz

Здесь первое слагаемое — сила сопротивления сжатию (или растяжению) элементарного кольца, обусловленная градиентом горизонтального давления, второе — сила трения на горизонтальных поверхностях кольца.

Из уравнения (1), учитывая (2), получим дифференциальное уравнение для определения вертикальной компоненты давления:

О = у • д • 2 • п • р • ф • dz - 2 • п • р • dp • dz • (1 + ц²) • —- .

Проинтегрируем уравнение (3) по координате р в пределах от 0 до Р\

0 = п-у-д-/?2 - dz-п-/?2 - dz-(1+ р2)- — + С.                      (4)

Поскольку при таком интегрировании элементарный объём переходит в элементарный слой, то в последнем уравнении первое слагаемое представляет собой силу тяжести, действующую на единицу длины (вдоль радиальной оси) элементарного слоя толщиной dz, второе слагаемое — результирующую силу сопротивления (за счёт градиента давления и силы внутреннего трения), действующую на этот элементарный слой. Поскольку уравнение (4) справедливо и на поверхности р = R, то очевидно, что константа С представляет собой силу трения, действующую на боковую поверхность элементарного слоя со стороны стенки силоса и направленную против силы тяжести:

С = - р_е • Рр • 2 • п • R • dz = - р_е • к • P_z • 2 • п • R • dz

Здесь использована связь между вертикальной и горизонтальной компонентами давления через боковой коэффициент к. Рр = к -Pz (такая зависимость установлена в [3] и рекомендована в СНиП 2.02.02-85).

Общий интеграл уравнения (4) с учётом (5) можно представить в виде:

\-g-R

2-Це.к

+Q•ехр -

2-М_е 'k-Z

Если найти константу Q из условия, что на поверхности силоса давление равно нулю, то выражение для вертикального давления (без учёта зависимости от горизонтальной координаты)

примет вид

_yg-R z 1-Ve-k

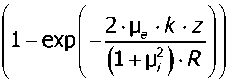
Соответственно, выражение для горизонтальной компоненты давления запишется в виде:

рР =

\-g.R

2'Ме

.            2 • р_е • к • z

• 1-ехр - Ме —

Для анализа полученного решения найдём разность Д между весом сыпучего материала в силосе и суммой сил давления на дно силоса F_D и силы трения сыпучего материала о боковую стену Ftp. Нетрудно убедиться, что эта разность будет равна:

д П-у-д-/?³

2 • ре • Ar

Из данного выражения видно, что Д = 0 в том случае, когда р, = 0. Таким образом, при выполнении условия равновесия движение сыпучего материала не происходит и внутренним трением можно пренебречь. Из (9) также следует, что если р, * 0, то сила трения в сумме с силой давления будут меньше силы тяжести, за счёт чего, собственно, и происходит уплотнение сыпучего материала в силосе.

Очевидно, что при р,^ 0, k—> 1 наступит равновесное состояние (сыпучее тело переходит в идеальную жидкость), давление по горизонтали станет равным давлению по вертикали и, соответственно, решение (7) примет вид:

^0 =

\-g.R

2'Ме

L f 2-р -z

• 1-ехр--——

R

(Ю)

Графики зависимости давлений, рассчитанных по формулам (7) и (10), приведены на рис. 2.

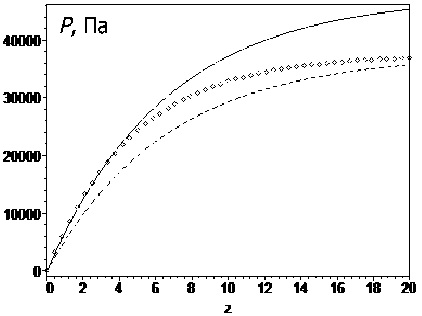
Рис. 2. Вертикальное (сплошная линия) и горизонтальное (пунктирная линия) давление в стационарном состоянии и давление (линия из точек) в равновесном состоянии для круглого силоса с сыпучим материалом (/? = 3,5 м, х = 300°, у = 800 кг/м3)

Из рисунка следует, что вертикальное давление в стационарном состоянии (сплошная линия) больше давления в равновесном состоянии (линия из точек). В то же время горизонтальное давление в стационарном состоянии меньше давления в равновесном состоянии (пунктирная линия). Следовательно, в равновесном состоянии стены силоса берут на себя большую нагрузку, в результате чего давление на дно уменьшается. Иначе говоря, в стационарном состоянии (при движении сыпучего материала) на стены силоса оказывается меньшая нагрузка, чем в равновесном состоянии, когда сыпучий материал неподвижен.

При нахождении сыпучего материала в силосе формально он не перемещается, следовательно, находится в равновесном состоянии. При этом давление в нём необходимо рассчитывать по формуле (10). Но в действительности в сыпучем материале скачкообразно происходят процессы его уплотнения, слёживания под действием микроколебаний сейсмического или техногенного характера, т. е. он находится в состоянии микродвижения. Таким образом, сыпучий материал часть времени «проводит» в стационарном состоянии, а часть — в равновесном. Соответственно, давление также меняется скачкообразно.

Введём теперь в решение (7) зависимость от координаты р. Аналогично [3] эту зависимость представим в виде:

• 1-ехр

2-р_е -k z-(/?-p)-tgxY

(И)

где х — угол естественного откоса.

Потребуем теперь, чтобы решение (11) удовлетворяло уравнению (2) с учётом того, что

Р - к . Р ■

' р 'z *

Найдя первые производные от (11) по координатам риги подставив их в равенство (12), получаем, что оно выполняется только при к • tgх = М,, т. е.

к = ^.                                (13)

tgx

Это выражение для бокового коэффициента совпадает с результатом, полученным в [3] для сыпучего материала, находящегося в насыпи.

Однако решение в форме (11) не удовлетворяет граничному условию на поверхности z=0. Поэтому для нахождения более точного решения разобьём весь объём силоса, занятый сыпучим материалом, на области (рис. 3).

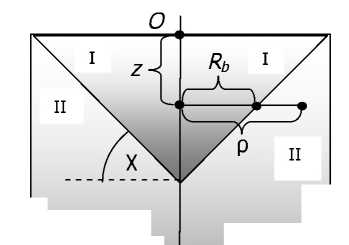
Рис. 3. Деление силоса на области: Н— высота силоса; R— радиус силоса; х — угол естественного откоса; z, р — текущие координаты элементарного кольца; Rb — произвольная точка на границе областей I и II

Поскольку в области I влияние стенок силоса ещё не будет сказываться (эта область расположена выше плоскости естественного откоса), то в этой области решение будет определяться формулой [3]:

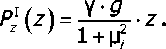
(И)

Решение в области II будем искать в виде:

^^I(p,z) = M^-fl-expf-^^-^—^ЯХ^К JL^.^-p^tgy. (15) ^v 2-м_е -k (        ( 1+p;           r           1+p; ^{v 7              v 7}

На линии z = 0 решение (15) обращается в нуль, на боковой стенке силоса (при р = /?) оно переходит в уравнение (7), а на поверхности естественного откоса (на границе областей), определяемой уравнениями p = R_b, z = (R-R_bytgx> уравнение (15) переходит в уравнение (14). Таким образом, согласование решений в областях I и II выполнено.

В случае, когда сыпучий материал находится в силосе с абсолютно гладкими стенами (це ^0), решение (15) примет вид:

lim^11 =-^^-^-(/?-р)-1дхр:^^-(Я-р)-1дх = :^

Ие^О 1 + М/                    1+М/               1+М/

Это означает, что сыпучий материал в этом случае ведёт себя как безграничная насыпь и влиянием стенок можно пренебречь, что не противоречит физическому смыслу задачи.

Итак, мы видим, что решения (14) и (15) удовлетворяют граничным условиям и предельному переходу к идеальной жидкости.

Таким образом, для идеального сыпучего материала в круглом силосе найдено вертикальное давление (15). Горизонтальное давление определяем из выражения (15) с учётом выражения (13) для бокового коэффициента.

На рис. 4 показана зависимость вертикального и горизонтального давления, рассчитанного по формулам (14) и (15), в силосе радиуса R = 3,5 м, в котором находится сыпучий материал (у = 800 кг/м³, х = 30°), непосредственно вдоль его стенки и по центру силоса. Как видно из рисунка, вертикальное давление по осевой линии силоса (р = 0) несколько выше вертикального давления у стенки силоса (р = R") и, кроме того, горизонтальное давление меньше вертикального.

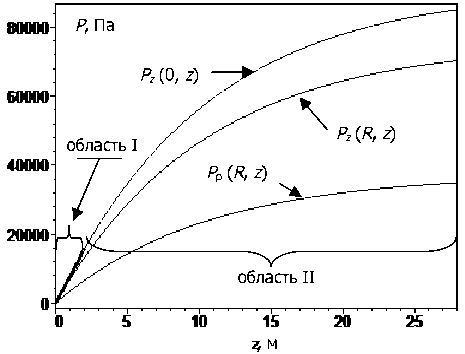
Рис. 4. Зависимость вертикального и горизонтального давления от координаты z: P_z(0, z) — вертикальное давление на оси силоса; P_z (R, z) — вертикальное давление у стенки силоса; Р_р (R, z) — горизонтальное давление у стенки силоса; радиус силоса R = 3,5 м; угол естественного откоса х = 30°; плотность сыпучего материала у = 800 кг/м³; р, = 0,287; р_е = 0,364

На рис. 5, 6 представлены графики сравнения теоретических кривых (непрерывные линии) и экспериментальных значений [4]. На рис. 5 показана зависимость горизонтального давления на стену круглого железобетонного силоса высотой Н = 21 м и радиусом R = 3,25 м, а на рис. 6 — зависимость силы давления на дно стального круглого силоса высотой Н= 6 м и радиусом R = 0,5 м.

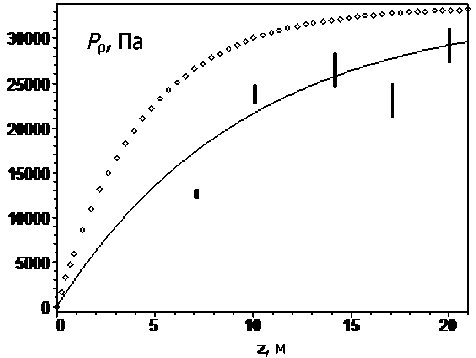
Рис. 5. Теоретическое горизонтальное стационарное (сплошная линия) и равновесное (линия из точек) давление в круглом железобетонном силосе (Н = 21 м, R = 3,25 м, х = 30°); вертикальные линии — разброс экспериментальных значений

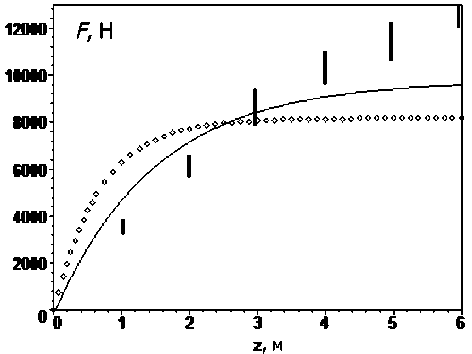
Рис. 6. Теоретическая сила давления на дно стального круглого силоса (Н = 6 м, R = 0,5 м) от высоты засыпки: сплошная линия — стационарное состояние, линия из точек — равновесное (х = 30°); вертикальные линии — разброс

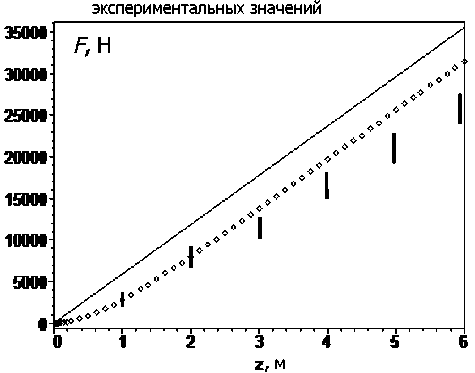
Рис. 7. Зависимость силы трения на боковую стенку круглого стального силоса (Н = 6 м, R = 0,5 м, х = 30°) от высоты засыпки: стационарное состояние — сплошная линия, равновесное — линия из точек, вертикальные линии — разброс экспериментальных значений

На рис. 7 представлена зависимость силы трения, действующей на боковую стенку стального круглого силоса высотой Н= 6 м и радиусом R = 0,5 м, от высоты засыпки.

Как видно из рисунков, разброс экспериментальных данных достаточно велик. Кроме того, само горизонтальное давление по направлениям сторон света разное [4].

Выводы. Очевидно, что этот разброс экспериментальных значений связан с процессами уплотнения сыпучего материала, со временем его выдержки в силосе, а также с тем, с какого направления идут микровибрации сейсмического или техногенного характера. Сыпучий материал в силосе всё время находится в промежуточном положении между стационарным и равновесным состояниями. Кроме того, сами параметры сыпучего материала (насыпная плотность, углы внешнего и внутреннего трения) являются некоторыми обобщёнными, мало соответствующими конкретному сыпучему материалу и, к тому же, меняющимися с течением времени. Поэтому более точного согласия с экспериментальными данными ожидать трудно.

Но из сравнения с экспериментальными данными всё же можно сделать вывод, что состояние сыпучего материала ближе к стационарному, чем к равновесному.

Таким образом, подход к сыпучему материалу как к вязкой жидкости приводит к согласию с экспериментальными данными при минимальном количестве необходимых допущений.