Давления в процессе валкового отжима кожи

DOI:

Технология обработки различных материалов с применением валковых машин широко применяется во многих отраслях промышленности. Например, парк оборудования для механической обработки кожевенного полуфабриката состоит в основном из валковых машин. Среди них можно выделит валковые машины для отжима кожи, создающие влагу, необходимую для последующих механических операций. Качество таких операций, следовательно, качество готовой продукции, зависит от эффективности процесса отжима [1].

Математическое моделирование процесса валкового отжима мокрых материалов представляет собой одну из сложнейших задач современной механики. Проблема заключается в необходимости совместного решения двух задач: первая ‒ контактное взаимодействие в двухвалковом модуле (контактная задача); вторая ‒ фильтрация влаги в деформируемой неоднородной пористой среде (гидравлическая задача). Положение усугубляется также большой величиной деформации отжимаемого материала и покрытия валков, так как в валковых отжимных машинах один или оба валка имеют покрытие из материала, имеющего вязкоупругие свойства, а также сложностью гидродинамических явлений, протекающих во времени и связанных с удалением влаги.

В процессе валкового отжима под действием давления прижимных устройств валков происходит уплотнение кожи, которое заключается в перегруппировке твердых частиц и уменьшении объема пор между ними, и сопровождается выжиманием влаги, заполняющей эти поры. Поэтому при отжиме часть приложенного давления воспринимается твердой фазой, а часть ‒ влагой. Часть давления, воспринимаемая твердой фазой, называется сжимающим давлением, а влагой ‒ гидравлическим давлением. Сжимающие давления и гидравлические давления распределяются по кривым контакта валков. Поэтому, в каждой точке кривой контакта валков, общие давления уравновешиваются сжимающим и гидравлическим давлением.

Сжимающие давления (нормального напряжения) определяют на основе изучения явления контактного взаимодействия обрабатываемого материала с рабочими валками, т.е. путем решения контактной задачи. Гидравлические давления находят на основе изучения явления фильтрации влаги в деформируемой неоднородной пористой среде, т.е. путем решения гидравлической задачи.

Анализ литературы показал, что распределения нормального напряжения и гидравлического давления, полученные в теоретических исследованиях, не соответствуют экспериментальным эпюрам, так как математические модели нормального напряжения определены без учета явления фильтрации влаги и наоборот, гидравлического давления – явления контактного взаимодействия.

Данная работа посвящена математическому моделированию распределения нормального напряжения и гидравлического давления в процессе валкового отжима кожи (кожевенного полуфабриката после красильно-жировальных операций).

МАТЕРИАЛЫ И МЕТОДЫ

Согласно [1], валковые модули кожевенных отжимных машин в основном имеют симметричный вид.

В работе рассматривается симметричный валковый модуль, в котором кожа (слой кожи) с толщиной δ взаимодействует с приводными валками, имеющими радиус R и эластичное покрытие из технического сукна с толщиной H . На рисунке 1 представлена верхняя часть валкового модуля относительно линии симметрии.

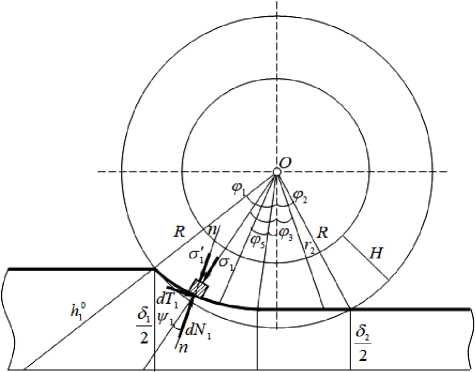
Рисунок 1. Схема валкового модуля отжима кожи.

Figure 1. Diagram of the roller module for squeezing leather.

В рассматриваемом валковом модуле кривая контакта валка (каждого) состоит из двух зон. В первой зоне кожа и сукно сжимаются. Поэтому первая зона имеет криволинейную форму. В зоне сжатия имеется сечение водораздела [2]. Жидкость слева от этого сечения движется навстречу коже, справа по ходу кожи. Поэтому в точке сечения водораздела, находящейся на кривой контакта валка, скорость фильтрации жидкости вдоль оси Ox равняется нулю. Исходя из этого, первую зону кривого контакта валка относительно сечения водораздела разделим на два участка.

В связи с тем, что кожевенный полуфабрикат в стадии отжима после красильножировальных операций имеет равномерную и тонкую толщину, она во второй зоне не будет восстанавливать деформацию, то есть не деформируется. Поэтому вторая зона (третьей участок) имеет прямолинейную форму.

В процессе отжима, вследствие действия реактивных сил, точка максимальной деформации кожи (точка, разделяющая первую и вторую зоны) будет смещена от линии центров в сторону входа кожи в зону контакта [3].

Поэтому, имеем

• -    Ф1 < 0 < -^5 , - ф < 02 < -фз , - ф3 < 0 < Ф2, или

• -    Ф1 + Фз < 01 + Фз <-ф5 + Фз, - Ф5 + Фз < 02 + Фз < 0, 0 < 03 + Фз < Ф2 + Фз, (1)

где 0,0,0 - полярные углы точек первого, второго и третьего участка, ф,ф - углы контакта (захвата и выхода), ф3 - угол, определяющий точку максимальной деформации кожи, ф5 - угол, определяющий точку водораздела, лежащую на кривой контакта валка.

Для моделирования распределения нормального напряжения и гидравлического давления в первую очередь необходимо определить аналитическую формулу, описывающую форму кривого контакта валка.

Математическую модель криволинейной зоны кривого контакта определяем с применением гипотезы о постоянстве соотношения скоростей деформации 5‘ соприкасающихся тел в зоне контакта V = Y [4] и с учетом выражения (см. рисунок 1) 5'

R ^- r i ,      .   2cosH> i + ф з ) <      cosH> i + ф з )"

• 5,    —,    5 =                 Г - R

• ¹     H        ¹          ^      ( ¹     cos( 0 + Ф ) _v

где  5*, 5 - относительные деформации кожи и сукна, у —показатель, определяющий соотношение скоростей деформации кожи и сукна при сжатии.

Тогда, имеем
2 H cos(-^ + ^ ) где m =----------------. ^	R Г 1 =-------- 1 + ту	(      cos(- ^ + ^ ) ) 1 + ту----------- (         cos( ^ 1 + ^ 3 ) v

РЕЗУЛЬТАТЫ

На первом участке кривого контакта выделим элемент длиной dl . На этот элемент со стороны кожи действует элементарная нормальная dN и касательная dT силы, которые уравновешиваются силой т ’ dl_x (рисунок 1):

Тdl_x - dN_x cos 0 o - dT_x sin 0⁰ = 0

или n1 = Т, где т’ - напряжение сжатия сукна в направлении n — n .

Согласно рисунку 1, имеем т’ = т cos ^ , или

n = т cos х//х, где т — напряжение сжатия сукна в радиальном направлении к оси.

Согласно [5, 6], кожа и сукно формализуются как сплошная среда со свойствами упругости, вязкости и пластичности и описываются реологическими моделями Кельвина – Фойгта:

d£

Т = Е £ + Цл    , Т = E 1^1. + А—, dtdt где т , £, E*, цх - напряжения, деформация, модули упругости и вязкости кожи при сжатии, т, £, Ех, цх - напряжения, деформация, модули упругости и вязкости сукна при сжатии.

Согласно формулам (2) и (5) напряжение сжатия в радиальном направлении имеет вид d^ т1 = ЕХ£Х. + ^1   -,

dt где £х

R - r_x, H

или с учетом уравнения (3)

Современные инновации, системы и технологии // Modern Innovations, Systems and Technologies 2023; 3(4)

Отсюда получим

myR Ф =-------

H (1 + my )

(

1 -

V

^{cos( -} ф 1 + Ф₃) '

COS ^ + ф ) j ’

d^

dt

myRto  cos(—ф ₁ + ф ₃)

H (1 + mу ) cos( 6 + ф )

tg ⁽6 i ⁺ ф 3 )’

где to — угловая скорость валка.

С учетом выражений (7) и (8) из формулы (6) находим

^ i

myR

H (1 + my )

E 1

V

— COS(—^1+ ф ) ( E 1 +     ^  ^3) J cos(6 + ф )                   J

Зависимость (6) и, соответственно, зависимость (9), отражают напряжения в статическом процессе. Поэтому, вместо зависимости (9) используют ее уточненный вид для динамического процесса [7]. Уточняя зависимость (9) согласно работе [7], перепишем ее в виде myR

° "₁ =-------------

H (1 + my )

⁽ E 1 + Д 1 totg ^{( —} ^ 1 + ф з )) ^{— cos(}_ ^ L± ^ l ^{) (} E 1 + ^ 1 ^totg ⁽0 1 + ^ 3 ) .

V                       cos ^ + Ф 3 )                   J

Тогда из равенства (4) находим математическую модель распределения нормальных напряжений по первому участку кривого контакта валка n1

myR

H (1 + my )

^{( E} 1 + Ц 1 totg ^{( —} Ф 1 + ф 3» ^{— COs(}_ ^ф L± ^ф 1 2

V                          cos( ^ 1 + Ф 3 )

( E 1 + Ц 1 totg(O 1 + Ф 3 ) cos ^ 1 ’

J

^{— ф} 1 ^{+ ф} 3 - ^ 1 ^{+ ф} 3 - ^{— ф} 5 ^{+ ф} 3 •                           ⁽¹¹⁾

Дифференцируя равенства (3), получим r ,== m^ cos(—ft+ ф3) tg (^ + ф )•                 (12)

+ my cos ф ( Ц + ф )

С учетом равенств (3) и (12), имеем r'        my cos(—ф + ф)

tg^ 1 = — =                   ^{1    3}          tg(6 1 + ф ₃).

Г cos( 6 + ф ) + my cos(— ф + ф )

или ф = arctgf--- mYcos( ф1 + ф3)-------tg(01 + ф3)J .             (13)

V cos( 6 + ф ₃) + my cos(— ф + ф )         J

По аналогии с формулой (11) находим математическую модель распределения нормальных напряжений по второму участку кривого контакта валка

Современные инновации, системы и технологии // Modern Innovations, Systems and Technologies 2023; 3(4) n2

myR

H (1 + my )

⁽ E i + M i totg (ф + ф з )) V

-

cos(— ф + ф ) cos( 0 + ф )

^

⁽ E 1 + ^g ( ⁰ ₂ + ф з )

cos^> ,

- ф 5 + ф з <  0 2 + ф з <  0,

где

Ф₂ = arctg

my cos(— ф + ф )

_V cos( 0 + ф ) + my cos(— ф + ф )

) tg ^{( 0} 2 ⁺ Ф з )  .

Обобщая формулы (11),  (13) и (14), получим математическую модель распределения нормальных напряжений по криволинейной зоне кривого контакта валка myR n =---------

H (1 + my )

⁽ E i + ^totg ^(—ф_х + ф з )) V

—

cos(- ф + Ф ) cos( 6 + ф )

( E_x + ^mtg(0 + Ф з) cos ^ , 7

— ф + ф з < 6 + ф з <  0,

где

Ф = arctg

my cos(— ф + ф ₃)

_V cos( 0 + ф ) + my cos(— ф + ф )

tg^{(0 +} Ф з )  ,

По аналогии с формулой (3) напишем уравнение третьего участка зоны кривого контакта валка r3

R

1 ^{+ m} i y 1 V

cos( ф + ф з ) )

1 + m 1 У1 ——--— cos(0 + ф) 7

.

При этом y_x стремится к бесконечности, поскольку для третьего участка ф = 0 .

Тогда имеем r = Rcos(ФLlФ31, 0<0 + ф <ф + ф.

cos( 6 + ф )

Формулу (18) можно получить непосредственно из рисунка 1.

По аналогии с формулой (16) находим математическую модель распределения нормальных напряжений по прямолинейной зоне кривого контакта валка

n = R ^{( E} 2 ⁺ H 2 ®tg ⁽ ф 2 ⁺ ф з )) H

^™

V

^{cos( ф 2} + ^{ф з}) ( e + ^^t,g(0 + ф ) cos( 0 + ф ), cos( 6 + ф )   ^{2    2      2 з} J          ^з

0 <  0 + ф <  ф + ф .

Положения точки приложения nmax соответствует точке максимальной деформации кожи. Тогда из зависимости (16) получим

n

max

myR

H (1 + my )

f E_x sin 2 (ф 1 —ф з

V       ^{V 2}

^

^— M 1 ^tg ⁽ф _х ^— ф з )

или после упрощения

2 HγR ( E ₁ ( ϕ ₁ - ϕ ₃ ) - 2 µ ₁ ω ) n _max =                            ( ϕ ₁ - ϕ ₃ ) .                    (20)

2( δ + 2 Hγ cos(- ϕ + ϕ ))

Аналогичную формулу можно получить с использованием зависимости (20)

_{n max =} R ( E 2 ( ϕ 2 + ϕ 3 )+2 µ 2 ω ) _{( ϕ 2 + ϕ 3).                     (21)}

Таким образом, зависимости (16) и (19) определяют математическую модель распределения нормальных напряжений по кривой контакта валка в валковом модуле отжима кожи. Для облегчения дальнейшего использования этих зависимостей аппроксимируем их более простыми эмпирическими зависимостями.

В работах [3, 8] проанализированы полученные в экспериментальных и теоретических исследованиях закономерности распределения нормальных напряжений в двухвалковых моделях технологических машин, а в работе [9] при качении колеса, и описаны различными эмпирическими зависимостями. На основе анализа графиков этих зависимостей принимаем для закономерностей распределения нормальных напряжений по кривым контакта валкового модуля отжима кожи в виде следующих эмпирических формул

n n=    max   ((ϕ1-ϕ3)2-(θ+ϕ3)2), -ϕ1+ϕ3 ≤θ+ϕ3 ≤0,           (22)

( ϕ ₁ - ϕ ₃)²

_{n =}   ⁿ max — ( ϕ 2 + ϕ 3 )²-( θ + ϕ 3 )² ,  0≤ θ + ϕ 3 ≤ ϕ 2 + ϕ 3 ,             (23)

ϕ ₂ + ϕ ₃

где n - определяется по формуле (20) (или (21)).

Сравнительный анализ графиков формул (16) и (19) с графиками эмпирических зависимостей (22) и (23) с максимальным значением, определяемым по формуле (20) (или (21)), показал, что они совпадают с достаточной для инженерных расчетов точностью.

Переходим к разработке математической модели распределения гидравлического давления по кривым контакта валкового модуля отжима кожи.

В процессе сжатия жидкость переходит из кожи в сукно вдоль полярного радиуса [2, 3].

Скорость кожи в области контакта величина постоянная и равна v .

Скорость жидкости в области отжима равна сумме двух составляющих [10]: ε ₁ v _1жx = ε ₁ v_к - u _{1 x} ,    ε ₁ v _1жy = u _{1 y} ,                               (24)

где v 1жx , u 1 x ,   v 1жy , u 1 y

-

абсолютная скорость и скорость фильтрации жидкости в зоне

сжатия вдоль осей Ox и Oy , ε - относительная деформация кожи в зоне сжатия.

В процессе фильтрации должно выполняться уравнение неразрывности [10]:

или

∂( ε ₁ v_к

-

∂ x

u _{1 x} )    ∂( u 1y )

∂ y ₁

vк

∂ε

-

∂ u    ∂ u 1y

^{1 x} + ^1y =0.

∂x   ∂x    ∂y

Переходя к дифференцированию по одной переменной θ +ϕ , запишем vк

^{ε 1′} - ^{u 1′ x} + ^{u 1′y} =0.

x ₁′      x ₁′       y ₁′

Заметим, что u1y

= - u _{1 x}ctg ( θ ₁ + ϕ ₃)

или

u ₁′ _y = - u ₁′ _xctg ( θ ₁ + ϕ ₃ ) + u _{1 x}

sin ² ( θ + ϕ )

.

Учитывая это, из равенства (25) получим

( y ₁′ sin( θ ₁ + ϕ ₃ ) + x ₁′ cos( θ ₁ + ϕ ₃ )) sin( θ ₁ + ϕ ₃ ) u ₁′ _x -       ¹       u _{1 x} = v_кε ₁′ y ₁′.

sin( θ + ϕ )

Из рисунка 1 следует, что x = r sin( θ + ϕ ), y = - r cos( θ + ϕ ) ,

Отсюда находим

x ′ = r ′sin( θ + ϕ ) + r cos( θ + ϕ ),    y ′ = - r ′cos( θ + ϕ ) + r sin( θ + ϕ ).

После подстановки производных из равенства (29) в равенство (28) и несложных преобразований находим

^r 1 ^u 1 ^′ x

-

^{( r 1′ sin( θ 1+ ϕ 3 ) + r 1 cos( θ 1+ ϕ 3 ))} u 1 ′ x = v к ε 1 ′( r 1 sin( θ 1 + ϕ 3 )- r 1 ′cos( θ 1 + ϕ 3 )).  (30)

sin( θ + ϕ )

Дифференциальное уравнение (30) является линейным. Его однородная часть

имеет решение

u _{1 x} = C ₁ r ₁ sin( θ ₁ + ϕ ₃),

откуда

u ′ = C ′ r sin( θ + ϕ ) + C ( r ′sin( θ + ϕ ) + r cos( θ + ϕ )) .

Подставив u ′ и u в уравнение (31), имеем

Современные инновации, системы и технологии // Modern Innovations, Systems and Technologies 2023; 3(4)

^C 1' = v K ^ 1' ^{( r}1 ^{sin( 9} 1 ⁺ Ф з ) ^{— r} 1 ‘ ^{cos( 9} 1 ⁺ Ф з )) .

Из равенства (2) имеем

^х =

'

^—1Г r ¹’ Ну

С учетом выражения (3), (12) и (33) из равенства (32) получим vK m cos(—Ф1 + Фз) sin2 (91 + Фз)

^С 1                                                   2

H (cos( 9 + ф ) + my cos(— ф + ф ))

или после введения допущения sin( 9 + ф ) » 9 + ф , cos( 9 + ф ) * 1

—

( 9 1 + Ф з ) 2

.

c- = _ vKm cos(—Ф1 + Фз)

1           _Ha

•

( 9 1 + Ф з ) 2 a ^{— ( 9} 1 ^{+ ф} з ^{) 2}

где a = 1 + my cos(- ф + ф ).

Интегрируем выражению (34)

c, = _ vKm cos(—Ф1 + Фз)

1           _Ha

(

—

к

a

^{( 9} 1 ⁺ Ф з ) ⁺ -yln

a + (9 + ф ) a — (9 + ф )

л

У

.

Раскладывая логарифмическую функцию в ряд и ограничиваясь членами до третьей степени относительно 9 + Ф з, имеем

С 1 =

—

v K m созе - ф . ^{+ ф} з ) 9( 9 1 + Ф з )³ + С )

3 Ha ²

или

С1 = —

v K m ^C0S( - ^{ф | + ф} 3)   , • (( 9 , + Ф з ) 3 + С ) .

3 H (1 + my cos(— ф + ф ))

Подставим это выражение в уравнение (31)

u 1 X =

—

vm ^cos( - ^ф _l ^{+ ф} з )        + Ф з )³ + С ) r ^9 + Ф з ).

3 H (1 + my cos(— ф + ф ))

Постоянную интегрирования C находим по условию, что скорость фильтрации жидкости вдоль оси Ox в точке водораздела, лежащей на кривой контакта валка, равняется нулю и_хх (— ф + ф ) = 0 :

С = (ф — ф)3.

Тогда имеем

u1 X = — b ((91 + Фз^ + ф5 — Фз )) r1 sin(91 + Фз )’

где

_{b =}     v_K m ^{cos( —} Ф 1 ⁺ Ф з )

3 H (1 + my cos(— ф + ф )) 2

Современные инновации, системы и технологии // Modern Innovations, Systems and Technologies 2023; 3(4)

Из равенства (26) с учетом равенства (36) находим

U 1 y = b (( 9 + Ф з? + ( Ф 5 - Ф з ) 3 ) Г 1 cos( 9 + Ф з ),                 (38)

При известных значениях слагаемых u и u , скорость фильтрации жидкости вдоль радиуса вектора определяется по формуле и 11 r = ^u2x + u 2 y :

^u i r = ^{b ((9} 1 ⁺ Ф з Y ^{+ (} Ф 5 ^- Ф з Y ) r i ^{cos( 9} 1 ⁺ Ф з ),

или с учетом равенства (3)

Rb C     cos(- ф + ф₃ ) Y       _{3         3}

- ^ф 1 ^{+ ф} з - ⁹ 1 ^{+ ф} з - ^{- ф} 5 ^{+ ф} з . ⁽⁴⁰⁾

^u 1 r

------- (1 + mY--------V ((91 + Фз) + (Ф5 - Фз) ), 1 + mY V        cos(9 + ф3) J

В работе [2] установлена применимость для анизотропной среды, обобщенного закона Дарси в виде dPr _“r

drk где

1 cos² 9 sin² 9

— =-----+     ,(42)

K-     K1

где pr - гидравлическое давление в направлении r ; K — коэффициент фильтрации по оси Oy , Кг - коэффициент фильтрации по оси Ox ц - коэффициент вязкости жидкости. Согласно формулам (39), (41) и (42), имеем dP 1 r = -Mb

' ^co s²( ⁹ 1 + Ф з ) ! sjn²( ⁹ 1 + Ф з ) ^Л

к

V      ^К 1

к

^К 2      J

Г 1 r /(( 9 1 + Ф з )³ + ( Ф 5 - Ф з )³) d ( 9 1 + Ф з ) .    (43)

После интегрирования выражения (43) с учетом выражений (3) и (12) и введя

допущения sin( 9 + ф ₃) * 9 + Ф з, cos( 9 + Ф ₃) * 1

—

^{( 9} 1 ⁺ Ф з )

, получим

^p 1 r

—

^ ^ ⁽ Ф 5 - Ф з ^)з( r 1 ² 2 K

+ C 2 ).

Определяя постоянную интегрирования

C по начальному условию

р , (- ф + ф ₃) = 0 и учитывая равенства (3), имеем:

MbR2

^{P 1 r} = 2 К

1 - —ц (1 + mY )

cos( - ^ + ф з ) 1 + mY ———— _v 008(9 +Ф₃) у

⁽ Ф 5 ^- Ф з ^{) з},^- Ф 1 ⁺ Ф з ^{- 9} 1 ⁺ Ф з ^{- -} Ф 5 ⁺ Ф з . (44)

По аналогии с формулой (44) запишем pbR R p2 r = 2 K

1 -

V

(1 + my )²

cos( - p + Ф )

1 + my-----------

V       cos 0 + Ф 3 ) J J

^ф 5 ^- ф аУ ,  ^- Ф 5 ⁺ Ф 3 <  ⁰ 2 ⁺ Ф 3 <  °-

По аналогии с равенством (30) для третьего участка кривого контакта, имеем r3 U ‘ x

—

( r‘ sin( 0 ₃ + ф₃ ) + r cos( 0 + ф₃ )) , --------—----:--------^u ‘ x

sin( 0 + ф ₃ )

= v_K ^‘ ( r sin( 0 ₃ + ф ₃ ) - r‘ cos( 0 + ф ₃ )).

Из равенства (18) находим r.= R C«M + p,)     + ^

3           33

cos ( 0 + ф ₃)

С учетом выражения (18) и (47) по аналогии с равенством (30) получим

^U 3 x

—

sin( 0 + ф ₃) cos( 0 + ф ₃)

и 3 x = о .

Это уравнение имеет решение

^U 3 x = ^C 3 tg ^{( 0} 3 ⁺ ф а ) .

Когда 02 + ф3 = 03 + ф3 = 0, то имеют место равенства u2х(0) = u3х(0) = 0. Отсюда имеем, что С3 = 0. Тогда из равенства (31) и по аналогии с равенством (4) следует, что м3 = - 0 и и3у = 0, соответственно

Ur = 0,  Pr = 0, 0<03 + ф3 <Ф2 + ф3.(49)

Обобщая формулы (44), (45) и (48), имеем

^bR   !       1      1      cos(-p + ф3 )    zА

Pr =^~ ^{1 -}7_Л -----77 ^{1 +} mY ---------- ⁽ ф 5 ^- ф 3 ) , ^- ф 1 ⁺ ф 3 < ^{0 +} ф 3 <⁰,

2 K ^   (1 + mY )² V        cos( 0 + ф ) )

Pr = 0,   0 < 03 + ф3 < ф2 + ф3-(50)

Зависимость (50) определяет математическую модель гидравлического давления по кривым контакта валкового модуля отжима кожи.

Таким образом, получены математические модели закономерностей распределения нормального напряжения и гидравлического давления при валковом отжиме кожи (кожевенного полуфабриката после красильно-жировальных операций).

Анализ графиков полученных математических моделей показал, что они соответствуют экспериментальным эпюрам, полученным при отжиме различных материалов.

ЗАКЛЮЧЕНИЕ

• 1.    На основе решения контактных и гидравлических задач валкового отжима кожи получены математические модели закономерностей распределения нормального напряжения и гидравлического давления при валковом отжиме кожи (кожевенного полуфабриката после красильно-жировальных операций).

• 2.    Полученные математические модели распределения нормальных напряжений аппроксимированы более упрошенными эмпирическими зависимостями с максимальным значением, определяемым по разработанным моделям. Сравнительный анализ графиков полученных математических моделей с графиками эмпирических зависимостей показал, что они совпадают с достаточной для инженерных расчетов точностью.

• 3.    Выявлено, что нормальные напряжения изменяются от нуля в начале и в конце зоны контакта валков до максимума в точке максимальной деформации кожи, а гидравлические давления изменяются от нуля в начале зоны контакта валков до максимума в точке максимальной деформации кожи, после этого и до конца зоны контакта валков это давление равняется нулю.