Day-ahead Pricing Model for Smart Cloud using Time Dependent Pricing

Published Online October 2015 in MECS

Cloud computing is a large scale parallel and distributed computing architecture in which virtualized machines, multi-tenancy, computing power, memory (storage), infrastructure for computing, software and platforms are delivered on demand to external customers in a business oriented environment [1]. Cloud service providers charge their consumers with ‘Pay-as-you-go’ model in which the consumers have to pay for the services they use [2]. Consumers should have a guarantee that the services they are paying for should be delivered to them uninterrupted. This is provided through SLAs (Service Level Agreements) between the consumers and providers. There are several challenges in cloud computing pricing schemes and an efficient economic model is the emerging challenge for an enterprise working in the field of cloud computing [3].

Cloud computing can trace its roots from grid computing and cluster computing. These all can be promising paradigms to provide IT as a service to end users. The service providers have not only to provide these attributes or capabilities to the consumers, they also have to do it efficiently because this will be a business of more than a trillion dollars in the coming years. There are several problems which providers as well as consumers bear in the usage of cloud computing as a utility service. Several pricing techniques have been used by big giants in the field of cloud computing.

“Pay-as-you-go” is a model which is used by several SaaS providers to provide services to their consumers. This model works on the principle of ‘the more you consume, the more you have to pay’. This model features cloud computing as utility computing. Several cloud computing providers use this approach as a pricing technique which includes big giants of the IT industry like Google App Engine, Amazon and Microsoft Windows Azure [4] [5] [6]. This model makes cloud computing environment very flexible, because the cost is calculated on the basis of usage. vThunder Pay-As-You-Go Licensing Model provides various IaaS providers to offer servers L4 and L7 advance networking tenant details and services like reporting, billing, license management and metering [7]. The service it provides makes it elastic and flexible for various Cloud Service Providers (CSP). Consumers can adopt vThunder with automated licensing possibilities which are Rental Billing Model (RBM), Utility Billing Model (UBM). The working of RBM and UBM is shown in Table 1.

Table 1. Difference between Different Pay-As-You-Go Business Models

RBM (Rental Billing Model)	UBM (Utility Billing Model)
This model generates bills with a fixed bandwidth, license for a given period of time say a month.	This model generates bills based on consumption, license per byte.
Bandwidth is fixed with some MBPS increments.	Billing is based on actual data consumed.
Deterministic   approach   for billing.	Non Deterministic approach for billing.

The basic motivation of smart cloud computing is to constitute a framework which is automated and can distribute cloud resources over a communication network that uses two-way communication between service providers and consumers. In this model a Cloud

Workload Management System (CWMS) is used which act as an interface between the consumer and the service provider which manages the customer’s resource requirements, and clusters the cloud resources using the k-mean clustering algorithm. This leads to more support for demand response of resources using an economic model called the Time Dependent Pricing (TDP) model. Smart cloud computing environment works on calculating prices of cloud resources using TDP. The cloud resource providers are required to send resource pricing information from their records (database) to Compromised Cost-Time Based (CCTB) scheduling policy located at the CWMS interface. CCTB can observe and manage a consumers’ resource requirement and scheduled it at peak and off-peak periods. Resources can be scheduled automatically or manually by CCTB depending upon the pricing at various hours of the day. Such approach helps resource providers to practice a versatile pricing to increase their profits/revenues by covering off-peak demand and executing a better cloud resource consumption.

The rest of this paper is organized as follows: Section II introduces our motivation behind building this pricing algorithm. It states some pervious related works and their contribution to the economic aspect of cloud computing. Section III introduces our pricing algorithm and consumer behavior model. We propose a model of calculating the ideal day-ahead pricing using shifting workload function defined in Section IV. Section V shows the results of the pricing algorithm approach. And lastly, Section VI infers the paper by briefing the outcomes and discusses future aspect and further research.

• II.    Background and Related Work

Several earlier works have been done in the cloud computing pricing schemes, some of these works focus on resource providers (i.e., minimizing cost and increasing revenue) and some are consumer oriented (i.e. increase in QoS to its consumers). A Novel Financial Economic Model is Cloud Compute Commodity (C3) pricing model. Buyya et al. proposed a pricing model which they designed, simulated and developed with two constraints in mind, which were providing dynamic flexibility in terms of QoS to its users and profitability for its resource providers [8]. Various cloud resources provided by the vendors or providers are called C3 (Cloud Compute Commodity). Dhawas et al. focused on the security breach and outrage of user’s data on the provider’s side [9]. This secure model focuses on how a data copy is to be maintained over other providers, in case any one of the providers goes unavailable or bankrupt. The proposed model uses the linear programming technique to suggest the given secured cost model. They have developed an economical destitution of user’s data over several providers with availability of data where secure storage takes place for several providers. Sururah et al. proposed ideas about how flexibility in the pricing model associated with cloud computing can be achieved for SaaS users [10]. They implemented different use-cases to understand the possible pricing schemes for its consumers in the cloud computing environment. The rewards given to the user on the basis of its usage of cloud are also discussed. In this pricing scheme the main attention is on TDP to maximize the profit and minimize the cost of a cloud service provider. The cloud resource provider's approach to discover prices, according to consumers’ response have been considered in various previous works: some researchers proposed pricing techniques on the basis of an auctioning model, in which an auctioneer has the ability to set the pricing strategy which both provider and its consumers accept. Like Shifeng et al. study the recent flaws in the cloud market and proposed a Double Auction Bayesian-Game based Pricing Model (DABGPM) [11]. Through this approach, they first developed a cloud market, which is uniform and competitive to several cloud service providers. It focused on how a pricing scheme could be more flexible in resource trading. Whereas Kento et al. proposed a mechanism by which users can enable the current services in spot market and future services in the forward market [12]. Users can also demand a mixture of coallocations and services of the resources together. The authors of this paper suggested and simulated a model considering the future aspects of cloud computing where thousands of customers bid for a suitable resource. The pricing algorithm proposed by Pourebrahimi et al. is based on a traditional pricing economic model [13]. The authors simulated their pricing algorithm on a continuous double auction mechanism. They simulated the results on the grid environment considering three aspects: balanced network, task intensive network and resource intensive network. The dynamic pricing approach proposed in Michael et al. calculates the prices of the resources in a combinatorial grid [14]. It provides two types of pricing techniques in a combinatorial grid. The scheduler is responsible for allocation of resources. The types of pricing techniques used are Shadow Pricing and Scarcity Pricing. The pricing technique uses an auction type economic model called English Auction. The Shadow pricing is based on the linear distribution of resources, whereas the Scarcity pricing overcomes the problem of the linear pricing program. The pricing scheme proposed in are all examples of auction based pricing strategy [1114]. The Table 2 summarizes the function of these pricing techniques which are discussed above.

Our contribution to the aforementioned works is proposed in this paper. This work is an extension of our previous work [15]. We have extended the CCTB scheduling technique [15] to a TDP scheme focusing on the heterogeneity (i.e. every consumer has different priorities of cost and time) at the consumer level.

• III.    Model Formulation

In this paper we present a pricing model, this model emphasizes on the day-ahead time-dependent pricing for cloud computing, which is dynamic in nature [16]. Previous works give high uncertainty to its consumers. Many customers favor a day-ahead compromised cost- time based versatile pricing scheme. Its main advantage is that it allows its consumers’ to plan their schedule of resources in advance. The framework of proposed model is shown in Fig.1.

Table 2. Summary of Related Work

Pricing Model	Economic Model	Provider Perspective	Consumer Perspective	Justice
Buyya [8]	Commodity Market Model	V	V	It helps providers to recover its investment before the age of resources
Dhawas [9]	Posted Price Model	X	V	The main focus of this model is to overcome the security issues
Sururah [10]	Commodity Market Model	X	V	This model is consumer oriented as they provide rewards to its consumer
Shifeng [11]	Double Side Auction Model	X	V	More centric towards consumers but helpful for providers as well.
Kento [12]	Double Side Auction Model using K pricing	X	V	Consumer specific, can order its requirement from spot/forward market
Pourebrahimi [13]	Double Auction Approach with continuous aspect	V	X	Beneficial for the providers due to decision making approach.
Michael [14]	Double Auction Approach(English Auction)	X	V	It is beneficial for the user because they purposed a scarcity pricing approach

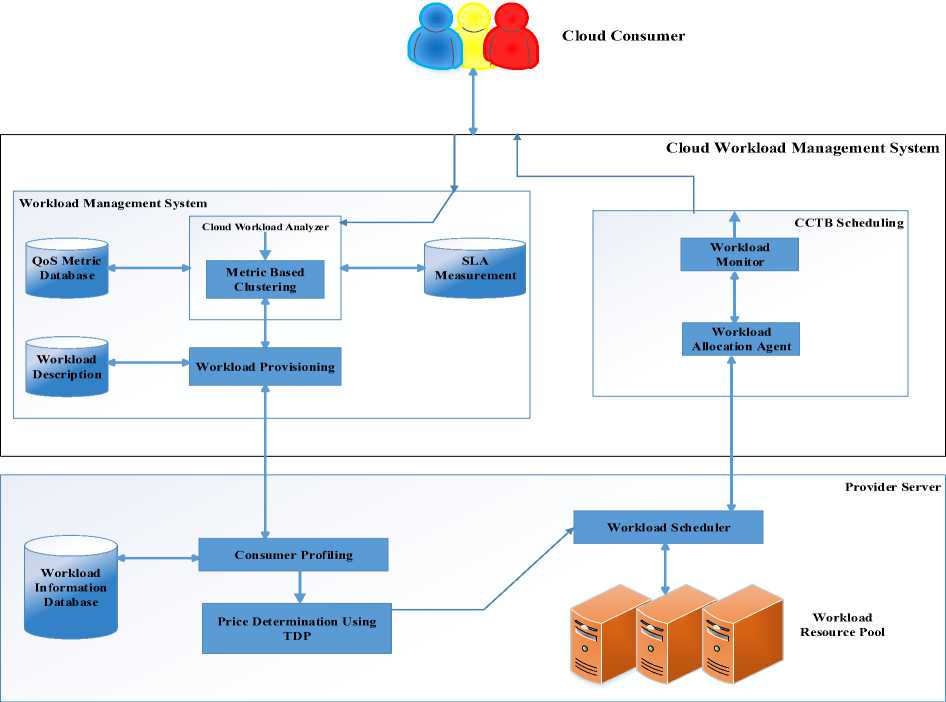
Fig.1. Cloud Workload Management System using Time Dependent Pricing and CCTB Scheduling

Also, this approach of pricing technique uses CCTB for scheduling, which provides Quality of Service (QoS) constraints to achieve better utilization of computing resources. With this feature, this model can prove to be docile and scalable to a large number of consumers. The behavior of consumers can be calculated on the basis of earlier observations. Our approach indicates that using this model for cloud computing pricing strategy can help the providers to increase their revenues and minimize the execution cost and the execution time. Finally, this research has been simulated and tested on CloudSim [21]. The final result of the system is to optimize the service provider’s cost minimization problem and use a day-ahead pricing model.

The following points outline our model:

• •    This model uses a dynamic pricing approach that can maximize the provider’s revenue and minimize the execution time and cost of resources.

• •    A cloud workload management system (CWMS) is a combination of WMS and CCTB. WMS (Workload Management System) analyzes the requirement of the consumers’ workload, clusters that workload through K-means clustering algorithm and assigns weights to each cloud resource [15].

• •    This model works with TDP to function exactly like the flat-rate pricing model. The rewards/discounts awards provided will be based on previous usage. So, the prices of cloud resources will follow TDP at any given instant of time.

• •    The CCTB can schedule consumers’ resources according to the negotiated cost and execution time because the prices are known to providers a day ahead. Most techniques do not heed to day-ahead pricing and also do not use TDP as a baseline for the economic model.

In this schematic architecture, TDP which is a versatile economic model acts as a feedback loop between providers and consumers as shown in Fig. 2. The resource provider observes the cloud workload to evaluate the amount of demand that can be shifted, the consumers’ response to these prices, is scheduled by CCTB, by which the provider can refine its estimate and maximize its revenue.

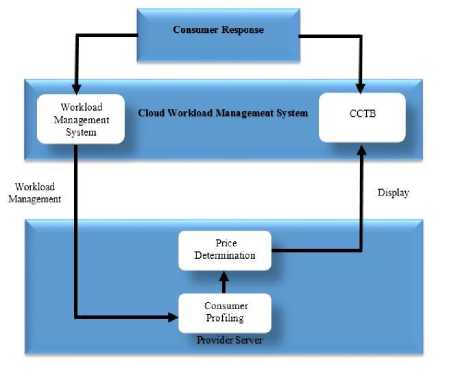
Fig.2. Schematic Behavior of Feedback Loop between the Resource Provider and Cloud Consumer

Suppose, we divide a day into n periods, e.g. n = 24 to represent cloud resource’s hourly price of a day. The provider will receive the demands for the resources in each period, say W i where i represents the index of n periods. The demand for an existing consumer is roughly same for a particular time of the day due to cyclic replicated cloud workload consumption (e.g. hour 10 in Fig. 3 has the same consumption on weekdays).

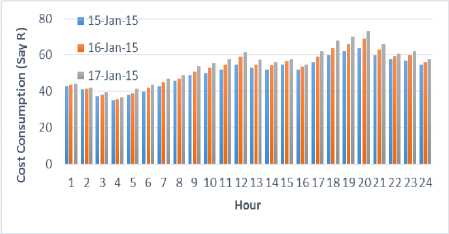
Fig.3. Hourly Cost Consumption for Workload Remains Same For Three Consecutive Days

Therefore, cumulative demand for each period is taken to be roughly constant for 3 consecutive days. It remains almost similar from hour to hour. R i is the average cost consumed and charged by providers to consumers for a given i period. The above depicted study further highlighted that there has been a demand of cyclic nature of workloads over an hour of the day and similar nature of demand (cumulative) is also reflected.

Here we are assuming that there is no loss in the total workload using TDP, it means that a user will have the same amount of workload as he had before the introduction of the TDP model. By the ease of TDP, the workload is shifted from one period to another and the workload is not lost. This is also valid whenever the scheduling through CCTB is done, thereby the workload is automatically made to schedule over a period on the basis of a compromised cost and time based scheduling [15]. The proposed approach in this paper is a feedback loop between its consumers and providers. The architecture follows a systematic approach as shown in Fig. 2. The model is based on three key steps as explained subsequently.

First, consumers interact with workload management system (WMS) in the environment of CWMS. The main task of workload management system is that the cloud service provider provides the workloads associated with its smart cloud computing environment to its requested consumer on the Cloud Workload Management Portal. CWMS uses the K-means algorithm for clustering the various workloads specified in the Table 3. Each workload has its own demand on the basis of QoS requirements. This demand of various workloads cannot be assigned on the basis of a simple static provisioning model. Hence a k-means clustering algorithm which is proposed in [15]. Clustering algorithm is used to cluster the associated workload for this day-ahead pricing model. “k-means” is a non-hierarchical algorithm and in its initial step creates a number of clusters equivalent to the number of population of workloads. The CWMS provides consumers an interface through which they can select the resources they need (specified in the Table 3). Then it assigns weights on the basis of QoS associated with that workload on a scale from 1 to 5.

The various types of workloads which are recognized by this paper are hosting websites, technological cloud computing, endeavor software, computing performance testing, online transaction oriented application, ecommerce, online financial services, backup and storage services, production application for cloud, project development and testing, graphics project, critical applications and mobile services [17]. Table 3 summarizes these cloud workloads. This table also gives a unique identification to each workload. Various cloud workloads which a consumer can demand from the provider are categorized on the basis various QoS metrics. Metrics can be security related, bandwidth need, computing capacity etc. Time dependent pricing is applied on the listed workloads in Table 3. These workloads listed in three categories on the basis QoS requirement. The three categories are Server oriented workloads, Client oriented workloads and Mobile oriented workloads.

Table 3. Cloud Workload Categorization in WMS [15]

Workload Category	Cloud Workloads in CWMS	QoS Parameters-Weights
Server Oriented Workload	Hosting websites (W1)	Storage efficiency-3 Network bandwidth-3 Availability-5
	Technological cloud computing (W2)	Capacity of computing-5
	Endeavor software (W3)	Security- 5 Availability-5 Confidence level of customer-3 Correctness-3
	Computing performance testing (W4)	Capacity of computing-5
	online transaction oriented application (W5)	Security- 5 Availability-3 Accessibility of internet-5 Usability-3
	e-commerce (W6)	Load of computing-5 Customizability-3
	Online financial services (W7)	Security- 5 Availability-3 Changeability-1 Integrity-5
	Backup and storage services (W8)	Reliability- 5 Persistence-3
Client Oriented Workload	Production application for cloud (W9)	Network bandwidth-2 Latency-3 Backup of data-4 Security-5
	Project development and testing (W10)	Self-service rate-4 Flexibility-4 Infrastructure service-1 Testing time-5
	Graphics project (W11)	Network bandwidth-3 Latency-3 Visibility-4
	Critical applications (W12)	Availability-5 Usability-3 Serviceability-4
Mobile Oriented Workload	Mobile services (W13)	High Availability-3 Reliability-5 Portability-2

The weights associated to each cloud workload are shown in Table 3. Singh et al. enhance these thirteen workloads associated with one or more QoS requirements from the listed twenty-four [15]. The weights associated with each workload QoS parameter is based on an average value assigned to that parameter in different research papers. WMS manages these workload resources efficiently using k-means clustering algorithm. And the distance is calculated using the four values of seeds and by using the k-median method [18]. The result is taken from the tables given in [15]. The clusters formation is calculated using two iterations and these thirteen workloads are classified into four seed clusters. After two iterations the number of workloads remains same in each cluster. Singh et al. provide an efficient way of clustering the given workload and carefully observed that number of workload in a cluster remain almost same.

Second, after clustering, we use a variable R to denote usage price that a cloud service provider charges from its consumers without TDP. We can use TDP in the terms of discount/reward to the usage price R. Discount ( r_i ) for every hour i, i= 1, 2, … ,n where n=24. The day-ahead pricing technique assists consumers to shift their workloads to earlier or later period from the “actual period” of computing to get maximum rewards. The maximum reward across all n period is taken as R, because resource providers never charge negative prices from their customers.

There has been a trend of paradigm transition from the periods originally calculated by shifting workload function p j (r,t), which calculates the probability of shifting each consumer usage to a given time t, whereas r denotes the discount/reward in shifted period. The shifting workload function may vary from consumer to consumer. The subscript to shifting function j denotes consumer device parameterization. This function assumes to increase in discount (in terms of shifting the load with the law of diminishing marginal utility) and there has been a decrement in the time period (i.e. there is preference for shifting workloads to off-peak periods by the consumer). As shifting functions are probabilistic, it can normalize every shifting function over the entire days’ time t if p j (R, t) . Shifting of workload never exceeds the actual consumption ensured by normalization.

This paper assumes the each hour of a day is one unit of time and the representation of each hour period is done by i, where i equals to 1,2,3,4…,n. if a transition in consumption of the consumer occurs from hour i to hour k; where k can be greater than i or less than i. The total amount they shift is given by k – i hours, where k – i lies between [1, n ] e q . It is equivalent to k - i = q (mod n ). There is congruency between q and k – i modulo n. Consumers transfer their workload to next day’s hour k if i >  k . With this the consumers get the opportunity to shift their workload to k hours before or after hour i . There are some workloads which are never turned off. In this algorithm, it assumes a demand of baseline w_i in every hour i . This is the amount of workload which can never be shifted. With this an optimized problem of cloud computing service provider can been formulated.

Next, we formulate an expression of cost of discount/reward offered and later we will express the formulation for consumer satisfying cost. Discounts/rewards are given by r1 ,r2,........rn in each hour over a day. First, we need to calculate shifted demand of workload from each hour i into each hour k. We calculate the amount of workload needed by each consumer in the hour i, then multiply it by shifting probability. The overall sum for each user is given by

^∑ j ∈ W_tPj ( r_k , ^| к ^- i |) Uj ,                  (1)

W_i which includes all group of consumers workloads initially (i.e. without having Time Dependent Pricing) in hour i . uj is the total workload demanded by consumers’ device j (this refers to heterogeneity at the consumer end, a consumer can have more than one interface and can use more than one workload simultaneously). The total shifting of workload into an hour i is given by

^∑ k^i ^∑ j ∈ W_kPj ( П , ^| к ^- i |) Uj .             (2)

The sum of all cost (discounted/rewarded) offered is given below

^∑ 1=1 ^ri ^∑ k^t ^∑ j ∈ w_kPj ( n , ^| к ^- i |) Uj + Tidi (3)

In this section the expression we are going to introduce a method to calculating the cost of satisfying consumer demand. Cloud service providers can categories their servers into two categories: base-load servers and on-demand servers. The based-load servers have a low operating cost as compared to on-demand servers. Baseload servers have a higher capital cost than operational cost and these servers run continuously to serve the cloud consumers need, whereas on-demand servers have a higher operational cost as compare to base-load servers. In any given hour, if a consumer needs a workload and base-load server is not able to fulfill the demand of consumers, then an on-demand server must fulfill the needs of the consumer.

Linear type of behavior for different operational cost (slopes) has been modeled in this algorithm for the cost of load servers. Usage charges and operational costs are taken into consideration for calculating these incremental costs. Operational cost is assumed to be uniform throughout the study while the usage cost is made to vary throughout. ci1 denotes the incremental cost of using an on-demand server without having base-load in hour i . The random variables are a type of incremental cost; to optimize the provider’s cost problem, random variables values can be solve exogenously. The linearity of cost structure of both servers’ on-demand and base-load servers) is shown in Fig. 4; c_i0 shows the slope of baseload server workload handling cost.

Incremental cost and base-load workload handling capacity can vary from hour to hour. So Ci0 and Ci1 show the workload handling capacities in respective base-load and on-demand servers in hour i. The capacities here we took are the samples of random variables taken from price independent (i.e. exogenous) distribution. We can apply these instances, time-series algorithms like tripleexponential to calculate the capacities of base-load and on demand servers on the basis of historical data. This prediction can help to calculate the provider’s cost minimization if consumers demand exceeding the on-demand and base-load servers.

The demand in each hour i is given below, using (1)

W_t -∑ k^i ^∑ i ∈ W_t Pj ( r_k , ^| к ^- i |) Uj +

^∑ k^t ^∑ j ∈ W_kPj ( П , ^| к ^- i |) Uj .           (4)

The cost of satisfying consumers’ workload demand in respectively hour i is given by (5)

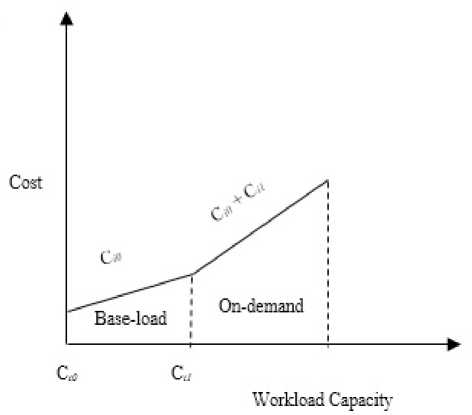
Fig.4. Linear Cost Structure of On-Demand and Base-Load Servers

]      (5)

∑       [ Wt -∑ кФ1 ^∑ j ∈ w_tPj ( r_k , ^| к ^- i |) Uj ⁺

^∑       [_∑ k^i ^∑ j ∈ W_kPj ( П , ^| к ^- i |) Uj ^- Ctz

Where [ x ]⁺ shows the maximum of 0 and x. Combining (3) and (5) and expression for providers cost minimization.

_∑ 1=1 ^ri ^∑ k^l ^∑ j ∈ W_k Pj ( n , ^| к ^- i |) Uj + tidi +∑Z=1 C[_z

[ Wt -∑ k^l (∑ j ∈ Wt Pj ( r_k , ^| к ^- i |) Uj +

∑i∈WkPj(П,|к-i|)Uj)- Ctz](6)

s.t. rt≥0,i=1,2,3,…,n(7)

var. rt ,i=1,2,3,…,n(8)

The equations (6-8) explain the service provider’s optimization problem with large number of consumers and hours. As the shifting workload function and capacity vary frequently, the prices of service provider’s cost minimization also vary. So, we need a dynamic pricing algorithm that adapts to these changes.

The algorithm which uses provider’s cost optimization problem is given below:

Algorithm 1. Calculating Day-Ahead Pricing- TDP

• 1.    Clustered every workload using k-means algorithm.

• 2.    Calculate the capacity of servers for next n hours.

• 3.    Solve (6-8), using the capacities computed in the earlier step to get optimal discount/reward.

• 4.    while the cloud resource providers’ implements TDP do

• 5.    Evaluate for the upcoming n hours the capacities of servers.

• 6.    Calculate steps (6-8) for estimating the discount for n hours in advance with the help of servers’ workload predicted and earlier calculated rewards/discount for the following n -1 hours.

• 7.    if it is hour n then

• 8.    Compute shifting workload function method in section IV.

• 9.    end if

• 10.    end while

By the help of this model, the different service provider sets up the time-dependent pricing by predicting every hour’s capacity over the next day’s hour and prices. In the initial stage, the provider sets the TDP (timedependent pricing) for hour 1 of the first day. The discount (reward and prices) on each day for each hour 1 to n , is computed prior to the first hour. On the first day, at the end of hour 1, the provider calculates the capacities of hour one on the next day. Calculations of the discount of hour 1 for day 2 are done by enhancing the expected cost from hour 2 of day one to hour 2 of day 2. These calculations are done for as long as TDP runs for calculating the day-ahead discount.

In the final third step, all the workloads are scheduled for its consumer using CCTB [15]. Information regarding the workloads and its computational resources is sent to a workload allocation agent. Cloud workload management framework calculates the deadline time of its workload. The QoS factor is also represented in scheduling of each workload. The fundamental success behind using CCTB scheduling policy is that it mainly focus to minimize the execution time as well as cost.

• IV.    Shifting Workload Function Estimation

As used in section II, for applying this pricing algorithm, the provider needs to calculate consumers’ shifting workload functions. This section uses a method to calculate the same with a function using best-fit curves. We use only aggregate data for calculating this function; it doesn’t track every individual usage in real time.

For calculation of shifting workload function, we use a function in which consumers discount/reward amount increases but time decreases exponentially as:

p_Y ^(r, 0 = с_у (_{t +1}) _У,                   (9)

where Су is a normalization factor constant. We use у as tolerance index, it calculates consumers’ willingness to shift its workload usage to after or before its original operational hour. у is a changeable parameter, higher value у indicates more intolerant consumer, the consumer which is less prepared to move his workload for extended hours of the day. Fig. 5 gives a clear understanding of different values of у with an average period of shifting workload in a flat-rate pricing model in the absence of TDP. In this algorithm the main focus that shifting workload function is simply a mathematical expression to its consumer performance, so this can be well calculated with functions like (9).

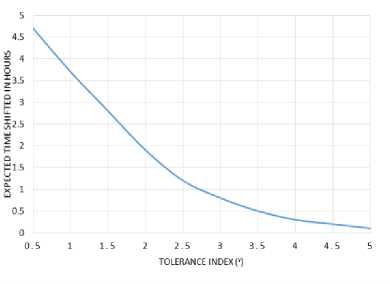
Fig.5. Average Shifting Hours over Several Different Values у under a Flat Rate Pricing.

This estimation algorithm is used to predict the individual у values for various different consumers. For simplicity, we include all values of у for a given hour into single collective shifting workload function, by adding the all shifting workload functions for each instance in the given hour, subjected to workload consumption by each instance (device), in hour I, the collective shifting workload function is:

Pi ⁽r, 0 = ^Z jew_t P j ⁽r, t) S _p            (10)

Where, S j denotes the workload usage because of instance j. From hour i to hour k, the quantity of workload consumption delayed is noted as:

Q i,k = P^k ,|k-i|)( W_t-w_t) (11)

And also for a given set of rewards and hour shifted time, the shifting workload function depends completely on the variables, у j &  S j where у j is tolerance index. In this we have to now locate similar tolerance index parameters together. As in (10) the similar index has become one which is P j (r,t)S j . Note that W i -w i is the usage demand shifted from hour i.

Let S i show the difference between the usage demand W i without using TDP and the usage demand using TDP. Each S i can be expressed with collective shifting workload function:

Si = Z к ^iQk-Q i,k              (12)

Each S i , where i ss 1,2,3,….n could be stated as a ” ⁽”~ ¹ ) linear functions of S i . Starting from S 1 , S 2 to S_n-1 these n linear equations can be calculated by Q 1,2 ,

Q _2,3, Q _3,4,……., Q _n-1,n. For every, i there is a value of k as stated in this calculation. This linear function is calculated for every day at the providers end and stored in the dataset. Now we can apply the best fit algorithm to calculate the Yj and 6j which determine Q _i,k and give the shifted workload function. Non-linear least square method is used as the best fit algorithm in these calculations. This algorithm can run offline, rather than in real time.

• V.    Simulations

  We simulated this model in CloudSim as cloudlets. More than 3000 cloud workloads were used for these calculations [21]. CloudSim an open source software simulated by different researcher for their research [23]. Here we show the feasibility of this model and devise a method to reduce the providers’ cost optimization problem. We calculate the execution time of workloads with or without using TDP. We also compare other existing scheduling policies with CCTB. Table 4 shows the characteristics of resources that are used in the experimental setup. The performance of this algorithm is done with around 3000 workloads and 50-250 cloud computing resources.

Table 4. CloudSim Parameters and their values

Parameters	Values
Number of resources	50–250
Number of cloudlets (workloads)	3,000
Bandwidth	1,000–3,000 B/S
Size of cloud workload	10,000+ (10–30%) MB
Number of PEs per machine	1
PE ratings	100-4,000 MIPS
Cost per cloud workload	$3-$5
Memory size	2,048–12,576 MB

CloudSim [21] is used to calculate the execution time of each resource. The result shows the performance of the algorithm over other existing policies. Table 4 shows the characteristics of resources and cloudlets that have been used for all the experiments. Consumer cloud workload are modeled as independent parallel applications. Thus the data dependency among the cloud workloads in the parallel applications is negligible. Each cloud workload is parallel and is hence considered to be independent of any other cloud workload.

We compare our scheduling approach with the existing scheduling algorithms, which are: Compromised Time Cost (CTC) [19] and Deadline and Budget DistributionCost Time Optimization (DBD-CTO) [20]. The aggregate of shifting workload function is taken as a sum of function, as in (9), where у = 0.5, 1, 1.5……, 5 (shifting parameters are chosen collectively).

Test Case 1: execution time and cost comparison of cloud workloads with or without using TDP: the execution time for same cloud workload and having same no. of resources is calculated by CloudSim, TDP took 1,321 seconds whereas the flat rate pricing took 1,468 seconds. The execution time in TDP is less than the time taken by flat rate pricing. Fig. 6 shows the result of this evaluation. Fig. 7 shows the cost structure of TDP and flat rate pricing. It cost $195 using TDP whereas $238 using flat rate pricing. The results are calculated using the same number of resources and same workload.

Test Case 2: execution time and cost comparison of cloud workloads using TDP with different Scheduling policies: Fig. 8 and 9 show the result using different scheduling policies with TDP. Execution time and cost for the same number of workloads and same number of resources are calculated differently using scheduling policies. The result shows that CCTB improves the execution time and cost for different workloads. Each scheduling algorithm works with homogenous cloud workloads. These scheduling policies are implemented in CloudSim using VMSchedular.java. Results show that CCTB scheduling policy combined with TDP improves the execution time and cost of cloud computing, which subsequently overcomes service providers’ cost minimization problem and helps the provider to increase their revenue.

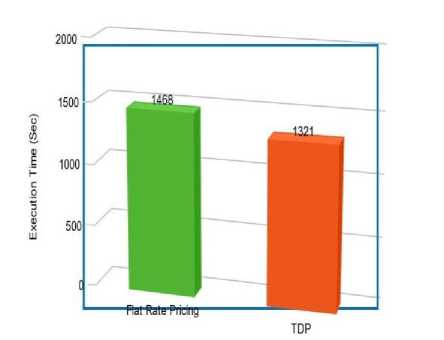
Fig.6. Execution Time Comparison of Same Workload and Same No. Of Resources for Different Pricing Schemes.

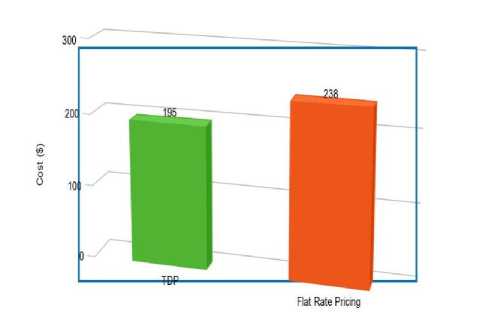
Fig.7. Cost Comparison of Same Workload and Same No. of Resources for Different Pricing Schemes.

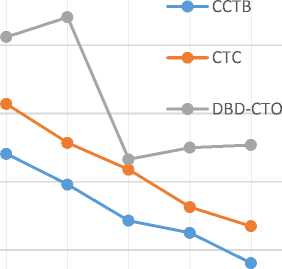
Test Case 3: execution time for different number of resources and cloud workloads using three scheduling policies: Outcome of increasing the resources while keeping the workload constant in CWMS is shown in Fig. 10.The outcome shows that as the resources increase the corresponding time of execution decreases. CCTB performs better than other two scheduling policies. Fig. 10 shows that as the resources increase, execution time decreases in the same proportion in CTC and CCTB. The results of increasing the workload at execution time are shown in Fig. 11. We have approximately 3,000 workloads to show this result. As the outcome states that the execution time reduces using the CCTB policy as compared to other scheduling policies. The average reduction time is around 12-28%. The execution time generally increases with increase in number of workloads. The Fig. 11 results show that CCTB is a better approach than other two.

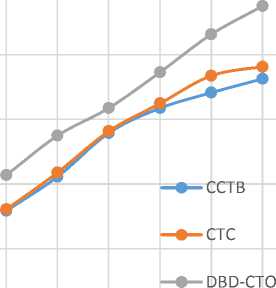
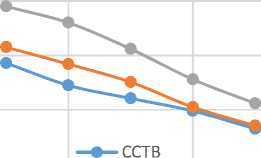
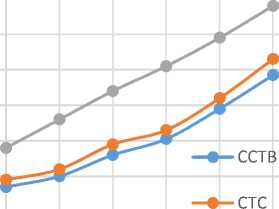
Test Case 4: Cost for different number of resources and cloud workloads using three scheduling policies: The cost for cloud workload execution varies for every scheduling policy. Fig. 12 shows the outcome that the cost of execution decreases with increase in the number of resources. Fig. 12 illustrates that CCTB scheduling policy consumes less cost for the same number of resources as compared to other scheduling policies. Fig. 13 shows that the cost per workload increases as the cloud workload increases for a given constant number of resources. The existing scheduling policies seem to be expensive as compared to the CCTB scheduling policy. The overall cost for handling such amount of cloud workload is less by using the CCTB scheduling policy as compared to CTC and DBO-CTO. CCTB performs better with increase in the number of workloads. Cloud Computing data security is emerging challenge discussed in [22].

The various resulted graph shows the advantage of proposed model over other existing models. This model gives the better execution time and less cost of resources in compare to other existing models. This models is compare with other two existing models proposed in [19] [20]. In this paper we tried to extend our previous work [24] [25].

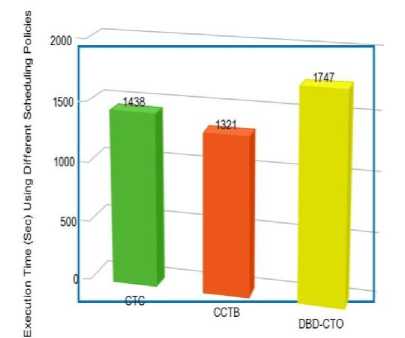
Fig.8. Execution Time Comparison of Same Workload and Same No. Of Resources for Different Scheduling Policies.

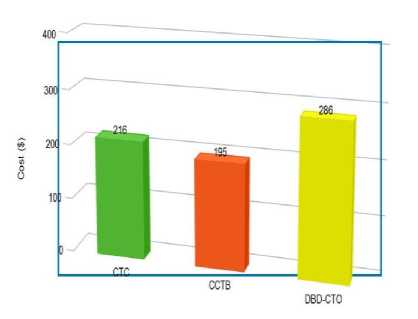
Fig.9. Cost Comparison of Same Workload and Same No. of Resources for Different Scheduling Policies.

OJ СП

E 1500

0     50    100   150   200   250   300

No. of Resources

Fig.10. Execution Time Comparison of Same Number of Workload with Different Number of Resources on Different Scheduling Policies.

E 1500

0   500  1000 1500 2000 2500 3000 3500

No. of cloud workloads

Fig.11. Execution Time Comparison of Same Number of Resources with Different Number of Workload on Different Scheduling Policies.

о

<_>

CTC

—е— DBD-CTO

100          200          300

No. of Resources

Fig.12. Cost Comparison of Same Number of Workload with Different Number of Resources on Different Scheduling Policies.

О 400

4 DBD-CTO

0   500  1000 1500 2000 2500 3000 3500

No. of cloud workloads

Fig.13. Cost Comparison of Same Number of Resources with Different Number of Workload on Different Scheduling Policies.

• VI.    Conclusion

This paper works on the aspects of smart cloud computing and introduces an economic model using TDP. We model consumers’ willingness to transfer their workloads to lower price off-peak hours. We express a need of cost minimization to providers’ optimization problem. The architecture of our framework is a feedback loop between consumers and service providers with workload management system and real time scheduling using CCTB. Results show that improved prices helps service provider to increase their revenue.

Acknowledgment

We would like to thank Mr. Sukhpal Singh, Mr. Aashish Jainani, Mr. Ansh Juneja, Mr. Amir Mussanna, Ms. Anita Chauhan and Ms. Ritu from Thapar University, Patiala for helping us improve expression and language of this paper.