Децентрализованное управление финансовыми потоками в региональных иерархических системах

Процессы принятия и реализации решений в региональных иерархических системах обычно ассоциируются с централизованным управлением. Данный тип организации управления в экономической сфере сохраняет существенное значение как на макроуровне, где он соответствует государственному регулированию экономики и межгосударственным структурам, так и на мезоуровне регионального управления.

Стремление руководителей регионов повысить эффективность управления, управляемость экономическими процессами в регионе, согласованность решений и координации действий обычно связывают, как средство, с усилением центральной власти, концентрацией полномочий, усилением регламентов и контрольных функций региональной власти.

Централизованному управлению мы противопоставляем самоорганизацию региональных экономических систем, которая наиболее ярко проявляется в теории монетаризма. Процессы самоорганизации являются достаточно сложными и противоречивыми, и их положительные эффекты связаны со стимулированием актив- ности наиболее значимых в регионе субъектов экономической деятельности, с устойчивостью функционирования крупных налогоплательщиков и с эффективным, творческим участием руководителей таких организаций в мезоэкономике.

Проблема синтеза региональной иерархии и самоорганизации находит свое выражение в децентрализованном управлении регионом, при котором возникает спектр организаций (муниципальных образований, предприятий, учреждений и т.д.), различающихся уровнем децентрализации. Исследование децентрализованного управления регионом является актуальной задачей, а ее постановка представляет определенные сложности.

В данной работе мы методически исходим от идеи «ослабления» централизованного управления регионом в противоположность подходу «от самоорганизации к усилению роли центра». Этот подход наиболее соответствует возможностям декомпозиционных методов и моделей, используемых нами для исследования иерархических систем.

Рис. 1. Взаимосвязи центров принятия решений в децентрализованной иерархической

системе региона

На примере иерархической системы, схематическое описание которой приведено на ри- сунке 1, рассматриваются организация, условия и процесс разделенного принятия реше- ний совокупностью (n + 1) лиц, принимающих решение (ЛПР) в региональной системе. В рассматриваемом примере роль верхнего уровня играет центр, а нижний уровень представлен муниципальными образованиями МО i и бизнес-единицами БЕj. Автономное функционирование выделенных экономических субъектов возможно после формирования для них самостоятельных задач принятия решений, так чтобы выполнялись определенные условия оптимальности системы в целом.

Конечным итогом моделирования иерархических систем региона является построение адекватной реальности совокупности математических задач принятия эффективных решений для выделенных субъектов управления.

Адекватность, эффективность и оптимальность. Термины «адекватность» и «эффективность» используются по содержанию в соответствии с работой Г.Б. Клейнера [1] как главные характеристики качества экономико-математической модели. При этом адекватность отражает соответствие модели региональным процессам, а эффективность - возможность применения модели на практике, т.е. в смысле экономической эффективности нового проекта системы управления регионом. Таким образом, «адекватность» и «эффективность» - понятия, которые характеризуют разные отношения и не сводятся друг к другу.

Структура математической модели децентрализованного управления регионом приведена на рисунке 2. Далее считаем, что центр изменяет часть переменных состояния системы $ ц при допустимом множестве S_ц , зная условия управления f , т.е. имеется часть неуправляемых внешних и внутренних факторов. Аналогично ЛПР_: изменяет состояние части системы s . из множества S . , зная параметры f . Такое же описание имеет ЛПР_j .

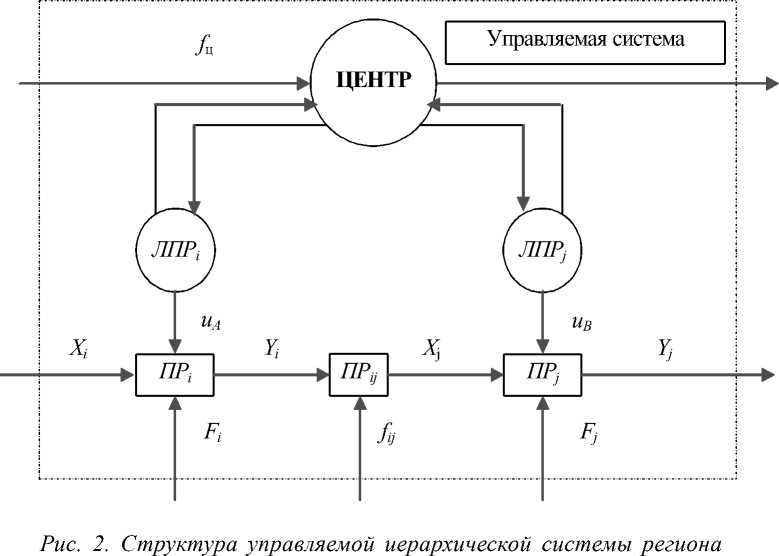
Характер горизонтальных связей соответствует процессу ПР_у взаимодействия муниципальных образований МО . и бизнес-единиц БЕ j . Ниже рассматриваются также состояния s системы в целом и совокупность условий f, соответствие которых описанию регионального центра, муниципальных образований и бизнес-единиц устанавливается в процессе моделирования.

Одним из главных условий адекватности модели является информированность ЛПР. Информированность считается одинаковой, если совпадают информированности центра/ц, муниципальных образований f i, бизнес-единиц fj, и полной, если они равны f Информированность является асимметричной, если равенства fЦ=f ‘ = f нарушаются. При децентрализованном управлении регионом имеет место, как правило, асимметрия информированности элементов региональной управляемой системы.

В работе [2] развивается двухэтапный подход к моделированию (этап 1 - построение формальной иерархической системы, этап 2 - конкретизация условий выбора решения выделенных ЛПР), в соответствии с которым ниже рассмотрим лишь проблемы этапа 1. Указанное разделение задачи моделирования имеет, на наш взгляд, прямое соответствие реальному функционированию региональных управляемых систем, в котором, как известно, выделяются планирование и реализация планов. Региональная управляемая система может иметь иерархическую структуру при согласовании плановых решений и одноуровневую структуру при их исполнении. В экономике можно указать и случаи, когда региональная иерархическая структура возникает только в период реализации плана. Следует также различать наличие «фиктивной региональной иерархии», которая возникает как способ принятия решений верхним уровнем (центром), например, при использовании методов декомпозиции в качестве расчетного средства. Перечисленные и связанные с рассмотренными проблемы выделим как проблемы адекватности ЭММ 1 (напомним, что адекватность характеризует отношение модели к объекту моделирования ).

Одной из принципиальных проблем моделирования иерархических систем является оценка эффективности (работоспособности) моделей, т.е. возможность использования для решения конкретных управленческих задач. Трудность анализа состоит в том, что данный аспект моделирования иерархических систем в литературе рассмотрен недостаточно полно. Мы придерживаемся рекомендаций ученых, которые предлагают в данном случае использовать подходы к оценке эффективности экономических проектов, т.е. выделять базовые значения показателей эффективности экономической системы, затем рассматривать эти показатели при использовании в процессе принятия решений математических моделей, а затем получить оценку эффективности использования математических моделей по приросту указанных показателей. Такой подход использован, в частности, в работе [3] при оценке ущерба, упущенной выгоды и полезного эффекта, связанного с деятель ностью менеджеров, и может быть применен для оценки деятельности руководителей регионов, муниципалитетов, организаций.

В конечном итоге для оценки эффективности решений руководителей, с точки зрения системы в целом, необходимым элементом моделирования является установление показателя эффективности региональной системы. Обозначим этот показатель I_c (s). В простейшем случае считаем, что I c - скалярная функция. Пусть 1 с ^н -пороговое значение показателя. Модель считаем эффективной, если для конкретной региональной системы s * выполняется неравенство

Современные теории экономико-математического моделирования широко используют понятие оптимальности решений, поэтому необходимо установить отношения оптимальности и эффективности. Некоторые авторы не акцентируют внимание на различиях категорий оптимальности и эффективности, считая, что оптимальные решения по определению являются эффективными. При этом игнорируется то, что оптимальность определяется как «наилучший способ экономического поведения, возможность или способность достигнуть оптимума, оптимального значения чего-либо» [4] в заданных условиях выбора решений.

Наиболее близкими к нашей позиции являются взгляды авторов работ [5-7], суть которых сводится к тому, что оптимальные решения могут быть неэффективными. Оптимальные решения, т.е. решения, «лучшие из ...», будут эффективными, например, в том случае, когда среди допустимых состояний системы имеются состояния, для которых вышеприведенное неравенство выполнено, а в качестве целевой функции задачи выбора решений используется показатель эффективности 1 с (s) .

Принцип оптимальности можно использовать и в том случае, когда оптимальное решение не является эффективным. Анализ математических условий, например, с использованием методов оценки чувствительности [8], позволяет привлечь дополнительные ресурсы, или изменить цели, обеспечив необходимый уровень эффективности решений, или обосновать нецелесообразность вмешательства в существующий процесс функционирования региональной управляемой системы. Таким образом, в дальнейшем будем рассматривать задачу выбора оптимальных решений для региональной управляемой системы в целом, общая запись которой имеет вид:

1 с (s*) = max I_c(s),    s e S,         (1)

где S - множество допустимых состояний региональной управляемой системы.

Таким образом, для оценки эффективности решений, полученных совокупностью ЛПР, необходимо ввести в рассмотрение новую задачу (1) и, соответственно, новый элемент моделирования региональных иерархических систем. Заметим, что не во всех существующих подходах математического моделирования используется системная задача (1), в частности, в теории игр большинством авторов эта задача не рассматривается. Как примеры исключения приведем работы [2, 3], где задача центра отождествляется с задачей (1). Представляет интерес и подход в теории игр, выраженной цитатой:«... в дальнейшем мы будем вести рассмотрение событий с позиций абстрактного наблюдателя» [9]. В декомпозиционном подходе системная задача (типа (1)) играет исключительную роль как основа построения системы задач всех выделенных ЛПР и как средство оценки их эффективности. Для обозначения системной задачи (1) мы (следуя [10]) используем в ряде случаев термин «глобальная задача». Следует отметить, что в корпоративных структурах субъектом экономики, интересы которого представлены задачей (1), выступают собственники при рассмотрении компании в целом или вышестоящие менеджеры при моделировании частей иерархической системы. В этом контексте моделирования процессов принятия решений совокупностью ЛПР рассмотрение задачи (1) становится адекватным экономическим отношениям субъ ектов реальных систем.

Рассмотрим далее вопросы организации, устройства распределенного принципа принятия решений согласно существующим теориям иерархических систем.

При моделировании наряду с задачей (1), которую обозначим:

C3 = < S, I_c (s) >  необходимо получить задачи:

Зц = < Sц, 1ц (s) >; ЗЛПР. = < S, I. (s) >; ЗЛПР . = < S j , I j ()) > .

Принцип разделения управляющих воздействий между ЛПР, характер внутриуровнево го, межуровневого взаимодействия в системе, асимметрия информированностей, регламенты функционирования элементов и другие аспекты организации управляемой иерархической системы в обзорно-аналитическом плане рассмотрены, например, в работе [5]. В данной статье остановимся на двух аспектах: согласование интересов ЛПР, что выражается в выборе вида функций 1ц, I, I. и их соответствии функции 1с и в неизбежной для региональных иерархических систем асимметрии информированности выделенных ЛПР.

Процессы формирования интересов субъектов экономической деятельности и их отражение в математических моделях относятся к числу наиболее сложных, многоаспектных. Дискуссии по проблемам согласования интересов, по принципам экономического поведения людей постоянно проводятся в научной литературе и, по нашему мнению, далеки от их завершения. Для нашего исследования особый интерес представляет анализ критики декомпозиционного подхода, суть которой сводится к тому, что задачи ЛПР (в нашем случае Зц, ЗЛПР, ЗЛПР . ), полученные декомпозицией системой задачи (в нашем случае (1)), не соответствуют реальным целевым установкам субъектов экономики. Объектом критики декомпозиционного подхода выступает в данном случае способ внешнего к объектам «назначения» целевых установок (см., например, [10-12]).

Диаметрально противоположным является теоретико-игровой подход к описанию интересов и процессов взаимодействия совокупности ЛПР в экономических системах. В этом случае описание задач ЛПР осуществляется «свободно», без ориентации на системные цели, как отражение индивидуальных или групповых интересов, преследуемых выделенными субъектами деятельности. Таким образом, мы переводим суть проблемы формирования целевых интересов ЛПР к экономической сущности поведения субъектов реальной экономики, оставляя пока в стороне способ описания этих интересов.

Подведем некоторые итоги исследования проблем моделирования децентрализованного процесса принятия решений в региональных иерархических системах. Основными, качественными показателями процесса моделирования выступают адекватность и эффективность полученной системы моделей. При этом прин- цип оптимальности в общем случае не обеспечивает требование эффективности моделей. При моделировании децентрализованного управления регионом определена функция и показана необходимость использования системной модели оптимизации (глобальной задачи регионального упр авления). Это обстоятельство выступает объективным основанием для применения декомпозиционного подхода [13–16] при исследовании и организационном проектировании децентрализованных иерархических систем управления регионом. Вместе с тем, может быть выделен класс ролевых систем, для которых при наличии механизма стабилизации ролевого поведения наиболее значимых для региона субъектов экономической деятельности могут быть применены декомпозиционные методы и модели системных задач управления регионом. При применении декомпозиционного подхода может выделяться методическая функция, которую выполняет система задач, полученная формальной декомпозицией глобальной задачи регионального управления. В терминах формальной декомпозиции могут быть описаны процессы раздельного выбора решений в региональных системах с полной информацией, в системах неполной, но совпадающей информированности наиболее значимых для региона субъектов экономической деятельности и в условиях асимметрии в информированности центра и субъектов. Показана необходимость адекватной реальной информированности постановки и декомпозиции системной задачи регионального управления. Данная проблема требует дополнительных исследований как в общетеоретическом аспекте, так и в вариантах реального разделения управляющих решений в децентрализованных региональных системах управления.

• 1.    Клейнер Г.Б. Экономико-математическое моделирование и экономическая теория // Экономика и математические методы. 2001. №3. Т. 37. С. 111–126.

• 2.    Мамченко О.П. Потоковые модели систем управления корпоративной организацией: монография. Барнаул, 2002.

• 3.    Мамченко О.П., Кабаев С.И., Толстов В.К., Рязанов М.А. Модель функционирования производственной системы при децентрализованном управлении // Известия Алтайского государственного университета. 2001. №1. С. 57–60.

• 4.    Большой экономический словарь / под ред. А.Н. Азрилияна. 2-е изд., доп. и перераб. M., 1997. С. 405.

• 5.    Алгазин Г.И. Математические модели системного компромисса: монография. Барнаул, 1999.

• 6.    Гермейер Ю.Б. Игры с непротивоположными интересами. М., 1976.

• 7.    Горелик В.А., Кононенко А.Ф. Теоретико-игровые модели принятия решений в эколого-экономических системах. M., 1982.

• 8.    Таха Х. Введение в исследование операций: в 2 кн. Кн. 2 / пер. с англ. М., 1985.

• 9.    Ерешко Ф.И. Моделирование рефлексивных стратегий в управляемых системах. M., 2001. С. 9.

• 10.    Месарович М., Мако Д., Такахара И. Теория иерархических многоуровневых систем. М., 1973.

• 11.    Первозванский А.А. Предисловие к книге Лэздона «Оптимизация больших систем». М., 1975.

• 12.    Багриновский К.А. Основы согласования плановых решений. М., 1977.

• 13.    Оскорбин Н.М. О схемах блочного программирования // Экономика и математические методы. 1981. №5.

• 14.    Лэсдон Дж. Оптимизация больших систем. М., 1975.

• 15.    Цурков В.И. Декомпозиция в задачах большой размерности. М., 1981.

• 16.    Первозванский А.А., Гайцгори В.Г. Д екомпозиция, агрегирование и приближенная оптимизация. М., 1980.