Децентрализованные алгоритмы обработки информации в двухканальных измерительных системах

Задача обеспечения высокой точности оценивания координат и параметров траектории движения объекта может быть решена за счет применения многоканальных измерительных систем с оптимальной централизованной обработкой [1]. Алгоритмы оптимальной многоканальной калмановской фильтрации предполагают объединение в пункте обработки информации (ПОИ) оценок векторов наблюдаемых параметров, рассчитанных в измерительных пунктах.

Централизованной обработке присущи следующие недостатки [2]:

• -    необходимость передачи с измерительных пунктов в пункт обработки информации всего объема получаемой информации;

• -    большой объем вычислительных операций в пункте обработки информации для определения координат и параметров траектории цели;

• -    необходимость предварительного приведения оценок измерительных пунктов к единой системе координат и др.

Для устранения этих недостатков представляется целесообразным предусмотреть фильтрацию оценок текущих траекторных измерений в измерительных пунктах. Применение фильтрации координатной информации в измерительных пунктах позволит в случае неисправности системы обработки в одном или нескольких из этих пунктов производить оценивание координат объекта с относительно высокими точностными характеристиками.

В работе производится сравнительный анализ эффективности функционирования двух систем децентрализованной обработки информации. В измерительных пунктах применяются алгоритмы фильтрации Калмана.

В первом алгоритме обработки результаты оценок векторов состояния, рассчитанных в измерительных пунктах, комплексируются в ПОИ (Ф-О-алгоритм). Во втором алгоритме в ПОИ осуществляется их фильтрация (Ф-Ф-алгоритм).

Ввиду того что оценки векторов состояния первого ( а 1 ) и второго пунктов ( а 2 ) независимы, то для синтеза алгоритма, основанного на алгоритме комплексирования соответствующих оценок а 1 и а ₂ в ПОИ, используем методику, приведенную в [3].

Оценки а. 1 и а ₂ на выходе измерительных пунктов имеют нормальный закон распределения [3] n 1

p (а) = (2л) ²| C , |2exp [ ^- (а ^- а , ) T С , (а ^- а , )/2 ^{], (1)} где а - оцениваемый случайный вектор состояния; С_р С ₂ -симметричные матрицы точности соответственно для первого ( i = 1) и второго ( i = 2) измерительных пунктов ( i = 1,2).

Найдем выражение логарифма совместной плотности вероятности:

ln p (Й 1 , а₂) = - (1/2)(а - (1 1 ) T С 1 (а - (1 1 ) -

• - (1/2)а - а2) TC 2(а - а2) + const.(2)

Преобразуем (2) и, изменяя постоянную, получим lnp(11, а2) = -(1/2)аT (С1 + С2)а + (1/ 2)аT (С161 +

+ С 2а2) + (1/2)( С 1(11 + С 212)а + const.(3)

Введем матрицу

Сp = С1 + С2

и вектор-столбец

Cp а p = С1а1 + С 2а2.(5)

Как и матрицы С1 = QT, С2 = С2T, матрица (4) обладает свойствами симметрии: Cp = Ср . Транспонируя (5), получаем T  TT а Cp = а, С1 + а 2 С 2.               (6)

В силу (4), (5), выражение (3) после изменения постоянной принимает вид ln p(а1, а2) =-(1/2)(а - аp)T Ср (а - аp) + const. (7)

Определяя отсюда плотность вероятности p (а 1 , а₂) ипо-стоянную (7) по условию нормировки, приходим к стандартной форме записи многомерного нормального закона:

• - П      1

p (ф,« 2 ) = (^{2 л} ) ² ^ p ²exp ^[- (1^/2)(а ^- a p ) T ^ (а ^- а p ) ] ■ W

Оценка а _p соответствует максимуму послеопытной плотности вероятности p (« 1 , а₂) . Она оптимальна по критерию минимума как при квадратичной, так и при простой функции стоимости.

Вычисление результирующей матрицы точности сводится, согласно (4), к суммированию матриц точности С 1 и С ₂. Результирующая корреляционная матрица ошибок C _p ^{- 1} получается путем обращения результирующей матрицы точности C _p .

Результирующая оценка вектора состояния а _p сводится к весовой сумме оценок а 1 и а ₂.

Произведем синтез Ф-Ф-алгоритма, который основывается на фильтрации в ПОИ оценок 6.1 k и а ₂ k , полученных в результате вторичной обработки в измерительных пунктах ( к- номер такта измерения).

Результирующую оценку вектора состояния 1 _pk , рассчитанную в ПОИ, получим на основе алгоритмов фильтрации Калмана [3]:

a pk = a k / k-i + Kk 1^ k - hk («k / k-1)1

C-1 pk = C-1 k/k-i - KkHkC-1 k/k-i,(11)

K k = C ^{- 1} k / k - 1 H_k T (H_kC ^{- 1} k / k - 1 H_k ^T + C ^-м) ^- 1 , (12)

C-1 k / k-1 = Bk-1C-1 k-1 BTk-1 + Qk-1,(13)

где a _k / _k 1 = B_k - 1 a _k 1 - прогнозированная оценка вектора состояния; K_k - матричный коэффициент усиления; X _k = (a ^T 1 k , a ^T 2 k ) T - оценка вектора наблюдаемых параметров на входе ПОИ; h_k (a _k , _{k - 1}) - прогнозированная оценка вектора наблюдаемых параметров; H _k , B_k , Q_k - известные матрицы.

Покажем схему алгоритма децентрализованной обработки информации в двухканальной измерительной системе (рис. 1).

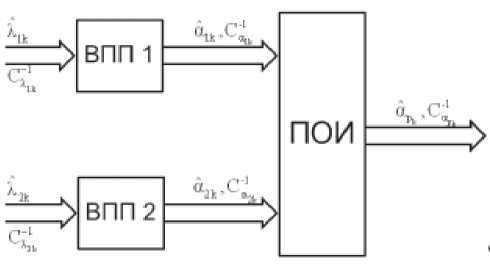
Рис. 1. Структурная схема децентрализованной системы обработки координатной информации

Элементы вектора состояния ct ik представляют собой оценки координат объекта и оценки скорости их изменения в декартовой системе координат. Фильтрация оценок вектора состояния в пункте обработки информации может также производиться в декартовой системе координат. В данном случае блочная матрица статического пересчета Н имеет следующую структуру:

H =

(дХ ^{( 1 )} )

( j )

<, I T ) T

где I- единичная матрица.

Корреляционная матрица ошибок текущего оценивания C-k имеет блочную структуру и в силу независимости и одновременности измерений в измерительных пун ктах определяется выражением

( с ^{- 1} 0 '

^сч = _ok _с-1 .                   (15)

V ^{0 C}2k )

Матричный коэффициент усиления Kk после подстановки в формулу (12) соотношений (14), (15) преобразу ется к виду

- / X                       /     -.              \~1 -1

K k = C- ( I, I )! C -K ( I, I ) + C ^{k 0}

-V I )             V ^{0    C}2 k )_

После проведенных математических выражение для матричного коэффициента усиления K принимает вид

K k = ( K 11 k ,K 12 k ) ,                 (17)

где K11 k, K12 k - матричные коэффициенты усиления соот ветственно для первого и второго измерительных пунктов.

Результирующая корреляционная матрица ошибок измерений определяется как c-1 = C-1 - KllkC;1 =11 - Kllk c-1      (is)

k         3K            1 IK ЭК                    11K 3K .

1 = 1                     V        1 = 1           )

Результирующая оценка вектора состояния ak с уче- том (16) имеет вид

« k = « эк + ^{+ ( K} 11 k ,^K 12 к )

« 1k

« 2k

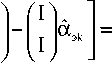
^^^^^^в

« эк

^^^^^^в

« эк

= « эк ^{+ ( K} 11 к ,^K 12 к )

Г -.

“ ^1k

-« 2k

.

В более компактной форме выражение (19) можно представить в виде 2

« k =« эк ⁺ £ K ilk ( « 1к ^-« эк ) .       (2°)

В экстраполяторе результирующая оценка вектора состояния, сформированная в ПОИ, прогнозируется на следующий такт измерения. Невязка v1k = a1k -aзк, рас считанная в каждом из измерительных пунктов приема, с установленным матричным весом добавляется к прогнозированной оценке, что и дает результирующую оценку вектора состояния [3].

Алгоритм упрощенного фильтра Калмана (УФК), в оценке вектора состояния которого присутствуют оценка координат и скорости их изменении, называют УФК-алгоритмом, а алгоритм расширенного фильтра Калмана (РФК), в оценке вектора состояния которого имеется и оценка ускорения, - РФК-алгоритмом.

Рассмотрим следующие модификации фильтров сопровождения в декартовой системе координат:

• -    фильтрация в вынесенном приемном пункте (ВПП), УФК-фильтр + фильтрация в ПОИ, УФК-фильтр (УФК-УФК-алгоритм);

• -    фильтрация в ВПП, УФК-фильтр + фильтрация в ПОИ, РФК-фильтр (УФК-РФК-алгоритм);

• -    фильтрация в ВПП, РФК-фильтр + фильтрация в ПОИ, УФК-фильтр (РФК-УФК-алгоритм);

• -    фильтрация в ВПП, РФК-фильтр + фильтрация в ПОИ, РФК-фильтр (РФК-РФК-алгоритм).

Результаты имитационного моделирования приведены в виде графической зависимости среднеквадратической ошибки O x и ошибок оценивания A x в метрах от номера такта измерения к для одной декартовой координаты X . Для двух других координат (У и Z ) результаты аналогичны.

Для полного анализа достаточно исследовать качество фильтрации оценок координат объекта при двух траекториях его движения:

• -    равномерном прямолинейном движении объекта в направлении на радиолокационную службу для выявления потенциальных возможностей;

• -    движением по окружности с заданной перегрузкой для выявления возможностей сопровождения маневрирующих объектов.

Рассмотрим качество фильтрации каждого алгоритма на этапе равномерного прямолинейного движения. Представив зависимости среднеквадратичной ошибки (СКО) и ошибки оценивания координатыАв метрах от такта изме рения для всех предлагаемых к исследованию алгоритмов сопровождения (рис. 2). УФК-УФК-алгоритму соответствует кривая 1, РФК-РФК-алгоритму - кривая 2, УФК-РФК-алгоритму - кривая 3, РФК-УФК-алгоритму - кривая 4. Анализ приведенных графиков показывает, что УФК-УФК-алгоритм при слежении за неманеврирующим объектом имеет преимущество в точности сопровождения, СКО оценивания в 1,5 раза меньше СКО алгоритмов, основанных на расширенных фильтрах Калмана. РФК-РФК-алго-ритм имеет максимальные среднеквадратические ошибки. Это объясняется тем, что при сопровождении объекта, движущегося равномерно и прямолинейно в декартовой системе координат, учет второй производной (ускорения) в векторе состояния приводит к увеличению ошибок оценивания. УФК-РФК-алгоритм имеет результаты фильтрации оценок координат, сравнимые с УФК-УФК-алгорит-мом. Это указывает на то, что применение в приемных пунктах фильтров с упрощенным вектором состояния позволяет получать высокие точности оценивания вектора состояния при сопровождении объектов с прямолинейной равномерной траекторией движения. РФК-УФК-ал-горитм занимает промежуточное положение среди анализируемых алгоритмов.

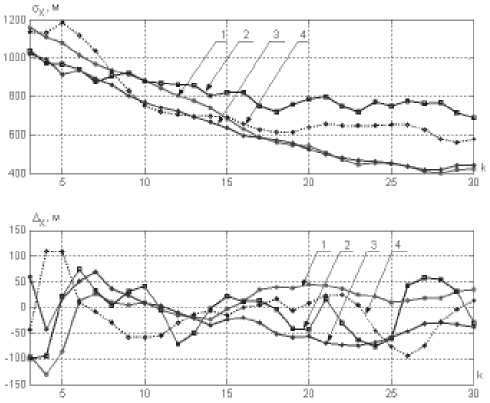
Рис. 2. Зависимость СКО О и ошибок оценивания А xx координаты х для прямолинейного движения для модификаций УФК и РФК алгоритмов сопровождения

Таким образом, среднеквадратическая ошибка для УФК-УФК-алгоритма к десятому шагу фильтрации уменьшается в 1,2 раза, к двадцатому шагу - в два раза. Для модификации РФК-РФК результаты следующие: к десятому шагу фильтрации СКО уменьшается в 1,2 раза, а к двадцатому - в 1,4 раза. Иными словами, до десятого шага фильтрации результаты практически одинаковые, а потом фильтры сопровождения с упрощенным вектором состояния имеют значительный выигрыш в точности оценивания вектора состояния.

Работа рассматриваемых алгоритмов сопровождения имеет ряд особенностей. При сопровождении объектов используется несколько фильтров Калмана (см. рис. 1). Каждый из фильтров можно настраивать, учитывая особенности внешних и внутренних факторов, влияющих на точность оценивания. Основным элементом управления в фильтре Калмана является матрица дискретного маневра Qk, физический смысл которой заключается в регулировании полосы пропускания фильтра. Необходимо выбрать такой нижний порог полосы пропускания фильтра, который позволит с минимальными ошибками оценивать координаты объекта и при этом не будет наблюдаться процесс расходимости фильтра. Если полоса пропус кания фильтра уменьшается, то фильтр при поступлении обновляющей информации начинает слабо реагировать на нее и в этом случае основной вес в результирующей оценке имеет прогнозированное значение оцениваемого параметра. Чрезмерное уменьшение полосы пропускания приводит к тому, что фильтр практически полностью доверяет прогнозированному значению, не принимая во внимание обновляющую информацию. В этом случае может наблюдаться процесс расходимости фильтра сопровождения, заключающийся в увеличении ошибок оценивания. В случае если ошибки оценивания значительно превышают ошибки первичных измерений, то речь идет о срыве сопровождения объекта.

Проведем анализ влияния полосы пропускания на качество фильтрации результирующей оценки вектора состояния на выходе ПОИ.

Данный анализ целесообразно провести при движении объекта по дуге окружности. Если полоса пропускания не адекватна протекающим процессам, то должно наблюдаться увеличение среднеквадратических ошибок оценивания координат объекта. Ширина полосы пропус кания регулировалась путем изменения величины элементов матрицы дискретного маневра Qfc на два порядка. Необходимо отметить, что при моделировании изменялась полоса пропускания только того фильтра сопровождения, который используется в пункте обработки, в измерительных же пунктах ширина полосы пропускания фильтров оставалась неизменной.

Зависимости СКО и ошибок оценивания координаты X объекта при движении по окружности с перегрузкой, равной двум, приведены на рис. 3. Кривая 1 соответствует УФК-УФК-алгоритму с узкой полосой пропускания, кривая 2 - УФК-УФК-алгоритму с широкой полосой пропускания, кривая 3 - РФК-РФК-алгоритму с узкой полосой пропускания, кривая 4 - РФК-РФК-алгоритму с широкой полосой пропускания. УФК-УФК-алгоритм с узкой полосой пропускания имеет большие ошибки оценивания в момент маневра объекта, причем эти ошибки почти в два раза выше ошибок измерения первичных координат. При увеличении полосы пропускания ошибки оценивания уменьшаются и срыва сопровождения объекта не наблю-

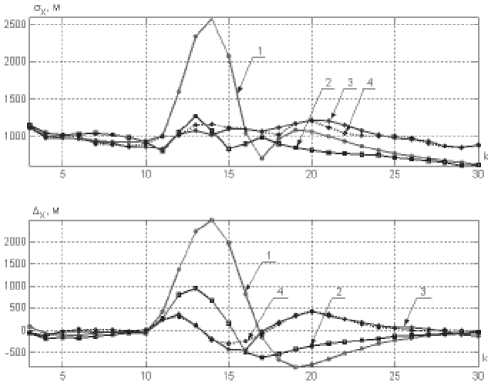
Рис. 3. Зависимость СКО Ox и ошибок оценивания А v координаты х при движении x по окружности с перегрузкой, равной двум дается. В случае использования РФК-РФК-алгоритма резкого увеличения ошибок оценивания не бывает в обоих случаях. Следует отметить, что данный алгоритм имеет высокие точностные характеристики при изменении полосы пропускания фильтра в широком диапазоне.

Кривые 3 и 4 (см. рис. 3) показывают, что ширина полосы пропускания фильтра в пункте обработки информации практически не влияет на точностные характеристики при сопровождении равномерно прямолинейно движущегося объекта, в силу этого обстоятельства примем полосу пропускания фильтра Калмана в пункте обработки широкой для всех предлагаемых к исследованию алгоритмов.

Анализ точностных характеристик алгоритмов сопровождения при движении объекта по окружности производился с перегрузкой, равной шести (рис. 4). На нем представлены зависимости СКО и ошибок оценивания от номера шага фильтрации к для УФК-УФК-алгоритма (кривая 1), УФК-РФК-алгоритма (кривая 2), РФК-УФК-алгоритма (кривая 3) и РФК-РФК-алгоритма (кривая 4). РФК-УФК и РФК-РФК-алгоритмы имеют лучшие точностные характеристики на участке маневра, однако при прямолинейном равномерном движении их СКО намного больше, СКО УФК-УФК и УФК-РФК-алгоритмов. Ошибка оценивания координаты х РФК-РФК-алгоритма в момент маневра составляет всего 250...300 м, в то время как остальные алгоритмы сопровождения имеют ошибки оценивания координаты объекта порядка 800...1 000 м. После окончания маневра через 7...10 тактов измерения среднеквадратические ошибки приближаются к СКО в установившемся режиме.

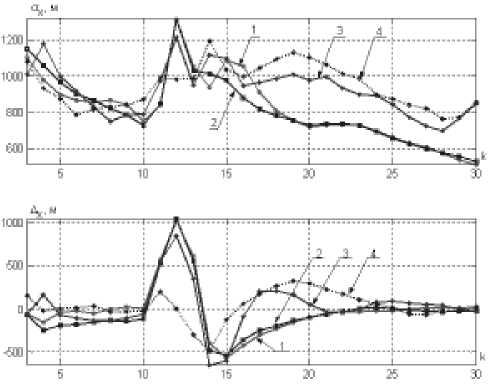
Рис. 4. Зависимость СКО O x и ошибок оценивания A x координаты х при движении по окружности с перегрузкой, равной шести

Рассмотрим результаты моделирования для случая, когда в измерительных пунктах осуществляется фильтрация оценок вектора состояния объекта РФК-фильтрами, а в пункте обработки проводится комплексирование полученной от измерительных пунктов информации. Параметры фильтров в измерительных пунктах идентичны. Представим зависимость СКО и ошибки оценивания координа-ты А объекта при прямолинейном равномерном движении от номера такта измерения (рис. 5), причем кривая 1

соответствует комплексированию информации в ПОИ, а кривая 2 - обработке оценок вектора состояния объекта на основе алгоритмов фильтрации Калмана в ПОИ.

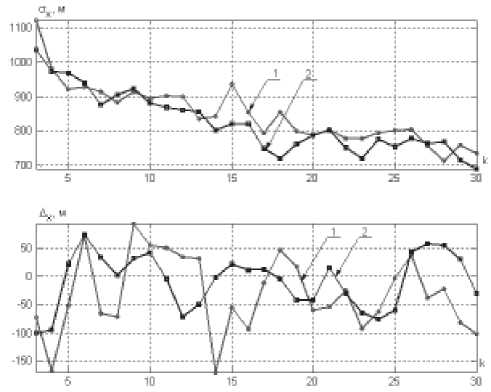
Рис. 5. Зависимость СКО O x и ошибок оценивания A x координаты х при прямолинейном равномерном движении для Ф-О и Ф-Ф-алгоритмов (20)

Результаты фильтрации оценок координаты А практически одинаковы для обоих алгоритмов обработки. Среднеквадратическая ошибка к десятому шагу уменьшается в 1,22 раза, а к двадцатому-в 1,37раза. Ошибки оценивания при фильтрации оценок вектора состояния объекта в пункте обработки информации изменяются более плавно, чем в случае их комплексирования.

Результаты фильтрации оценок координатыАпри движении объекта по дуге окружности с перегрузкой, равной шести, представлены на рис. 6. Кривая 1 соответствует комплексированию информации, полученной от измерительных пунктов, кривая 2 - фильтрации в пункте обработки информации.

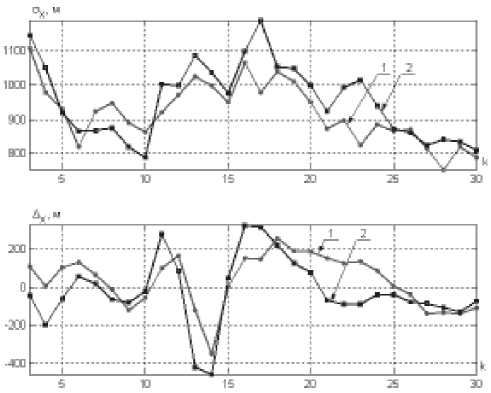
Рис. 6. Зависимость СКО O и ошибок оценивания A xx координаты х при движении по окружности для Ф-О и Ф-Ф-алгоритмов (20)

В заключение можно сделать следующие выводы:

• -    анализ результатов моделирования функционирования УФК-УФК, УФК-РФК, РФК-УФК, РФК-РФК-алго-ритмов показывает, что при прямолинейном равномер-

• ном движении рекомендуется применять УФК-УФК-ал-горитм, при маневре - РФК-РФК-алгоритм;

• -    среднеквадратичные ошибки при фильтрации в ПОИ оценок вектора состояния маневрирующего объекта соизмеримы с соответствующими СКО измерений. Кроме того, ошибки оценивания при маневрировании объекта в результате фильтрации оценок в ПОИ в 1,2 раза больше, чем в случае комплексирования оценок, а Ф-О-алгоритм требует значительно меньшей производительности вычислительных средств.

Таким образом при децентрализованной вторичной обработке информации в двухканальной измерительной системе целесообразно применять алгоритм комплексирования в ПОИ оценок векторов состояния измеритель ных пунктов, рассчитанных с применением алгоритма фильтрации Калмана.