Deep purification technogenic solutions of nickel ions (II) by the modified aluminosilicate

The purpose of this work is to study the possible extraction of ions Ni (II) from aqueous solutions using modified aluminosilicates Eastern Transbaikalia.

Experiment

As object of research there used natural aluminosilicates Eastern Transbaikalia. In the experiments there used the pre-screened on a sieve fraction size of 1,0 mm. Polymers for modification of natural aluminosilicate: poly-1-vinylimidazole (PVIM) and poly-4-vinylpyridine (PVP) were received with binary radical polymerization according to the method [8]. To 1 g of the aluminosilicate was added 1 g of polymer, 18 ml of ethanol. The resulting mixture was stirred for 6 hours at 20 °C on an electromagnetic stirrer. After this time the aluminosilicate was separated from the solution by filtration, washed with water and ethanol, dried oven dried at 100 °C for 2 hours. The resulting product was weighed, the weight gain was calculated. In the process of modifying a polymer consolidation occurs on the surface of the aluminosilicate.

The presence of characteristic of natural and modified aluminosilicate structural groups was confirmed by IR spectroscopy. IR spectra were obtained on a spectrophotometer "Specord 75IR".

In the IR spectra of modified aluminosilicates manifested intense absorption bands in the region 794 and 727 cm-1, characteristic for stretching vibrations of when Al-O. The intense absorption band of 1040 cm-1 corresponds to asymmetric stretching vibrations of the relations Si-O-Si. The absorption band of 3441 cm-1 confirms the presence of communications O-H. There is a shift characteristic absorption bands of the pyridine nitrogen atom in the high frequency region from 1596 to 1601 cm-1, azole cycle from 1508 to 1497 cm-1.

The study of adsorptive properties of the modified aluminosilicate in relation to the heavy metal ions was carried out on the model solutions prepared from reagents qualification "chemically pure": NiSO4·7H2O; and distillized led water.

Selecting the the initial concentration of model solutions substantiated the real composition of industrial waste water. The content of nickel ion (II) in solution determined the by standard techniques [9, 10].

The absorption capacity under study aluminosilicates was studied by static method. In the method of the batches of constant (1 g) and varying concentrations (from 5 to 200 mg/l). The investigated solutions were prepared 100 ml. The mass ratio of liquid and solid phases was 1:100. The amount of adsorption (mmol/g) was calculated by the formula:

с с 0 ecu A =-- V,

m where C0 and Cequ. – the source metal and the equilibrium concentration in the solution, mmol/l; V – the volume of solution l; m – mass of sorbent of g.

Results and discussion

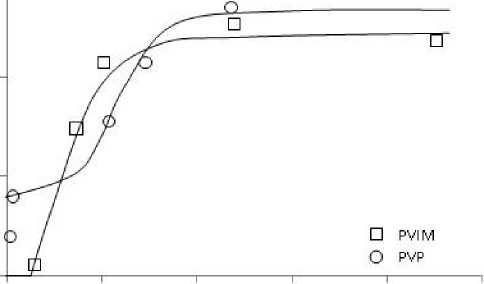
Assessment of the adsorption capacity of modified aluminosilicates in relation to ions of Nickel (II) was carried out on the basis of the analysis of adsorption isotherms. Adsorption equilibrium time corresponding to the constancy of the concentration of nickel (II) in solution was 2 hour. The obtained isotherms are shown in Fig. 1.

As it can be seen from the presented data (Fig. 1), the maximum value of adsorption in the region of low concentrations are aluminosilicates modified with PVP. The average value of adsorption when the modification is increased 3 times and reached 17 mg/g.

It is known that equilibrium in the adsorption system depends on the nature of interaction between adsorbent-adsorbate [11]. Model of adsorption of Langmuir, Freundlich, BET, Dubinin-Radushkevich and others describe these interactions in different ways [12]. So elucidation was the possible applicability of the mentioned models in the interpretation of experimental results.

Thus, the Langmuir isotherm equation has the form

КС

A = A ” 1 + v ecu. ,                                                        (1)

• ¹    + ^K C ecu.

where A – the current value adsorption mmol/g; A ∞ – maximum amount of adsorption, mmol/g; K – constant of adsorption equilibrium; C_ecu. – equilibrium concentration of heavy metal ions, mmol/dm³.

The obtained experimental results were processed using the Langmuir equation, given in linear form:

A

=--1--*---------.

A „   A „ К C ecu.

The results are presented in Fig. 2.

From graphic linear dependency (Fig. 2). The largest segment of the line that intersects with the ordinate axis, the marginal value of adsorption A ∞ , and the slope of the line – adsorption equilibrium constant of the K, the values of which are presented in Table 1.

From the above data (Table 1) shows that the maximum value of the marginal quantities the adsorption characteristic for aluminosilicates modified PVIM. The obtained equations allow to calculate the amount of adsorption of nickel (II) ions modified by adsorbents.

0,3 1

0         0,2        0,4        0,6        0,8         1

C equ, mmol/dm³

Fig. 1. The adsorption isotherms

Table 1. Parameters of the Langmuir model

Modifiers	A А ∞ , mmol/g	A А ∞ , mg/g	К	The linear form of the Langmuir equation	R2
PVIM	0,289	17,023	8,693	1/А = 0,3987·1/С ecu + 3,466	0,689
PVP	0,251	14,820	25,165	1/А = 0,1582·1/С ecu + 3,9811	0,956

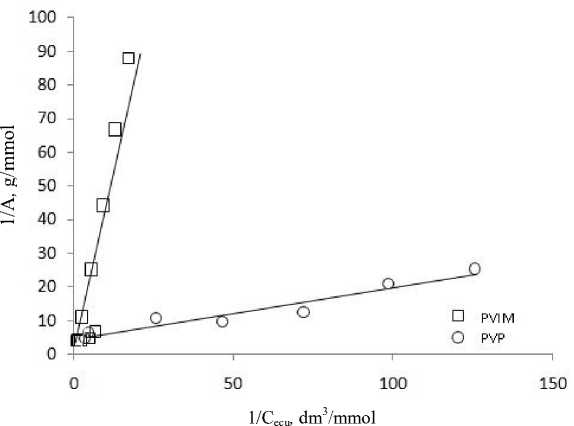
Fig. 2. The adsorption isotherm in coordinates linear form of the Langmuir equation

It is known that in the inhomogeneous medium filling the adsorbent surface are widely used empirical Freundlich equation [12]:

,

A = Kf • C n_u f ecu.

where A – adsorption quantity mmol/g; C ecu . – equilibrium concentration of heavy metal ions, mmol/dm³; K_f and n – constants. Most use the Freundlich equation in logarithmic form:

lgA = lgK f +1/n·lgC ecu.                                                            (4)

To investigated the modified aluminosilicates constructed according to the linear Freundlich equation logarithmic form (Fig. 3) from which the constant Kf and n (Table 2) are defined.

Adsorption centers Freundlich models have different energy values, and above all there is a filling of active adsorption centers with maximum energy. The constants Kf and n enable the comparison of the adsorption capacity of the modified aluminosilicate. When the concentration of the nickel ion (II) in a solution of 1 mol/l of the adsorption of the ions is equal to a constant Kf, and the parameter n indicates the intensity of adsorbent-adsorbate interactions. Thus, the nickel ion adsorption (II) on silica-alumina modified PVIM flows faster in the initial period of time, and in the case of the adsorbent, modified PVP is most intensive interaction adsorbent nickel ion (II).

Table 2. The model parameters Freundlich

Modifiers The linear form of the Freundlich equation Kf n R PVIM lgA = – 0,039 + 1,444·lgCecu. 0,915 0,692 0,945 PVP lgA = – 0,400 + 0,440·lgCecu. 0,398 2,270 0,906 lg A

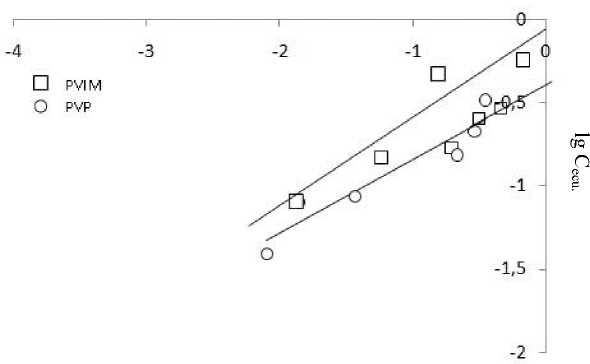
Fig. 3. The adsorption isotherm in coordinates linear form of Freundlich equation

For a description of all types of adsorption isotherms using the BET theory. The equation of the isotherm multilayer adsorption BET:

A „ • c • (C/C 0 )

(1 - C/C 0) • [1 + (c - 1)(C/C о)], where A – adsorption quantity mmol/g; A∞ – limiting monolayer adsorption capacity mmol/g; c – constant for a given adsorption system is directly related to the heat and entropy of adsorption; C, C0 – equilibrium and the initial concentration of heavy metal ions, mmol/dm3.

Adsorption BET equation in a linear form:

C/C 0

A(l - ^C/C о )

A „ • c

c — 1

+-- C/C ₀ .

A» • c to

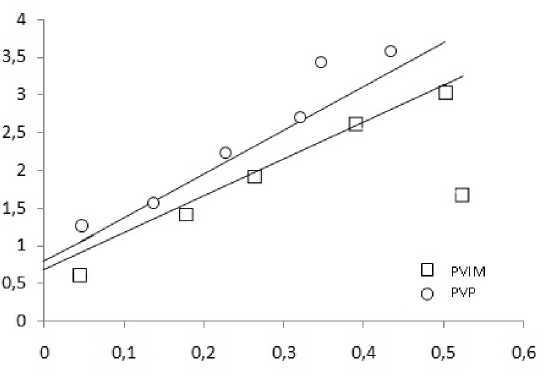
Using the equation of BET adsorption in linear form, built adsorption isotherms for the studied aluminosilicates (Fig. 4).

From linear dependencies shown in Fig. 4, the tangent of the angle of inclination of the straight and the size of the segments, direct intercept with the ordinate axis, determine the limiting adsorption capacity of monolayer A ∞ and c (tabl. 3).

The maximum value of the monolayer adsorption capacity characteristic of aluminosilicates modified with PVP. Due to the fact that the constant c in the equation is a ratio of BET two equilibrium

C/C 0

A(1 - C/C 0

С/С 0

Fig. 4. Adsorption isotherms in coordinates the linear form of the equation BET

Table 3. Parameters BET model

Modifiers The linear form BET equation А∞, mmol/g c·10-3 R PVIM С/С. -------0---= 24,010(C/C0) + 0,678 A(1-C/C • )              °0 0,041 36,413 0,868 PVP A(“oC.) "5,816(C/C•)+ 0789 0,151 8,371 0,846 constants c = k1/k2, it can also be considered the equilibrium constant, i.e. to calculate the standard Gibbs energy there can be used: ∆G °C = – R·T·ln c = – R·T·ln k1/k2.

The equilibrium adsorption process data were processed using a model isotherm Dubinin-Radushkevich

А = Аm·exp(-k· ε2),(7)

where k – constant (mol2/kJ2) associated with the adsorption energy; ε – Polyani potential (kJ/mol) showing the isothermal operation of transfer mole of nickel ion (II) from the equilibrium volume of the solution to the adsorbent surface and defined by the expression.

ε = RTln(1+1/C),(8)

where R – universal gas constant, kJ/mol·K; T – absolute temperature, K.

Dubinin-Radushkevich equation (7) in logarithmic form:

ln A= ln Am – k· ε2.(9)

Using the equation of adsorption Dubinin-Radushkevich in a linear form, are built according to ln A = f (ε2) (Fig. 5).

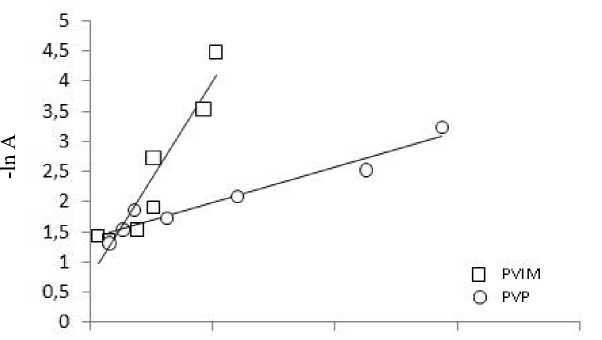
О          50         100        150        200

ɛ2, kJ2/mol2

Fig. 5. Adsorption isotherms in coordinates the linear form of the equation of Dubinin-Radushkevich

Table 4. The parameters of the model Dubinin-Radushkevich

Modifiers	The linear form of equation Dubinin-Radushkevich	А m mmol/g	k, mol 2/kJ2	E, kJ/ mol	R
PVIM	– ln A = – 0,745 + 0,045 ε2	0,475	0,0045	10,54	0,874
PVP	– ln A = – 1,393+ 0,012 ε2	0,248	0,0019	16,22	0,936

The slope of the represented straight segment and the intercept on the ordinate was determined constants k and Am. The model of Dubinin-Radushkevich indicates the nature of adsorption of the adsorbate on the adsorbent and can be used to calculate the free energy of adsorption:

E = (–2k) -0,5 (10)

The results are shown in Table 4.

It is known that if the value of E is between 8 and 16 kJ/mol, the adsorption process takes place by ion exchange mechanism; if the value of E is less than 8 kJ/mol, the adsorption process is physical. In this case, for all modified aluminosilicates value of the free energy of adsorption, ion exchange mechanism at the point, and fixing of nickel ions (II) has the chemical nature of the [13-15].

From the analysis of the correlation coefficient values (Table 1-4) represented the Langmuir model, Freundlich, BET, Dubinin-Radushkevicht follows that the adsorption on aluminosilicates modified PVIM best describes the model of Freundlich adsorption on aluminosilicates modified PVP – Langmuir model.

At the modifying PVIM greatest convergence of results is obtained using the Freundlich equation. In the latter case, the modification of aluminosilicates PVP adsorption process best describe the adsorption model of Langmuir and Dubinin-Radushkevich.

Conclusions

• 1.    Process of adsorption of ions of nickel (II) on the modified aluminosilicates is investigated, adsorption isotherms are constructed.

• 2.    The obtained experimental datas are processed with application of models of Lengmyur, Friendlich, BET, Dubinin-Radushkevich. Constants of these equations are defined. It is shown that adsorption on aluminosilicates of the modified PVIM is in the best way described by model of adsorption of Friendlich, on aluminosilicates of the modified PVP – Lengmyur’s model.

• 3.    Dubinin-Radushkevich’s model is used for calculation of the free energy of adsorption. For all modified aluminosilicates, value of the free energy of adsorption, point to the ion-exchange mechanism, and fixing of ions of nickel (II) has the chemical nature.