Деформация обувных материалов на полусфере

Появление нового оборудования для формования верха обуви, работающего по принципу одновременного приложения растягивающих усилий в различных направлениях заготовки верха обуви, обусловило повышение интереса к исследованию механических свойств кожи при ее испытании на двухосное растяжение. Существует несколько вариантов испытания кожи на двухосное растяжение, которые отличаются между собой в основном принципам приложения деформирующих сил. Общим для всех этих испытаний является применение образца кожи в виде круга.

На рисунке 1 показаны схемы основных испытаний на двухосное растяжение.

Рисунок 1 – Схема нагружения материала при двухосном растяжении

• 1    - растяжение с помощью эластичной мембраны;

• 2    - растяжение с помощью металлического шарика;

• 3    - растяжение плоским торцом цилиндрического пуансона;

• 4    - растяжение пуансоном в виде стакана с вмонтированными по краю роликами;

• 5    - растяжение сферическим пуансоном.

Среди указанных методов испытания кожи наиболее часто используется метод продавливания зажатого по кругу образца шариком (см. рис. 1), диаметр которого значительно меньше диаметра образца. Так как сама обувная колодка представляет сложную пространственную форму, то при непосредственном получении ее копии требуется решить большое количество практических проблем, а исследованием характера деформации на шарике получить достаточно точные характеристики самого материала нельзя. Для первоначального анализа механических параметров процессов формования кожи нами была выбрана достаточно простая форма, наиболее приближенная к форме носочной части колодки, – поверхность полушара.

В государственном стандарте Республики Беларусь для определения прочности при продавливании и растяжении продавливанием текстильных материалов, в том числе нетканых (СТБ ИСО 2960-2001), принят для испытаний образец материала диаметром 113 мм (площадь 10000 мм2), применяющийся в ряде стран, использующих метрическую: систему единиц. Данный размер образца позволяет провести более точные измерения растяжения продавливанием. Аналогично и для кожевенных материалов вместо образцов диаметром 30 мм (1,2 дюйма), применявшихся ранее долгое время, есть необходимость перейти к исследованию процессов деформации на образцах диаметром 113 мм.

В усовершенствованном способе испытания кожи на двухосное симметричное растяжение, предложенном А.Ю. Зыбиным [1], в работах М.П. Куприянова [2], А.И. Комиссарова и А.Н. Жарова [3] учитывается толщина исследуемого материала, так как диаметр рабочей части образца невелик (10 или 25 мм), при этом относительное удлинение рассчитывается с использованием угла, определяющего положение первоначальной дуги образца, что усложняет дальнейшее проведение экспериментальной проверки полученных теоретических результатов. На характер деформации образцов большего диаметра ( R = 113 мм ) при продавливании пуансоном в виде жесткой сферы толщина исходного материала существенного влияния не оказывает.

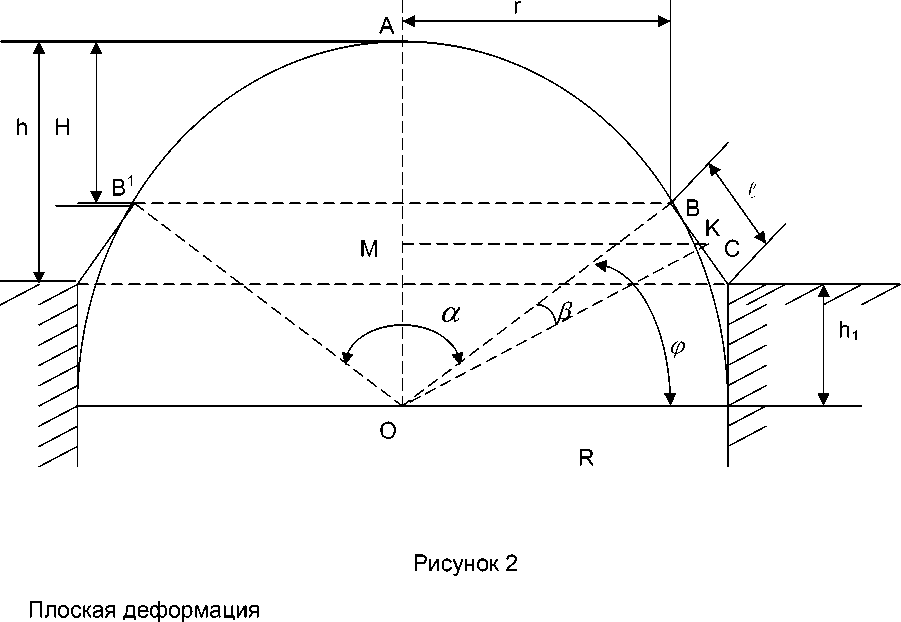
Рассмотрим растяжение образца кожи радиусом R (см. рис.2) шаровым сегментом того же радиуса и получим зависимости плоской деформации и относительных удлинений материала по меридиану и параллели от одной величины h - высоты подъема шарового пуансона.

Ε=SS0 ⋅100 %,                      (1)

^s      S 0

где S ₀ - первоначальная площадь деформируемого кругового образца радиуса R , т.е. S ₀ = π R ² , а S – площадь поверхности, полученная продавливанием исходного образца при подъёме шарового пуансона на высоту h . При этом данная площадь состоит из суммы двух площадей: S ₁ - площади боковой поверхности усечённого конуса с радиусами оснований R , r и образующей l , а также площади S ₂ - части образца, непосредственно контактирующего с поверхностью полушара.

Площадь боковой поверхности усеченного конуса S ₁ = π ( R + r ) ⋅ l , с учетом

π

того, что ∠ OBC = 2 образующая конуса l = h ₁ = R - h , r = R ⋅ cos ϕ , поэтому

S1 = πR(R - h)(1 + cosϕ).

ϕ h

Т.к. tg = 1 2R

,

то 1 + cosϕ =

2R2

R2+(R-h)2

Подставив в формулу (2) в полученный результат (3), имеем

^S 1 ⁼

2πR3(R - h) R2+(R-h)2.

При нахождении площади сферического сегмента с центральным углом контакта материала со сферой а и высотой H = R — R sin 9 . С учётом того, что

2 hR               „     2nR2 h2

sin 9 = — ---- , эта площадь S_? = —;--------- - а значит, полная площадь

R2 + h12                  2 R2 + (R — h )2

, о 2nR 3( R — h) + 2nR2 h2 поверхности после продавливания на высоту h S =----R———h^----

.

Тогда полная плоская деформация

Е. =

' 2 R (R — h) + 2 h2 v R2 +(R — h)2

—

1 -100%.

(1) вычисляется по следующей формуле:

Окончательно после преобразований

получаем

Е. =

h2

R ² + ( R — h )²

-100%

Расчёт меридиального относительного удлинения формуемого на полушаре материала определим по формуле

L-d

Е m = —-100%, d где d - первоначальный диаметр образца, L – длина образца по меридиану после подъёма пуансона на высоту h. При этом L = aR + 2(R — h), и если учесть, что то

( а 2

V

п

— 97

= п — 4 arctg

R—h

R

L = nR — 4R arctg 1 —

h )

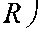
+ 2( R — h ) . Тогда формула (5) принимает

следующий вид:

Е

— 2 arctg 1 — V

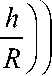
- 100%

При расчёте радиального (по параллели) относительного удлинения материала учтём, что некоторый первоначальный радиус образца р после его деформации

U шаром приобретет новую величину р' = AB + BK. Так как при этом происходит и

некоторое меридиальное удлинение,

. =р

m

р

1 , а

значит, первоначальный

AB + BK радиус был равен р =--------

ОС

R-2 + Rtge

.

С учетом полученных

m

m

п

результатов (6) и (7) имеем р = R -

2 arctg 1

+ tgP

. Относительное

п

2 arctg 1

h+1 R

удлинение образца по выбранной параллели найдем по формуле

2nKM - 2пр

E =---------—•100% или E = rr

2пр

KM -11-100%.

V р )