Деформационные и кинематические параметры вальцевой формовки

Одним из современных способов производства труб большого диаметра является вальцевая формовка [1].

В технологических линиях с применением вальцевой формовки для получения трубной заготовки под сварку лист вначале изгибают в трехвалковых вальцах до заданного радиуса, затем выполняют догибку плоских участков в клети догибки кромок, после чего выполняется сборка трубы и наложение технологического шва [2, 3].

В процессе вальцевой формовки основным настроечным параметром, определяющим радиус заготовки на выходе из очага деформации, является глубина погружения верхнего валка [4].

Одним из основных преимуществ вальцевой формовки перед другими способами является более равномерное распределение деформаций по периметру сечения трубы, полу- чаемое благодаря непрерывности процесса гибки. Тем не менее участки поперечного сечения трубной заготовки, примыкающие к недеформированным прямолинейным участкам, имеют радиус, отличающийся от радиуса готовой трубы.

С целью получения равномерного распределения деформаций в поперечном сечении заготовки в начале прохода погружение верхнего валка целесообразно производить одновременно с вращением валков [5].

Глубина погружения верхнего валка должна удовлетворять двум условиям:

• –    создать необходимый резерв мощности для пластического изгиба листа;

• –    обеспечить необходимый радиус трубной заготовки.

Для определения параметров процесса, удовлетворяющим этим условиям, воспользуемся расчетной схемой, представленной на рис. 1.

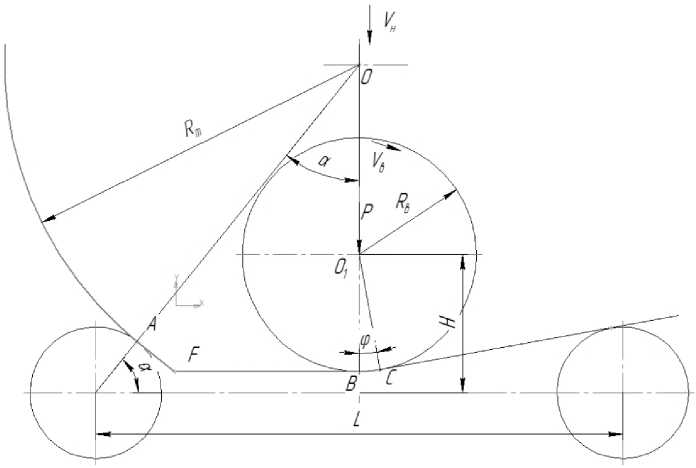
Рис. 1. Расчетная схема формовки

При построении расчетной схемы приняты следующие допущения.

• 1.    Центр окружности трубной заготовки радиусом R_m лежит на вертикальной оси симметрии (точка O ).

• 2.    Неизвестная заранее кривизна листа на участке АВ между точками контакта с верхним и нижним валком линеаризуется и представляется ломаной линией АРВ. Точка перегиба F является точкой пересечения касательной к поверхности нижнего левого валка в точке А и касательной к поверхности верхнего валка в точке В.

• 3.    Прогиб листа под действием сил тяжести на участке между точками касания с верхним и нижним правым валком отсутствует.

В качестве теоретической базы для методики расчета параметров процесса целесообразно использовать энергостатический метод [6], который успешно применяется для анализа процессов производства бесшовных труб [7].

Рассмотрим методику определения глубины погружения Н, обеспечивающую получение заготовки с заданным радиусом R_m.

Запишем уравнение баланса мощности процесса с учетом сделанных допущений.

• 1.    Мощность в рассматриваемую систему подводится за счет перемещения верхнего валка в вертикальном направлении со скоростью V_u. Эта мощность равна

• 2.    Мощность в рассматриваемую систему подводится за счет вращения верхнего валка с угловой скоростью ш. Эта мощность равна

• 3.    Мощность в рассматриваемой системе затрачивается на изгиб листа в точке F на угол а. При этом меняется направление вектора скорости при неизменном его уровне (рис. 2).

N_p = PV_u , (1) где Р - сила, действующая на валок при его погружении.

N_M = Мш, (2) где М - момент, подводимый к верхнему валку.

С учетом того, что действие равно противодействию, подводимый к валу момент равен моменту сопротивления вращению, создаваемому силами трения Т на дуге ВС . Следовательно,

М = Т • RB. (3)

Примем, что силы трения подчиняются закону Амонтона – Кулона [8, 9] и равнодействующая вертикальной нагрузки приложена в середине дуги ВС. Тогда

M = Rb^Pcos ^ , (4) где ц - коэффициент трения; величина угла ф заранее не известна.

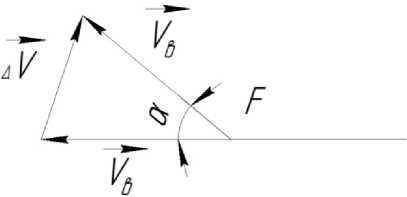
Рис. 2. Схема изменения вектора скорости

Как видно из рис. 2 , в п роцес с е изгиба п рои с ходи т п ов орот вектора с корос ти У_в со скоростью АУ. Не трудн о з а ме ти ть, что с ко-

рость поворота будет равна

АУ = 2ysin - . ^в 2

В свою очередь, L

2(R _m +R H ) , где R_H- радиус нижнего валка.

Значит,

АУ =

V b L

^2(R m ^+R H )

Пов орот в е к тор а ск оро с ти п рои с хо д и т под действием сил.

Поск оль к у и зм енени е углов вызывается ка с а т е льн ыми н а п ряж е ни ями и в ра с с ма три в ае мом слу ча е и мее т ме сто п ла с ти че ск и й из г иб, к а са те льные н а пряже н и я должны б ы ть р а в ны соп рот и в лен ию м е та л ла п лас ти че ск ой деформации сдвига T_s [ 10] . Э то н а п ря же н ие де й с тв у е т н а п лощ а д и , р а в н ой п рои зв е д е н и ю толщины листа ( h ) н а ег о ш и ри н у . Ес ли д ля у доб с тв а п ри н ять ш и ри н у ли с та ра в н ой е д и н и ц е , то мощ ност ь , з ат рачив а ема я на и зги б, будет равна

N_n = |^Ts ^

V _B L

^(R m ^+R H )

С у че том сд е л а н н ых в ыкла д о к у ра в н е н и е ба ла н са мощ нос ти за п и ше тс я в в и д е

РУ + р — • R_B • Р • cos - = - T_sh ^н R_B ^в            2    2 ^s

V b L

^{( R} m ^+R H )

отсюда усилие , д е й с тв у ю щ ее н а в е рхн и й в алок, равно

Р =

TshL

(R m +RjD^+HtoS ^ )

Пол ученн ы е у ра в нен ия соде р жа т д в е неизвестных величины: Р - у с и л и е , де й с тв ующее на верхний валок, и ф - угол, опреде л яю щ и й дли н у д у ги к он та к та лис та с в е р хн и м валком.

Следует отметить, что только с помощью геометрических построений величину угла ф определить нельзя, так как длина дуги контакта, величину которой он определяет, должна обеспечить достаточный резерв сил трения для продвижения и изгиба листа на участке АВ. Следовательно, для решения задачи необходимо привлечь еще одно уравнение физического характера.

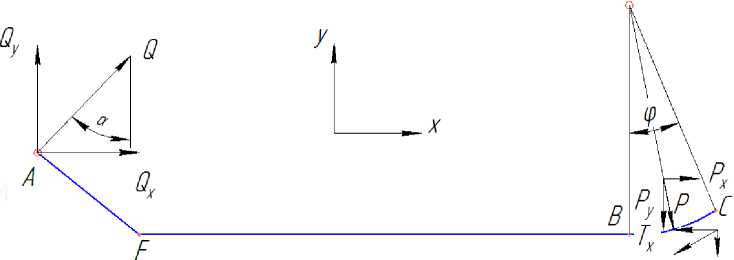
4. Рассмотрим условия равновесия сил участка листа AC.

Расчетная схема представлена на рис. 3.

В этом случае условие равновесия проекций сил на ось ох примет вид

или

Qsina + Psm^-— Tcos 2 = 0,        (12)

где Q — реакция нажимного валка; Т — сила трения, действующая на контакте с верхним валком.

Если принять за основу закон трения Амонтона – Кулона, получим

Qsma + Psin--Рц cos2=0.(13)

Условие равновесия проекций сил на ось оу примет вид

Qy — Ру — Ту = 0,(14)

или

Qcosa + Pcos2-Pц sin- = 0.(15)

5. Запишем основную систему уравнений: г Р =_______TshL

(R m +R н )(у ; +нс°5 * )'

" Qsina + Psin- - Рц cos- = 0;

^ Qcosa + Pcos 2 - Рц sin ^- = 0.

Записанная система из четырех уравнений содержит четыре неизвестные величины: Р, Q i , Q₂, ф. Следовательно, поскольку число

/- г,

Рис. 3. Расчетная схема

у ра в н е н и й ра в н о коли че с тв у н е и звес тн ых, теоре ти че ск и он а мож е т бы ть реш е н а .

Введем обозначение sin 77 = z. Тогда

cos 2 = V1 — z2.

С у че том э того п е рв ое уравн ени е с и с т е мы за п и ш етс я с л е д у ю щ и м о бра зом:

P =----- E^----- л 7)

(Яж+адО^^).          ( v в

Из в торого у ра в н е н и я с и с те мы и ме е м :

z = ± ^{ц ctg} “ ¹ . (24) V^(^+ctga)+ctg ² a+l

6. Подставим выражение (24) в формулу (17). В результате получим зависимость для определения усилия погружения верхнего валка

P =

T _s hL

Qsina = ^PV1 — z2 — Pz; „ = P(^V1-z 2 -z) sina . Подс та в и м э тот р е з у л ьта т в	(18) (19) п осле д не е
уравнение системы:
P ^ — PV1 — z2 — ^Pz = 0; sina	(20)
P ^(^1— z 2 — z ) — sina
—PV1 — z2 — ^Pz = 0;	(21)
P[(^V1 — z2 — z)ctga —
—V1 — z2 — ^zj = 0.	(22)
Поск оль к у п ри п ла с т и че с к ом и згиб е

P Ф 0, справедливо

(^V1 — z2 — z)ctga —

—V1 — z2 — ^z = 0.                (23)

Р еш ая ур авнени е о т н о си т ел ьно па р аме т-

^2(й т ⁺ Я н )1 ун ⁺ Ц I ¹    u+ctga 2.J

(H ctga-1) + 1j

T _s hL

2(Я т +Я н )

Vh ,         H(H+ctga) Vb L . . /(^+ctga)2+(^ ctga-1)2

.

С учетом того, что

sina =

имеем

ра z , находим:

L

2(Ят+Ян)

ctga = ^4 р'^'н)   1            (27)

7. Определяем из физических условий величину углаф

ф = 2arcsin-T:    ц ctg“ 1      .

V^(^+ctga)+ctg ² a+1

После этого величина внедрения верхнего валка, обеспечивающая формирование цилиндрической обечайки радиусом R_m, может быть найдена с помощью простых геометрических соотношений.

С этой целью воспользуемся расчётной схемой, представленной на рис. 4.

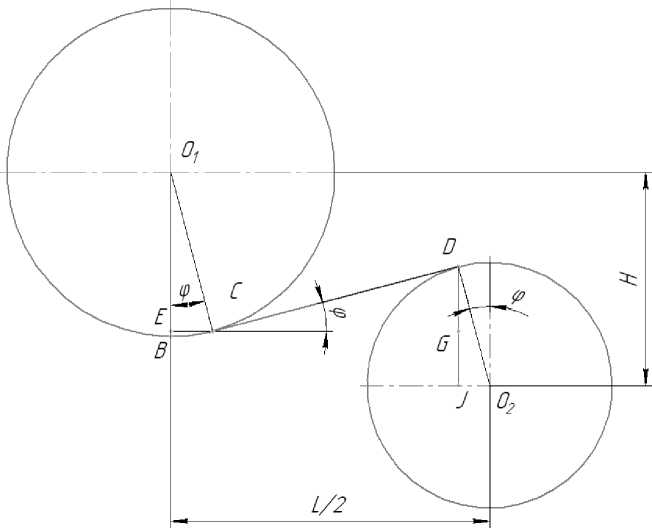
Рис. 4. Расчетная схема глубины погружения верхнего валка

4000 3 RHH
ээии 1 °- 3000
X X СО Э^ПЛ -
О 2ьии о ЭЛЛЛ
■ ZUUU о "О" -1 г
ф 1500 X х 1000
> 500
Л
300          500          1000         2000         3000

Радиус заготовки Rm, мм

Рис. 5. Изменение усилия формовки в зависимости от радиуса заготовки