Деформирование тонкой пленки после утери контакта с цилиндрическим основанием с учетом влияния его кривизны, податливости и действия поперечных сил; отслоение, расположенное в окружном направлении

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2024PNRPU MECHANICS BULLETIN

Покрытия являются важным элементом в различных приборах и устройств в микро- и наноэлектронике, с помощью которых повышается твердость и износостойкость эксплуатируемых приборов. В процессе эксплуатации деталей, особенно в сложных термомеханических условиях, в покрытиях могут развиваться дефекты. Одним из характерных видов дефекта является отслоение покрытия [1–7].

Механические напряжения, возникающие в покрытиях во время эксплуатации деталей, оказывают существенное влияние на их долговечность и надежность. В частности, сжимающие напряжения могут способствовать краевому отслоению и скалыванию покрытий [8; 9] либо приводить к их короблению или гофрированию [10-12].

Также на процесс отслоения покрытия влияют такие факторы, как кривизна и податливость основания, влияние которых исследовалось для металлических, оксидных и полупроводниковых покрытий в [12; 13]. В работах [14; 15] исследовалось влияние кривизны, а в [16–18] – податливости основания на параметры возможного отслоения покрытия. Одновременное влияние кривизны и податливости основания исследовалось в работах [1; 19; 20]. В частности, в [19] рассматривалась модель, не учитывающая влияние поперечных сил на компоненты смещения и угол поворота в точке заделки, в [20] – модель слабо искривленной пластины. В работе [1] исследовалось отслоение покрытия в осевом направлении в рамках более общей теории нелинейных цилиндрических оболочек, в данном исследовании анализируется отслоение покрытия в окружном направлении.

В работе получены выражения для скорости высвобождения энергии при отслоении вдоль границ отслоения, угла поворота в точке заделки, также получен профиль отслоившегося участка покрытия. Исследованы зависимости скорости высвобождения энергии, угла поворота в точке заделки от значений податливости основания и ее кривизны , также рассмотрено условие существования критической ширины отслоения аналогично исследованиям [1; 19; 20].

1. Постановка задачи, общие соотношения

Рассмотрим деформирование отслоившегося участка покрытия толщины h , соединенного с цилиндрическим основанием радиуса R . Для решения данной задачи воспользуемся криволинейной системой координат (рис. 1), компоненты смещений в срединной поверхности покрытия обозначим: v ( а, в ) , и ( а, в ) , w ( а, в ) ■

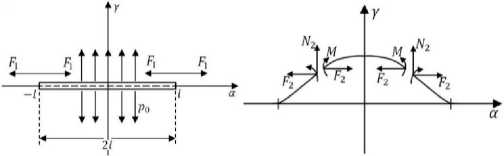
До отслоения на покрытие вдоль координатных линий α, β, γ (рис. 2) действовали сжимающие усилия

F = g h ,

P 1 = g h ,    g >  0,

N 1 = 0,

где l – полуширина отслоившего участка покрытия. На основание действовало растягивающее напряжение

h

P o = g— .

0 _R

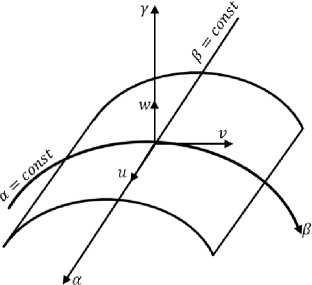
Рис . 1. Криволинейная система координат

Fig. 1. Curvilinear coordinate system

b

a

Рис . 2. Распределение силовых параметров : а – до отслоения покрытия ; b – после отслоения покрытия

Fig. 2. Distribution of force parameters: a – before delamination of the coating; b – after delamination of the coating

После отслоения на покрытие вдоль координатных линий α , β , γ ( рис . 3) действуют усилия F ₂, P ₂, N ₂ и из гибающий момент M в точке заделки .

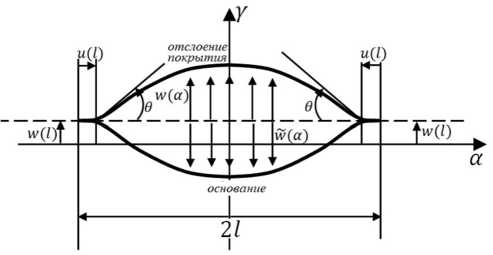
Рис . 3. Геометрия отслоения покрытия

Fig.3. Delamination of the coating

Для достаточно протяженного отслоения сечения , расположенные вдали от концов , могут быть рассмот рены в приближении плоской деформации , при этом одна из тангенциальных компонент смещений отсут ствует, т.е. v ( а, в ) = 0 , а остальные компоненты зависят только от одной переменной: u = u ( a ) , w = w ( a ) . В дальнейшем анализе используются следующие параметры (см. рис. 3):

0 = - w '(a )| = l - угол поворота отслоения в точке заделки;

w ( a ) - смещение поверхности основания.

Дифференциальные уравнения изгибаемой по образующей цилиндрического покрытия имеют вид [21–24]:

d ⁴ w     д ² w v          о h

D ад+F да -RF +(v- 1)R+Eh

Eh ³

12 (1 - v2)’ dF = 0, dα

где D – изгибная жесткость покрытия, E и ν – модуль Юнга и коэффициент Пуассона покрытия.

Граничные условия записываются в виде dw(a = 0 ) = 0’ dw(a = 0) = 0’ dα dwM

^(a = l ) =     ,    w ⁽ _a = l ) = w i .

dα2

Неизвестными в рассматриваемой задаче являются изгибающий момент M , смещение в точке заделки w_l и усилия F ₂ , N ₂ .

Из условий баланса сил, а также закона Гука следует, что компоненты F ₂, P ₂, N ₂ имеют вид [19; 20] (для удобства обозначим F 2 = T , T >  0)

F 2 = T ,

P ₂ = v F ₂- ( v-1 ) о h - ( 1 - v² ) Eh I w l,        (5)

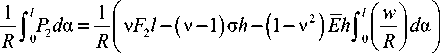
Граничные условия примем в виде условий обобщенной упругой заделки [1, 25].

E

^ u ( l )

- hw '( l )

। ^{w (} l ) ,

fa ^a 11

a

I ^a 13

a 12	a 13'	" F		E
a 22	a 23	h - 1 M	’ E =7	E . (6) 1 - v2 ) ( )
a 23	a 33 |	I N >	(

Эффективные продольные F и поперечные (перерезывающие) N усилия определяются следующим образом

N = N ₂

F = F 2 - F 1 = T - o h ,

αα

— N 1 = R - ^ v F 2 1 + ( 1 — v ) о hl — ( 1 — v ²

)Eh\' I - I d a I — 0 =

'   ^{J 0}1 R J    J

' ee =

F 1 h P 1 h

v Tl + ( 1 — v ) о hl — ( 1 — v² ) Eh J 0 1 R I d a l .    (7)

о =— F 2 =— T

αα _hh ^,

P 2 ^{о вв} = h ’

С учетом выражений (7) граничные условия (6) записываются в виде

Eu ( l ) = a 11 ( T — о h ) + a ₁₂ h M + a ₁₃ N ,

— Ehw' ( l ) = a ₁₂ ( T — о h ) + a ₂₂ hM + a 23 N ,      (8)

Ew ( l ) = a ₁₃ ( T — о h ) + a ₂₃ h - M + a ₃₃ N .

Д о

αα

о — о αα αα

^{Д о} вв

— T + о h =- F h “ ~h~ ’

„ 0 _^— P 2 ^{+ о h} = ^о вв ^о вв =

Выражения для компонент дополнительных деформаций [14; 15] в принятой постановке задачи имеют вид

Решение дифференциального уравнения (2) с учетом условия (3) и граничных условий (4) есть

R w (a) = ( vT — (v — 1) оh)--+ C cos (ba) + C2 cos (b2 a), (9)

Eh где

. du 1 ( dw | 2 Де =— + - —

αα da 21 da J

,

w

^Де вв = n ■

R

Подстановка (16) в выражение для дополнительных деформаций (17) дает

C 1 =

b 1 cos ( b 1 1 )

M

D

До„„               — F

αα

E   ^{Д еaa} +         -h

— T + o h du 1 ( dw

—— = T+d v

Eh    d a 2 ^ da

w

+ v—^

R

b 2 ²

( 1 — ( b 2 / b 1 ) 2 )

I

w ( a = l ) — ( v T — ( v — 1 ) оh ) —+       , ⁽¹⁰⁾

'     ’ ^{y v 1} Eh tf D J

du — F ^ — = — dα Eh

1 ( dw

2 [ da

w

— v—.

R

( 1 — ( b 2 / b 1 ) 2 ) cos ( b 2 1 )

M I (11)

Интегрирование данного выражения от 0 до l дает разность тангенциального смещения в точках l и 0. В силу симметрии u ( a = 0 ) = 0, следовательно:

, , - Fl u ( l ) = ——

Eh

w

\ + v— d a.

I R

b 1	= l 2	1 +1	1 1 — 4 EhD T 2 R 2,	(12)
b 2	= l 2	1 —•	1 4 EhD \    T2 R2 ’	(13)

Подстановка (9) в (19) и интегрирование дает

u ( l ) ' -■■ L

Eh

l ν R

REh

( v T — ( v — 1 ) o h ) —

— ^{( C} ,^v sin ⁽ bl ) + C 2^v sin ^{( b} 2 1 ) + ¹      , b — sin b ^{2 1} b ², b — sin ,

{      b 1 R              b ₂ R        8 ^{1 1 ( 1         ( 1} " 8 ^{2 2 ( 2         ( 2} ) )

параметр λ есть

*= :,                 <»>

( b 1 1 ) ( b ₂ 1 ) C 1 C ₂ ( b ₂ lcos ( b ₂ 1 ) sin ( b 1 1 ) — b 1 lcos ( b 1 1 ) sin ( b ₂ 1 ) )

l ³ ( b 1 ² — b 22 )                                _J

Введем безразмерные величины:

Из (9) следует, что прогиб в центре отслоения покрытия равен w (a = 0) = ( vT — (v — 1)o h) Eh + Cl + C2-     (15)

Для определения параметров M , T , w_l в (9) воспользуемся граничными условиями (6).

До отслоения на покрытие действовали напряжения σ0αα и σβ0β , а после отслоения – σαα , σββ :

f = F		N n = T’ σ h
	σ h
	M	σ
m =	σ h 2	е = —. E

После чего с учетом (7) имеем

T = ( f + 1 ) о h ,

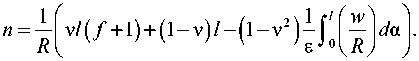
Из условия положительности параметров σ, T , а также того, что с h >  T, следует, что -1 <  f <  0 . Параметр λ в безразмерных величинах примет вид

^Х = l Л = l ^^ = l f ^ = Пп f ) , (23) DEh h

dw ( l )      F     M     N	_ a 12 f e + a 22 m е + a 23 n e, (29)
d a       Eh    Eh 2      Eh
w ( l )     F     M     N _ an + an     + a^ h 13 Eh 23 Eh 2    33 Eh	_ a j3 fe + a 23 m e + a 33 n e. (30)

где η – отношение полуширины отслоения к критической полуширине, соответствующей потере устойчивости отслоения от прямолинейной границы при условии граничных условий типа жесткой заделки:

Вычислим производную от смещения w(a), которая определяется выражением (9)

dw _ - C j b j sin ( b 1 a ) - C 2 b ₂ sin ( b ₂a ) ,

П = l,(24)

l ₀

l0 =    '    7 = hT-.(25)

12 (j - v2) ИЛ2£

в безразмерных величинах принимающая вид

dw ( a   l ) d α

^k J ( bl ) sn ( bll

В безразмерных величинах выражения (9), (20) запишутся следующим образом

1 12е ( C ₂ nn k h

( b ₂ 1 ) sin ( b ₂ 1 ) .

(l)                  £ п h “(vf+j)(1 -v2)kJib

+ ( —] cos ( bl) + ( —] cos ( b ₂ l ) , ⁽²⁶⁾ k h J k h J

Подстановка полученных выражений для u (α), w (α), w ′(α) (26), (27), (32) в граничные условия (28)–(30) дает систему из трех уравнений, определяющую значения трех неизвестных переменных m , f , w_l .

u ( l ) h

f ηεπ   ηπ νε

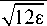
122г ( 1 - v² )

( ^{v f + j} ) ^-

(C1 / h) vsin (b11) nk   (C2/ h) vsin (b21) nk b1l                         b2l

- 8 ( ^b' i ) k C i J ( ^{2 b}' i

- sin (2bl))-1 (b21)fC-] (2b21 - sin (2b21))      - nn 8 k h                    nn

- V12Z ( bl WK C L/M C ^( cos () sin ( b ) - b cos ( b ) sin (  )) , ⁽ 27)

«n           1 2 ( b j - b ₂ 2 )

где

C 1 h

-----2--------- 1 - m n² n² ( b j l ) cos ( b j l ) k

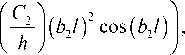
C ₂ _            1              w ( l ) ( v f + 1 ) ле + m n²п²

h ^- ( 1 - ( b ₂ / b ) 2 ) cos ( b ₂ l ) k h     ( 1 - v² ) k 712^    ( b1 ) 2 ^

⁽ b l ^)_ зк 7

1 - АЫ k 2 л² ( f + 1 ) ² e

^{( b} 2 ' ^)_ ^

?   « 2 ( f + 1)7 •

к _ К

R

Также с учетом (21) граничные условия (8) представим в более удобном виде

u ( ^l ) F , M , N                  ™

—— ^{_ a}11       a 12 "ТТГ ⁺ a 13     = a 11^{f 3 +} a 12 m ^{6 +} a 13 n ^e, ⁽28)

hEhEh ² Eh

2. Вычисление скорости высвобождения энергии при распространении отслоения вдоль криволинейной и прямолинейной границы отслоения

Аналогично [1], скорость высвобождения энергии при распространении отслоения в направлении криволинейной границы G_ss вычисляется как высвобождающаяся упругая энергия единицы длины отслоившегося участка, деленная на его ширину, равную 2 l , состоящая из энергии, высвободившейся из изгибаемого участка покрытия A U j , неотслоившегося участка покрытия A U ₂ и энергии, высвободившейся из основания A U ₃.

Первая из данных величин вычисляется как разница упругой энергии отслоившегося участка до и после отслоения

A U j _ U j before - U j after •                  (33)

Удельная потенциальная энергия деформации U ₁ (энергия на единицу объема) есть [15]

K=-a e =-(o e +am£nn+ a £ + an£n+on£n +o £ Ц34)

1    ₂ ij ij ₂αα αα ββ ββ γγ γγ αβ αβ βγ βγ γα γα ^.

В данной задаче последнее выражение упростится до вида

U j ^_ 2 ( ° aa ^£ aa ^{+ C} ₽₽ ^S ₽₽ ) •               ⁽³⁵⁾

Удельная потенциальная энергия деформации до и после отслоения выражается через дополнительные компоненты напряжения и деформации в виде

° aa = ° ⁰a ^{+ A} ° aa    ^£aa = ^£0a ^{+ A £}aa ,

° вв = ° вв ^{+ A} ° ee    ^£вв = ^£вв ^{+ А £}вв ,

F1 = -Lh = -E (A + V£°p ) h = °h

^U 1 before

00  00

aa^£aa ⁺ ° вв^£вв ) ’

^U 1 after = 2 ( ⁽ ° aa ^{+ A} ° aa )( ^£aa ^{+ A £}aa ^{)+ (} ° вв ^{+ А} ° вв )( ^£вв ^{+ А £}вв ) ) ’

Учитывая связь между компонентами напряжений и деформаций, получаем

= -Шг° +V8’k“ +E(e0„+ve°

1 before ₂ αα ββ αα ββ αα ββ ^,

^U 1 after = 2 ( ^E ( ^£L ^{+ V£0} e ) к ^{+ E} ( ^{A £} aa ^{+ v A £} ee ) ^£0 a ^{+ E} ( ^£0 > ^{+ V£} °e ) ^{A £}« ^{+ (3 7) + E} ( ^{A £}aa ^{+ v A £} ) ^{A £} aa ^{+ E} ( ^£ вв ⁺ A- ) A ^{+ E} ( ^{A £} PP ^{+ V A£}™ ) ^£ °P ^{+ + E} ( ^{£ 0} p ^{+ V£}°a ) ^{A e} ₽₽ ^{+ E} ( ^{A £} PP ^{+ v A £} aa ) ^{A £} ₽₽ ) •

Выражение для высвободившейся удельной потенциальной энергии деформации принимает вид

Д U,=iL_f -U.               +&Л +

1       1 before       1 after        ₂            ββ αα ββ

⁺ 2 ^Ar . . ( ^£°a ^{+ v£}°₽ ) ⁺ ( ^{A £}aa ^{+ v A £}₽₽ ) ^{A £}aa ⁺ ( ^{A £}₽₽ ^{+ v A £}aa ) ^{A £}₽₽ ) • ⁽³⁸⁾

Потенциальная упругая энергия, отнесенная на единицу длины координаты β, вычисляется через интегрирование удельной энергии lh/2             lh/2

^{A U} 1 = ^U 1 before — ^U 1 after = J _ _t J _ „ U 1 before^d Y d ^{a -} J — i J — h U - _afier d Y d ^a =

= 1" 1" A Ud у d a = f f    ¹ E (2A £™(ve ° + £°„) +

J - J - h /2      ¹           J - l J - h /2 2    1 ^ee '             PP /

^{+ 2 A £}aa ( ^£0a ⁺ v^ P ) ⁺ ( ^{A S}aa ^{+ V A S}₽₽ ) ^AP - ⁺ ( ^{A S}_₽P ^{+ V A S}«« ) ^{A S}_PP ) ^d Y ^d ^ ^{(3 9)}

Связь между дополнительными деформациями и компонентами смещений имеет вид [14; 22]

P1 = -°°Ph = -E ( Ар + V£°a ) h = °h

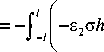
F

Eh

(-T + ° h)

Eh

= £₁ + V£ 2

,             . h³ - 2   1 - 2   1     2 к

- £,° h + v£,£, Eh +-- EK .2 +— Eh £ 2 + — Eh £ 2 d a =

^{1         12}      24 ¹ 2     ¹ 2     ² I

( ° h ) 2     T ² 1   f l (           ,w  ( w                      el ( d ² w (41)

= —=—l -—+ f I 2° h ( 1 - v ) 1 | (1 - v² EEh I d a - d[ —— \ d aA '

Eh     Eh  ^J° (    ³ ’R   \ r R к     'J ^J° ( d a ² )

Энергию A U ₂ определим как работу сил, действующих на неотслоившиеся участки покрытия

A U2 =( T + сh)(- u (a = l))-M (-w'(a = l ))-

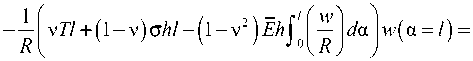
= ( f + 2 ) o h ( - u ( a = l ) ) - m O h ² ( - w '( a = l ) ) - n a hw ( a = l ) • (42)

Энергия A U 3 , учитывающая влияние основания на покрытие до отслоения, записывается в виде [1; 26; 27]

A U3 =

B E ) (< 1 2

EE_s   2 R ²

Удельная упругая энергия не отслоившегося покрытия имеет следующий вид

G = ( ^{1 v} ) ° ² h = ° ² h ° = 2    ET ” 2E

.

Скорость высвобождения энергии (отнесенная к энергии покрытия до потери устойчивости), с учетом выражения (9), а также величин (8), входящих в (42), есть

^{A £} aa = ^£ 1 ⁺ Y K 1 ,

^{A £} pp = ^£ 2 ⁺ Y K 2 •

G^ =(A U1 +A U2 +A Uз)

G 0           2 lG 0

£1 =--+— dα2

du 1

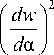
k = d 2 w d α ²

ε

w

R,

K 2 =

_d 2 _w d β ²

(1 -(f +1)=) + 2 (1 - v) kkH πε

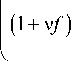
επ

( 1 - v² ) k л/12е

3 k ²

Подставляя последнее соотношение в (39) с использованием выражения (16), получаем

^{A U} 1 = - 2 ^E J - l J -2 2 ( 2 ^£ 2 ( La ^{+ £0} e ) ^{+ 2} ( ^£ 1 ⁺ Y ^K 1 ) ( ^£0 a ^{+ V£0} p ) ⁺

( C / h ) sin ( bl ) ( C ₂ / h ) sin ( bl )I , +             +               - 1

bl                 b 2 1       ) ^v

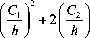
² 8sin ( b ₁ 1 ) ⁺ bl

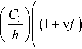
ЕП          ( bl ) ²cos ( b ₂ 1 ) ( C ₂ 1

( 1 - v² ) k Vik ⁺ l (b-   b- ) {h ^J

4 ( 1 + vf ) 2

επ2

—:---5—1

12 ( 1-v² ) k 2

+ ((£j + yKj) + v£2 )(£j + yKj) + (£ 2 + v (£j + yKj)) £ 2) dyda =

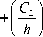
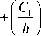
sin ( 2 b ₁ 1 )    8sin ( b₂1 )

bl bl

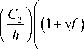
επ

( 1 - v ² ) k kA

( b ₂ 1 ) 2 cos ( b ₁ 1 ) 1 ²( b 2² - b 1² )

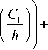
sinA b A ¹ - A ⁽ 2 ( b 1 l ) 4 ( C J ² + 2 ( b 2 1 ) 4 ( C ² J + ( b 1 l ) ³ ( C Ln ( 2 b 1 l ) + b 2 1 ^J П п I v h )           I h ) v h )

⁺ ( ^b 2¹ ) ³ [ C T I sin ( ^{2 b} 2¹ ) ⁺ -рЕЕЕЕ ( C ¹ [ C T I cos ( ^b 2 ^l ) sin ( b ^{1 1} ) ⁺ L ^h J                ^{l ( b} i ^b 2 ) L ^h JL ^h J

8 ( b 1 1 ) ² ( b 2 1 ) ³ 1 C Y C 1                     ( ^{E +} E s )_;2 FT

,2z,2 ,2, I T II     I cos (^l) sin (b2l) I + ----k П^3s - l (b2 - b1 ) L h JL h J                  J     Es

12ε

πη

( ( f + 2 )( « 11 f + a 12 m + « 13 n ) + m ( « 12 f + a 22 m + a 23 n ) +

+ n ( a ₁₃ f + a ₂₃ m + a ₃₃ n ) ) .

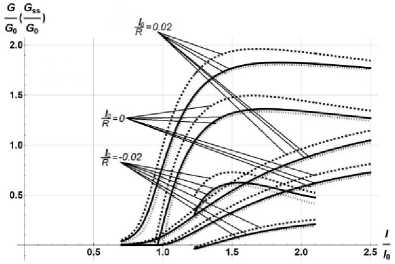
Рис. 4. Зависимость скорости высвобождения распространении отслоения вдоль криволинейной

Аналогично тому, как это делалось в [1], скорость высвобождения энергии при распространении отслоения вдоль прямолинейной границы G рассчитывается как непосредственное изменение упругой энергии при увеличении длины отслоения [18–20]

энергии при (монотонные

ветви) и прямолинейной границы (ветви с максимумами) от

Y при Yf = 0,01 и при I0/p = 0, +0,02,-0,02; жесткое l0         E                  R

G _d [ A U 1 +A U 2 +A U ₃

G ₀ db

2 G 0

основание - сплошные линии; EE = 1 - пунктирные линии; условие жесткой заделки – точечные линии

Fig. 4. Dependence of the rate of energy release during the propagation of delamination along a curvilinear (monotonic branch) and rectilinear boundary (branch with maxima) on ^l _l when

G где ss определяется с помощью (46).

G ₀

Значения коэффициентов матрицы жесткости a ij , ( i , j = 1,2,3 ) есть [1; 16; 17; 20; 28-32]:

Ye = 0.01 and 1Yr = 0, +0.02,-0.02; the rigid base is shown with solid lines, E/- = 1 is shown with dashed lines; the condition Es of a rigid clamping is shown with the dotted lines

a ₁₁

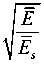
a ₁₂

2 ³

hE ,(47)

^bEs J

a₂₂ = 128, a ₁₃ = 1 + V38, a ₂₃ = 2 + 68 ² ,

( к 1^/3

8 = 0,635 =   ,

L E s J

1 I E a₂₂ =

³³ 6n L E s

^s

83π

+ Y + 327

+ In

6 E^ 1li-} E J h

, (49)

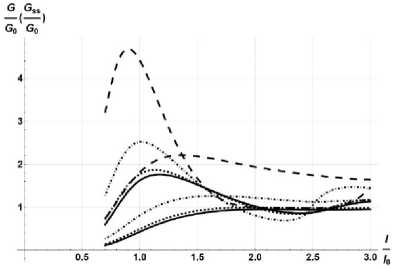
Рис. 5. Зависимость скорости высвобождения энергии при распространении отслоения вдоль криволинейной (монотонные ветви) и прямолинейной границы (ветви с максимумами) от ^l l ₀

где Y = 0,5772... - постоянная Эйлера.

3.    Результаты численных расчетов

Графики зависимости скорости высвобождения энергии при распространении отслоения вдоль криволи- нейной и прямолинейной границы поворота θ в точке заделки от параметра

I , угла

/ G0 J l для раз-l0

личных значений относительной податливости основа ния E , а также для различных величин кривизны ос-Es нования представлены на рис. 4–7. На рис. 8, 9 представлены профили отслоения покрытия при разных значениях l . Все расчеты были выполнены для значе-l0

ния коэффициента Пуассона, равном v = 0,3.

при = 0,01 и при Y = + 0,1; жесткое основание ER

сплошные линии; EE = 1 - пунктирные линии с короткими штрихами; E/- = 10 - штрихпунктирные линии, Е/= = 100 - s

s

пунктирные линии с длинными штрихами

Fig. 5. Dependence of the rate of energy release during the propagation of delamination along a curvilinear (monotonic branch) and rectilinear boundary (branch with maxima) on ^l when l ₀

Y: = 0.01 and when 0/„ = + 0.1; the rigid base is shown with ER solid lines; E/- = 1 is shown with dotted lines with short strokes; Es

ЕЕ = 10 is shown with dash-dotted lines, ^E/- = 100 is shown

s

s with dotted lines with long strokes

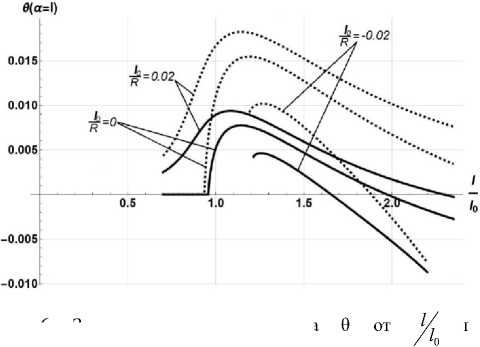
Рис. 6. Зависимость угла поворота

Fig. 6. Dependence

при

= 0, + 0,02, - 0,02; жесткое основание - сплошные линии;

= 1 - пунктирные линии the rigid base is shown with solid lines;

= 0, + 0.02, - 0.02;

E/— = 1 is shown with dotted lines

E

Es of the rotation angle 0 on  l/ when l0

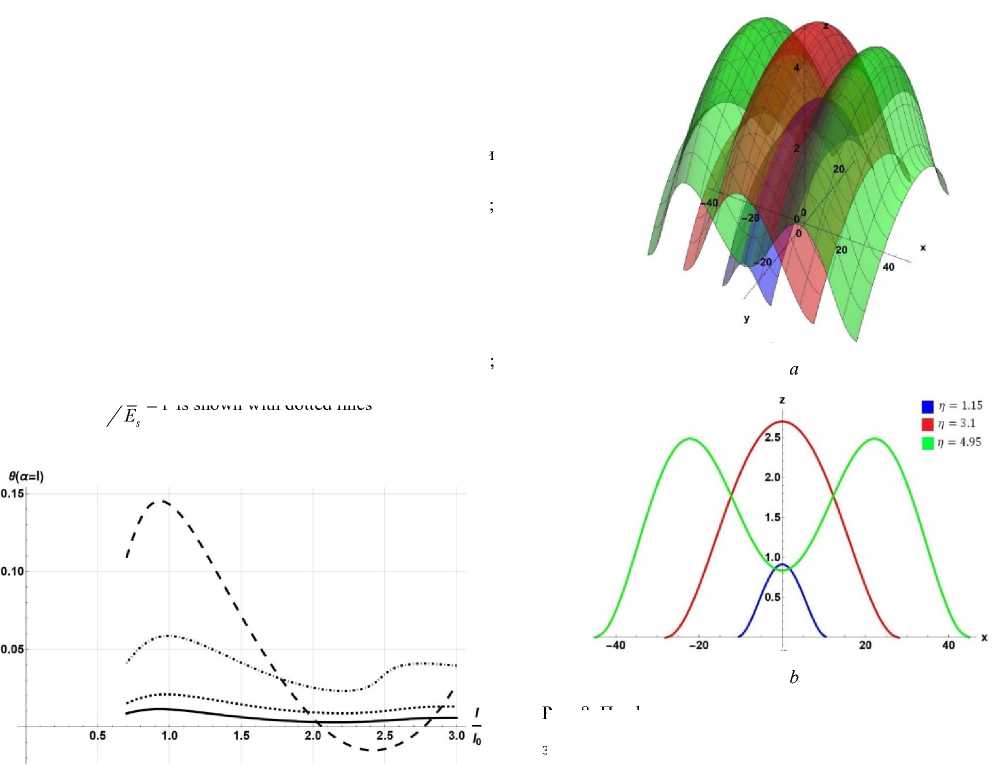
Рис. 8. Профиль отслоения покрытия в зависимости от разных значений n = l/ при l0/„ = + 0,05, E/^ = 1: а - в трехмерном l0        R             Es пространстве; b – в проекции на двумерное пространство

Рис. 7. Зависимость угла поворота 0 от ^ при ^ =+ 0,1;

жесткое основание - сплошные линии; E/— = 1 - пунктирные ли-Es нии с короткими штрихами; E/— = 10 - штрихпунктирные Es линии; E^ = 100 - пунктирные линии с длинными штрихами Es

• Fig. 7.    Dependence of the rotation angle θ on

  = + 0.1;

  
  

the rigid base is shown with solid lines; E/- = 1 is shown with dotted Es lines with short strokes; E/- = 10 is shown with dash-dotted lines; Es

E/- = 100 is shown with dotted lines with long strokes Es в максимуме первого. Можно заметить (рис. 5), что для достаточно податливых оснований существует некоторая критическая ширина отслоения, для которой отслоению становится энергетически выгоднее развиваться за счет удлинения, чем за счет расширения, и чем податливее основание, тем меньше критическая ширина.

• Fig. 8.    Profile of coating delamination depending on different values

  of П =

  
  

l/ when l0/г> = + 0.05, E/= = 1: a - in three-dimensional l0         R             Es space; b – in projection onto two-dimensional space

По результатам вычислений можно сделать вывод, что при положительной кривизне основания отслоение покрытия возникает при напряжениях ниже уровня потери устойчивости (скорости высвобождения энергии положительны для всего диапазона l   (см. рис. 4, 5), угол поворота l0

в точке заделки также положителен (см. рис. 6, 7), а наличие податливости основания только усиливает этот процесс.

Также замечено, что начиная с определенного отри- цательного значения кривизны, а именно 0/r < -0,02,

Как показано в [1], зависимости скорости высвобождения энергии (47), соответствующие росту отслоения в осевом и окружном направлениях, должны пересекаться отслоения покрытия не происходит ввиду того, что в этом случае данный процесс энергетически невыгоден. Расхождение между результатами, полученными с уче- том влияния поперечных сил и перемещений (ai3 ^ 0), и упрощенными моделями (ai3 = 0) становится замет-

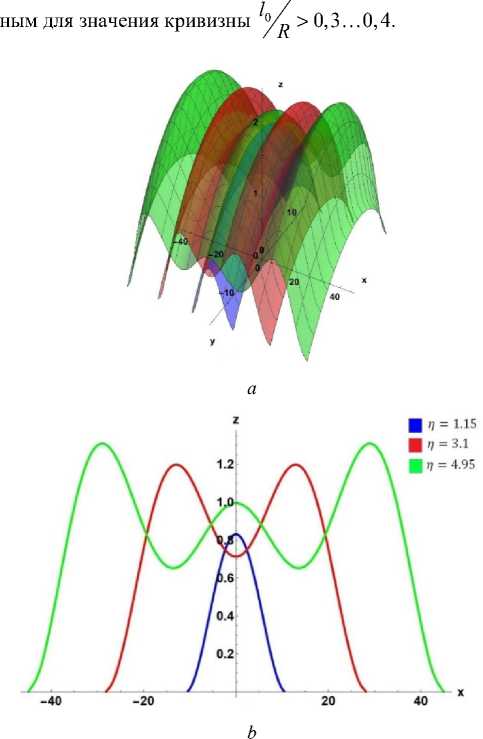
Рис. 9. Профиль отслоения покрытия в зависимости от разных значений n = lX при l0/р =+0,1, E/^ = 1: а - в трехмерном l0        R           Es пространстве; b – в проекции на двумерное пространство

• Fig. 9.    Coating delamination profile depending on different values

of П = l/ when l0/ = +0.1 E/^ = 1: a - in three-dimensional l0         R           Es space; b – in projection onto two-dimensional space

Обратим внимание и на то, что при увеличении кривизны в результатах профиля отслоения покрытия (см. рис. 8, 9), скорости высвобождения энергии (см. рис. 5) наблюдается эффект «волнистости» (гофрирования), чего не наблюдается для задачи, рассмотренной в работе [1], причем, чем больше значение кривизны, тем сильнее проявляется данный эффект. Аналогично, в рассматриваемой задаче из зависимостей для угла поворота в точке заделки (см. рис. 6, 7) наблюдается критическая ширина