Деградация статических свойств и долговечность структурно-неоднородного материала

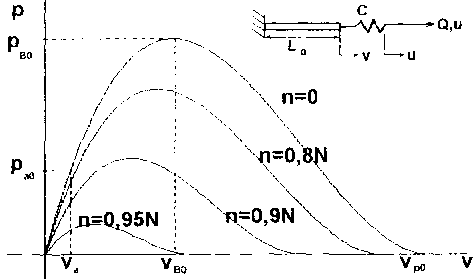
Рис 2. Циклические диаграммы вырождения упругих, прочностных и деформационных свойсгв образца при циклировании

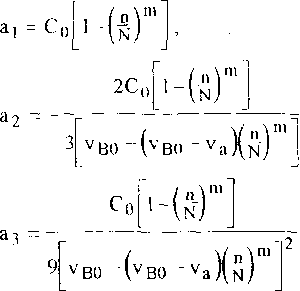
Заметим, что для расчета требуется так называемая машинная диаграмма P_n(v) Вопрос о пересчете ее в зависимости о(е) здесь не рассматривается Согласно принятой модели вырождения статических свойств (8) следует P_BN -0,что отвечает «чисто» усталостному, без статического долома, разрушению образца. Совокупность долговечностей N = N(v_a) при различных значениях амплитуды v_a образует множество точек B_v диаграммы Велера. Для ее аппроксимации примем часто используемое выражение

N-v^=A, (10) где у и А - константы материала

Циклирование с заданной амплитудой деформации va = const

Поведение тренированного образца из промышленного композита в составе механической системы вновь исследуется методом теории катастроф Согласно изложенной выше методике по формулам (9) и (8) строится циклическая диаграмма Pn (v) при фиксированном числе циклов П]. Затем в выражении (4) для полной энергии ГЦ полагаем Ф(у) = -Pn (v). Полученная в результате вычислений поверхность Ми отвечает более сложной катастрофе сборки. Поверхности равновесных состояний Ми и Mq в случае п = 0 строились при следующих числовых значениях параметров системы: Ьу=2мм, dy = 2мм, Су =15700

Н

мм

4 Н           Н

Е0=1(Г--у, С = 3140—.

мм2          мм

Поверхность содержит катастрофу сборки с координаты которой точкой возврата (начала сборки),

Су vK-2vB0> СК~ЦЦ>

8 vB0

к 3

При С<СК имеет место катастрофический скачок с верхнего листа поверхности на нижний, если же С > С^ - деформирование равновесное

Циклическая тренировка меняет поверхности Ми и Мд. При квазистатическом деформировании тренированного образца заданным перемещением точка возврата смещается в область меньших жесткостей. Опасный (со скачком) при заданной жесткости путь нагружения после циклирования становится безопасным Кроме того, снижаются критические параметры vzj и mz1, отвечающие катастрофическому скачку а 2     II а2 | а1 +

За3               За3

/ 2 а3 / з uzi7c + lJvzi + /C'vz.l + /C'vzl

С учетом (9) для vzl имеем

У/П-2у_в - v_B^4 з[|ьс(с₀ГЦ^^ j

При нагружении тренированного образца заданной силой lai/        а?/ 2  а3/ з „             \ vz2 - vB>uz2 /C+1Jvz.2 + /Cvz2 + /с ' vz2> Qz ~ C(uz2 " vz2) O2) и разрушение всегда (независимо от С) динамическое при максимальном значении функции Pn(v).

Заметим, что при n = N точка возврата на поверхности смещается в область бесконечно больших податливостей Q^ ~> 00), поскольку

Ски’ЧНк) ]/3 = °

Усталостное разрушение при циклировании с va = const действительно равновесное, без долома. Число циклов до разрушения при va = const определяется кривой Велера (Ю).

Циклирование с заданной амплитудой силы Qa = const или перемещения подвижного захвата машины ua = const

Для построения кривых Велера Bq и Ви при стационарном циклировании с постоянными амплитудами Qa или иа требуется ввести то или иное правило суммирования повреждений. Такая необходимость продиктована тем, что при неизменных значениях параметров цикла Qa или иа амплитуда перемещений va возрастает вследствие деградации свойств материала образца.

В качестве кинетических кривых вырождения несущей или деформационной способности материала будем использовать зависимости (8). В случае силового подхода, например, два состояния материала, достигнутые при разной истории циклирования, эквивалентны, если одинакова остаточная несущая способность,

PBl(vabnl) = РВ2 (va2in2)

Согласно второму из соотношений (8), при Ш = const, из последнего равенства определяется эквивалентное число циклов

N 2

ПЭкв. =п2 =П1                                      (13)

совпадающее с прогнозом по линейной гипотезе суммирования. N[ и N2 - точки кривой Bv, отвечающие амплитудам перемещений va[ и va2, соответственно. Если же m * const и меняется при переходе с одной амплитуды на другую, то т1

( П) ™2

n3KB.-N2        .                                 (14)

Алгоритм расчета долговечности образца при нестационарном (по деформациям) нагружении основан на замене реального процесса кусочностационарным. В течение малого числа циклов Ап полагается va = const и строится циклическая диаграмма Pn(An,v) Затем из условия Qa = const или ua = const находится новое значение амплитуды va (разное для двух случаев циклирования), при котором проводится следующее догружение на Ап циклов.Интенсивность вырождения свойств материала на новой ступени циклирования определяется условием (13) при m = const или (14) при переменном m = m(va). В экспериментах наблюдалось изменение показателя m в пределах 2.6.

В частном случае, когда m = const, использование условия (13) приводит к следующим выражениям для коэффициентов циклической диаграммы на К-й ступени циклирования а1К ~СК>

2а 1к а2К - ~

3vBK а IK о 2   ’

9vBK где

А К Аш

Ск=С₀ 1- Е4г

К

А™

^VBK = ^vB0 ' (^vB0 ” ^vaK) Z^n"

Максимум по циклической диаграмме для выражением

К -й ступени определяется

рвк - Рво

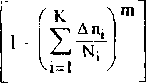
В расчетах сохранено условие vPK = 3vB^ .

Меняя в первом из выражений (8) коэффициенты aj,a₂ и аз на а^,а₂к ^и азк соответственно, получим искомое выражение для циклической диаграммы после К ступеней циклирования по Ап циклов. Остается провести статический расчет по приведенной выше методике и найти значения критических параметров v_z1^,v_z2k_, ^uz1k ^и QzK Если окажется, что какой-либо из указанных параметров при циклировании на следующей ступени А п окажется больше его критического значения на предыдущей ступени, то расчет прекращается. Долговечность образца N _q (или N _u) определяется числом циклов при (А' - 1) ступени догружения

К-1

Nq = XAnf

1=1

Очевидно, что чем меньше Ап, тем точнее расчет, а в пределе , при Ал) осуществляется поцикловое суммирование повреждений.

Учитывая результаты (12) квазистатического нагружения заданной силой и выражение (15), заметим, что циклирование с заданной амплитудой Qa = const неизбежно заканчивается статическим доломом образца при выполнении условия

Qz2 = ^РВК = Qa, имеющего смысл критерия усталостного разрушения.

В случае нагружения заданной амплитудой ua = const условие разрушения образца следующее:

• ^а)    ^vaK-^vz(K-l)>^рВК^>0, 1

• ^б)    Р_ВК=О,       ^vaK^{z(K-l)                    ^^}

Случаи а) и Ь) в условии (16) отвечают усталостному разрушению образца со статическим доломом и “чисто” усталостному (равновесному) разделению его на две части, соответственно.

Числовой пример расчета долговечности образца

Данные числового примера с построением поверхностей катастроф при квазистатическом нагружении дополним следующими: у =2, /1=320, что при амплитуде ¥^=0,2 мм дает, согласно (10), долговечность N = 8103. В примере рассматривались амплитуды va < 0,2мм, что отвечает области многоцикловой усталости.

Результаты числового примера с построением кривых Bv, Bq, Bu приведены на рис.З. Снижение модуля упругости при циклировании, заложенное в модели вырождения свойств (8), приводит к значительному (в примере - порядка 50%) расхождению кривых Велера. Если показатель m = const в формулах (8) не зависит от параметров цикла, то суммирование повреждений линейное и долговечность образца также не зависит от числового значения m.

При линейной зависимости m = b - 100va / 3, кривая Велера занимает промежуточное между кривыми Bq и Bv положение В примере с модельным образцом, где интенсивность накопления повреждений не зависела от уровня амплитудного нагружения цикла, предсказывалась зависимость долговечности от вида граничных условий. В рассматриваемом примере, где это ограничение снято, использована модель вырождения свойств (8), также наблюдается существенное влияние способа стационарного циклирования на долговечность образца.

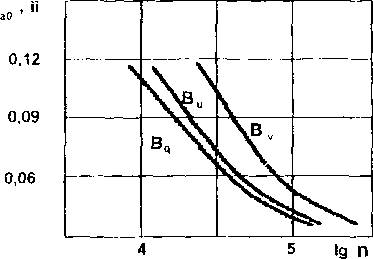
Рис.3.Кривые усталости при различных граничных условиях стационарного циклирования

Авторы выражают признательность профессору Стружанову В.В. за ряд ценных замечаний, сделанных при обсуждении работы.