Действие подвижной нагрузки на ребристую цилиндрическую оболочку с упругим заполнителем

DOI:

Собственные колебания и распространение свободных волн в цилиндрических оболочках, взаимодействующих с жидкостью, исследовались многими авторами, в частности в работах [1, 2, 3]. При этом рассматривались осесимметричные и не осесимметричные задачи, применялись различные модели для жидкости и оболочки. Вопрос о действии подвижной волны давления на цилиндрическую оболочку, заполненную или окруженную жидкостью, менее изучен, причем было рассмотрено только осесимметричное нагружение [4, 5].

В данном работе с помощью интегрального преобразования по осевой координате и рядов Фурье по углу получено решение задачи о движении вдоль бесконечно длинной цилиндрической оболочки, взаимодействующей с идеальной сжимаемой жидкостью нормального давления, произвольного по длине и окружности, но неизменного во времени профиля [6, 7]. Скорость движения нагрузки постоянна, и в статье она рассматривается для случая, когда она меньше скорости звука в жидкости [8,9].

Жидкость заполняет полость между оболочкой радиуса а и соосной с ней жесткой цилиндрической стенкой радиуса b . В статье с использованием полученных результатов в работе [10], найдено решение задачи о действии подвижных нагрузок на бесконечно длинную цилиндрическую оболочку, подкрепленную по наружной поверхности продольными ребрами жесткости и содержащую внутри упругий инерционный заполнитель.

МАТЕРИАЛЫ И МЕТОДЫ

Предполагается, что движущаяся нагрузка передается на оболочку только через ребра, вне ребер нагружение отсутствует. Учитывается дискретность расположения ребер путем записи для них уравнений движения балок с последующим удовлетворением условий сопряжения. Показано влияние числа и жесткости ребер на характер распределения перемещений оболочки и контактного давления на границе заполнителя.

Движение оболочки описывается классическими уравнениями, основанными на гипотезе Кирхгофа-Лява, для заполнителя используются динамические уравнения теории упругости [11]. Движение ребер жесткости подчиняется уравнениям теории балок d4Vi.3

E8kIk~^4 + РЗк?к~^Т = pSk(x,t) - q0k(x,t),(1)

УЛUL где qok давление со стороны оболочки на погонную единицу длины к -го ребра; р§к -интенсивность нормальной нагрузки на k-ю балку; l – число ребер жесткости.

Граничные условия для заполнителя при скользящем контакте с оболочкой имеют вид г = аагх = агв = 0; arr = —qc; иг = ш.                          (2)

Внутренняя поверхности заполнителя принимается свободной от напряжений, тогда г = аа_гх = о_гв = a_rr = 0 .                           (3)

Принимая, что контакт между ребрами и оболочкой происходит по прямым линиям (осям балок), запишем следующие условия сопряжения.

• а)    Внешняя нагрузка на оболочку равна сумме давлений, передаваемых через каждое ребро:

Р (х, 0, t) = 2 ^=1 q₀ k (x,t)8(0 — 0 k ) ;                       (4)

• б)    В местах контакта (0 — 0 k ) перемещения оболочки равны прогибам балок, причем, поскольку положительными считаются перемещения, направленные в сторону выпуклости оболочки, то эти условия имеют вид

ш(х, 0 k , t) = —y k (x, ^)(k = 1,...,l).                         (5)

Для постоянной скорости движения нагрузок и установившегося процесса решение задачи ищется в подвижной системе координат. Применяя преобразование Фурье по q и раскладывая все заданные искомые величины в ряды Фурье по 0 вводим по формулам потенциальные функции, удовлетворяющие уравнениям [12]. Тогда при скоростях движения нагрузок, меньших скоростей распространения волн сдвига в заполнителе, коэффициенты Фурье для перемещений запишутся в виде

• и °п (г,%) = i ^ K_n(m i r)A_n + i ^ I_n(m i r)B_n + m 2i K_n(m_s i r)C_n + m 2i I_n(m_s i r)D_n

и ° _вп(г,^) = i^^ n (m i r)A n + i^I n (m i r)B n + m 2 K n (m si r)C n + m 2i I n (m si r)D n —

— [ ⁿ K n (m si r) — m si K n ₊ i (m si r)\E n — [ ⁿ I n (m si r) — m si I n+i (m si r)]S n ;

u ⁰ n (r,O) = [^rK_n(m i r) - m i K_n +i (m i r)]A_n + [^I n (m i r) - m i I_n +i (m i r)]s_n -

-^^ n^si¹'' ) — ^m si ^K n+i ^(m si ^r)] C_n

- ¹ a ^[r ^I n ^(m si ^r'⁾ - ^m si ^I n+i ^(m si ^r)] D_n + + ^K n (m_s i r)E_n + ^ I_n(m si r)S_n;

ml       m f            c². 1             c\ 1

^m i = ~^m si = —^m = ⁽¹- ^) ² ; ^m s = ^(1- 2 )2>-

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Аналогичным образом с помощью формул (1)-(5) находится гармоника трансформант напряжений в заполнителе. Удовлетворяя преобразованным граничным условиям (2) и (3), выразим функции A_n(O).. .S_n(O) через коэффициенты Фурье радиального перемещения оболочки:

ы°     ‘.■      „‘,

^{A n . ..^S n ) = _detn \\ _aij \\ ^{A n . .. ^Sn)

При этом функции An'(a). ..Sn'(O) вычисляются по формулам detn\a[j У и находятся по формулам элементов asj этих формул, положив t3 = 0. А элементы a6j вычисляются по формулам a6i = ns3 - mO; a62 = n + mOs6; a63 = ns9 - msO; a64 = -n- msOsi2; a65 = n; a66 = n.

Подставляем найденные функции в формулу (6) для ОуГП, а затем полученное выражение рассматриваем при условии ^Гг.п = -qC.n (r = а~) . Тогда находим связь между реакцией заполнителя и рациональными перемещениями оболочки в виде fi(n,O,c)

g(n,f,c)  _ detnWatjW;

a i (n,O, c) = {[(1 +m² s ⁾² + 2n(n - 1)]s₃ + 2mO)A₆ i +

+^{[(1 + m ²^² + 2n(n - 1)^]s₆ + 2mO)A₆₂ +

+2mSO2{[1 + n^]s9+A7}A63-m^O2

• -2m^\1 + n^\s12+A-]Au-s         m2O2m

• -2n[(n - 1)s9 - msO]A6S + 2n[(n - 1)si2 - msO]A66 .(7)

Здесь A6j алгебраические дополнения элементов определителей detn\a[j\. В случае сплошного заполнителя функция fi(n, О, с) вычисляется по формуле (7). Подставляя (6) в преобразованные уравнения движения оболочки, получаем систему алгебраических уравнений относительно u°i,v0,M0 , из которой искомые величины выражаются через коэффициент Фурье трансформант внешнего давления на оболочку. В частности, для трансформанты радиального перемещения получаем

“°W=^^ = ₀^cos(ne-),              (8)

2ku        г ($,П,С)

где функция F(%,n,c^ вычисляется по формулам (7). В (8) коэффициенты Фурье трансформант внешнего давления на оболочку являются неизвестными и должны быть определены с помощью условий сопряжения ребер с оболочкой. Для этого, применяя в подвижной системе координат преобразование Фурье к (4), (6), разложим правую часть (5) в ряды Фурье по в , тогда в пространстве изображений будем иметь

P°(S,e) = ~^'=°(^k=1qok(S)aпk)cos(nв).(9)

Здесь а_пк коэффициенты Фурье функции 8(в — в_к). С учетом (8) формула (7) принимает вид

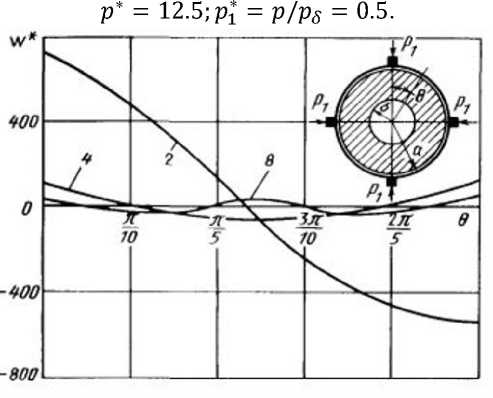
°       1-Е у' fyi     °С2?№

^ (Se)   5kGLn=°\.Lkn=i

Подставляя (10) в преобразованные условия (6), получаем для нахождения q^ систему алгебраических уравнений

эки                               г (^ ,П,С)

Разрешая эту систему относительно q°k, выражаем трансформанты. Для реакции стороны оболочки через прогибы ребер получаем зависимости вида q°k = fk(yl.....у?)(к = 1.....Г) .(12)

Конкретный вид этой зависимости определяется числом ребер и здесь не описывается. Подставляя (12) в преобразованные уравнения движения (5), получаем систему уравнений для определения трансформант прогибов балок

S2 [Г-з^-;^      [РЫЖ.....у;)](к = 1......О,( где ук = ук°/h; cik = 3c2Psk/2/GSk .

Из системы (13) находим трансформанты прогибов балок через нагрузки на каждую из них и жесткостные параметры ребер, оболочки и заполнителя. Формально указанные зависимости можно записать в виде y'k = ^k(Psi,...,Psi)(k = 1,...,l)                          (14)

Подставляя (14) в (12), находим трансформанты давления каждой из балок на оболочку, после чего из (8) определяются прогибы оболочки. Затем с использованием (7) определяются компонент напряженно-деформированного состояния заполнителя. Алгоритм получения окончательного решения существенно упрощается, если принять, что материал и геометрические характеристики ребер одинаковы (Е§к = Eg; р$к = Рз; Ik = 1';^к = F), сами ребра расположены на одинакоюм расстоянии друг от друга, а нагрузки, движущиеся вдоль ребер, имеют одинаковую интенсивность и один и тот же закон распределения по длине. Аналогичные формулы можно записать для определения напряженно-деформированного состояния во внутренних точках заполнителя. Расчеты проведены для следующих значений безразмерных параметров:

к = 0.02; v = v₃ = v_c = 0.3; у1 = 0.1;

Рисунок 1. Изменение прогибов оболочки по окружности для различного числа ребер жесткости.

Figure 1. Change in shell deflection around the circumference for different numbers of stiffening ribs.

На рисунке 1 показано распределение прогибов оболочки по окружности в сечении ^ = 0 для у = 250; а⁴// = 10⁶; a²F/I = 700 в случае двух, четырех и восьми ребер. Суммарная нагрузка и ребра при любом их числе остается постоянной, как и жесткость ребер. Число ребер I, их геометрические характеристики, а также относительная упругость заполнителя варьировались.

ЗАКЛЮЧЕНИЕ

В работе разработана методика расчета и алгоритм для определения перемещения и напряжений оболочки с упругим заполнителем и ребром. Эти процессы позволяют изучить работу оболочки под воздействием различных нагрузок, что имеет важное значение для обеспечения её прочности и долговечности.

Всесторонний анализ условий влияния на жёсткость и устойчивость оболочки создаёт возможность значительно улучшить результаты расчётов. Эти результаты могут быть использованы для дальнейших исследований и разработок в области строительной механики и материаловедения.