Действие вертикальной силы, движущейся по произвольному закону, на бесконечную пластину

Введение . Закономерности динамических процессов в твердых средах, вызванных действием подвижной нагрузки, представляют значительный интерес, а решения подобных задач находят многочисленные приложения и предполагают использование разнообразных методов. В ряде работ для исключения времени из числа независимых переменных вводилась подвижная система координат [1–2] или рассматривалась квазистатическая постановка задачи [3–6]. При решении указанных задач достаточно эффективными оказались метод конечных элементов [7], вариационные [8–10], а также прямые методы [11–13]. В работах [14–15] применялся метод граничных интегральных уравнений, а в работе [16] — метод, основанный на применении фундаментальных решений соответствующих дифференциальных уравнений. В настоящей работе этот метод применяется для решения задачи о действии на бесконечную пластину, лежащую на упругом основании, вертикальной силы, движущейся по незамкнутой кривой произвольной формы.

Постановка задачи. Следуя [17, 18], указанная задача сводится к решению уравнения:

, ,             P

A² U + c-²d 2 U + kU = — , t_D

EH3

где U — прогиб пластины; D = 12(1 2); Е — модуль Юнга; ц — коэффициент Пуассона; H — толщина пластины; с-2 = pH; Р — плотность материала пластины; k = o^ ; ko — коэффициент жесткости упругого основания.

Решение данного уравнения соответствует потоку энергии, направленному от источников возбуждения в бесконечность. Будем полагать:

Р = 6(x-x_o(t))6(y-y_o(t)).

Данная сила перемещается по незамкнутой траектории γ, начало и конец которой уходят в бесконечность.

[ x = x ( t )

Параметрическое задание траектории имеет вид: <      ; ² где t — время. Считается, что сила начинает

[ у = у ⁽ t )

движение в начале траектории, расположенном на достаточном удалении от того места, в котором исследуется ее воздействие на пластину в момент времени t = -^ . Поэтому начальные условия в такой постановке отсутствуют.

Материалы и методы. Рассмотрим фундаментальное решение уравнения (1), которое можно получить из уравнения:

A ² W + с ² d_t ² W + kW = 1 6(x - x₀)6(y - y₀)6(t - t).

Известно, что решение уравнения (1) можно представить в виде:

U(x,y,t) = f2_oH_R 2 W(x,x_o,y,y_o,t-T)P(x_o,y_o,T)dx_ody_odT.

В нашем случае с учетом конкретного вида движущейся силы имеем:

U(x, у, t) = J —^ W (x, x₀ (т), у, y₀ (t), t - T)dT.

Применяя преобразование Фурье по времени к уравнению (2), получим дифференциальное уравнение:

A ² W o - w ² c ² W o + kW o = 1 6(x - x o )6(y - У о )с^1ыт

.

Используя принцип предельного поглощения и преобразование Фурье по переменным x и y , и при <7)²

условии k > — можно получить решение уравнения (3):

Wo (x,xoy,yo,^2") = ^^[^(ai^) -/Co(a2^)], где R =[( x - xo )2 +(y - yo )2 ] ^; x= ^jk - ш2/с2; «i = Xe‘n/4; «2 = Xe-1"/4; Ko (z) — функция Макдональда.

При условии k < — решение уравнения (3) выглядит следующим образом:

Wo(x,xo,y,yo,w2/c2) ^^^[^^^(X^) -^(Х^)], где х = J72" - k; H(’) (z) — функция Ганкеля.

Для обращения преобразования Фурье решение W_o(x, x_o,y,y_o, w ² /c ² ) раскладывается по переменной

• —                                            —ш²/       _ы

• —    в ряд по системе ортогональных функций {е    ^с 2 H_k (~)}, где H_k(z) — полиномы Эрмита.

Учитывая, что функция Wo (x, x0,y,y0,^-) является четной по —, в разложении будут присутствовать только четные слагаемые. Тогда:

W o (x,x o ,y,y o , w ² /с ² ) = Z_k =o W 2k (x,x o ,y,y o )e ^—   ^H k (^), где

1      г^                          _Z2/

W 2fc (x,x o ,y,y o ) = ^-^2^= J — _TC W o (x,x o ,y,y o ,z ² )e    ^/2 H 2 _k(z)dz.

Учитывая соотношение:

^      2

Г е ^{—  /2} c² H 2k ( ^ )c

— ОТ

—

' ^iMt dto = 2с J | (-1) ^k c

—

c ² t ² /

2 H_2k(ct),

получим:

W o (x,x o ,y,y o ,t) = 2cJ | ^^(-1) ^k W 2 _k(x,x o ,y,y o )e ^{C £ /2} H 2 _k⁽ct⁾.

В этом случае решение исходного дифференциального уравнения будет иметь вид:

n у ОТ                ,                                    C2(t—T)2

U(x,y,t) = 2cj-2£_TCZ_k =o (-1) ^k W 2k (x,x o (T),y,y o (T))e        ^/2H 2 _k⁽c(t -т)dT.

Сделав замену переменной интегрирования, получим:

U(x,y,t) = £ J J W o (x,x 0 (t -s²²),y,y 0 (t -s²²), 2 т ² ) ^⁽-^e -^(s^ ) H _{2 1}(s^)H _{2 1}( т ^)dsd т .

к= o -„-„                  c                c           ( 2 k J / 2

Такой вид решения позволяет для вычисления интеграла применить квадратурную формулу Гаусса-Эрмита.

Чтобы улучшить сходимость ряда использовался метод Куммера. Следуя этому методу, необходимо подобрать ряд, сумма которого известна, а разность исходного ряда и ряда подобранного должна представлять быстро сходящийся ряд. В качестве такого ряда можно взять:

Механика

U * (x,y, t) = Z ^=o JX J —” W o (x,x o (t - ^a.y^t - ^sV2/c), q) 2gg^ ^{—(s 2 +T 2 )} H 2k№ где q — некоторая неотрицательная величина.

Проинтегрировав по переменной τ и просуммировав, получим:

U * (x,y,t) = neV2W o (x,x o (t),y,y o (t),q).

Окончательно для решения уравнения (1) получим следующее выражение:

U(x,y,t) = U * (x,y,t) +

TO TO TO

+ ^ I I (Wo(x,xo(t-S^2/C),y,yo(t-S^2/C),2T2)-Wo(x,xo(t-S^2/C),y,yo(t-S^2/C),q))x k=0 —to —to x 2г?2(г^ e-(s2+T^H2k(sV2)H2k(TV^^

(2K) ! 2

Для суммирования ряда применялся способ средних арифметических. При этом полагалось: q = 0.

Определив прогибы пластины, можно по известным формулам вычислить остальные компоненты вектора перемещения и тензора напряжений в любой ее точке. Для анализа перемещения энергии упругих волн в пластине вычислялся вектор плотности потока энергии Умова- Пойнтинга:

E = —(o_xu. + o_xyv)i — (о_х- у й + O y V)j.

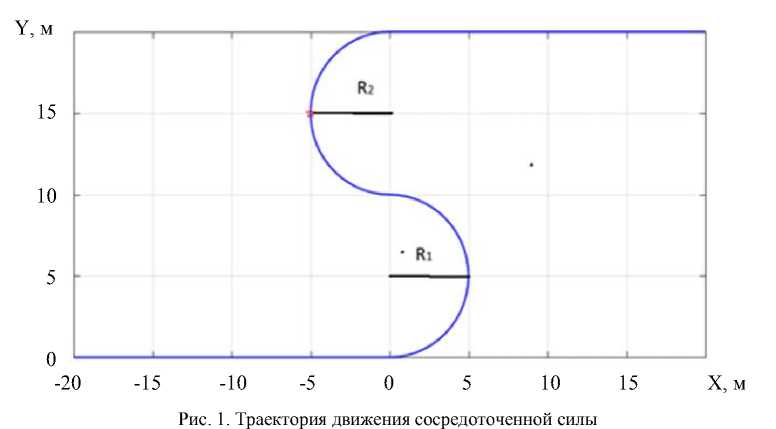
Результаты исследования. Проведены расчеты для случая, когда сила двигается по траектории, состоящей из прямых и дуг окружностей (рис. 1). При этом принимались следующие значения параметров: H = 0,25 м; с = 221 м/c; E = 232469 H/м ^2; µ = 0,36; K = 1,864 м ^-4 . Параметры закона движения силы по траектории подбирались таким образом, чтобы в рассматриваемый момент времени сила всегда находилась в одной и той же точке траектории, отмеченной звездочкой, имея различные значения скорости v и ускорения a , а также при разных значениях радиуса траектории R 2 . Для изучения напряженно-деформированного состояния пластины вычислялись перемещения и напряжения вблизи точки приложения силы.

На рис. 2, 3 представлено изменение перемещений и напряжений при движении сосредоточенной силы по заданной траектории при v = 25 м/c, а = 0 м/c 2 , R 2 = 5 м. Изменение указанных величин вдоль оси Y практически не отличается от их изменения вдоль оси X.

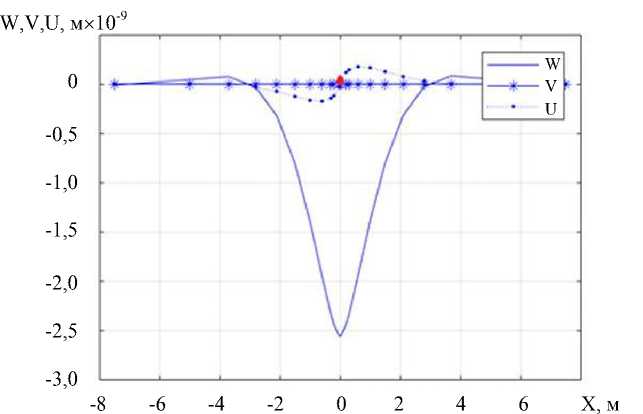
Рис. 2. Изменение перемещений: W — вертикальное; U — вдоль оси X; V — вдоль оси Y

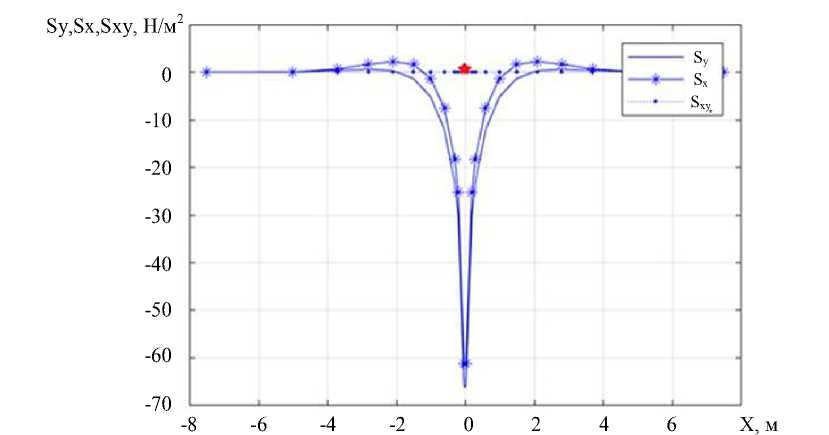
Рис. 3. Изменение напряжений:

W — вертикальное; U — вдоль оси X; V — вдоль оси Y

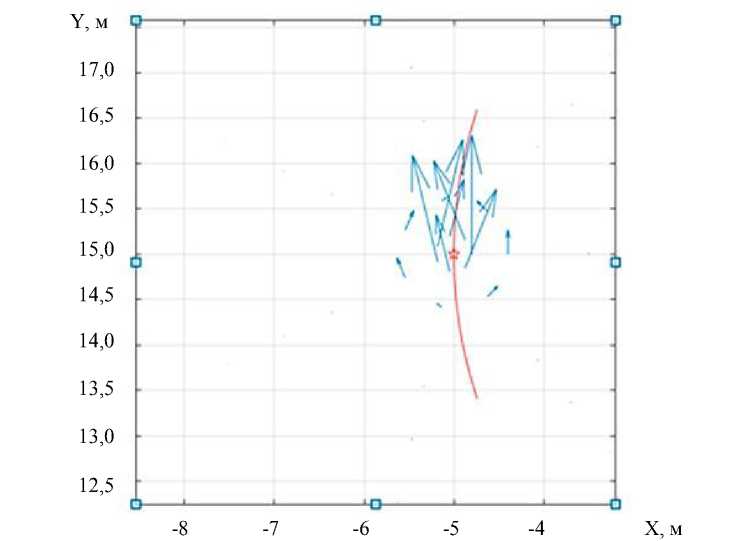
На рис. 4 представлено перемещение энергии упругих волн вблизи сосредоточенной силы, положение которой на траектории обозначено красной точкой. Векторы определяют количество и направление переноса энергии в данной точке.

-7

16,5

16,0

15,5

15,0

14,5

14,0

13,5

13,0

12,5

-8

Y, м

17,0

-4

-5

-чу

-6

■о

X, м

Рис. 4. Вектор плотности потока энергии при v = 25 м/c, а = 0 м/c², R₂ = 5 м

Расчеты показали, что при увеличении скорости движения силы качественного изменения перемещений и напряжений не происходит, а происходит лишь их количественный рост. Незначительное изменение качественного поведения перемещений и напряжений наблюдается только при достаточно больших скоростях, когда выполняется условие v >  c . Это следует из рис. 5, 6 ( а = 0 м/c ² , R₂ = 5 м).

Механика

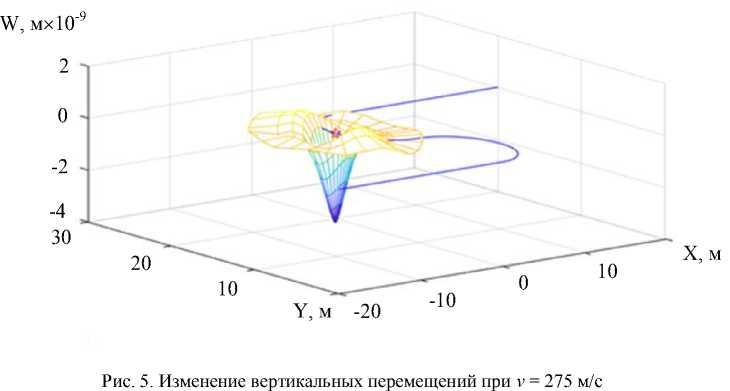
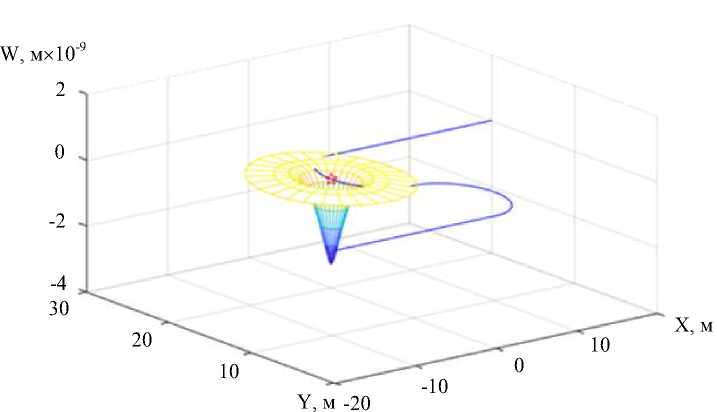
Рис. 6. Изменение вертикальных перемещений при v = 75 м/c

На рис. 7, 8 представлено изменение максимальных вертикальных перемещений W и напряжений S x , S y в зависимости от скорости движения силы при а = 0 м/c 2 , R 2 = 5 м. Остальные компоненты перемещений и напряжений принимали достаточно малые значения и поэтому не представляли конструктивного интереса при анализе напряженно-деформированного состояния пластины.

Вычисления, проведенные при различных значениях ускорения и радиуса R 2 , показали, что эти факторы слабо влияют на напряженно-деформированное состояние пластины. Также слабо зависит от указанных факторов качественная картина распространения энергии волн вблизи сосредоточенной силы.

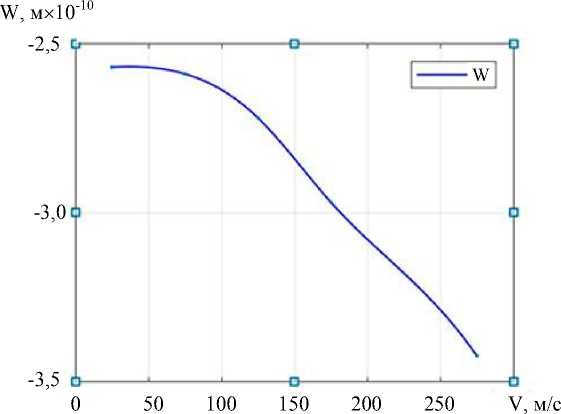
Рис. 7. Зависимость максимальных вертикальных перемещений от скорости движения сосредоточенной силы

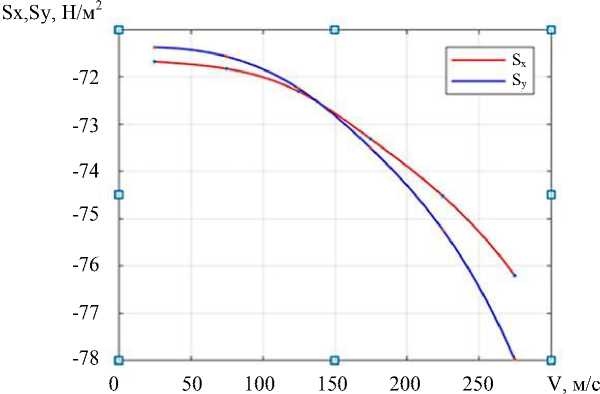
Рис. 8. Зависимость максимальных напряжений от скорости движения сосредоточенной силы

Обсуждение и заключения. Наиболее существенное влияние на напряженно-деформированное состояние пластины и распространение энергии упругих волн вблизи сосредоточенной силы оказывает скорость ее движения. Радиус кривизны траектории и ускорение движения силы влияют несущественно.

Результаты расчета свидетельствуют о том, что метод решения задач о действии подвижной нагрузки достаточно устойчив в широких пределах изменения скорости ее движения. Метод экономичен и прост, т. к. в нем используются уже известные фундаментальные решения.