Действительно ли существуют «лoренцево сокращение длины» движущихся тел и «запаздывание» электрического поля частиц?

Впервые гипотеза о сокращении продольных (измеряемых вдоль направления движения) размеров движущихся тел при неизменности их поперечных размеров была предложена Х. Лоренцем для объяснения «нулевого» результата знаменитых экспериментов А. Майкельсона и Э. Морли по измерению скорости «эфирного ветра» у поверхности Земли. Вскоре А. Эйнштейн показал, что «лоренцево сокращение длины» является одним из следствий специальной теории относительности (СТО). В рамках этой теории был уточнен физический смысл данного эффекта, который заключается в том, что с точки зрения «покоящегося» наблюдателя любое движущееся относительно него тело имеет меньшую длину, чем собственная длина этого тела, измеренная в связанной с ним системе отсчета [1]. Как следствие, согласно СТО, объем V' движущихся тел оказывается меньше объема V этих же, но покоящихся тел, согласно формуле

V' = V J1 - в ²,

где в = |и|/с , и - вектор скорости тела, С - скорость света в вакууме.

Большинство    физиков-теоретиков    считают,    следуя

Эйнштейну, что эффект сокращения длины не вызван какими-то динамическими взаимодействиями, а имеет чисто кинематическую природу: «Становится ли линейка «на самом деле» короче? Прежде всего, ясно, что что никакого сжатия линейки произойти не может. Это следует из основного принципа, положенного в основу специальной теории относительности - принципа равноправия всех инерциальных систем отсчета (ИСО). Во всех ИСО физическое состояние линейки одно и то же. «Укорочение» линейки происходит исключительно в силу различных способов измерения длин в двух системах отсчета. ... Численное значение длины возникает после измерения, а результат измерения зависит от того, приборами какой системы мы пользуемся» [2].

Означает ли это, что эффект сокращения «кажущийся», т.е. «не реален»? Отвечая на этот коварный вопрос, все релятивисты цитируют Эйнштейна: «Вопрос о том, реально лоренцево сокращение или нет, не имеет смысла. Сокращение не является реальным, поскольку оно не существует для наблюдателя, движущегося с телом; однако оно реально, так как оно может быть принципиально доказано физическими средствами для наблюдателя, не движущегося вместе с телом».

Правда, тут же возникает следующий вопрос: будет ли наблюдаться лоренцево сокращение, если часы покоящегося наблюдателя, по показаниям которых определяется скорость движущегося тела, будут синхронизированы не по правилу Эйнштейна?

Эйнштейн был убежден в том, что заметить лоренцево сокращение можно непосредственно, например, визуально наблюдая или фотографируя быстро движущееся тело: «Твердое тело, которое в состоянии покоя имеет форму шара, в движущемся rJ1

состоянии – при наблюдении из покоящейся системы – принимает

— в², r, r»

форму эллипсоида вращения с полуосями

Однако более тщательное исследование (в рамках СТО!) задачи о видимой форме быстро движущихся тел показало, что из-за конечной скорости распространения света и эффекта аберрации визуальное наблюдение или фотографирование этих тел не выявит изменения их размеров, одна эти тела будут казаться нам повернутыми на некоторый угол вокруг оси, перпендикулярной вектору скорости тела [2,67–69]. Этот эффект был качественно подтвержден в опытах с системой световых импульсов, имитирующей гантель и распространяющейся в воде (где скорость света меньше с) [70]. Кроме того, как недавно выяснилось [71], форма тела будет казаться несколько деформированной.

Вопросы «реальности» лоренцева сокращения длины отпадают, если справедлива точка зрения [3–6], согласно которой все релятивистские эффекты, в том числе лоренцево сокращение длины, замедление времени, рост массы и т.д., – динамические , т.е.

являются следствием ускоренного движения тел в процессе их перехода из состояния покоя в состояние равномерного движения.

Одним из теоретических аргументов, который, как считается, подтверждает динамический характер лоренцева сокращения длины тел, является так называемый эффект сжатия в продольном направлении электрического поля быстро движущейся заряженной частицы [7–9]. Этот эффект следует из решения уравнений Максвелла без обращения к постулатам СТО и поэтому считается не зависящим от этой теории. Одним из его математических выражений является формула для вектора напряженности Е электрического поля точечного заряда q, движущегося с постоянной скоростью и [7—9]:

Е5(г, В)

1 qr     1- р ²

л                                      3 ,

^{П£ о}    (1- р ² sin² А)²

где е ₀ - электрическая постоянная, г = |Г| - расстояние от заряда до рассматриваемой точки поля, г — радиус-вектор этой точки, р = |5|/с , в — угол между векторами г и и . Из этой формулы следует, что

«электрическое поле «сплющивается» в направлении движения заряда, причем в тем большей степени, чем ближе скорость заряда υ к скорости с» [2]. «При больших скоростях, близких к скорости света, поле заряда будет все больше сжиматься в плоскости, перпендикулярной направлению движения, и в пределе и ^ с будет иметь вид плоской поперечной волны» [7]. Действительно, отношение расстояний от заряда до точек поля, находящихся на траектории движения заряда (для которых 5 = 0 или 5 = п), Гц, и лежащих в плоскости Σ, перпендикулярной этой траектории и проходящей через заряд (где 5 = п/2), Г^, в которых (точках) модуль значение, равно Гц/г^ = что электрическое поле

напряженности поля имеет одинаковое (1 — в2) / —* 0. Но означает ли это, 4       '    и^С заряда действительно сжимается и, как следствие, происходит реальное (а не «кинематическое») сокращение длин движущихся тел? Ответим на этот вопрос чуть позже.

О чем свидетельствуют эксперименты?

Еще один, значительно более важный вопрос заключается в следующем. Есть ли эксперименты , подтвердившие реальность релятивистского сокращения длины? Оказывается, что их нет.

Действительно, предложенный Эйнштейном метод измерения длины движущихся тел – это всего лишь «мысленный эксперимент», воображаемая процедура, которую в реальности выполнить невозможно.

Опыты Майкельсона и Морли, как оказалось, также нельзя отнести к таким экспериментам. Дело в том, что в последнее время в результате детальных расчетов, учитывающих ряд существенных факторов, от которых зависит вид интерференционной картины, было установлено [10,11], что теория интерферометра Майкельсона, которую использовали сам Майкельсон, Д. Миллер и другие и которая по сей день описывается в учебниках и монографиях, содержит ряд принципиальных ошибок и поэтому не может использоваться для интерпретации опытных данных.

Многие релятивисты все еще считают, что лоренцево сокращение тел подтверждается отсутствием рассеяния пучков заряженных элементарных частиц в ускорителях (см., например, [12]). Такое рассеяние вроде бы должно существовать по причине взаимного отталкивания частиц. Его же отсутствие релятивисты объясняют следующим образом. Относительно наблюдателя, движущегося так же, как и частицы пучка, весь ускоритель движется назад с той же скоростью. Поэтому, согласно общепринятой интерпретации СТО, с точки зрения данного наблюдателя длина ускорителя сокращается, так что время движения частиц в канале ускорителя уменьшается, и пучок просто «не успевает» рассеяться. Так, например, считается, что для пучка электронов с кинетической энергией 10 Гэв длина Стэнфордского ускорителя сокращается с 3 км до 15 см.

Однако очевидно, что в этом рассуждении используется ошибочное предположение о том, между частицами пучка действуют лишь кулоновские силы электростатического отталкивания. В действительности же на каждую из частиц действует еще одна сила – сила электромагнитного притяжения, направленная внутрь пучка [13]. И если пучок движется со скоростью, очень близкой к скорости света, то частицы и на поверхности, и внутри пучка практически не ощущают действия радиальной силы. Такое совместное действие электрических и электромагнитных сил было хорошо известно еще задолго до создания ускорителей и теории относительности.

Наоборот, существует реальный эксперимент, который не выявил лоренцева сокращения длины [14]. В этом эксперименте с помощью специальной оптической установки и пучков лазерного света определялась, в частности, степень деформации диска, вращающегося с очень большой угловой скоростью (более 6000 оборотов в секунду). Согласно СТО, в этом случае длина внешней окружности диска должна казаться неподвижному наблюдателю меньшей, чем 2 n R , где R — радиус диска, не испытывающий лоренцева сжатия, поскольку он в любой точке диска перпендикулярен вектору линейной скорости этой точки. Из-за этого вращающийся диск должен был деформироваться. Однако измерения не обнаружили никакой деформации диска, откуда был сделан вывод об отсутствии реального лоренцева сокращения тел.

По-видимому, впервые сомнения в справедливости вывода специальной теории относительности о сокращении продольных размеров и объема быстро движущихся тел появились в результате теоретического анализа равновесия таких тел, обусловленного необходимостью формулировки релятивистских законов статики. В частности, Х. Арзелье (H. Arzelies) [15] и Ф. Рорлих (F. Rohrlich) [16] еще в середине 60-х годов ХХ в. привели ряд аргументов, основанных на теоретических соображениях и некоторых опытных данных, в пользу идеи о том, что продольные размеры релятивистских объектов вместо привычного лоренцева сокращения возрастают, а эффективный объем релятивистских частиц увеличивается при их движении. При этом, как правило, предполагалось, что поперечные размеры быстро движущихся объектов не изменяются, а их продольные размеры и объем растут с увеличением их скорости υ пропорционально лоренцеву фактору

Y = (1 — в ²) > 1 [15—18]. Для объяснения такого необычного и противоречащего СТО поведения продольной длины был предложен [18] так называемый «асинхронный» метод определения пространственных размеров движущихся объектов, согласно которому эти размеры должны задаваться (в противоположность общепринятой эйнштейновской процедуре измерения) неодновременными положениями элементов, образующих данный объект. В дальнейшем этот подход и его модификации развивались разными авторами (см., например, [19,20]), но они не получили признания, поскольку, с одной стороны, не основывались на конкретной измерительной процедуре, а с другой стороны, их предсказания стали все больше расходиться с новыми опытными данными.

Еще одним важным, но уже экспериментальным, основанием для сомнений в реальности лоренцева сжатия являются результаты ряда опытов по измерению характерных размеров областей взаимодействия элементарных частиц высоких энергий. Такие опыты были целью многих исследований (см., например, [21–25] и др.). Была разработана [21,26] методика оценки этих размеров, аналогичная известному [27] интерферометрическому способу измерения угловых размеров звезд. Данная методика основывается на анализе интерференции пар тождественных бозонов (как правило, пионов), возникших в процессе множественного рождения частиц при ультрарелятивистских протон-антипротонных столкновениях. При этом продольный и поперечный размеры области рождения пионов определяются путем исследования зависимости эффекта интерференции от ориентации пионных пар относительно оси столкновения. В результате проведенных исследований были получены качественные, а в ряде работ и количественные ([23–25] и др.) свидетельства того, что как продольные, так и поперечные размеры области генерации пионов с ростом энергии сталкивающихся частиц возрастают.

Для объяснения полученных на опыте результатов один из авторов исследований [24,25] выдвинул своеобразную концепцию «релятивистской (локационной) длины», изложив ее в обзорной работе [28], и на основе этой концепции предложил так называемую «локационную» формулировку теории относительности [29]. Однако эта концепция была признана ошибочной [30] и отвергнута.

Обзор и анализ результатов всех существующих экспериментов по определению зависимости продольных и поперечных размеров области взаимодействия элементарных частиц от их энергии не входит в задачу автора; эту работу должны выполнять соответствующие специалисты. Остановимся лишь на одном, но весьма показательном факте, относящемся к рассматриваемому здесь вопросу.

Сравнительно недавно, в конце 2008 г., группа ученых из Фермиевской лаборатории в г. Беркли, США, насчитывающая несколько сотен человек, представила результаты анализа своих наблюдений множественного рождения мюонов при столкновениях высокоэнергетических протон-антипротонных пучков в протон-антипротонном коллайдере Тэватрон [31]. Этими учеными было установлено, что при энергии протонов порядка одного ТэВ и выше рождение групп мюонов происходило, вопреки ожиданиям, на значительном расстоянии от оси сталкивающихся пучков – на удалении до 1см и более от оси пучков и даже за пределами вакуумированного канала (радиус которого составлял 1,5 см), то есть, фактически, уже в теле детектора. При этом такие события происходили примерно в 20 % случаев (150 000 из 750 000), а максимальное количество мюонов, рожденных в одном таком событии, достигало восьми, что позволяет говорить о рождении целых мюонных струй. В то же время, согласно Стандартной модели элементарных частиц, базирующейся на законах и следствиях специальной теории относительности, мюоны должны были появляться на расстояниях от оси пучка не б о ́ льших, чем 1–2 миллиметра.

Этот опыт однозначно свидетельствует о том, что поперечные размеры области взаимодействия элементарных частиц увеличиваются с ростом энергии этих частиц , вопреки предсказаниям специальной теории относительности.

А что говорит термодинамика?

Казалось бы, какое отношение имеет термодинамика к рассматриваемой здесь проблеме и чем она может помочь ее решению? Однако не стоит забывать, что эта наука, обладающая огромной степенью общности, уже поставила перед физиками немало вопросов, не все из которых получили убедительный и однозначный ответ. Напомним, в частности, что именно термодинамика явилась «повивальной бабкой» квантовой гипотезы, выдвинутой в 1900 г. М. Планком. И в отношении специальной теории относительности у этой науки также есть собственные выводы, которые, к сожалению, нередко игнорируются или замалчиваются.

Ясно, что развитие СТО не могло не затронуть термодинамику. В 1907 г. Планк [32] и Ф. Хазенорль [33] предприняли попытку пересмотра классической термодинамики с целью согласования ее с принципом относительности. В результате им удалось разработать релятивистскую формулировку термодинамики, на основе которой они вывели, в частности, формулы преобразования тепловой энергии (теплоты) и температуры. А именно, полагая, что два основных закона термодинамики справедливы в той системе отсчета, где рассматриваемая макросистема покоится, Планк и Хазенорль пришли к выводу, что энтропия этой системы является релятивистским инвариантом, а формулы преобразования для количества теплоты AQ и температуры T системы имеют вид:

AQ' = AqJ1- e ² ,

T' = TJl - e ² ,

где штрих обозначает величину, относящуюся к движущейся системе

отсчета. Согласно термодинамической отсчета, где данная Эйнштейн в статье

второй из этих формул, температура макросистемы всегда больше в той системе макросистема покоится. Примерно год спустя [34] поддержал доводы Планка и Хазенорля,

после чего соотношения (3) ни у кого из физиков не вызывали сомнений более полувека, повторяясь во всех учебниках и монографиях (см., например, [35,36]).

Однако в 1963 г. Г. Отт показал [37], что в ряде случаев формулы (3) приводят к физически некорректным, невозможным в природе результатам , и, также исходя из условия релятивистской инвариантности энтропии, установил, что, по его мнению, соотношения (3) следует заменить на

AQ ’ =

AQ

1- p ²

T' = ^= /1- р ²

Несколько позже к такому же выводу пришли, независимо от Отта, Х. Арзелье [38,39] и Т. Киббл [40]. Весьма подробно вопрос о законе преобразования количества теплоты и температуры был проанализирован К. Мёллером [41–43], который подтвердил корректность соотношений (4).

Справедливости ради следует отметить, что ряд ученых все еще продолжают отстаивать точку зрения Планка и, соответственно, формулы (3) (см., например, [44]), так что единый взгляд на релятивистскую термодинамику у физиков в настоящее время

отсутствует. Однако не надо забывать, что именно преобразования (3), в отличие от соотношений (4), приводят, как отмечалось выше, к физически некорректным результатам.

Но какое отношение имеют преобразования термодинамических величин к преобразованиям, связывающим пространственно-временные координаты событий в разных системах отсчета? Оказывается, самое прямое. Дело в том, что вывод соотношений (3) или (4) опирается на релятивистскую формулу преобразования элементарного пространственного объема ДУ макросистемы. При этом к равенствам (3) приводит предположение (вытекающее из преобразований Лоренца), что элементарные объемы в движущейся системе меньше, чем в такой же, но покоящейся системе, согласно закону ДУ' = ДУ

J

^^^^м

в ²

С другой стороны к равенствам (4) можно

очень просто (без значительных физико-математических ухищрений) прийти, предположив, что элементарные объемы в

результате перехода системы из состояния покоя в движение увеличиваются по закону

ДУ' =

ДУ

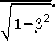
Заметим, что к равенствам (4) однозначно приводит решение уравнения Даламбера для электрического потенциала движущейся заряженной точечной частицы (если вид этого решения не подгонять формальными преобразованиями, как это часто делается [45], под результат, якобы согласующийся с СТО).

Что касается автора данной статьи, то он, являясь безусловным сторонником идеи объединения пространства и времени в единый комплекс пространство-время, но понимая его по-иному, чем Минковский, Эйнштейн и сторонники СТО, полагает, что релятивистские эффекты замедления времени, роста поперечных размеров частиц и др. являются отражением фундаментальных свойств не пространства-времени как такового, а самих частиц и связанных с ними физических полей. Как следствие, указанные релятивистские эффекты рассматриваются автором как реальные динамические, а не кинематические (как утверждает большинство сторонников СТО) эффекты. При этом он полагает, что признание эйнштейновской специальной теорией относительности динамического характера данных эффектов, по-видимому, невозможно, поскольку это привело бы данную теорию к ряду новых и, возможно, неразрешимых парадоксов.

Неужели поле жестко привязано к заряду?

Из формулы (2), в которой предполагается, что начало радиус-вектора г совмещено с движущимся зарядом, также следует, что электрическое поле, созданное этим зарядом, «перемещается» вместе с ним с той же скоростью и , оставаясь при любой скорости заряда симметричным относительно плоскости Σ, проходящей через заряд и перпендикулярной вектору и [9]. Иными словами, это поле кажется жестко « привязанным » к заряду .

У многих неспециалистов в СТО и электродинамике этот несколько неожиданный, парадоксальный результат вызывает недоумение, которое приводит, в лучшем случае, к сомнениям в корректности математического вывода формулы (2) и, как следствие, к ее отрицанию (полагаю, приводить здесь многочисленные ссылки на подобные работы было бы бестактно). Более того, на основе этого результата некоторые даже приходят к заключению об ошибочности электродинамики движущихся тел в целом. Это недоумение возникает из-за того, что в формуле (2) явно не отражен эффект запаздывания , обусловленный конечной скоростью распространения электромагнитных возмущений. Т.е. создается впечатление , что возмущение поля, вызванное движением заряда, не подвержено запаздыванию , несмотря на то, что в исходных уравнениях, из которых следует выражение (2), это запаздывание, несомненно, учитывается. Иными словами, с точки зрения обычного здравого смысла казалось бы , что поле движущегося заряда не должно быть симметричным относительно плоскости Σ, а выглядеть, например, так, как показано на рис. 1: «вектор напряженности поля должен возрастать [по модулю – СВМ ] впереди заряда и уменьшаться позади него, одновременно поворачиваясь назад» [46]. Симметрия же поля (2) относительно плоскости Σ, по мнению упомянутых исследователей, возможна лишь в случае «мгновенности» распространения электромагнитных возмущений.

Кроме того, стандартный математически строгий вывод выражения (2) не проясняет физические причины как указанной выше симметрии поля, так и его деформации по сравнению с полем покоящегося заряда. При этом ссылки на особые, релятивистские причины такого характера функции (2) [7–9,47,48] нельзя признать удовлетворительными, поскольку подобные ей зависимости описывают не только поле движущегося заряда в электродинамике, но и имеющие совершенно иную физическую природу поля в акустике и других областях физики. Это свидетельствует о том, что причина такого своеобразного характера функции (2) имеет единую, но отнюдь не релятивистскую (обусловленную, как утверждает специальная теория относительности, особыми свойствами пространства-времени) природу.

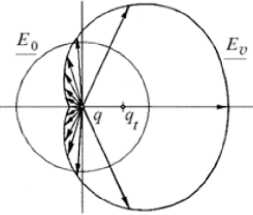
Рис. 1.

Целью данной работы является выяснение, путем исследования волнового поля, создаваемого равномерно движущимся точечным изотропным монохроматическим источником заданной частоты, во-первых, действительно ли существует « лоренцево сокращение длины » как динамическое явление и, во-вторых, действительно ли формула (2) ошибочна, не учитывая эффект запаздывания.

Cжат или растянут «эллипсоид Хэвисайда»?

Напомним, что выражение (2) является следствием решения неоднородного волнового уравнения (уравнения Даламбера) для скалярного потенциала ф (г, t) электрического поля, создаваемого движущимся зарядом в момент времени t в некоторой точке N(r) поля:

Δϕ -

1 дф = c ² д t

-

1 /- Р ⁽ r , t ),

^е о

,t

при учете соотношений А = "U ф,

Е = —V y

— ^t . Здесь Д= V² -

оператор Лапласа, р ( r, t ) - плотность заряда, А - векторный

потенциал поля. Такое же по структуре уравнение возникает и в ряде задач акустики [49,50] и других областей физики [51,52].

При заданной функции р ( r, t ) решение уравнения (6) имеет вид [7-

9,47]

ф ⁽ r , t ) =

4 пЕ о

JJJ

ρ

Г ‘ , t

-

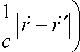
r - r ′

dr' ,

где интегрирование ведется по всему пространству. В данном выражении учитывается конечная скорость распространения возмущений поля, и поэтому его обычно называют запаздывающим потенциалом. Если заряд точечный, то р(г, t) = q 5[r'- r(t)], где r(t) = JU(t‘)dt' - уравнение траектории заряда, 5(...) - дельта- функция Дирака [53]. В этом случае [7–9,47]

Ф ⁽ r , t ) =

¹ __ q

^{4 п} Е о (    ( К -и )

I к--

I c где R=R(V) - радиус-вектор, проведенный из точки нахождения заряда в момент времени t, определяемый из равенства t = t — -(р", в рассматриваемую точку поля N(f), u = u(t ) - скорость заряда в тот же момент времени, (R • и) - скалярное произведение векторов R и и. Потенциал поля вида (8) называют потенциалом Лиенара – Вихерта.

Этот потенциал, как конечную скорость запаздывание .

видно из его определения, также учитывает распространения возмущений поля, т.е.

Если точечный заряд движется прямолинейно вдоль оси Ох декартовой системы координат с постоянной скоростью υ , то окончательное выражение для электрического потенциала ф (г, t)

поля принимает вид [1–7]:

Ф ⁽ r , t ) =

4 пе ₀

q

( п² )

( x -U t )² +1 1 -^ I ( у ² + Z ²) I c J

(где х, у, z - декартовы координаты отмечено выше, следует формула (2). Обратим внимание на выражение точки поля N), откуда, как

(9). Из него следует, что

эквипотенциальная поверхность, соответствующая значению потенциала ф = ф0, в случае неподвижного заряда (т.е. при и = 0) представляет собой сферу радиуса Ro = ^/4пгоФо с центром в точке х = 0. Теперь найдем форму эквипотенциальной поверхности, соответствующей тому же значению потенциала, в случае движущегося заряда. Полагая в формуле (9) ф = ф0 и учитывая выражение для Ro, мы приходим к уравнению

(^)²+®²<)²=1.             (10)

где

R*

R o

1-в'

= >R ₀ , , 2

в = и/с. Уравнение (10) - это уравнение двухосного эллипсоида, называемого «эллипсоидом Хэвисайда». Центр этого эллипсоида в любой момент времени совпадает с положением заряда, его малая полуось направлена вдоль вектора и и равна радиусу сферы Ro, а две одинаковые большие полуоси перпендикулярны данному вектору, причем их длины R* превышают значение Ro тем сильнее, чем больше скорость заряда, и при и ^ с они стремятся к бесконечности. Таким образом, оказывается, что эллипсоид Хэвисайда в действительности не сжат в направлении движения заряда, а, наоборот, растянут в перпендикулярном направлении. Это значит, что электродинамические причины для лоренцева сокращения длины тел в направлении их движения отсутствуют. Поэтому можно утверждать, что называемое «лоренцевым» сокращение длины движущихся тел, о котором говорится в специальной теории относительности, является чисто кинематическим эффектом, обусловленным, в основном, принятыми в этой теории правилами синхронизации и темпа хода и сверки показаний часов, находящихся в разных точках пространства и относящихся к разным системам отсчета.

Это значит, в частности, что принимая вместо правил СТО и преобразований Лоренца иные правила о градуировке и сверке показаний часов и принципиально возможные, но не удовлетворяющие принципу относительности преобразования пространственно-временных координат, относящихся к разным инерциальным системам отсчета, мы получим другие, отличающиеся от лоренцевых, соотношения между измеряемыми из разных ИСО размерами «покоящихся» и движущихся тел.

Но, может быть, формула (2) для напряженности электрического поля заряда приводит к другому результату? Проверим это. Зададим значение Ео модуля напряженности поля и найдем форму и размеры поверхностей, на которых |Е(г,-9)| = Ео при в = 0 и в > 0. В первом случае получаем сферу радиуса Ro = ^q/4ne0E0, а во втором уравнение искомой поверхности принимает вид

R ’ (У)

Данная поверхность

V ¹^²     r :

(1- P ²sin 2 fl)^{3/4 0}

представляет собой симметричный

относительно плоскости

£ и оси Ох , но деформированный

двухосный эллипсоид с

малой полуосью длиной

R = Ji—P " ^Ro

направленной вдоль вектора и , и большими полуосями, лежащими в плоскости £ и длинами R ^ = (1 — р ²) ^1/4R₀ . Таким образом, здесь R „ < R_o и R ^ > R_o, т.е. объем, ограниченный этой поверхностью, по сравнению со сферой радиуса R_o , действительно, сжат вдоль

направления движения заряда, но растянут в перпендикулярном направлении.

Однако судить об изменении размеров физических тел вследствие их движения на основании этого примера нельзя, поскольку все такие тела состоят из множества заряженных частиц, расстояния между которыми, а значит, и размеры тел, определяются из условия минимума потенциальной энергии системы частиц, которая, как известно, равна алгебраической сумме потенциальных энергий отдельных частиц, пропорциональных их электрическому потенциалу ф(г, t), а не E(f,t). Поэтому в основу анализа следует класть не выражения (2) и (12), а (9) и (10).

Вернемся к этим выражениям. Как мы видим, они свидетельствуют не о сжатии электрического поля заряда вдоль вектора и, а о его растяжении во всех направлениях, перпендикулярных этому вектору, в у = (1 — в2) 1/2 раз. Почему же тогда в учебной и научной литературе утверждается, что поле движущегося заряда сжимается? Ответ на этот вопрос прост: выражение (9) специально тождественно преобразуется так, во-первых, чтобы его новая форма позволяла увидеть в ней связь с преобразованиями Лоренца и, во-вторых, чтобы за счет появления масштабного множителя все размеры эллипсоида уменьшились в γ раз. Вот что говорит о выражении (9) Р. Фейнман [45]: «Это выражение становится более понятным [? – СВМ], если переписать его в виде

Ф ⁽т, t) =

4 пе ₀

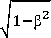
fy^ ■■■

V^-в2)   /

1/2 ■

(21.39)

В выражении (21.39) со всей ясностью предстает перед вами начало преобразований Лоренца X ^ ^ ut , У ^ у, z ^ z. ...

Но что можно сказать о добавочном множителе 1/

J

1- в ² ,

который

появился перед дробью в (21.39)? … Это – тот самый множитель, который появляется всегда, когда преобразуются компоненты

четырехвектора, так же как плотность заряда ρ преобразуется в e /J1 - в ² ».

Действительно, если не обращать внимания на «добавочный» множитель 1/ J1 - в ² , то из формулы (21.39) следует уравнение сжатого вдоль оси Ох эллипсоида:

(т?)² + (5² + 0² = 1'               (13)

где R** = Rq^ 1 — в2 < Rq. Но наличие этого множителя означает, что мы нашли эквипотенциальную поверхность, соответствующую не

J1

— в ² , в Y > 1 раз меньшему по

потенциалу ф ₀ , а потенциалу ф‘ = ф ₀

модулю, чем ф0. Т.е. реально, если иметь в виду численные значения заряда, расстояний и потенциала, переход от выражения (9) к (21.39) ничего не меняет, лукаво подгоняя полученный результат под принятые постулаты и принципы.

Что же касается утверждения Фейнмана о преобразовании плотности заряда как компоненты четырехвектора, то с математической точки зрения оно верно, но с физической в данном случае вызывает вопросы, поскольку здесь рассматривается точечный заряд с бесконечной плотностью, который остается точечным и в системе отсчета, движущейся вместе с зарядом.

Заметим, что если все же считать представление потенциала ф(т, t) в виде (21.39) адекватным отражением реальных физических процессов, в том числе реально существующего динамического q/^1 — в2

в

сжатия электрического поля, то тогда отношение формуле (21.39) следует трактовать как свидетельство увеличения электрического заряда движущейся частицы с ростом ее скорости. К такому же выводу автор ранее пришел из совершенно других соображений

[54], а именно, из необходимости согласования вытекающего из квантовой теории выражения для частоты излучения, испускаемого покоящимся атомом водорода, с релятивистской формулой

«замедления времени».

Итак, мы видели, что двум количественно эквивалентным и математически, по форме записи, отличающимся друг от друга лишь элементарным тождественным преобразованием (умножением на единичную дробь вида а/а ) выражениям можно дать принципиально разную физическую трактовку . Так, один из покоящихся наблюдателей может взять за основу формулу (9) и считать, что заряд движущейся частицы не изменился, а эллипсоид Хэвисайда растянулся в плоскости, перпендикулярной вектору скорости частицы и . Однако другой, также покоящийся наблюдатель, основываясь уже на формуле (21.39), вправе полагать, что заряд этой частицы увеличился, а эллипсоид Хэвисайда в той же пропорции сжался в направлении вектора и .

Приведем еще один простой пример такого рода. Рассмотрим две одинаковые частицы с зарядом q каждая, равномерно движущиеся в канале накопителя ускорителя с одинаковой скоростью υ рядом на расстоянии r друг от друга. Тогда с точки зрения наблюдателя в покоящейся лабораторной системе отсчета сила взаимодействия F. между этими зарядами равна геометрической сумме кулоновской силы

F_C и

силы

Лоренца F L : F . = qE + q [и X B ]. В рассматриваемом случае

I FC\ = — q T , 4п £ 0 r²

Ho f Ч и ) ц₀ q и

F, = q u B = q и ⁰      = ⁰

L             4n I r² ) 4n r²

и F = 1 q - ^f 1 4п £ ₀ r ² (

^^^^^^в

υ² c ²

Из

этой

формулы видно, что, как и было отмечено выше, взаимодействия между данными зарядами стремится к нулю сила

при

u ^ c .

Но на основании этой же формулы разные покоящиеся наблюдатели могут сделать разные выводы о причине такого ослабления взаимодействия. Одни могут считать, что эта причина обусловлена, уменьшением зарядов движущихся частиц по закону q' = q^ 1 - в- < q (здесь, как и прежде, в = и/ c). Другие могут полагать, что она состоит в увеличении расстояния между частицами по закону r' = r / д( 1 - р2 > r при q = const . Третьи, считая величины q и r неизменными, будут настаивать на том, что здесь проявляется влияние какого-то пока еще неизвестного фактора. Четвертые же, опираясь на следующее представление выражения для силы F :

F =      q - f l - ^U-) , где q ' = q /д/1 - в² >  q , r ' = r M - в^- >  r ,

E 4n£0 r'2 ( c2 J которое математически и количественно тождественно приведенному выше, также будут предполагать причиной ослабления влияние неизвестного фактора, но считать, что оно сопровождается увеличением зарядов частиц и одновременным пропорциональным ростом расстояния между ними.

Кто же из них прав? Дать ответ на этот вопрос можно только на основании аналитического сравнения выводов разных теорий с результатами соответствующих, но принципиально разных экспериментов, использующих разные физические принципы и методики измерения, при условии объективной и непредвзятой интерпретации этих результатов сторонниками разных теорий. При недостатке же или игнорировании подобной информации однозначный ответ на поставленный вопрос вряд ли возможен, поскольку тогда он неизбежно и в значительной степени будет основываться на вере исследователя в ту или иную научную концепцию.

Уравнение волнового поля движущегося точечного изотропного монохроматического источника и его решение

Итак, чтобы дать ответы на поставленные выше вопросы, исследуем характерные особенности волнового поля F (r, t), создаваемого в линейной, однородной, изотропной, недиспергирующей и недиссипативной среде соответствующим точечным изотропным монохроматическим источником фиксированной частоты ю0 = const, движущимся относительно данной среды с постоянной скоростью и = const. Заметим, что в зависимости от природы источника природа среды, являющейся основой для распространения соответствующих волн, может быть совершенно разной. Например, такой средой может быть однородная жидкость (или газ), источником волн в которой является акустический монополь. Возможно также, что существование такой среды может отрицаться (пример тому — так называемый эфир, являющийся средой распространения электромагнитных волн) или такая среда пока еще не обнаружена (здесь, согласно гипотезе автора, имеется в виду реальная материальная среда, возмущения которой мы называем волнами де Бройля, ошибочно придавая им лишь вероятностный смысл). В последнем случае источником волн является любая фундаментальная частица – электрон, протон и др. Дело в том, что согласно идее де Бройля [55], которая привела Э. Шрёдингера к формулировке его известных уравнений [56], ставших фундаментом современной нерелятивистской квантовой механики [57], с каждой фундаментальной частицей, имеющей не равную нулю массу покоя m , связан некоторый внутренний периодический процесс (внутренние колебания) с частотой ю0 = mc2 / й (где й — постоянная Планка), возбуждающий в окружающем частицу пространстве реальную волну.

В дальнейшем мы будем предполагать, что, несмотря на разнообразие типов сред, все они обладают перечисленными выше свойствами и, следовательно, распространение волн в них описывается одним и тем же волновым уравнением. Поэтому природу этих сред мы можем не конкретизировать, небезосновательно полагая, что решение этого уравнения правильно описывает распространение волн в любой из этих сред.

Итак, будем считать, что функция F(г,t), описывающая распространяющуюся волну, является решением неоднородного волнового уравнения (14), аналогичного уравнению для скалярного потенциала электрического поля (6):

д ² F д ² F д ² F 1 д ² F д x ² + д у ^{2 +} д z ² c² д t²

= 5 ( Г , t ),

где 5 (г, t ) — так называемая функция источников.

Пусть К0 - инерциальная система отсчета (СО), покоящаяся относительно рассматриваемой среды. Будем считать, что изотропность этой системы отсчета доказана, в частности, тем, что измеренное на опыте время распространения короткого волнового импульса «туда и обратно» до и от всех отражателей, расположенных на одинаковом расстоянии от источника, не зависит от направления на отражатель.

Введем в этой СО декартовую систему координат Oxyz , направив ее ось Ox параллельно вектору и вдоль траектории движения источника. В этом случае зависимость координат точечного источника от времени t выражается равенствами x = иt, у = z = 0, которые можно заменить дельта-функцией 5(г - иt) = 5(x - иt) 5(у) 5(z). Учитывая, кроме того, предполагаемый нами гармонический характер временной зависимости интенсивности источника от времени, функцию источников S(r, t) волнового уравнения запишем в виде:

S ( x , y , z , t ) = - 4 n F 0 5 ( x -и t ) 5 ( y ) 5 ( z )exp( i to ₀ t ), (15)

sω где F0 = ——- , 50 - амплитуда источника.

2 n c

Таким образом, волновое уравнение, описывающее волновое поле данного источника в рассматриваемой среде, принимает вид д2 F д2 F д2 F 1 д2 F                 „ „

—_т + —_т + —-_г---r^TT = ^{- 4 n F} o^{5 ( x -и} t ) ^{5 (} У ) ^{5 (} z ^)exP⁽ i ™o t ). ⁽¹⁶⁾

д x ²     д y ²     д z ² c ² д t²

Решение этого уравнения можно найти разными способами, например, используя преобразование Фурье [58] или с помощью метода, основанного на применении функции Грина [53]. Оно имеет вид [58]:

F ( x , y , z , t ) =

Fo exP

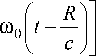
( n² Л

( x -и t )² +1 1 — ^ I ( у ² + z ²) I c )

где

R =

-

υ

— 1

c

υ

— ( x — U t ) +

c

2 I и ² V 2    2,

( x — и t ) +1 1 —     I ( У + z )

I c )

- расстояние от рассматриваемой точки M ( x , y , z ) поля до точки, где находился источник в тот момент времени, когда им был сформирован волновой фронт, достигший точки M в момент времени t .

Заметим, что при ю ₀ = 0 правая часть выражения (17), как и должно быть, совпадает (с точностью до размерного коэффициента) с правой частью формулы (9).

Для упрощения записи формул введем следующие обозначения: к ₀ =ю ₀/ c ; в = и/ c (| в|< 1); Р = V у ² + z¹ — расстояние от точки M поля до траектории движения источника (оси Ox ), р> 0; т = ct — временн а я переменная, выраженная в единицах длины; а ₀ — начальная фаза исходного рассматриваемого волнового фронта (относящаяся к моменту формирования данного фронта источником); значение а ₀ мы можем выбрать произвольно в промежутке [0; 2п]; O₅ ( t ) — точка с координатами x = и t , р = 0 , в которой в момент времени t находится источник.

В этих обозначениях выражения (17), (18) принимают вид:

F = F ( x , p , T ) =

F 0

V ( x -рт )² + (1 -P ²) p ²

exp ^[ ik 0 ^{( т}- R ) ] ,

R = (1 -p ²) ^{- 1} • Гр ( x -рт ) + V( x -Pt )² + (1 -P ²) p ² .

Исследование структуры волнового поля

Исследуем структуру волнового поля, задаваемого равенствами (19), (20). Сразу же отметим, что поскольку обе функции (19) и (20) явно зависят лишь от двух пространственных переменных – продольной координаты x и радиальной (перпендикулярной оси Ox ) координаты p , то волновое поле, созданное рассматриваемым источником, имеет радиальную симметрию относительно оси Ox , т.е. вид данного поля не изменяется при поворотах системы координат вокруг этой оси.

Выясним, что представляет собой картина волновых фронтов (являющихся, по определению, изофазными поверхностями , т.е. поверхностями с одинаковым значением фазы) данного волнового поля. Для этого рассмотрим серию следующих друг за другом фронтов, фазы которых отличаются на 2 п . Пусть n = 0,1,2,3, ... -номера фронтов в этой серии, и а ₀ - начальная фаза фронта с номером n = 0. Тогда фаза n -го фронта данной серии равна a _n = а ₀ + 2 п n , а момент времени t_n образования данного фронта на границе источника t n = (а₀ + 2п n ) / ю₀, чему соответствует значение т = т _n = ct n , р^авен

Tn = k-Ч^ + 2п n) (21) (в дальнейшем величины т, тn для краткости мы будем называть, как и t, tn, временем и моментами времени). В моменты времени тn (n = 0,1,2, ...) источник находился в точках On (т n) оси Ox с координатами xn =и tn = Рт n =т- (a0 + 2п n), У = z = 0, (22) k 0

и именно O n ( т _n ) - та точка, в которой был образован n -й волновой фронт рассматриваемой серии.

Найдем уравнение, описывающее геометрию этого фронта. Поскольку все точки каждого волнового фронта имеют одно и то же, соответствующее именно данному фронту, значение фазы, а фаза волны определяется показателем экспоненты (с отброшенным множителем i) в волновой функции F(x, y, z, t), т.е. в нашем случае величиной к0(т- R) в выражении (19), то уравнение n-го волнового фронта для произвольного момента времени τ представляет собой простое равенство к0 (т - R) = an = а0 + 2пn , (23) которое, с учетом формулы (21), можно представить в виде:

R =τ-τ n . (24) Подставив сюда выражение для R (20), после несложных преобразований находим явный вид уравнения n -го волнового фронта данной серии:

( x — вт n )² + р ² = ( т-т n )², (25) где n = 0,1, 2, ... , а т _n определяется формулой (21).

С геометрической точки зрения полученное уравнение является уравнением сферической поверхности радиуса r_n = τ-τ _n с центром в точке O n ( x = x_n = вт _n , y = z = 0).

Следовательно, точечный периодический источник частоты rn ₀, движущийся в однородной и изотропной среде с постоянной скоростью и, создает в этой среде волновое поле, в котором система волновых фронтов, сформированных данным источником в моменты времени t n = (а₀ + 2пn )/ю₀ (здесь 0 < а ₀ <  2 п , n = 0,1,2, ... , так что фазы соседних рассматриваемых фронтов отличаются на 2 п ), представляет собой совокупность вложенных друг в друга сфер с радиусами r_n , растущими со временем по закону r_n = c ( t - t_n ). При этом центры данных сфер лежат на траектории движения источника (а значит, и на оси Ox ) в точках O n ( т _n ) с координатами x n =и t n , находящихся на одинаковом расстоянии A x n = x n + 1 - x n = 2ли/ю₀ одна от другой (в тех же точках ось Ox пересекают перпендикулярные вектору и экваториальные плоскости о _ne рассматриваемой серии волновых фронтов).

Таким образом, изофазные поверхности волны, создаваемой движущимся точечным монохроматическим источником, т.е. ее волновые фронты, не испытывают никакого сжатия или растяжения при любой скорости движения источника и < c.

При этом каждый n -й волновой фронт, рожденный в точке x_n = υ t_n оси Ox в момент времени t_n , расширяется с постоянной скоростью c , сохраняя сферическую форму .

В дальнейшем будем считать, что ось Ox направлена в ту же сторону, что и вектор и, и поэтому 0 < в < 1. В момент времени t волновой фронт, соответствующий заданному значению n , пересекает ось Ox в точках xnf = ct - (c-u) tn , xnb = -[ ct - (c + u) tn ] ( xnb < xnf ), (26) называемых передним Pnf и задним Pnb полюсами, а его сечение экваториальной плоскостью σne представляет собой окружность Σ ne радиуса

P n ,max ⁽ t ) = r n = c ⁽ t ^- t n ) . ⁽²⁷⁾ При этом расстояния от переднего Δ x_nf и заднего Δ x_nb полюсов фронта до местоположения источника O s ( t ), которое он занимает в тот же момент времени t , равны соответственно:

^{A x}nf = x nf ^-U t = ⁽ c ^{-и )(} t ^- t n ) , A x nb =^U t ^- X nb = ⁽ c ^{+ u )(} t ^- t n ) . ⁽²⁸⁾ В этот же момент данный волновой фронт пересекает плоскость о s ( x = u t ) (которая также перпендикулярна вектору и, но проходит через точку O s ( t )) по окружности L s радиуса

P n , s ⁽ t ) = V ^{1 -в} 2 P n ,max = V С ^- —^u 2 ⁽ t ^- t n ) . (29) Заметим, что наблюдаемая длина волны λ , равная расстоянию между соседними волновыми фронтами рассматриваемой серии, перед движущимся источником (обозначим эту длину волны через X f ) оказывается меньше длины волны Х ₀ = 2 п c / ю ₀, образуемой покоящимся источником:

_ 2п c _ .

X f = x(n+1)f - Xnf =(1 — e) =(1 — e) Xo, (30) ®o а наблюдаемая длина волны λb за движущимся источником – больше X 0:

X b ^ X nb - X ( n + 1) b = (1 + в ) -^{n c} = (1 + в ) X 0 . (31) to o

Такое изменение длины волны (и частоты), происходящее вследствие движения ее источника, как известно, называют эффектом Доплера.

Теперь найдем распределение амплитуды распространяющейся волны на поверхностях волновых фронтов, соответствующих ее пучностям (такие волновые фронты для краткости будем называть А -фронтами), в произвольный фиксированный момент времени t >  t_n .

Согласно (19), где следует положить к ₀( т- R ) = 2 п n , амплитуда A волны, как функция координат и времени, в переменных ( x , р , т ), выражается формулой:

A ( x , p , T ) =

F о

V ( x -вт )² + (1 -в ²) p ²

В связи с поставленной задачей x, p, т в этом выражении теперь должны рассматриваться не как независимые переменные, а как пространственно-временные координаты некоторой точки произвольно выбранного нами (n-го) волнового фронта, т.е. как величины, связанные соотношением (25). Выразив из этого соотношения ρ :

Р ² = ^{( T-T} n ^{) 2} - ⁽ X ^-вт n ^{) 2} ,                       ⁽³³⁾

и подставив его в формулу (32), после ряда несложных преобразований получаем (с учетом того, что из равенства к ₀ ( т - R ) = 2 п n следует а ₀ = 0):

A n ( x , т ) =

F o

(1 -в ²)( T-T n ) -в ( x -рт ) ,

где через An обозначена амплитуда n-го А-фронта. Эта величина зависит от номера n данного фронта, времени и лишь одной координаты, поскольку значение другой координаты – в данном случае ρ – однозначно определяется значениями n , τ и первой координаты.

Из (34) следует, что при в > 0 и фиксированных значениях n, т частная производная дAn (x, т) / дx > 0, т.е. амплитуда An (x, т) является монотонно возрастающей функцией x , принимая значения от

A nb ( т ) =

F o

(1 + в )( т-т n )

^_ A n ,min ^{( т )}

на заднем полюсе Pnb рассматриваемого волнового А-фронта (x = xnb, р = 0) до значения

^A nf ^{( т )} =

F

(1 -в )( т-т n )

A n ,max ^{( т )}

на его переднем полюсе Pf (x = xnf-, p = 0). На экваторе Lne и в точках окружности Σs Α-фронта амплитуда возмущения равна, соответст- венно,

A ne ( т ) = —F ⁰

n

(при X = ^вт n , p = p n ,max )   и

A„ ,( т ) =-----y F °------

(1 -в ²)( т-т n )

(при ^x = ^вт , p = p n , , ) .

Легко видеть, что A_nf ≥ A_ns ≥ A_ne ≥ A_nb .

Заметим, что если бы источник покоился в точке x = 0, то амплитуда n -го А -фронта была бы одинакова во всех его точках, и в момент времени т равна, как следует из (34) при в = 0,

An (т) = —°-.(38)

^т-т n

Сравнивая значения A nf , A ns , A_ne , A_nb с A * ( т ), находим, что

A„*

An ,тах(т) = Anf (т) = —R > An , Ans (т) = —nJ > A„ , 1 -в

A

Ane (T) = An , An,min (т) = Anb (т) = j^-j < An •

Найдем расстояние O_sM_n = r_OM :

гом = VP2 + (x-вт)2 = V(т-тn)[(т-тn)-2вx+в2(т+тn)] .(40)

Для точек переднего и заднего полюсов n -го А -фронта, точек его экватора L _ne и окружности L s эти расстояния равны соответственно:

• rOM, f =Ax nf = (1 -в)(т-т n ) ,    rOM, b =Ax bf = (1 + в)(т-т n ),

• ^rOM , s =P ⁽ x , ^{т )} = Т1-Р ^{2( т-т} n ), r OM , e = P ⁽ x , ^{т )} = V ¹ + ^в 2 ^{( т-т} n ). (42) Чтобы картина волнового поля, формируемого движущимся монохроматическим источником, стала более полной и наглядной, найдем для произвольного фиксированного момента т >  0 уравнение поверхностей равной амплитуды, соответствующих её различным заданным значениям A_c (В дальнейшем поверхности равного уровня возмущения мы будем называть изобарами , а их частный случай – поверхности равной амплитуды возмущения – А - изобарами ). Для этого достаточно считать фиксированным значение амплитуды возмущения в формуле (32): A ( x , р , т ) = A c = const. В результате мы приходим к

  уравнению:

  
  

  ( x -вт )² + (1 -в ²) р ² = 1 - 0- 1

  I A c J

  
  

  .

  
  
  
  

Следовательно, искомые А -изобары представляют собой вложенные друг в друга и двухосные эллипсоиды ( эллипсоиды Хэвисайда ), растянутые в плоскости, перпендикулярной вектору скорости источника с полуосями a = ^{— 0} , а _р =-- ^{— 0}   >  a x и общим центром

A c        A c 71 -в ²

в точке O_s ( т ) .

Таким образом, поверхности равных амплитуд волны, создаваемой точечным монохроматическим источником, движущимся со скоростью и ^ 0 относительно изотропной среды, не совпадают с поверхностями равных фаз.

Это значит, чтот такие волны являются (по терминологии монографии [59]), неоднородными .

При этом следует нужно четко понимать, что при заданных значениях Ac, т, x = xc равенству (43) удовлетворяют лишь определенные точки единственного волнового А-фронта с фазой anc = 2пnc и номером n = nc

Т ( т-в x ) - ( F o / A c )

2 п c

1 — в ²

а именно, те точки, которые лежат на окружности Σ _nc , являющейся пересечением этого волнового фронта и плоскости x = x_c . (Формула (44) получается в результате подстановки в равенство (43) выражения для р ² из уравнения n -го волнового фронта (33), учета соотношения т _n = ct_n = (2 п c / ю ₀) n и решения полученного уравнения относительно n ). Если же координату x не фиксировать, то равенству (43), очевидно, будут удовлетворять точки, лежащие на окружностях, подобных Σ _nc , не одного А -фронта, а целой группы А -фронтов с номерами n и фазами a _n = 2 п n такими, что n c 1 ( т ) <  n <  n c ₂( т ). Таким образом, если сила источника гармонически зависит от времени, то изобары оказываются в некотором смысле условными , поскольку равенство (43) в этом случае выполняется не на единственной непрерывной двумерной поверхности, а лишь на системе криволинейных отрезков, принадлежащих различным А -фронтам.

Нетрудно убедиться в том, что аналогичные утверждения справедливы и для других волновых фронтов.

Запишем решение волнового уравнения (16), уравнение волнового фронта (25) и уравнение «поверхности» равной амплитуды (43) в движущейся со скоростью и системе отсчета К , связанной с источником, введя в ней сферические координаты ( r ‘ , Д ф ) с центром в точке O_s , в которой в этой системе отсчета покоится источник. Оставаясь в рамках классической волновой теории, будем считать, что координаты такой системы связаны с координатами ( x , р) равенствами:

x = вт + r' cos Д , р = r' sin Д . (45)

Подставив эти выражения в преобразований получаем величины R :

формулы (19) и (20), после несложных для волновой функции F ( r ', A , т ) и

F ( r ',^,т) =

F 0

r' J 1 - p²

== exp ^[ iko(T ^- R ^)] = ■ sin² ^

F 0

r' 1 - p² sin² У

exp ⁱ to o t

_ к

^^^^^^s

r c ф (У, в) V

,

или

F ( r ', A , т ) = ^7" P ( A ; P ) exp i to ₀ t

r

к

^^^^^^e

r ‘

c ф ( A , P ) J_ .

Здесь

R = r

, P cos A + 71 -P 2 sin² A

к

к

1-P2

P ( A ; P ) =

V

= r'

c

к c ф (A, P) J,

71 -P ² sin² A

– зависящий от угла

A и скорости и = P c

частицы поправочный

амплитудный коэффициент, появившийся в результате перехода из изотропной системы отсчета К0 в движущуюся относительно среды систему отсчета К' , c ф (A, P) = c (71 -P2 sin2 A -P cos a) (50) — также зависящая от A и и скорость волны в системе отсчета К, равная скорости переноса энергии волной в данном направлении. Заметим, что это же выражение для cф (A) непосредственно следует из векторного равенства с,ф = с - и с учетом того, что A есть угол между векторами и и Еф.

В системе отсчета К ' уравнение волнового фронта, представляющего собой сферу с центром в точке с координатами r' = -P ( t - т n ), A = п , и уравнение изобары принимают, соответственно, следующий вид:

^г П = ⁽7 ^{1 -}Р ^2sin 2 ^A-Р ^{cos A}J ^{( т-т} n ) = ^c ф ^{( A} , P ^{)( t - t} n ), ⁽⁵¹⁾

, F ⁰ ₂ , ₂   = F ⁰ p ( A ; P ).                    (52)

A_c 71 -P ² sin² A    A c

Распределение амплитуды возмущения A n ( A , t ) по поверхности n -го волнового фронта в момент времени t в этом случае определяется выражениями

A n ( A , t ) = -A- K ( A ; в ),                    (53)

C ⁽ t ^- t n )

где

K ( A ; в ) = 1 -в д/1 -в ² sin² A cos A-в ² sin² A

- 1

.

Легко показать, что функция K(A) монотонно убывает с ростом угла A, принимая при A = 0 (т.е. на переднем полюсе волнового фронта) свое максимальное значение Kmax = (1 — в)-1, а при A = n (на заднем полюсе фронта) минимальное значение Kmin = (1 + в)-1; при A = п/2 значение этой функции равно (1 — в2)-1, при этом чем ближе значение β к единице, тем сильнее выражен перепад возмущения на полюсах волнового фронта. Все эти выводы находятся в полном соответствии с результатами, полученными выше.

Обсуждение результатов

Подводя итог проведенному исследованию свойств волнового поля (19)–(20), можно сделать следующие выводы. Каждый волновой родной и изотропной среде, является сферическим , и в системе отсчета, связанной со средой, расширяется от точки своего формирования источником во всех направлениях с одной и той же скоростью c , не зависящей от скорости υ движения источника .

При этом при и ^ 0 возмущение среды в различных точках одного и того же волнового фронта оказывается, вообще говоря, различным, так что ни один из волновых фронтов не является изобарной поверхностью, т.е. поверхностью равного уровня возмущения среды, в частности, поверхностью равной амплитуды возмущения . В этом случае максимальное возмущение среды достигается на переднем полюсе (определяемом по направлению вектора и) сферического волнового фронта, а по мере смещения рассматриваемой точки вдоль «меридиана» данного волнового фронта возмущение монотонно уменьшается, достигая своего минимального значения на противоположном, заднем полюсе этого фронта .

В частности, согласно соотношениям (39), в любой заданный момент времени t амплитуда An (t) возмущения от движущегося источника достигает своего максимального значения An,max(t) на переднем полюсе Pnf А-фронта, имеющего данный номер n ; при этом она в (1 -в) 1 раз превышает амплитуду A* возмущения, создаваемого таким же, но покоящимся источником, помещенным в точку On (tn), в которой был образован данный фронт, и являющуюся его центром. Иначе говоря, эта амплитуда оказывается равна амплитуде Af* возмущения, которое создал бы такой же по силе покоящийся источник, помещенный в точку Os (t), в которой в данный момент времени находится движущийся источник, т.е. ближе к данному полюсу, чем центр On (tn) рассматриваемого фронта. Наоборот, на заднем полюсе Pnb того же фронта амплитуда возмущения An (t) минимальна. А именно, как показали наши расчеты, ее значение An,min(t) оказывается в (1 + в) 1 раз меньше

*

амплитуды An возмущения, создаваемого таким же покоящимся источником, помещенным в центр On (tn ) данного фронта, и равно лишь относительно небольшой амплитуде

**

A_b   возмущения,

создаваемого таким же покоящимся источником, находящимся в точке O s ( t ) реального местоположения движущегося источника в момент t, т.е. дальше от данного полюса, чем исток O n ( t n ) рассматриваемого фронта.

По мере смещения рассматриваемой точки M _n вдоль «меридиана» сферического волнового фронта от его переднего полюса в к заднему амплитуда A_n монотонно уменьшается, однако в точках передней полусферы фронта она остается больше значений A “( x , t ) и A * , сравниваясь с величиной A * на экваторе фронта. В точках задней полусферы фронта амплитуда A_n по-прежнему монотонно убывает при приближении к заднему полюсу, оставаясь больше A ** ( x , t ), но меньше A * . Это обусловлено, в частности, тем, что при смещении точки M _n вдоль «меридиана» от полюса P_nf к полюсу P_nb расстояние O s M_n возрастает, а амплитуда A “( x , t ), тем самым, убывает быстрее, чем происходит соответствующее уменьшение амплитуды A n ( x , t ), обусловленное движением источника.

Таким образом, движение изотропного источника в однородной и изотропной среде не влияет на форму волновых фронтов: они остаются сферическими и расширяются с постоянной скоростью c , а значит, возмущение в такой среде распространяется во всех направлениях с одинаковой конечной скоростью. Однако его движение влияет на распределение уровня возмущения среды вдоль волновых фронтов: в передней полусфере каждого волнового фронта возмущение оказывается больше, а в задней полусфере меньше по сравнению с его уровнем, достигаемым на волновом фронте, имеющем ту же фазу, но образованном покоящимся источником; при этом экваториальная плоскость фронта, разделяющая данные полусферы, в любой момент времени t лежит за источником на расстоянии c(t - tn) от него. В результате уровень возмущения среды оказывается больше его уровня при неподвижном источнике не только перед источником, но и в определенной области пространства за ним.

Кроме того, как видно из равенства (32), распределение амплитуды возмущения оказывается симметричным относительно плоскости x = υ t , проходящей непосредственно через движущийся источник, а в точках, лежащих на траектории движения источника (т.е. на оси Ox ), оно в каждый момент в точности такое же , как и создаваемое источником, покоящимся в точке x = υ t :

A ( x, р = 0, t ) =

F o

x - υ t

Однако в точках плоскости x = и t амплитуда возмущения при и ^ 0 оказывается больше , чем в случае покоящегося источника:

1 I F

A( x = u t , р , t ) = ,       ------.                         (56)

1 -в^ P

Таким образом, чем больше скорость источника, тем больше амплитуда возбуждаемого им волнового поля в плоскости x = υ t , меньше расстояние между пучностями волны перед ним и больше – за ним. При |u| ^ c (|₽|^ 1) амплитуда волны, как видно из формулы (17), все слабее зависит от радиального расстояния ρ , возмущение захватывает все большую площадь в плоскости x = υ t и при | и | = c, когда расстояние X f между пучностями волны перед источником становится равным нулю (это значит, что все сферические волновые поверхности соприкасаются своими передними полюсами), данная волна превращается в плоскую ударную волну [60,61] (здесь мы не будем касаться случая | и | >  c ).

Подчеркнем, что, как следует из приведенных выше формул, все эти закономерности имеют место при любых значениях частоты источника ю0, в том числе и в предельном случае ю0 ^ 0, в котором решение уравнения (6), согласно формуле (50) при k0 = ю0/ c = 0, принимает вид:

F ( x , p , t ) =

F о

V⁽ x -^{вт )2} + о -^{e 2) p}

, или

F ( x , y , z , t ) =

F

.

2 Л

( x -и t )² + 1--_г |( у ² + z ² )

V I ^c )

А поскольку формула (57) совпадает (при учете формальных замен F ₀ ^ q , F ^ф ) с выражением (9) для распределения

потенциала ϕ точечного электрического заряда q , движущегося с постоянной скоростью, то практически все, сказанное выше, можно отнести не только к монохроматическому, но и к постоянному движущемуся источнику, если под волновыми фронтами понимать не реальные, формируемые волной, а аналогичные по смыслу условные поверхности.

Для сравнения на рис. 2 и 3 приведен характерный вид (в плоскости Oxy ) волнового поля, образованного покоящимся источником (рис. 2) и источником, движущимся со скоростью и = 0,75 c (рис. 3).

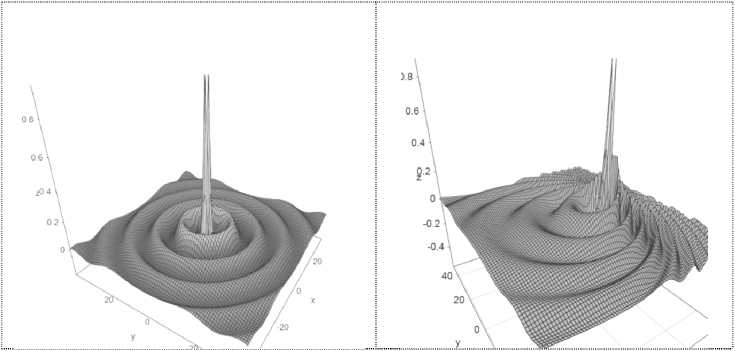
Рис. 2                          Рис. 3

Волновое поле движущегося источника, в = 0,75

Волновое поле покоящегося источника, в = 0

Таким образом, упомянутое во «Введении» впечатление о том, что возмущение электрического поля, вызываемое движущимся зарядом, не подвержено запаздыванию, жестко «привязано» к заряду и при любой его скорости движется вместе с ним, хотя и в сжатом в направлении движения заряда виде, как следует из сказанного выше, является ложным. Этот же вывод относится также и к акустическому полю и другим полям, описываемым уравнением вида (1). А именно, в выражениях (9), (57) не только корректно учитывается запаздывание, но также учитывается и перераспределение возмущения (или потенциала поля) в пределах каждой из волновых поверхностей. При этом данное перераспределение является следствием, с одной стороны, движения источника, а с другой – также конечной скорости распространения возмущения, т.е. его запаздывания.

Чтобы последнее утверждение стало более понятным, рассмотрим следующую простую модель. Предположим, что величина F в уравнении (14) имеет физический смысл избыточной концентрации неких «частиц», а роль источника, описываемого правой частью этого уравнения, состоит в том, что он периодически, по закону ~ F₀ cos( m ₀ t ), выбрасывает в пространство порции этих частиц, которые затем удаляются от него равномерно во все стороны с постоянной относительно системы отсчета К ₀ скоростью, не зависящей от скорости источника. Очевидно, в этом случае как среднее по относительно небольшому объему пространства Δ V , так и амплитудное (в том же объеме) значения концентрации частиц, вообще говоря, будут убывать по мере удаления от источника. И если источник покоится, то расстояния в радиальном направлении между соседними порциями частиц будут оставаться неизменными, в результате чего (амплитудное) распределение концентрации частиц в пространстве установится обратно пропорциональным квадрату расстояния r до источника. Однако при движении источника картина становится иной . А именно, в направлении перед движущимся источником каждая последующая порция частиц теперь выбрасывается ближе к предыдущей порции на некоторое расстояние А х = иАа / ю ₀ =в^ ₀( Аа / 2 п ), а в противоположном направлении – дальше от предыдущей порции на такое же расстояние (здесь Δα – разность фаз источника в моменты выбрасывания данных порций частиц). Поэтому концентрация частиц в объеме Δ V , в том числе ее амплитудное значение, перед движущимся источником оказывается выше, а за ним – ниже, чем в случае покоящегося источника.

Заметим, что в этом иллюстративном примере существенное значение может иметь величина продольного (в направлении от источника) размера объема А V , т.е. его длина A l. Если выброс частиц источником предполагается, как мы считали выше, непрерывным процессом, происходящим по закону ~ F 0 cos( rn ₀ t ), то для обнаружения изменения концентрации частиц достаточно взять A l = Х 0 = 2 п c / ю ₀. Если же источник выбрасывает частицы очень короткими импульсами, следующими друг за другом с некоторой скважностью A t , то распределение концентрации частиц в пределах каждого расширяющегося сферического волнового фронта будет однородным , и обнаружить изменение их средней концентрации в системе таких фронтов можно будет лишь при условии A l >>  иА t.

Подчеркнем, что физическая природа «частиц» в данной модели несущественна: в каждом конкретном случае она может быть уникальна, важно лишь, чтобы их скорость была постоянна и не зависела от скорости движения источника. Так, например, подобными «частицами» могут быть частицы газа, если речь идет о нагнетании этого газа в пространство; в других случаях под ними можно понимать фотоны, кванты энергии, виртуальные кванты того или иного физического поля и т.д.

Более того, наличие реального потока материальных или виртуальных частиц для объяснения картины волнового поля вовсе не обязательно. Например, в акустических волнах волновой перенос энергии от источника фактически происходит без макроскопического (на расстояния, большие длины волны) перемещения частиц среды (слабый акустический ветер является нелинейным эффектом, и к рассматриваемым нами линейным задачам он не имеет отношения). Тем не менее, здесь также имеет место исходящий от источника поток, однако это не поток частиц, а поток энергии, от локального значения плотности которого зависит плотность энергии е в данной точке пространства и, в итоге, амплитуда акустической волны. При движении изотропного источника звука плотность потока энергии j от него изменяется, достигая максимального значения в направлении вектора и и возрастая, в целом, во всем полупространстве перед источником. Наоборот, в полупространстве за источником плотность потока энергии уменьшается, принимая свое минимальное значение в направлении, противоположном вектору и. При этом плотность энергии непосредственно перед источником увеличивается настолько, что образуется ее значительный градиент в направлении, перпендикулярном вектору скорости источника, вследствие чего избыточная энергия «растекается» преимущественно в этом направлении. В результате амплитуда волны, пропорциональная „1/2

е , возрастает не только непосредственно впереди источника, но и в радиальном направлении, достигая максимального значения в плоскости x = υ t . Таким образом, поскольку скорость передачи акустической энергии (равная скорости звука) конечна и не зависит от скорости движения источника, то распределение плотности энергии в среде, зависящее от потока энергии, изменяется не только по причине ее рассеяния, но и вследствие движения источника, влияя тем самым на локальные значения амплитуды акустической волны.

По мнению автора, в общем случае можно утверждать, что именно существование потока реальных или виртуальных частиц, потока энергии или иного рассматриваемого в физике потока, генерируемого изотропным источником и характеризующегося конечностью и независимостью скорости этого потока от скорости движения источника, является основной и необходимой причиной необычного, на первый взгляд, характера волнового поля, образуемого подобным источником при его движении. При этом плотность данного потока должна быть главным фактором, влияющим (возможно, опосредованно) на амплитуду рассматриваемой волны.

Таким образом, перераспределение амплитуды возмущения как по различным волновым А-фронтам, так и по поверхности каждого такого фронта в рассматриваемой нами задаче обусловлено прежде всего изменением длины волны λ (т.е., фактически, эффектом Доплера), которая при движении источника становится функцией переменных (r', А) (в системе отсчета К). Однако не исключено, что немаловажную роль в формировании вида волнового поля играет и некий закон сохранения, который в рамках рассмотренной выше модели можно трактовать как закон сохранения числа характерных для данной физической системы «частиц» – квантов соответствующего поля. В пользу этого утверждения свидетельствует следующее обстоятельство. Если функции F в уравнении (14) приписать смысл физической величины, пропорциональной плотности числа некоторых условных (природа которых не оговаривается) «частиц-квантов» в пространстве, то интеграл от функции F (r ' , А, т) по объему АV = Аr‘ -Аа (где Ао = const), выделенному в сферическом слое волны переменной толщины Ar' = Х(r‘ , А), включающем волновой А-фронт, не зависит от местонахождения этого объема в данном слое. Это проявляется, в частности, в том, что оказываются справедливы равенства

AKf =-- F^ (1 - в )^0 = A„ъКъ =-- F^ (1 + в )^0 = F^ , (58) nf nf (1 -в )( Т-Т n ) '       ⁰ nb nb (1 + в )( Т-Т n ) ^{V 0} T-т n ’ ^{V 7}

которые следуют также и из соотношений (30), (31), (35), (36).

Обратим внимание еще на одно обстоятельство. Дело в том, что для физически корректного перехода от интегрального выражения (7) к формуле Лиенара – Вихерта (8) необходимо предполагать, что заряженная частица имеет конечные размеры и ее заряд каким-то образом распределен в конечной области пространства, так что p(r,t) * q5(r - r0(t)) [2,4]. Действительно, в противном случае из (7)

следует, что

Ф ⁽ r , t ) =

q

4 пе ₀ j? ( t ') ,

—* —*

где, как и в формуле (8), R = R ( t ‘ ) - радиус-вектор, проведенный из точки нахождения заряда в более ранний (по сравнению с t )

R ( t ') момент времени t ′ , определяемый из равенства t = t -     ,

в

c рассматриваемую точку поля — .

Р. Фейнман по этому поводу пишет следующее: «На первый взгляд кажется (и почти все так и подумают), что ответ состоит в том, что интеграл от ρ по такому «точечному» заряду равен просто общему заряду q , т.е. что [справедлива формула (94) – СВМ]. … Но эта формула ошибочна. Правильный ответ такой: [далее приводится формула Лиенара – Вихерта (8) – СВМ]» [45, с. 156]. Затем Фейнман вычисляет интеграл (7) для, как он говорит, ««точечного» заряда в форме небольшого заряженного кубика». Получив формулу (8), он пишет: «Появился поправочный множитель. Он появился потому, что в то время, как наш интеграл «проносится над зарядом», сам заряд движется. … Наконец, поскольку размер заряда не вошел в окончательный итог, то тот же результат получится, если заряд стянется до любых размеров, вплоть до точки.» [45, с. 159–160].

Аналогичное объяснение особенностей интегрирования в формуле (7) дают В. Пановский и М. Филипс. Кроме того, они указывают, что «если для вычисления потенциала в выражение (7) подставить плотность ρ , взятую в соответствующий момент, то интеграл JJJ р( t ') dV не будет равен полному заряду системы.

Причина этого заключается в том, что различные слагаемые в подынтегральном выражении берутся в различные моменты времени. Пока сфера радиуса R = c ( t - 1 ‘ ) проходит по распределению зарядов, последние могут сдвинуться так, что будут более плотными, чем те, которые дали бы правильный полный заряд» [8, с. 314 ].

Итак, с одной стороны, стандартный вывод формулы запаздывающего потенциала Лиенара – Вихерта (8), по сути, основан на предположениях об отсутствии точечных зарядов и однородном или сферически симметричном распределении заряда в пределах частицы. При этом возможность применения данной формулы к точечному заряду базируется лишь на том, что при указанных выше предположениях о виде функции р ( r ) в эту формулу размеры частицы не входят. С другой стороны, последующий затем вывод выражения (9) из формулы (8) предполагает, наоборот, что рассматриваемый заряд является точечным . Это противоречие является одной из причин нередко высказываемых сомнений в корректности учета запаздывания в современной электродинамике движущихся сред (см. множество сообщений на сайтах, посвященных «альтернативной физике»).

Однако, на взгляд автора, указанное противоречие имеет не физическую, а чисто математическую причину, и связано оно с особенностями определения дельта-функции Дирака, которая представляет собой предел , к которому стремится определенный класс функций при стремлении входящего в них параметра к нулю или бесконечности. А поскольку операции предельного перехода и интегрирования, вообще говоря, не коммутативны, возникает необходимость в промежуточной замене при интегрировании δ -образного распределения плотности заряда на распределение, «размазанное» по пространству.

О том, что данное противоречие кажущееся и несущественно с физической точки зрения, может свидетельствовать, в частности, вывод формулы (9), основанный на прямом решении уравнения (16) с использованием очевидных замен переменных.

Гипотеза о природе астрономического эффекта Козырева - Насонова

Интересно, что решение волнового уравнения (16), выражающееся формулами (19), (20), может, по-видимому, вполне естественным образом объяснить кажущиеся невероятными (и потому сомнительными) результаты астрономических наблюдений, выполненных в 50–60-х годах прошлого столетия Н.А. Козыревым и В.В. Насоновым [62,63]. Напомним, что они наблюдали в телескоп-рефрактор различные космические объекты – звезды, шаровые скопления, галактики. При этом ими сначала регистрировалось местоположение видимого (оптического) изображения наблюдаемого объекта. Затем фокальная плоскость телескопа закрывалась специальным металлическим экраном с подвижной узкой щелью, за которой находился разработанный этими учеными особый датчик. Щель медленно смещалась от видимого положения объекта в том или ином направлении на расстояние в несколько десятков угловых секунд. При этом оказалось, что при некотором определенном положении щели, соответствующем направлению на то местоположение данного объекта на небесной сфере, которое он занимал бы, если бы свет от него в направлении Земли распространялся мгновенно , датчик отчетливо регистрировал сигнал (правда, несколько размытый). Иными словами, Козырев и Насонов для каждого из наблюдавшихся ими объектов зарегистрировали, во-первых, световой сигнал (т.е. электромагнитную волну), идущий от места, которое данный объект занимал в далеком прошлом (в момент испускания им дошедшей до земного телескопа волны), и, во-вторых, сигнал неустановленной природы, идущий от места, где данный объект реально находится в момент его наблюдения .

Результаты своих опытов Н.А. Козырев и В.В. Насонов рассматривали как экспериментальное подтверждение некоторых выводов разрабатывавшейся Козыревым теории о физических свойствах времени, названной им причинной механикой . Согласно этой теории, в природе, кроме обычного взаимодействия, когда одно тело действует на другое с помощью известных силовых полей, распространяющихся в пространстве с конечной скоростью, существует и другой, мгновенный способ передачи действия («событийного сигнала»), осуществляемый вдоль гиперповерхности одномоментных событий благодаря особым физическим свойствам времени [64]. К сожалению, теория Козырева осталась незавершенной, а ее доказательная база недостаточно убедительной.

По мнению автора данной статьи, результаты астрономических наблюдений Козырева и Насонова неудивительны и имеют очень простое объяснение. Действительно, волновое уравнение (16) можно рассматривать как простейшую теоретическую модель, описывающую излучение удаленной звезды в некотором узком интервале частот. Тогда показатель экспоненты в решении этого уравнения, т.е. в формуле (17), определяет фазу испускаемой звездой световой волны, в равенство (25) - форму волнового фронта , представляющего собой сферу с центром в точке, где находился источник (звезда) в момент формирования этого фронта , т.е. в далеком прошлом. Амплитудный же фактор в этом решении определяет форму эффективной эквипотенциальной поверхности (изобары), которая оказывается симметричной относительно плоскости, перпендикулярной вектору скорости звезды и проходит в любой момент времени через мгновенное положение источника в этот же момент (здесь под эффективной эквипотенциальной поверхностью понимается изобара, которая представляет собой усреднение «мгновенных» изобар по промежутку времени, превышающему период колебаний источника; как нетрудно показать, ее форма с очень большой точностью описывается уравнением (57)).

С другой стороны, как известно, оптическое изображение источника света в телескопе, как и в других оптических системах, содержащих линзы и зеркала, создается за счет определенного изменения формы волнового фронта падающей волны, приводящего к тому, что энергия излучения, первоначально распределенная (в пределах передней поверхности линзы-объектива) по этому фронту, концентрируется в небольшой области в фокальной плоскости линзы [65]. В частности, оптическое изображение «бесконечно» удаленного источника (звезды) в телескопе образуется вследствие деформации объективом (или зеркалом) телескопа практически плоского фронта падающей волны, параллельного главной оптической плоскости объектива, и концентрации световой энергии, дошедшей от звезды до телескопа, в его фокусе, что позволяет помещенным там сенсорам (фотопленке, фотоэлементу, специальному датчику, сетчатке глаза наблюдателя и т.п.) зарегистрировать данное излучение. При этом направление нормали к данному волновому фронту (а значит, и направление оптической оси телескопа) совпадает с направлением на ту точку в пространстве, в которой данный фронт был сформирован источником, т.е. в точку, в которой находилась звезда в момент испускания того самого «фрагмента» света, который много лет спустя после своего «рождения» попал в телескоп наблюдателя. Таким образом, телескоп фиксирует «запаздывающее» направление, задаваемое фазой волны, т.е. показателем экспоненты в решении волнового уравнения.

Однако, согласно гипотезе автора, при определенных условиях (например, при использовании специальных датчиков) с помощью обычного телескопа, по-видимому, можно зарегистрировать и второй , плохо сфокусированный, а потому слабый сигнал от звезды, обусловленный не фазовым, а амплитудным фактором решения (17). Направление, определяемое этим сигналом как направление нормали к эквипотенциальной поверхности излучения в точке наблюдения, совпадает с направление на истинное положение звезды в пространстве в момент ее наблюдения . Именно такой сигнал и такое направление на его источник, по мнению автора, и было зарегистрировано в опытах Козырева и Насонова.

Заметим, что, как следует из вышесказанного, для уверенной регистрации второго, кажущегося мгновенным сигнала необходимо создать особую фокусирующую систему, которая осуществляла бы фокусировку падающей волны путем деформации не ее волнового фронта, а эквипотенциальной поверхности (изобары) этой волны (такая система в опытах Козырева – Насонова отсутствовала). Кроме того, особое значение здесь может иметь методика регистрации данного сигнала и, в частности, свойства материала, конструктивные особенности и чувствительность используемых датчиков.

Конечно, результаты опытов Козырева – Насонова нуждаются в тщательной проверке. Однако приведенные выше соображения говорят в пользу реальности этих результатов, снимая с них налет фантастичности. Во всяком случае, очевидно, что если эффект Козырева – Насонова окажется реальным, он станет мощным инструментом как в астрономических, так и в чисто физических исследованиях.