Декомпозиция электромеханической системы механизма подачи трубы стана ХПТ-450

В статье рассматривается метод декомпозиции электромеханической системы (ЭМС) механизма подачи трубы стана ХПТ-450. Он позволяет выделить наиболее значимые элементы системы и определить, какие параметры конструкции требуют изменения. Метод декомпозиции основан на частотных характеристиках. Авторы отдают предпочтение асимптотическим логарифмическим частотным характеристикам, поскольку они обеспечивают прямой выход на параметры конструкции.

Метод предусматривает следующие операции:

• 1.    Получение математического описания системы в виде структурной схемы, состоящей из звеньев не выше первого порядка.

• 2.    Анализ влияния отдельных звеньев, контуров и связей на систему по частотным характеристикам.

• 3.    Нормирование структурной схемы.

Стан холодной прокатки труб ХПТ-450 предназначен для производства холоднокатаных труб из легированных углеродистых сталей с переменной толщиной стенки трубы диаметром до 450 мм. Такие трубы используются в атомной энергетике и авиационной промышленности. Привод подачи трубы выбран среди других механизмов поворот-но-подающей группы потому, что технология предъявляет к нему наиболее жесткие требования, а стан ХПТ-450 - самый крупный стан холодной прокатки, и многие его параметры и режимы работы предельные и представляют научный интерес.

• 1.    Структурная схема системы

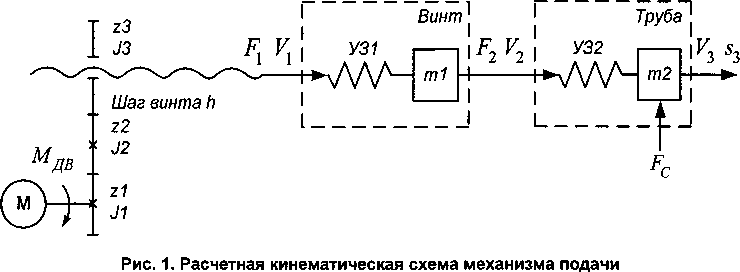
В кинематической модели механизма (рис. 1) учтены податливость трубы и винта. При анализе системы сделаны следующие допущения [3]:

• а)    силы и моменты приложены к сосредоточенным массам т\ и ти2;

• б)    упругие звенья У31 и У32 невесомы и характеризуются коэффициентами жесткости Ci и С₂;

• в)    деформация упругих звеньев линейна и подчиняется закону Гука.

• 2.    Частотный анализ

Структурная схема математической модели механизма показана на рис. 2. На схеме п^ - скорость вращения двигателя; М_№ М_с - электромагнитный момент двигателя и момент сопротивления; J - момент инерции вращающихся частей; F_b F₂ - силы реакции винта и трубы; ц_вп - КПД винтовой передачи; F_c - сила сопротивления поступательному движению; К_ь К₂, У₃ - линейные скорости концов винта и трубы; т_ь т₂ - массы винта и трубы; С_ь С₂ - коэффициенты жесткости винта и трубы; s₃ - перемещение конца трубы.

Коэффициент жесткости винта Ci равен 26-10⁷ Н/м. Коэффициент жесткости трубы, в зависимости от размеров, находится в диапазоне от 9Ю⁷ до 275-10⁷ Н/м. Поступательная масса механизма подачи /Mi равна 17 500 кг, а масса трубы т₂ находится в диапазоне от 355 до 2800 кг. Значения остальных параметров приведены в [4].

В работе рассмотрены три типа электродвигателей. В качестве исходного варианта была взята модель синхронного двигателя с векторным управлением, примененного ВНИИэлектроприводом на стане ХПТ-450П1 ОАО ЧТПЗ. Для обобщения ре зультатов рассмотрены другие модели синхронных двигателей, в том числе серии МТ, МТМ, МТВ краново-металлургических асинхронных двигателей, работающих в синхронном обращенном режиме.

Среди машин постоянного тока рассматривались серии металлургических двигателей Д, ДП, МП, П; среди асинхронных - широко распространенная серия 4А и новая серия RA. Двигатели взяты мощностью от 50 до 500 кВт [3, 4].

На втором шаге методики проведем предварительный частотный анализ и рассчитаем частоты среза локальных контуров. Локальные контуры -это контуры без перекрестных обратных связей, т.е. без учета влияния соседних контуров [2].

Контур / (контур саморегулирования ЭДС двигателя) образован звеном якорной цепи, звеном момента инерции двигателя и обратной связью по ЭДС. Этот контур учитывает статические и динамические свойства вращающихся механических масс двигателя и редуктора.

Контур II (контур электромеханической связи [5]) образован звеньями момента инерции двигателя, упругости винта и отрицательной обратной связью по реакции винта F_b

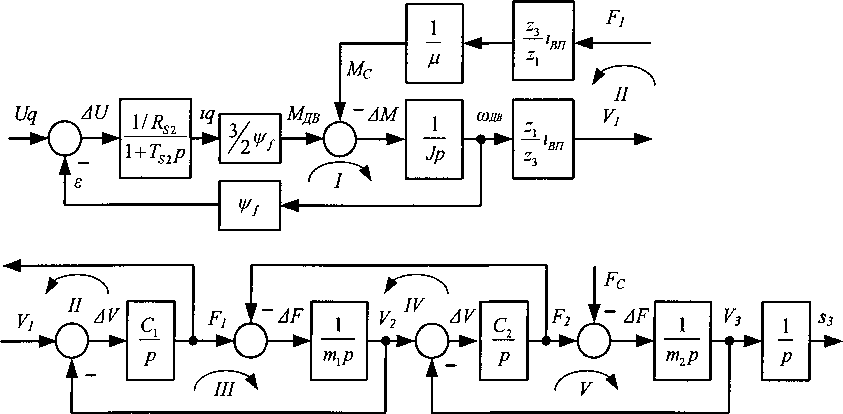
Рис. 2. Исходная структурная схема ЭМС

Декомпозиция электромеханической системы механизма подачи трубы стана ХПТ-450

Контур III, образованный упругостью и массой винта, описывает движение одномассовой упругой механической системы, которая получается, если конец винта со стороны двигателя жестко зафиксировать. При этом в контуре наблюдаются колебания с частотой VQ/^i > которые в реальности затухают из-за неизбежных потерь энергии в силовых элементах.

Контуры IV и V, образованные упругостями винта, трубы и их сосредоточенными массами, также описываются одномассовыми упругими механическими системами.

Поскольку частоты резонанса близки к частотам среза, при рассмотрении контуров как разомкнутых систем будем их считать таковыми.

Диапазоны частот среза локальных контуров, в зависимости от типа электродвигателя, указаны в таблице. На рис. 3 показаны зависимости частоты среза контура I от типа, модели и мощности электродвигателя.

Частоты среза контуров Ш, IV и V не зависят от электродвигателя и определяются исключительно параметрами механизма.

Из таблицы и рис. 3 можно сделать предварительный вывод о том, что наибольшим быстродействием обладают асинхронные электродвигатели серии RA. Эти двигатели имеют на сегодняшний день наиболее совершенную конструкцию, поэтому их показатели лучше, чем у двигателей других серий, в том числе, широко распространенной серии 4А.

Частоты среза контуров I и II в синхронном приводе, примененном ВНИИэлектроприводом, оказались наименьшими. Это говорит о не вполне удачном выборе оборудования.

Также из таблицы следует, что частота среза контура трубы V значительно превышает границу диапазона частот электропривода [5], поэтому при дальнейшем исследовании упругие свойства трубы не учитываются, и она заменяется элементом с бесконечно большой жесткостью. В результате преобразований получено, что при бесконечно большой жесткости трубы, массу трубы можно

Диапазоны частот локальных контуров

Тип двигателя	Частота среза локального контура, рад/с
	I	Z7	III	IV	V
Синхронный	5...25	50...70	120	70...400	500...1000
Постоянного тока	10...30	40...70
Асинхронный	20...40	50...80

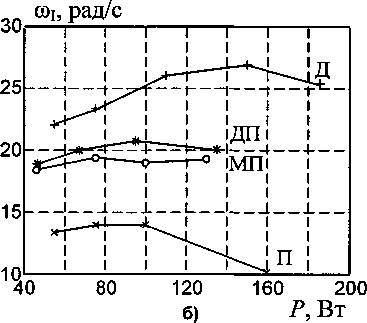
(оь рад/с

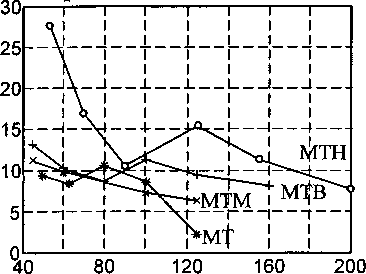
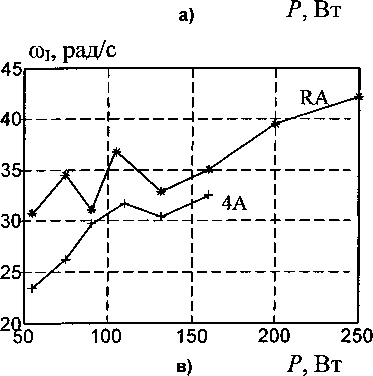
Рис. 3. Зависимость частоты среза контура / от мощности двигателя для различных серий двигателей: а) синхронный двигатель;

• б)    двигатель постоянного тока;

• в)    асинхронный двигатель

объединить с массой винтов, а силу сопротивления F_c приложить к винтам. Таким образом, из структурной схемы исключаются контуры IV и V.

№^ оценки влияния других звеньев системы построим асимптотическую частотную характеристику замкнутой системы (рис. 4). Асимптотическая ЛАЧХ L получается аппроксимацией нижних участков кривых ЛАЧХ L_n звеньев, включенных в прямой канал, и обратной ЛАЧХ -£_Ос канала обратной связи.

Из графика асимптотической ЛАЧХ видно, что канал обратной связи (электромеханическая связь) оказывает незначительное влияние на частотную характеристику замкнутой системы. Следовательно, электромеханическую связь можно исключить из структурной схемы.

Полученная ЛАЧХ соответствует характеристике «тяжелого» двигателя, когда частота среза контура / двигателя со j меньше частоты резонанса упругой механической системы <о2 ® этом случае условия для настройки регуляторов самые неблагоприятные из-за совместного влияния электромеханической инерции электродвигателя и колебательной механической системы [6].

На последнем этапе произведем нормирование структуры по общепринятой методике [1].

Величины угловых и линейных скоростей в ЭМС, величины моментов и усилий, частота и амплитуда токов и напряжений соответствуют номинальному режиму работы двигателя.

Полученная структурная схема (рис. 5) содержит только интегрирующие звенья. Физический смысл постоянных времени однотипен: постоянная времени каждого интегратора есть время, за которое выходная переменная каждого из звеньев изменяется от нуля до базового значения, если на входе этого звена действует неизменная во времени входная переменная, равная базовому значению. Например, звено с постоянной времени Т₂ изменяет скорость У_х от нуля до базового значения за время Т^ при постоянном М дв, равном М^.

Заключение

Таким образом, в результате применения метода декомпозиции ЭМС к модели механизма подачи трубы стана ХПТ-450 были получены следующие результаты.

• 1.    Влияние процессов упругой деформации трубы на работу системы признано незначительным. Математическая модель упрощена за счет замены упругости трубы элементом с бесконечно большой жесткостью.

  
  
  
  

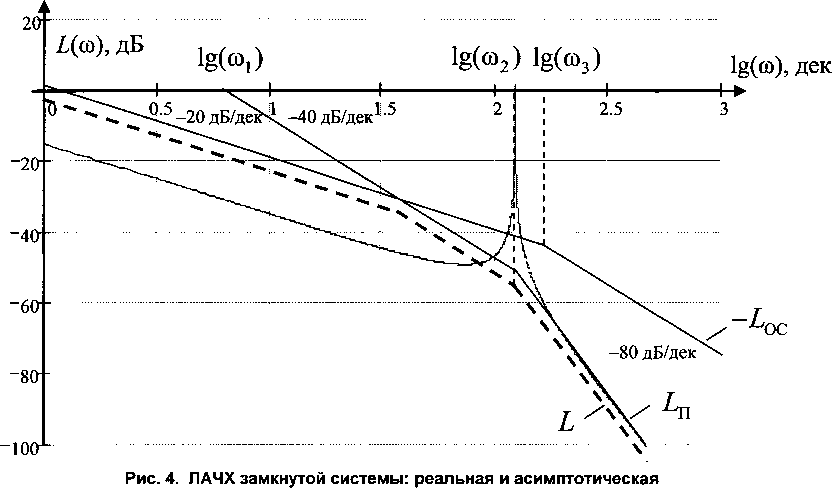
  Рис. 5. Нормированная структурная схема

  
  

• 2.    Выявлено значительное влияние электромеханической постоянной времени двигателя в существующем механизме ВНИИэлектропривода. На аналогичных механизмах можно применять двигатели с улучшенными динамическими характеристиками серии RA. Это позволит увеличить частоту среза контура саморегулирования ЭДС с 10 до 40 рад/с.

Декомпозиция электромеханической системы механизма подачи трубы стана ХПТ-450

Рассмотренный метод декомпозиции применим для широкого класса ЭМС, и позволяет эффективно исследовать влияние конструктивных параметров на работу системы посредством анализа частотных характеристик.