Декомпозиция многотемповых моделей управляемых и наблюдаемых систем

В связи с интенсивным развитием авиации, химической промышленности, нелинейной механики и других областей науки и техники возникла потребность в использовании математических моделей высокой размерности, описываемых системами дифференциальных уравнений, которые естественным образом возникают при моделировании и анализе объектов различной природы, способных одновременно совершать быстрые и медленные движения. В теории автоматического управления модели, описываемые системами сингулярно возмущенных уравнений возникают практически всегда. Примерами могут служить гироскопические, электромеханические и другие системы.

Данная работа посвящена изучению свойств управляемости и наблюдаемости сингулярно возмущенной системы. Исследование производится на основе метода декомпозиции математических моделей, отображающих свойства систем. Декомпозиция является одним из основных приемов для изучения сложных систем и состоит в расщеплении исходной задачи на ряд независимых задач меньшей размерности. Декомпозиция сингулярно возмущенных систем подразумевает частотное разделение движений на быстрые и медленные.

Цель работы:

. Понижение размерности задачи управляемости и наблюдаемости многотемповой системы, линейной по быстрым переменным так, чтобы модель меньшей размерности с большой степенью точности отражала все свойства исходной системы.

. Получение достаточных условий управляемости и наблюдаемости сингулярно возмущенных систем.

РАСЩЕПЛЯЮЩЕЕ ПРЕОБРАЗОВАНИЕ

Рассмотрим модель многотемповой систе- мы вида:

Пк=О £к^ = Л(х0'£1.....£п) +

^"=1 Aj(*0'^£1..... ^Xj + ^Bi(^O'^£P •-

£n)u, i = 0, n,                            (1)

W = ф(х0,£р ...,£„) + S"=iai;-(^£V — Е>р где xt e Xt C R"i – переменные состояния, соответствующие различным темпам движения, -X 0 – медленная переменная, ^n – самая быстрая переменная, u E I/ c r – управляющие воздействия, w E l' с Г – измеряемая координата, ft e W\i = о,п,ф e K₽ – векторные функции, V^U – матричные функции соответствующих размерностей, i = O,n,j = l,n; г, – малые положительные параметры,Et e (0,Ег°]Д = 1,71,Eq =l,tER.

Пусть для системы (1) выполняются условия [1]: 1) Собственные значения

^-i =^-iMi = 1^ матрицыД„„(хо,О, ...,0)

удовлетворяют неравенству Re 2_t< -2/?_T< 0

2) Собственные значения

А, = А,(х₀), i = l,n„_i матрицы Ai-Ln-l^O'^ '"'^ удовлетворяют неравенству Де A_t< -2P₂ < 0.

n)         Собственные         значения

Л, = Я^х0), i = 1,пг матрицы -^ii (XO'®' — '0) удовлетворяют неравенствуДе^<-2/?„<0. n+1) Функции fv Atj, i,j = O?n, Л^(хо,О,...,О), ^n-Xn-i(x0'^ —,O), — ,^ii (^0'0, —,0)

имеют достаточное число равномерно непрерывных и ограниченных частных производных по всем переменным при e_t E (o,£?],t E IR.

Используя метод декомпозиции [2] и асимптотические разложения медленных интегральных многообразий [3], произведем гладкую замену переменных:

*0 = ^V0 + 5у=1 Щ = 1 ^£к^В0 »^Xi ^{= V}i + ^i

ХП = Vn +hn.

где К, = МЛс- ..Д-нЛ;, .:,fj,

Hq = Н^(у₀,Г₁,Е₁,...,Е_п)Л₁ = ^(Vg

+^£1#0'^£1..... ^Еп).Н^ = Я2(р_о + Ех^

V1 + hpV₂,£p ...,е„)Л₂ = h₂(v₀ + в_г X Hq + £₁Е₂Яд,Р₁ + fq 4- E₂H^,E_v .... £„),< = ОД; н* = #/(v₀ +Eg IR=i=t ^6- V, + ^ + ^1=2 ПД2 ^ek^V —' ^Vj-X + hj__v VpE_v ..., £„),; = 3~n, i = 0,7 - 1;

^hi = M^vo + 3=1 Пк=1 ^£k^o^i + ^ki

-^П^И, /_.-<__-.

X f^-pEp ...,£„), i = 3,n — 1.

W = ф1(у0,и1,...,Гп,Е1,...,Еп).

Здесь

A^^O + E^o^Ep ...,£„) = Л1:1(ГО + e^q.e^ ...,£„) -Е1—^уЛ01(р0 + 9^d

^£i#o'^£i.....^£_пЬу₀^{(1) =v}o +^£i#o;

^it(V0 + 5}=1 Пк=1 Ek//g , E1; ...,£„) =

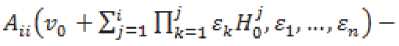
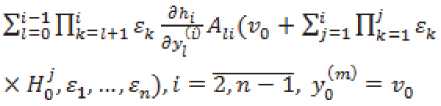
+ 5y=iIIk=1£k^o' m ~ ^n ^'

После такой замены получим систему «блоч но-треугольного» вида:

”() = /об^Р - ' ^Еп) + ^Л01 Of)' ^£Р - ^En>l<^VQ, ^£1.....^£п) + ^Л02 Оо' ^£1.....^£п)

X k2(v0, ^(Vg, Ер ...,£„), Ер ..., £„) + - + ^O.n-l^O' £Р — £п)^п-1Ь ^1О(Р

E_V ....Е^Лг^оЛх^о, Ер -,Е„), Ер

*^Е_гН^ кр h₂..... h_n__v E_t..... £„)) +

B^(v₀, Е^Н^..... П^! Е_кН",_Е1E^U.

Ш = 1 Е_ки; — Л „ (Vg, E^q, .... Щ=1 Е_кЯд, ^£1.....^£n)^Vi + А^О' ^£1^Н0.....IIU1 Е_к^0' х Hq, E_v .... £„)(/l_n(v₀ + 5}=1 Щ₌₁ Ek^o >

V! + h₁ + S}=2 П_к=2 Ek^v —»^ri + ^i' ^i+1' ..., h_n-l,Ep ...,£„) — h.„(v₀ + Sj = i П_к=1 E_k X Hq, Vi + h_t + Z}=2 n{₌₂ ^Ek^v —>\,

У1^(р) = 171 + Hi(v₀ + Ei//p£p ...,£„) + 4=2 Пк=2 ^Ek ^HvP = 2,n - 1,7^ =

Vq-X + hq-x + EqH^.q = 2,71;

B^ (v₀, E_tH^..... Пк= i E_kH^ , Ex..... £„)

⁼ ®n (^V0 + S/=l Щ₌₁ Ek^o , Ex» —» £_n)

5"=o¹ 2k=z+i E_k ^ B_t (v₀ + 4=1 Пк=1 ^Ek

X H^JQ, Ex..... £„), S, (v₀, ExH^,..., n;₌₁ E_k

X ^O'£P ...» £n) = ®i(V0 + 5у=1Пк=1£к

■ ^HQ' ^£v —' ^£n) ^— ^" ^Bn (^V0 + 4=1 Пк=1 ^Ek

X H^, Ex,..., £„), i = 0,71-1; Фх = Ф(у_о,

^£1.....^£n) + 5k=i a_ik Oo' ^£1.....^£_n)Ok +

^k + 5"=к+1Пр=к+1 ^EpH_k,k = l,n — 1.

Функции ■': л можно искать как асимптотические разложения:

^1(у₀⁽¹⁾,^£1...... ^Еп ) = Sk>0 ^£i^k/lik(y₀⁽¹⁾'

• ^Е2.....^ЕпУ» ^ki^.....Yi-X»^E1.....^Еп)

= 5к>оА» (y0G).....Унг £1.....£i-v

£i+P -»£„); ^(v0,Vp Ер ...,£„) =

5к>0^£1^0к С^О^Р^' —»^Еп)» ^/(Уо^

...У^ЗрУрЕр ...,£„) = Lk>04Hik^

-, Уу-р Vj,Ер ..., Ej-p Ej+p ..., £„), i = O,j- 1, из соответствующих уравнений:

^е1-гЙт(№о + £i#^£p -*^£„) +

2^=1 ^Л0/ (v₀ + E^.Ep ....E^hj^Q +

2^₌₁Пк=1^£к^0' ^V1 + ^1 + 2^₌₂ Пк=2 ^£k X Hp ...,V_j_₁ + /1^_₁ + E_j_₁Hj_₁,Ep ....

^En) + ^Л0п Oo + ^£l#0*^£l* -.^En)h_n(v₀ +

^Е1НоЛр h₂, .... h_n__v Ep ...,£„) = ^(Vq +^£1^O*^£V — > ^£n) + 27=1 Ду (Vq + ^£1^0 ^£V ...,£„)^(у₀ + S^^Ul^O'Vl +

• >4 + S^IlUz ^Ek^Hl.....^__г + h^ + Sj-lH^Ei......E^ + Л_1П(Р_О + E^.Ep ..., £„)/l„(v₀ + E^H^.Kp h₂, .... h_n__v Ep

Sj=onk=i+i£k^nr[/!(vo + ^}=1Пк=1£к

X Hg, e_v .... e„) + 27=i A; (^vo +

E}=1 Щ=1^£к HyEp ...,£„)/l_;(v₀ +

2ч=1Пк=1^£к^О'^V1 + ^1 + 2j₌2 Пк=2^£к X Яр ...,V_J_₁ + fl^_₁ + Ej-iHj_₁,E₁, ....

^En) + ^ZnC^O + S/=l Пк₌₁ Sk^Q . ^£1, —, ^£n) ^n(^V0 + 5у"=1Пк₌1^£1гНо.,171 + h₁ +

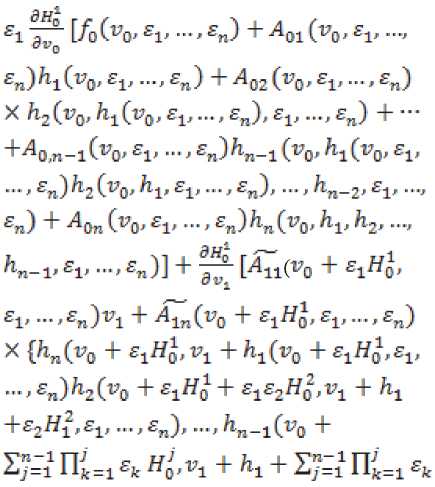
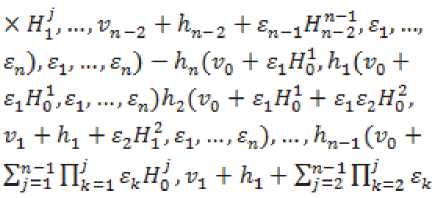
X H¹., .... V_n_₂ + h_n_₂ + ^£n-l^Hn-Z' ^£1' ■■■ ^£n).^£V -*^£_n)} = №0 + ^£1^0*^£P •* ^£n) - №0. ^£1.....^£n) + 27=1 [^Ло; Oo +

Е_гН^ £p ...,£„) ~ До/Ро,^, ...,£„)] x /t_;(v₀ +2i_=inL=i^£k^//o'^vi + ^1 + 2*1=2 Пк=2 ^£k^l' —' ^rj-l + ^/-1 + ^£j-l XHj__v £_v ...,E_n),

^₌₂ 11^=2 ^Ek^Hl.".Vj-x + Kj^ + Ej^ ^{X Д}/-Р ^hj.-, Vp ^£1.....^£n)l = fi Oo +

S}=1 Щ₌₁^£k^0 '^£v — ' ^£n) "*" S7=l ^ij (^v0 + 2}=1 Пк=1 ^£k^o ^,£v ■"^,

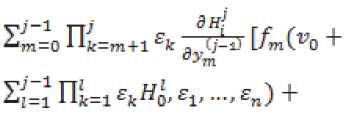
^£n)^/(^V0 + 2j₌₁Hk=l^£k^0'^V1 + ^1 + 2*1=2 Пк=2 ^Ek ^V — ' ^Vj-1 + ^/-1 + ^Ej-1 x Hj__v E_v ..., £_n) + ^„(Vq + £}=1 Щ₌₁ E_kH^ ,E_V .... £„) h„(v₀ + £}=1 Щ₌₁ E_kH^ , v_t + /4 + Sj₌₂ Пк=2 ^£k X Hp .... Vj__t + h^ + Ej-iH^, hj,.... ^hn-v^Ei> -.E_n),i = 2,n - 1.

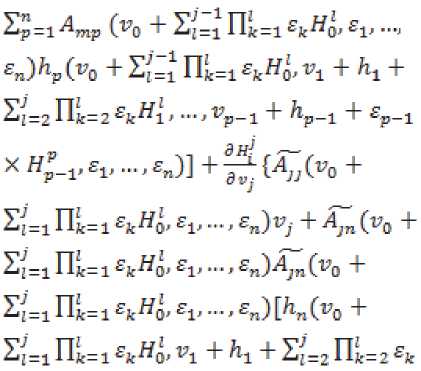
^х ^.....^ + \- ^hi+i..... ^i-p ^£i.....^£„)

-fc„(v₀+z^₌₁ nUi ^£k^H^ ^vi + ^hi + S;₌2 Пк=2 ^£k^l' — '^i’^i+V "* '^n-V⁶!' - » ^£n)l} = ft Oo + ^=1 Пк= 1 E_k H^l_Q, E_V - » ^£n) ~ fi Oo + ^=1 Пк=1 E_k Hq, £_V .... ^£n) + Sp=l[Ap(^V0 + ^z = l Пк=1 ^£k^O'^£1 ...,E_R)h_p(v₀ + ^_=inL=i ^£_k^o^i + ^hi

+Е;=2 Пк=2 £k^l' —'Vp-1 + ^p-1 + £p-l

X ^p-l»^£p ■■•»^£n) ^ipC^O + ^ Пк=1^£к ^HO-^E1.....^Еп>р^О + £;=1 Пк=1 ^£k^0' I?! + /4 + £{=2 Пк=2 ^Ek XH^,...,v_p_₁ + hp-v^£v-'^s«)]'

i = O,j- 1;

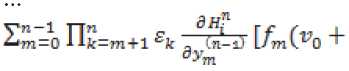
^p-l^mp l^v0 ■ ^1=1 ll^l^k^O^V^

^En>A^VO + 2?=/ Hk=l E_kH^, ^ + ^ +

^1=2 Пк=2 ^£k^l' —'^vn-l + ^-P ^CP —' ~

— ^£n>n = №o + ^1Пк=1^Ек^Но,^Е1, -. E^ - fi Oo + 2^=1 Пк=1 E_kH^, E_V .... sJ + SMApCvo + Zr=inUi^£k^ ^£P — '^£n)^p(^VO + ^=1Пк=1 ^£k^O'^Vl + ^i + £^₌₂Пк=2 ^£k^L —'^vp-i + ^p-i + ^£p-l ^Hp-V^EV-.^E^ ~^Aip(yo + £T=1 Пк=1 ^£k^0< ^eP —' ^£n)^p(^VO + 2^=1 Пк=1 Е_кН^, ^vi + ^i + Е^г¹ Пк=2 ^£k

i = 0,n — 1