Декомпозиция моделей линейных управляемых и наблюдаемых двухтемповых систем

Исследованию свойств управляемости и наблюдаемости линейных двухтемповых систем посвящено большое количество публикаций. В работах [1,2,3,4,5] исследована управляемость и наблюдаемость линейных двухтемповых систем. Асимптотическая устойчивость, управляемость, сильная и слабая управляемость линейных многотемповых автономных систем изучена в работе [6]. Управляемость некоторых линейных автономных разнотемповых систем и множества достижимости изучены в работах [7,8]. Задачи // DO–оптимального управления сингулярно возмущенной линейной системой изучены в [9]. В [10] построено асимптотическое приближение к решению задачи оптимального быстродействия для линейной автономной сингулярно возмущенной системы. Проблема управляемости и стабилизируемости линейных сингулярно возмущенных систем с запаздыванием исследовалась в [11]. Условия полной управляемости линейных автономных систем с разными степенями малого параметра при производных исследована в работе [8]. Данная работа посвящена изучению свойств управляемости и наблюдаемости двухтемповой линейной системы.

Цель работы:

. Понижение размерности задачи управляемости и наблюдаемости линейной двухтемповой системы так, чтобы модель меньшей размерности с большой степенью точности отражала все свойства исходной системы.

. Получение достаточных условий, управляемости и наблюдаемости сингулярно возмущенных систем.

РАСЩЕПЛЯЮЩЕЕ ПРЕОБРАЗОВАНИЕ

Рассмотрим математическую модель линейной двухтемповой системы:

^1 = ^11^1 + A₁₂X₂ + ^U, £±₂⁼ ^21^xl +

A₂₂x₂ + B₂u,y = C^ + C₂x₂,   (1)

где x_t e R^r" – переменные состояния, i=1,2, и e к – управляющие воздействия, y e и – измеряемая координата, Ду = ДуС^е),#, = B^t.E^.Ct =

C_t(t,£),i,j = 1,2 – матричные функции соответствующих размерностей, £ – малый положительный параметр £ e (o,£_o], *1,^2 – медленная и быстрая переменные, соответственно, t e Я точка обозначает дифференцирование по £".

Будем предполагать [12], что матрицы ^у^яг1^ 0\Bi,Ci непрерывны и ограничены вместе сдостаточным количеством производных по tи£ при t e r,£ e [o,£o] и, следовательно, имеют место асимптотические разложения: А^,е) = Ek^Ct) + ^^^(tEj^.^s) = Е^О^^Ю+ ^B^a.eXCiCts) = Eto^c^to + ^c^^s), с гладкими и ограниченными коэффициентами. Предположим, также, что собственные значе -ния Ai = Ai (t), i = 1, n2 матрицы ^22 (^ 0) удовлетворяют неравенству Re At < -pi < 0. Расщепляющее преобразование имеет вид У1 = %i - еНу2,у2 = x2- Lxtl где функции

H = H(t,e),L = L(t,E) выбираются из условия, что результирующая дифференциальная система имеет блочно–диагональный вид. Выражая пере -менные X!,X₂, произведем последовательную заме -ну переменных в исходной системе. В результате которой получим систему блочно–диагонального вида

У1 ^{= Л}1У1 + ^Bi^> ^£Уг ^{= л}2У₂ + В₂и,

(2) где

S₂ “ ^2 eL#B ^, В-^ —— S ^    В В 2,С ₃ —— С ^

Функции могут быть найдены в виде асимптотических разложений L(t,E) = y.k^QEkL(k4t),H(t,E>) = Zk>0£kW(ti(t), из матричных уравнений

Л22 + ^22^* — ^^ — ^^(Лц ~Ь Л221) ~ О,

Л₁₂ + еА₁Н — еН — НА_г = 0.

Коэффициенты в асимптотических ложениях определяются следующим

зом:

"л^,//™

(3) раз-обра-/=). ™12

диагонального вида:

Уд = —0.34y^ + y^ + o(s²),y_v = 13.534 ■ y_p - 0.305ур + и + О (е²), у_ф = У_ф + О(е²У у_з = 3273.68у_р - 90949.1у_р - ЗУОбЗВу^ -–

Еу₂ = —0.03у₂ — 0.23u + 0(£²),w = (с₂ + 15938.5с₆)у_д + (с₂ + 398.5с₆)У„ + (с₃ -368.63с₆)уф + (с₄ - 33,3бс₆)у₃+ c₅y_q

",£и =

Быстрая подсистема нулевого приближения системы (5) является управляемой и наблюдаемой. Медленная подсистема нулевого приближения системы (5) управляемая, так как ранг матрицы управляемости

.У "22

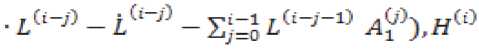
= (А® + ^zoA^^""¹¹ - Н^И -1^₀Н^и-»^^У ,i 5

О

-7.659

1    -0.65

-0.305 13.63

1   -0.305

13.85

4.57 13.627

-17.66 180.1 4.57

-353.07-214.95 -4706.33 2856.46

О о

102    —65.79/

= 5.

Л^^ = Л^¹^ + У' A^L^^-^    = Л^¹^

где

У t-l 7 (t-J-1) Д^

2-ij-O ^{L       н}12 ■

УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ

Управляемость и наблюдаемость линейных неавтономных разнотемповых систем изучена в работе [13]. Исследование управляемости и наблюдаемости линейных автономных систем производится с использованием критерия Калмана.

Пример 1. Рассмотрим модель управления центром тяжести крестокрылого снаряда в боковом движении, которая описывается линейной автономной двухтемповой системой [14]:

Р = —0.34/? + ф-,ф = 13. 534/? - 0.305^

+г1;*ф = ф; z₃ = z; z_q = —300/? + ЗООтр; ez = —10.6ф — 10^i — O.OOlz. — 0.03z — — 0.23ti — 4£²u, w = c_xP + с₂ф + с₃ф + c₄ ■

Z_B + Cg^ + C₆z, коэффициенты

(4) Произве-

дем последовательную замену переменной: y₂ = z - L%,y₁ = X - ЕНу_г,Х = (P ф ^ Z₃ Zqj.y^ =

(Уд Уф Уф y3 yqy, штрих означает транспонирование. Матричные функции                          определяют ся из матричных уравнений вида (3) (15938.5 398.5 -368.6 -33.4 0)+O(e2),

. В результате такой замены, получим систему блочно–

Медленная подсистема нулевого приближения системы (5) наблюдаемая, так как ранг матрицы наблюдаемости полный, т.е. равен 5. Значит, система (5) является управляемой и наблюдаемой. Так как блочно–диагональная система получена из системы (4) с помощью обратимой замены переменных, то данная система (4) является управляемой и наблюдаемой.

Пример 2. Рассмотрим модель системы нелинейных осцилляторов [15]:

Ex_t + а_;(х² + х² — l)x_t + b_f(l — E)x_t = a_tu, i = 1,71; ex_k + d_kx_k + sh_k(x_k + x^)

+ c_ksinx_k = P_ku,k = n+Tp; w = 2^₌₁(^x_; + SjXj),

(6) где коэффициенты отличны от нуля,           . Обозначим,

Тогда система примет вид:

k = n + l,p; w = y^^YjXj + 6^).

Линеаризуем систему вдоль

Линейное приближение системы имеет вид:

Xi = y_px_k = y_k, £y, = b^E - l)x_£ + a_ty_t +a_t-u., sy_k = (-c_k -_M)x_k - d_ky_k + P_k-u, d_k > 0, a, < 0, i = l,n; k = n + l,p; w = X^ (у^- + 5,y.).

Произведем последовательную замену пе- ременных: , b( . bi (bi \ y, =zf + —x£ + e —1-7 - 1 X£

1           °1         “i V*,      /

+ OTe2^v                 +

J,y_k Z_k x_k I "k ' ₂p_k ^dk ^dk \ ^dk/ +O(s²),x_; = v-,i = l,n; к = n + l,p;j = l,p

В результате такой замены получаем систему блочно–диагонального вида:

v_t = -v_t --u + OUJ^ = -jM T*

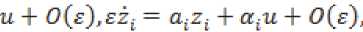
cz_k = —d_kz_k + P_ku + 0 (s),   (8)

W = Ч=_г(У^ + 5jZj) + Z”₌₁^ V_t -^-^k=n+i?^vk + °(^£)^ ⁼ Vn;^{k = n} + ^p-

Система (8) является управляемой, если у Ф---,Vi,k" i— l,n; к = n -\- l,p; и являет- “к 4

i               ci ck I bi ся наблюдаемой, если У£ +  У к — у

^L Q£ ^a ujv Q^ Q^

не равны нулю одновременно для VI, k:i = l,n; к = n + l,p. Так как система (8) получена из системы (7) с помощью обратимой замены переменной, то система (7), которая является линейным приближением данной системы (6), является управляемой и наблюдаемой при выполнении этих условий. Следовательно, система (6) является управляемой и наблюдаемой по теореме об управляемости и наблюдаемости динамических систем по линейному приближению.

Пример 3. В качестве простого примера управляемой и наблюдаемой системы, рассмотрим модель системы n кривошипно–шатунных механизмов, которая описывается линейной двухтемповой неавтономной системой [16]: ex, + (a_£ + b_t cos 2nt)x_t = c_tu, i = l,n; w=^₌₁h_kx_k, где коэффициенты a_t,b_t, Ci,hi,i = l,n отличны от нуля. Обозначим

y( =x£. Система примет вид:

x_£ = y_£,sy_£ = — (a_£ + bi cos 27rt)x_£ + c_tu, i = l,n;w = Zk=i h_kx_k. Используя критерий управляемости и наблюдаемости, получаем, что система является управляемой и наблюдаемой на отрезке [to, tj .

ЗАКЛЮЧЕНИЕ

В настоящей работе проведено исследование моделей систем, описываемых сингулярно возмущенными системами дифференциальных уравнений и изучены свойства управляемости и наблюдаемости. Проведена декомпозиция моделей управляемых и наблюдаемых линейных неавтономных двухтемповых систем. Изучены свойства управляемости и наблюдаемости автономной двухтемповой модели крестокрылого снаряда и модели системы маятникового типа.

Автор выражает глубокую признательность профессору В.А. Соболеву за полезные обсуждения и ценные советы.