Декомпозиция моделей управляемых и наблюдаемых двухтемповых систем

Исследованию свойств управляемости, наблюдаемости и стабилизируемости разнотемповых систем, линейных по быстрым переменным посвящено большое количество публикаций. Задача оптимального быстродействия двухтемповых систем изучена в работе [1], задача терминального управления с подвижным правым концом траектории изучена в [2]. В монографии [3] проведено исследование двухтемповых нелинейных автономных систем. В работе [4] для определенных значений параметра при условии ограниченных управлений построены глобальные аттракторы, в случае отсутствия ограничений на управление подобные исследования проведены в работе [5]. В монографии [6] проведено расщепление разнотемповых систем, линейных по быстрым переменным, изучены свойства управляемости, наблюдаемости, устойчивости и стабили-зируемости, свойства идентифицируемости, пассивности таких систем изучены в монографии [7]. Данная работа посвящена изучению свойств управляемости и наблюдаемости двухтемповой нелинейной неавтономной системы.

Цель работы:

. Понижение размерности задачи управляемости и наблюдаемости нелинейной двухтемповой неавтономной системы так, чтобы модель меньшей размерности с большой степенью точности отражала все свойства исходной системы.

. Получение достаточных условий, управляемости и наблюдаемости сингулярно возмущенных систем.

РАСЩЕПЛЯЮЩЕЕ ПРЕОБРАЗОВАНИЕ

Рассмотрим модель сингулярно возмущенной системы вида х = f(t,x,E) + A^t.x, s)y + B^x.e^u, sy = g(t,x, e) + A2(t,x, E^y + B2(x, e^u, W = p(t,X,E) + C(t,X,E)y, (1)

где xEXc W\y EYcr^ – медленная и быстрая переменные, uEUcW – управляющие воздействия, w G V a RP – измеряемая координата, E G (O,E_o],/(t,X, e), g (t, x, e), p (t, x, s) – векторные функции, A_t = A_i(t,x,E'),B_i = B^x, E^i = 1,2; C(t, x,s) – матричные функции соответствующих размерностей, t G ^ точка обозначает дифференцирование по t ■

Пусть для системы (1) выполняются условия [8]:

• 1)         Собственные         значения

j^j ⁼ -lj(t,x),J = l,n₂ матрицы A₂(t,x, 0) удовлетворяют неравенству ReXj < -2/? < 0.

• 2)    Уравнение g(t,x, 0) + A₂(t,x, 0)y = 0 имеет изолированное решение

у = h_Q(t,x) = — Л^С^х, 0)5 (t,x, 0).

• 3)    Функции f,g,p,A₁,A₂,A₂¹(t,x, 0),B_v B₂7 C имеют достаточное число равномерно непрерывных и ограниченных частных производных по всем аргументам при всех e G (O,£_o],t G R.

Используя метод декомпозиции [6] и асимптотические разложения медленных интегральных многообразий [9], произведем гладкую замену переменных:

x(t) = v(t) + £H(t, v(t),z(t), E^H^t, V, 0, s) = 0,y(t) = z(t) + /i(t,x(t), s).

После такой замены, получаем систему блочно–треугольного вида:

v = F(t, v, е) + S/v, еН, e)u,

EZ = Л2 (t, V, еН, E^Z + В2 (и, еН, Е^и, w = р (t, v, еН, е) + C^t, v, еН, s) (z + h(t,

(2) где v, e),F(l 0, е) = О, A2(t, г, еН, е) = Д2 (t, V + еН, е) — £ у^ (t, v + еН, е)Д1(^, V + е • Н, е),Л2(^ 0,0, е) = 0, B2(v, еН, е) = B2(v +еН,е") — Sy (t,v + еН, e)B1(v + еН,е\ Вг(г,ЕН, е) = S^v + еН, е)-^ S20' еН, е), p(t, v, еН, s) = p(t, v + еН, е) + + C(t,v + еН, E^h^t, v + еН ,s),C(t,v,EH ,е)

Функцию          мож-

b(u, t) =

FltAs) + S₁(0,0,e)u

-B₂(0,0, e)u

^> = (^(0 c2(t)),c1(t) = %(t,o,o,

e) + у- (C(t, 0,0, s) (z + h(t, 0, e)), C₂ (t) = = у (p(t, 0,0, s) + C (t, 0,0, s)(z + hQt, 0,e)), p^t.u.s) =

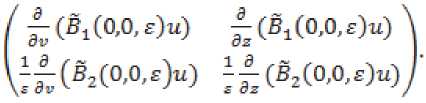
Запишем линеаризованную систему в матрич-

ном виде:

= C(t)Q) +a3(t,v,z,s).

но искать как асимптотическое разложе ние                                из урав нения h^t, х, е^ = g(t,x, е) + A2(t,x, s)h(t,x, Функцию               можно  ис-

Используя теоремы об управляемости и наблюдаемости динамических систем по линейному приближению [10], получаем условия управляемости и наблюдаемости системы (3). Так как система (1) получена из системы (3) с помощью невырожденной замены переменных, то исходная система (1) вполне управляема и вполне наблюдаема.

Пример 1. Рассмотрим модель сингулярно возмущенной системы [11]:

кать в виде асимптотического разложения из уравне-

Эн , Эн _, а , 3z ~          „ ния Ot OV              OZ х

EX, +

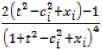
(2t + Xj) = y_eU, t = 1,71; W = Sfc= 1 h._kx_k,

e)z = F(t, v + еН,е) — F{t, v, е) + A^t, v +еН, e^z.

УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ

где коэффициенты         отличны от нуля.

Обозначим        тогда система примет вид ri = Ур ^i =             ^2t + yi) + yi“-1 = ^"i

Пусть система удовлетворяет условиям 1)–3),        . Произведем замену

Для исследования свойств управляемости и наблюдаемости блочно–треугольной системы (2), линеаризуем ее по переменным состояния вдоль

переменных:

v = — (t, 0, s) v + В_г (0,0, s)u +

y, = Zj - 2t + E

2(1 + ^^*^* 2(с^а-с^+аГ[)-1

0(s2),

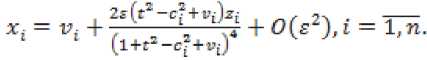
В результате получим систему блочно–треу-

a(S1(o,o,s)u)      a(S1(o,o,s)u)         ,

H--H-----^v Н--,----- z + cuCt, V, z, OV              OZ

>  ■ _ 8^2 rxcx X i З^СгАОд)*)

£ ), EZ = —— (t, 0,0, £ ) V H--=—------ v        9v v                   dz

гольного вида:

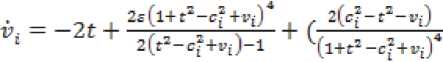
S₂(0,0, ₆)u + ^^^^^ „ + »^^_z +a₂(t,v,z,s),w = C₁(t)v + C₂(t)z+ a₃(t,v,z,fi).

Обозначим

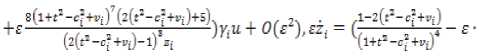
8(14C2 -с3 +уе)1(2(г"-tr- 4»f)- l)-4(14r‘ -с34«[)*) (Z^-c^rJ-l)1

^(t,0,s) ;S (--№=)

;£(^г(^ O,O,f)z)

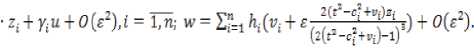
Используя теоремы об управляемости и наблюдаемости динамических систем по ли-

нейному приближению, получаем, что система блочно–треугольного вида вполне управляемая и вполне наблюдаемая, так как система нулевого приближения вполне управляемая, а система первого приближения вполне наблюдаемая. Так как система блочно–треугольного вида получена из данной с помощью обратимой замены переменных, то данная система является вполне управляемой и вполне наблюдаемой.

• Пример 2. Рассмотрим модель системы ма-

• ятникового типа с вязким трением, зависящим от времени [11]:

EXj + a,(2 + е~^с)х_е + b_t sinXj = qu, i = l,n; w = Е£₌₁/1_кх_к, где коэффициенты «А.с^ отличны от нуля. Обозначим, У_; = Xe Тогда система примет вид:

• *i = Ур^£Л = ~^bt sinXj - a, (2 + e-^yt + c_tu, i = l,n;w = 2k=i h_kx_k. Пусть система удовлетворяет условиям 1)–3), |u| < 1 . Произведем замену переменных:

  

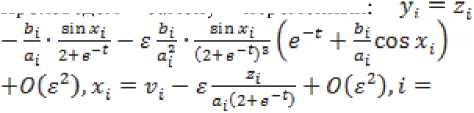
  l,n. В результате получим систему блочно–тре-

  
  

угольного вида:

^-S-^S(e'+M~^WM^^ ^ 'Sz‘+c^ i0^1=^w=2=i^ (”‘"E^)+ o(£2)'

Используя теоремы об управляемости и наблюдаемости динамических систем по линейному приближению, получаем, что система блочно–треугольного вида вполне управляемая и вполне наблюдаемая, так как система нулевого приближения вполне управляемая, а система первого приближения вполне наблюдаемая. Так как система блочно–треугольного вида получена из данной с помощью обратимой замены переменных, то данная система является вполне управляемой и вполне наблюдаемой.

ЗАКЛЮЧЕНИЕ

В настоящей работе проведено исследование моделей систем, описываемых сингулярно возмущенными системами дифференциальных уравнений и изучены свойства управляемости и наблюдаемости. Проведена декомпозиция моделей управляемых и наблюдаемых неавтономных двухтемповых систем, линейных по быстрой переменной. Изучены свойства управляемости и наблюдаемости неавтономной двухтемповой модели управления давлением системы вязкоупругих тел и системы маятникового типа с вязким трением, зависящим от времени.

Автор выражает глубокую признательность профессору В.А. Соболеву за полезные обсуждения и ценные советы.