Декрипитация эксперимента твердых ультрадисперсных фаз

Определение оптических констант веществ частиц с целью последующего их использования в вычислениях коэффициентов ослабления в некоторой мере решает проблему повышения точности расчета теплообмена излучением в энерготехнологических агрегатах.

К последнему времени опубликовано немало работ по исследованию оптических констант чистых химических соединений. Применительно к химическим составам пылей для агрегатов черной и цветной металлургии, данные по оптическим константам неизвестны.

В настоящей работе для определения оптических констант применен метод Шимона, основанный на измерении коэффициентов зеркального отражения поляризованного излучения при углах падения луча на поверхность исследуемого образца φ = 20° и 70°. Использовано состояние поляризации, при котором электрический вектор колеблется параллельно плоскости падения луча. Для реализации выбранного метода измерений принята оптическая схема спектрофотометра Спекорд М80 (рис.1.). Модулированный, с частотой 12,5 Гц, инфракрасный поток поляризуется поляризатором 2 и затем попеременно направляется качающимся зеркалом 3 в каналы измерения и сравнения кюветной камеры 4.

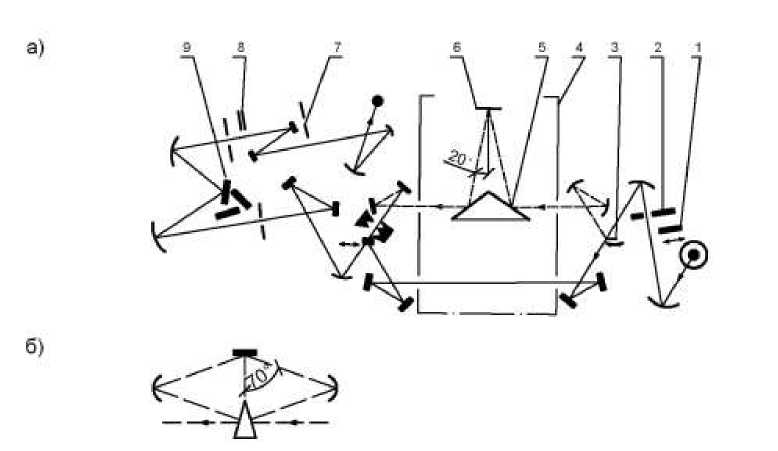
Рис.1. Оптическая схема установки для измерений спектральных коэффициентов отражения при углах 20о (а) и 70о (б)

В канале измерения при проведении экспериментов сначала устанавливается эталонное зеркало с алюминиевым покрытием, а затем – 106

исследуемый образец 6 с оптически гладкой поверхностью (рис. 8.1). Отраженный луч из кюветной камеры поступает в монохроматор, в котором системой плоских и сферических зеркал направляется через оптическую входную щель на дифракционную решетку 9 и после нее выводится через светофильтры 7, 8 на вакуумный термоэлемент с линзой из йодистого цезия. Сигнал с термоэлемента регистрируется цифровым запоминающим устройством. Коэффициент отражения от исследуемого образца определяется по формуле:

R = К э (1/1 э ),                                       (1)

где  Кэ - коэффициент отражения эталонного алюминиевого покрытия, равный 97 % ,

• 1,1_э - интенсивности отраженного излучения от образца и эталона.

Значения коэффициентов отражения выводятся на цифровое печатающее устройство с шагом Ли = 4 см-1.

Образцы были спрессованы по способу диаметром 15 мм или размером 15×15 мм толщиной от 2 до 3 мм. Различие в параметрах шероховатости отражающих поверхностей эталонного зеркала с алюминиевым покрытием и исследуемыми образцами не превышало 0,5 %.

Способ подготовки образцов явился основой для выбора метода определения оптических констант.

В методе Кравца, который также мог быть использован, проводятся измерения коэффициента отражения при нормальном падении луча один раз от поверхности образца в воздухе, второй - в специально подобранной иммерсионной жидкости. Основное требование метода - наличие оптического контакта между поверхностью образца и жидкостью, нейтральной по отношению к образцу и прозрачной во всем интервале длин волн при измерениях. Поскольку спрессованные образцы обладают гигроскопичностью, применить метод Кравца не удалось.

Определение показателя преломления n и поглощения æ по измеренным коэффициентам отражения R для двух углов φ проводилось по формулам Френеля:

RТ = (а2 +b2–2а∙соsφ+соs2φ)/ (а2 +b2+2а∙соsφ+соs2φ),(2)

RII= RТ(а2 +b2–2а∙sinφ∙tgφ+sin2φ∙tg2φ)/(а2 +b2+2а∙sinφ tgφ+sin2φ∙tg2φ)(3)

где а2 +b2 = [(n2 –æ2– sin2φ)2+4n2æ2]0,5 ,(4)

а = [0,5 [(n2 –æ2– sin2φ+((n2 –æ2– sin2φ)2+4n2æ2]0,5]] 0,5     .(5)

Здесь R Т , R II – коэффициенты отражения падающего излучения для двух поляризаций.

Как уже отмечено выше, использовано состояние поляризации падающего излучения, при котором электрический вектор колеблется параллельно плоскости падения, и задача определения оптических констант сводится к использованию двух уравнений:

R II1 = f (φ 1 , n , æ); R II2 =f(φ 1 , n , æ) .                        (6)

Для удобства работы по формулам Френеля произведен расчет на ЭВМ значений показателей преломления n и поглощения æ при изменении коэффициентов отражения с шагом ∆ R = 0,005 %. Табулирование значений с таким шагом по ∆R позволило повысить точность определения n и æ.