Демон Андреева, двигатель Андреева, цикл Андреева

В 1867 году английский физик Д.К. Максвелл придумал мысленный эксперимент с мифическими демонами с целью проиллюстрировать кажущийся парадокс второго начала термодинамики. В 1929 году Л. Сцилард предложил вариант двигателя с одной молекулой, который как бы мог нарушить второе начало. В «Феймановских лекциях по физике» Р.Ф. Фейнманом также был предложен вариант двигателя в виде вертушки с храповиком и собачкой, как вариант устройства, как бы нарушающего второе начало. Но все эти предложенные варианты так и не были созданы в виде реальных устройств. В данной статье рассматривается устройство - демон Андреева. Это устройство является полным аналогом множества демонов Максвеллы. То есть, это устройство пропускает отдельные молекулы газа с одной стороны стенки и не пропускает с другой. И конструкция этого устройства настолько проста, что его несложно изготовить в наше время. В результате появиться реальная возможность подтвердить или опровергнуть второе начало термодинамики.

В 19-ом веке английский физик Максвелл придумал мифических демонов, которые могли пропускать с одной стороны перегородки «горячие» молекулы, а с другой стороны «холодные». В то время о нанотехнологиях даже и не мечтали. Поэтому особо не разбирались с этими демонами. Пропускают и пропускают. Всё равно их нельзя было сделать. Демоны Максвелла сортировали молекулы по скоростям. Но это сложная задача и для нашего времени. Поэтому упростим алгоритм работы демонов – они будут пропускать молекулы через микроскопическое отверстие только с одной стороны перегородки. Молекулы, попадающие в створ отверстия с другой стороны перегородки, демоны пропускать не будут. Попробуем более детально разобраться в этом вопросе - см. рис. 1.

Рис. 1.

Перегородка разделяет однородный газ на 2 части – A и B. Давления в обеих частях равные. В перегородке имеется отверстие с заслонкой, которой управляет демон. Когда в створ отверстия попадает молекула со стороны A, то демон сдвигает заслонку и пропускает молекулу (а). Когда молекула подлетает со стороны B, то демон не пропускает эту молекулу (б). Сила давления газа на перегородку – это удары множества молекул газа. Поэтому давление газа со стороны A уменьшится, так как пропускаемые демоном молекулы, не оказывают давление на перегородку. Давление со стороны B останется без изменений, так как все молекулы отскакивают от перегородки или заслонки.

Разместим на перегородке радом с первым отверстием ещё одно отверстие с демоном и заслонкой (в). Только демон у этого отверстия будет пропускать молекулы со стороны B и не пропускать их со стороны A. В результате сила давления газа со стороны B также уменьшится и сравняется с силой давления со стороны A. Так как давления в A и B равны, то и равное количество молекул попадает в створ отверстий. Соответственно, равное количество молекул пропускают демоны с каждой стороны. То есть, через перегородку существуют два абсолютно независимых потока одиночных молекул из A в B и из B в A.

Как пишет Сивухин Д.В. в [1, стр. 353] про эффузионные потоки в разреженном газе, если толщина стенки и размер отверстий много меньше длины свободного пробега молекул, то через такое отверстие существуют два абсолютно независимых потока молекул. Допустим, что толщина перегородки и размер отверстия много меньше длины свободного пробега молекул. Сделаем в ней ещё одно отверстие, но без демонов (г). В результате через такое отверстие также будут существовать два абсолютно независимых потока молекул из A в B и из B в A. То есть, простое микроскопическое отверстие эквивалентно двум отверстиям с демонами Максвелла.

Допустим, что мы каким-то образом можем управлять демонами. Перегородка с демонами находится в свободном газовом пространстве. В створ каждого отверстия попадает, например, по 10 молекул в единицу времени. Если демоны будут пропускать все 10 молекул с каждой стороны, то силы давления с обеих сторон будут уравновешены. Если демоны не будут пропускать эти 10 молекул с каждой стороны, то силы давления также будут уравновешены с обеих сторон. То есть, при равном количестве пропускаемых демонами молекул, силы уравновешиваются и можно считать, что оба демона как бы не работают и не пропускают молекулы через отверстия с обеих сторон. Если демон со стороны A будут пропускать 5 молекул, а демон со стороны B будет пропускать 10 молекул, то это эквивалентно тому, что на перегородку будет действовать сила давления от 5 молекул со стороны A. То есть, можно считать, что только демон со стороны B работает и пропускает 5 молекул. Демон же со стороны A совсем не открывает заслонку и не пропускает ни одной молекулы.

Но можно регулировать количество пролетающих через отверстия молекул и другим, альтернативным способом. Допустим, что мы не можем управлять демонами и демоны пропускают все молекулы, попадающие в створ отверстия с их стороны, независимо от нас. Но в этом случае мы может управлять количеством молекул, попадающих в створ отверстий. Чем меньше давление газа – тем меньше молекул ударяется в перегородку. Соответственно, меньше молекул попадает в створ отверстий. Если создать в какой-либо части глубокий вакуум, то в створ отверстий с этой стороны молекулы практически не будут попадать и для демона с этой стороны не будет работы. Аналогично происходит и в отверстии. При разнице давлений в A и B, разное количество молекул попадает в створ отверстия со сторон A и B. Поэтому разное количество молекул будет пролетать через отверстие. То есть, регулируя давление в A или B, мы можем регулировать количество пролетающих через отверстие молекул из этой части.

Как было описано выше, простое микроскопическое отверстие (г) является аналогом двух демонов Максвелла, пропускающих молекулы с противоположных сторон перегородки.

Перегородка с двумя отверстиями, заслонками которых управляют демоны.	Перегородка с одним микроскопическим отверстием
Потоки одиночных молекул из A в B и из B в A, которые пропускают демоны совершенно независимы друг от друга.	Эффузионные потоки одиночных молекул из A в B и из B в A совершенно независимы друг от друга.
Демоны пропускают равное количество молекул с каждой стороны. Равное количество молекул пролетает через отверстия с обеих сторон перегородки.	Давления в A и B равные. Эффузионные потоки из A в B и из B в A также равны. Равное количество молекул пролетает через отверстие с обеих сторон перегородки.
Из A в B демон пропускает молекул меньше, чем пропускает демон из B в A. В результате из A в B пролетает молекул меньше, чем из B в A.	Давление в части A уменьшили. Эффузионный поток из A в B уменьшился. Эффузионный поток из B в A не изменился. В результате из A в B пролетает молекул меньше, чем из B в A.
Демон из A не пропускает ни одной молекулы. Демон из B пропускает все молекулы. В результате молекулы пролетают только из B в A.	В A создали глубокий вакуум. Поэтому эффузионный поток молекул из A в B равен 0. Из B в A эффузионный поток не изменился. В результате молекулы пролетают только из B в A.

То есть, простое микроскопическое отверстие является полным аналогом двух отверстий с демонами.

Тут главное понять разницу между большим отверстием (БО) в толстой мембране и наноотверстием (НО) в наномебране -см. рис. 2.

Рис. 2.

Уже созданы графеновые мембраны с нанометровыми отверстиями [2]. Толщина мембраны 1 атом. Наноотверстие в такой мембране можно представить в виде прослойки абсолютного вакуума толщиной в 1 атом, через которую пролетают отдельные молекулы. Пролетая через эту прослойку вакуума на длине свободного пробега (красная стрелка), внутренняя молекула становится внешней молекулой. Или наоборот - внешняя молекула становится внутренней. В большом отверстии (БО), много больше длины свободного пробега молекул, это невозможно. Там нет чёткой границы, пролетая через которую на длине свободного пробега, молекула меняет свой статус. Поэтому в большом отверстии нельзя оперировать отдельными молекулами.

И самое главное. Скорость вылетающих или влетающих молекул через наноотверстия не зависит от разницы давлений. От разницы давлений зависит только количество таких молекул. Через большое отверстие проходит газодинамический поток молекул. И скорость этого потока зависит от разницы давлений. При небольшой разнице давлений скорость такого потока может быть в 10 и более раз меньше тепловой скорости молекул. От разницы давлений зависит и количество молекул в этом потоке, проходящем через большое отверстие. Эта двойная зависимость не позволит работать нижеописанному демону, если в мембране будут большие отверстия.

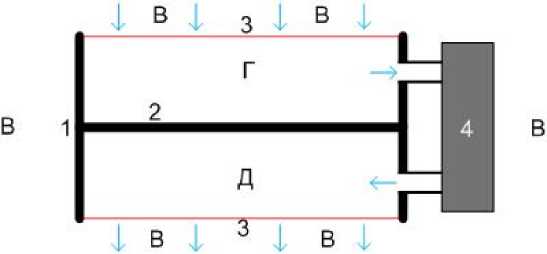
Рис. 3.

А вот конструкция устройства - демон Андреева - см. рис. 3, где 1 - сосуд. 2 – непроницаемая стенка, разделяющая сосуд на две части Г и Д. 3 - мембрана с микроскопическими отверстиями. 4 -насос. В - газовая среда вокруг сосуда. Площади и количество отверстий в обеих мембранах равны. Толщина мембран и размер отверстий в них малы по сравнению с длиной свободного пробега молекул. Это и есть демон Андреева. Как видно из рисунка, его конструкция очень проста и вполне может быть создана в современных условиях. Как же работает этот демон?

Пусть этот демон находится в разреженном газе. Предположим, что в отверстиях находятся приборы, фиксирующие разницу между эффузионными потоками молекул. Первоначально давления и температура газа внутри сосуда и снаружи равны. Эффузионные потоки: из В в Г, из Г в В, из В в Д, из Д в В – равны. Поэтому NВ = 0 и Nн = 0. Индексы в, н – это верхняя и нижняя мембраны. То есть, когда давления в частях Г, Д и В равны, то приборы зафиксируют тот факт, что между Г, Д и В нет переноса молекул. Поэтому можно считать мембраны как бы непроницаемыми. Что аналогично тому случаю, когда демоны Максвелла не работают и дверцы в отверстиях закрыты.

Включим насос 4, который будет откачивать газ из части Г в часть Д. В результате давление в части Г уменьшится относительно внешнего давления В. Так как газ из части Г откачивается в часть Д, то давление в части Д увеличится относительно внешнего давления В. Поскольку давление в Г уменьшилось, то уменьшился и эффузионный поток из Г в В. Эффузионный поток из В в Г остался неизменным, так как внешнее давление не изменилось. В результате приборы в отверстиях верхней мембраны зафиксируют разницу между влетающими и вылетающими молекулами. N ≠ 0. Результат, аналогичный показаниям приборов в отверстиях пластины, с работающими, мифическими демонами Максвелла, когда они пропускают молекулы с одной стороны.

Так как в части Д давление увеличилось, то увеличился и эффузионный поток из Д в В. Эффузионный поток из В в Д не изменился, так как внешнее давление не изменилось. В результате приборы в отверстиях нижней мембраны также зафиксируют разницу в эффузионных потоках. N ≠ 0. Результат также аналогичен показаниям приборов в отверстиях пластины с работающими демонами Максвелла. В результате работы вакуумного насоса установится динамическое равновесие. Насколько больше молекул станет влетать через верхнюю мембрану, настолько же больше молекул будет вылетать через нижнюю мембрану. Например, до включения вакуумного насоса все эффузионные потоки через каждое отверстие были равны 10 молекулам, так как давления в В, Г и Д были равны. После включения насоса потоки стали примерно такими. Из В в Г – 10

молекул, так как внешнее давление не изменилось. Из Г в В – 8 молекул, так как давление в части Г уменьшилось. NВ = 10 – 8 = 2. Из Д в В – 12 молекул, так как давление в части Д увеличилось. Из В в Д – 10 молекул, так как внешнее давление не изменилось. NН = 12 – 10 = 2. Через верхнюю мембрану в часть Г влетает 2 молекулы. Но и через нижнюю мембрану из части Д вылетает также 2 молекулы. Количество внутренних молекул внутри сосуда не изменяется. То есть, можно считать, что переноса молекул снаружи в сосуд или из сосуда наружу нет. Давления в Г и Д также будут стабильные. А если внутри демона ничего не меняется, то внутреннюю часть можно как бы убрать. Наружную поверхность верхней мембраны можно представить левой стороной пластины с демонами Максвелла. Наружную поверхность нижней мембраны можно представить правой стороной пластины с демонами Максвелла. Как если бы верхняя и нижняя мембраны сблизились и соединились в одну мембрану. Эти 2 влетевшие молекулы и 2 вылетевшие молекулы пролетают через мембраны в одном направлении. Поэтому их можно представить как 2 молекулы, которые пролетели через отверстия в пластине, дверцы которых открыли демоны Максвелла. Поэтому молекулы не оказали давление на пластину. Аналогично эти 2 влетевшие и 2 вылетевшие молекулы также не оказали воздействие на демона Андреева, как бы пролетев его насквозь. Результат аналогичен результату пластины с демонами Максвелла. И поэтому внешнее давление на демона Андреева сверху уменьшится. А давление на него снизу не изменится. Поэтому на него снизу будет действовать «демоническая» сила. То есть, демон Андреева - это полный действующий аналог множества демонов Максвелла.

Демона Андреева можно разделить на 2 части по непроницаемой стенке 2. В результате получится 2 сосуда. У каждого сосуда будет отдельный насос - см. рис. 4.

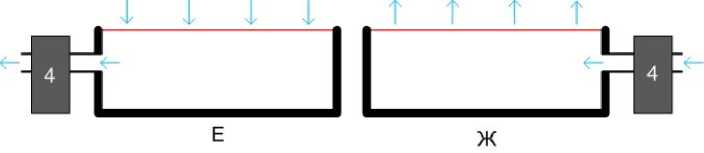
Рис. 4.

Вариант (е) эквивалентен тому варианту, когда демоны Максвелла как бы пропускают молекулы внутрь сосуда. В этом варианте вакуумный насос 4 откачивает газ из сосуда наружу и поэтому больше молекул влетает в сосуд. Вариант (ж) соответствует варианту, когда демоны Максвелла как бы пропускают молекулы из сосуда наружу. В этом варианте насос 4 закачивает внешний газ внутрь сосуда и поэтому больше молекул вылетает из сосуда через мембрану. Для чего это нужно такое разделение?

Как пишет Сивухин Д.В. [1, стр. 188], взаимодействие молекулы со стенкой можно мысленно разделить на 2 этапа. На первом этапе молекула тормозится стенкой, останавливается и как бы прилипает к стенке. При этом на стенку действует сила F1. На втором этапе молекула отталкивается стенкой, ускоряется и отскакивает от стенки. При этом на стенку действует сила F2. Эта сила подобна силе отдачи при выстреле из орудия, где роль снаряда играет отскочившая молекула. На самом деле эти 2 этапа происходят одновременно и создают результирующую силу F = F1 + F2. Но так как массы и средние скорости молекул равны, то F1 = F2 = F/2. Сосуды на рис. 4 позволяют разделить взаимодействие молекулы со стенкой на 2 отдельных этапа и разнести их в пространстве.

Рассмотрим вариант на рис. 4е. Разделим площадь стенки на 2 части. Одна часть будет равна непроницаемой части мембраны, а другая суммарной площади отверстий в мембране SО. Силы давления на непроницаемую часть мембраны и равную ей площадь стенки равны и компенсируются. Поэтому их можно не рассматривать. Для простоты понимания возьмем одно отверстие в мембране и такую же по площади часть стенки. Давление внутри и снаружи равные. Допустим, что в стенку ударяются и отскакивают 10 молекул. Соответственно и снаружи в створ отверстия будет попадать 10 молекул и влетать внутрь сосуда. Также и изнутри в створ отверстий будет попадать 10 молекул и вылетать наружу. Эти 2 потока независимы. Влетающая молекула создаёт силу F1. Вылетающая молекула создаёт силу F2. В сумме они создают силу F = F1 + F2. То есть, влетающая и вылетающая молекулы создают такую же силу, как и одна ударяющаяся и отскакивающая от стенки молекула. Поэтому 10 влетающих и 10 вылетающих через отверстие молекул компенсируют удары 10 молекул в противоположную стенку. Результат такой же, как если бы вместо отверстия была сплошная мембрана и в неё ударилось 10 внешних молекул. Насос откачивает газ из сосуда. Давление внутри понижается и вылетает 8 молекул. 8 влетающих и 8 вылетающих компенсируют 8 молекул, которые ударились в стенку. Ещё 2 влетающие молекулы можно считать как бы прилипшими к мембране. Они создают силу F = F1 + F1 и компенсируют удар в стенку ещё одной молекулы. Результат такой же, как если бы вместо отверстия была сплошная мембрана и в неё ударилось 9 внешних молекул. Уменьшив внутреннее давление, мы как бы уменьшили внешнее давление на мембрану.

С точностью до наоборот всё происходит в варианте на рис. 4ж. Первоначально через каждое отверстие влетает и вылетает по 10 молекул. Также 10 молекул ударяются в противоположную стенку. Силы компенсируются. Когда насос работает и закачивает газ в сосуд, то давление внутри увеличивается и уже 12 молекул вылетает из сосуда. 10 влетающих и 10 вылетающих молекул компенсируют 10 ударов наружных молекул в стенку. Ещё 2 вылетающие молекулы можно считать отлипшими от мембраны молекулами, которые создают силу F = F2 + F2. Две вылетевшие молекулы эквивалентны одной дополнительной внешней молекуле, которая как бы ударилась и отскочила от мембраны. Результат такой же, как если бы вместо отверстия была сплошная мембрана и в неё ударилось 11 внешних молекул. То есть, внешнее давление на мембрану как бы увеличилось. Таким образом, уменьшая или увеличивая внутреннее давление в сосуде, мы как бы уменьшаем или увеличиваем внешнее давление на мембрану.

Рассмотрим снова демона Андреева, как на рис. 3. Если при ударе и отскоке молекулы от стенки силы F1 и F2 складываются, то в случае с демоном силы вычитаются. Сила F1, от влетающей в верхнюю часть сосуда молекулы, действует на непроницаемую стенку 2 вниз. Сила F2, от вылетающей из нижней части сосуда молекулы, действует на непроницаемую стенку 2 вверх. Результирующая сила F = F1 – F2 = 0. Поэтому влетающую и вылетающую молекулы можно представить одной молекулой, которая как бы пролетела через демона Андреева насквозь и не оказала на него воздействие. С помощью мембраны мы разнесли в пространстве этапы взаимодействия молекулы со стенкой. К верхней мембране молекулы как бы прилипают, а от нижней мембраны молекулы как бы отлипают.

Если есть аналог демонов Максвелла, то можно на его основе попробовать сделать «вечный» двигатель второго рода. Это не сложно. Для начала выясним, какие силы действуют на сосуд при вылете молекул. Возьмём сосуд, как на рис. 4ж и рассмотрим силы, действующие на сосуд - см. рис. 5.

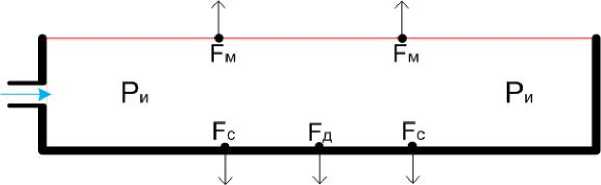
Рис. 5.

При нагнетании газа внутрь сосуда, внутри создаётся избыточное давление P_И. Это давление оказывает силу давления на мембрану и противоположную стенку. Площади мембраны и противоположной стенки равны S_М = S С . Сила давления на стенку F С = P И S С . Сила давления на мембрану F_М = P И (S_М - S О ), так как площадь мембраны, в которую ударяются молекулы, меньше общей площади мембраны на суммарную площадь отверстий в мембране. И молекулы, попадающие в отверстия, не оказывают давление на мембрану. Но так как S_М = S С , то F_М = P И (S С - S О ), Эти силы противодействуют. В результате на сосуд действует "демоническая" сила F Д = F_С - F_М = P_ИS_С - P_И(S_С - S_О) = P_ИS_О. Эта сила создаётся за счёт вылетающих молекул, которые не создали силу давления на мембрану, так как попали в отверстия и вылетели. Но как было описано выше, каждая вылетающая молекула создаёт только силу F₂ = F/2. Поэтому F Д = P_ИS_О/2.

Если же насос откачивает газ из сосуда, как на рис. 4е, то силы действуют на внешние поверхности сосуда и мембраны - см. рис. 6.

Ри Fm            Fm Р и

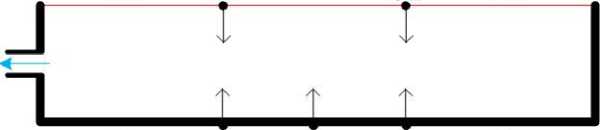
Ри Fc Fa Fc Р_и

Рис. 6.

Так как внутреннее давление меньше наружного, то можно считать наружное давление избыточным PИ. Это давление оказывает силу давления на наружные поверхности мембраны и противоположной стенки. Аналогично SМ = SС. Сила давления на стенку FС = PИSС. Сила давления на мембрану FМ = PИ(SС - SО). Эти силы противодействуют. В результате на сосуд действует «демоническая» сила FД = FС - FМ = PИSС - PИ(SС - SО) = PИSО. Но как было описано выше, каждая влетающая молекула создаёт только силу F1 =F/2. Поэтому на внешнюю поверхность стенки действует «демоническая» сила FД = PИSО/2. Эта сила возникает за счёт уменьшения внешнего давление со стороны мембраны за счёт влетающих в сосуд внешних молекул.

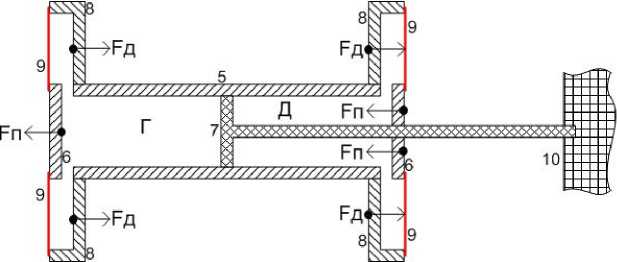
Рис. 7.

А теперь рассмотрим конструкцию двигателя на основе данного демона Андреева- см. рис. 7, где 5 - малый цилиндр. 6 -торцевые стенки малого цилиндра. 7 - поршень. 8 - большой цилиндр, коаксиально закреплённый на малом цилиндре. 9 -мембрана с микроскопическими отверстиями. 10 - опора, в которой закреплён шток поршня. Шток проходит через отверстие в правой торцевой стенке. Место прохода герметично. Внутренний объём малого цилиндра через боковые отверстия в малом цилиндре соединяется с внутренними объёмами больших цилиндров. Поршень делит малый цилиндр на две части Г и Д. Часть Г малого цилиндра и большой левый цилиндр представляют как бы часть Г демона на рис. 3. Часть Д малого цилиндра и правый большой цилиндр как бы представляют часть Д демона на рис. 3. Поршень в данном случае играет роль насоса. При движении цилиндров в какую-либо сторону, в одной части давление увеличивается, а в другой уменьшается. Как работает данный двигатель?

Допустим, что цилиндры под действием внешней силы сдвинулись вправо. В результате давление в части Г повышается, а в части Д понижается. В части Г действуют противодействующие силы FД и FП - сила, действующая на поршень. По закону Ньютона - действие равно противодействию, FП = PИSП, где SП - площадь поршня. Принцип создания силы FД рассмотрен выше на примерах с рис. 5 и 6. Чтобы двигатель заработал, необходимое условие FД > FП. FД = PИSО/2. Результирующая сила, действующая на левую часть двигателя равна FР = FД - FП = PИSО/2 - PИSП = PИ(SО/2 - SП). На правую часть действуют такая же сила, только на внешнюю поверхность большого цилиндра FР = PИ(SО/2 - SП). А суммарная сила действующая на двигатель FСУМ = PИ(SО/2 - SП) + PИ(SО/2 - SП) = PИ(SО - 2SП). Отсюда следует, что для работы двигателя необходимо условие SО > 2SП. Под действием силы FСУМ поршни продолжат движение вправо уже без участия внешней силы. При движении цилиндров влево приложения сил поменяются. Но на цилиндры также будет действовать сила FСУМ = PИ(SО - 2SП).

Сила F П = P И S П является «вредной» и её надо уменьшить. Для этого достаточно уменьшить P_И. Увеличивая S_О в 2 раза, мы уменьшаем P_И также в 2 раза, так как молекулам легче вылетать через более большую суммарную площадь отверстий. Но сила F Д = P И S О /2 останется без изменений, так как во сколько раз уменьшится P_И, то во столько же раз увеличится S_О. Увеличивая S_О, мы уменьшаем F_П. Но F Д при этом остаётся неизменной.

При рассмотрении явления вязкости газов приводится предельно упрощённый расчёт [1, стр. 336]. Применим его и здесь. Будем считать, что скорости всех молекул одинаковыми. Кроме того, при рассмотрении движения молекул будем рассуждать так, как если бы все молекулы были разделены на шесть одинаковых потоков, параллельных координатным осям. Таким образом, 1/6 часть молекул будет двигаться к мембране, 1/6 - от мембраны. Естественно, что молекулы, двигающиеся от мембраны, не могут вылететь через мембрану. Остальные 4/6 частей молекул будут двигаться параллельно мембране и также не смогут вылетать. То есть, через мембрану могут вылетать только молекулы из 1/6 части молекул, которые могут попасть в отверстия в мембране. Поэтому движение молекул через отверстия мембраны направленное, а не хаотичное.

Тут надо понять разницу между наноотверстиями и большими отверстиями в мембране. В случае с наноотверстиями через мембрану могут пролетать только 1/6 часть молекул, которые движутся к мембране. Остальные 5/6 частей молекул пролететь через мембрану не могут. В случае большого отверстия через него могут пролететь все молекулы в составе газодинамического потока молекул. В том числе и молекулы

Доклады независимых авторов 2017 выпуск 40 двигающиеся параллельно мембране, так как размер отверстия много больше длины свободного пробега молекул. Скорость этого потока равна векторной сумме скоростей всех молекул этого потока. А так как молекулы двигаются хаотично, то скорость этого потока всегда меньше тепловой скорости молекул. Поэтому и реактивная сила, создаваемая газодинамическим потоком будет всегда меньше F Д , создаваемой отдельными молекулами. Это можно сравнить с таким примером. Можно выстрелить из рогатки патроном. Скорость патрона зависит от количества затраченной нами энергии. А можно выстрелить патроном из пистолета. Скорость будет в десятки раз больше, так как используется энергия сгорания пороха. И эта скорость не зависит от наших усилий. Скорость потока зависит от разности давлений, созданного нами. Скорости же молекул не зависят от давления. Она уже есть и нам не надо тратить энергию на придание молекулам скорости 500 м/с. Достаточно создать условия для вылета отдельных молекул в нужном направлении.

Остаётся выяснить, за счёт какой энергии двигаются цилиндры. Допустим, что цилиндры двигаются вправо. Давление P_И внутри части Г повышенное. Молекулы, вылетающие из цилиндра через мембрану, создают силу F Д . Молекулы внутри цилиндров движутся со средней тепловой скоростью, как и внешние молекулы. И вылетают молекулы через мембрану с той же средней тепловой скоростью. Но так как цилиндр, из которого вылетают молекулы, движется в противоположном относительно вылета молекул направлении, то средняя скорость вылетевших молекул будет меньше средней скорости внешних молекул. То есть, вылетающие молекулы часть своей кинетической энергии отдают цилиндру. В результате температура наружного газа у внешней поверхности мембраны левого большого цилиндра уменьшается.

Давление P_И внутри части Д пониженное. Сила F Д действует на внешнюю поверхность правого большого цилиндра, так как со стороны мембраны внешнее давление уменьшилось за счёт влетающих молекул. Под действием этой силы цилиндры движутся вправо. Это аналогично случаю движения поршня в цилиндре, когда давление с одной стороны поршня выше. Расширяющийся газ, двигая поршень, совершает работу и охлаждается. Поэтому, при движении цилиндров вправо, внешний газ у наружной поверхности правого большого цилиндра также будет охлаждаться, совершая работу по перемещению цилиндров.

Этот охлаждённый в обоих случаях газ восстановит свою внутреннюю энергию за счёт тепла окружающей среды и может снова совершать работу в следующем цикле. Получился классический «вечный» двигатель, работающий только за счёт тепла окружающей среды.

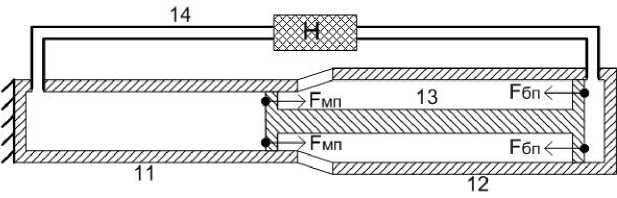
Рис. 8.

Данный двигатель можно представить как один из вариантов двигателя Стирлинга - см. рис 8, где 11 - малый цилиндр. 12 -большой цилиндр. 13 - малый и большой поршни, соединённые вместе. 14 - трубка, соединяющая внутренние объёмы малого и большого цилиндров. Н - нагреватель. Когда давления внутри и снаружи равны, то все силы компенсируются и поршни неподвижны. Начинаем нагревать нагреватель Н. Газ внутри также начинает нагреваться и создаёт внутри избыточное давление P_И. На большой поршень действует сила F_БП = P_ИS_БП. На малый поршень действует сила F_М П = P_ИS_М П . Две силы противодействуют, но поршень движется под действием более большой силы F_БП, так как S_БП > S_МП. В результате на поршни действует результирующая сила F_Р = F_БП - F_МП = P_ИS_БП - P_ИS_МП = P_И(S_Б П - S_М П ). Под действием силы F Р поршни двигаются влево. При этом вытесняемый из малого цилиндра газ, проходя через нагреватель, нагреваясь и увеличиваясь в объёме, поддерживает избыточное давление P_И внутри цилиндров. Работа по перемещению поршней происходит за счёт тепла внешнего источника. Соответственно, если газ внутри охлаждать, то внутренне давление будет уменьшаться и поршни вправо будет двигать уже внешнее давление. Для охлаждения газа также нужно затратить некоторую внешнюю энергию.

Чисто гипотетически, если бы удалось сделать так, что при движении поршней влево внутреннее давление увеличивалось, а при движении вправо – уменьшалось, то получился бы «вечный» двигатель. Но в реальности всё происходит наоборот. И вроде как невозможно сделать так, чтобы при движении поршней влево, внутреннее давление увеличивалось, а при движении вправо – уменьшалось.

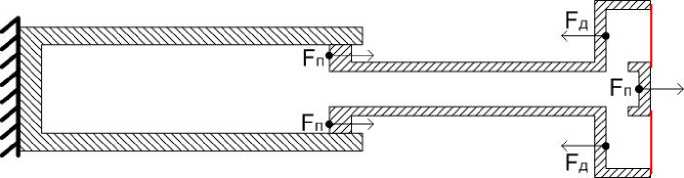
Рис. 9.

Но немного изменим конструкцию двигателя на рис. 8 - см. рис. 9. Большой цилиндр убрали. В большом поршне сделали полость, закрытую мембраной. Эта полость соединяется с объёмом малого цилиндра. Получилась половина несколько видоизменённого варианта двигателя на рис. 7. Здесь также противодействуют силы F П и F Д . Сила F П аналогична силе F МП , а сила F Д аналогична силе F_БП. Пусть S_О = 2S_БП. Тогда F Д = P_И2S_БП/2 = P_ИS_БП. Только в данном случае площадь большого поршня заменяет удвоенная суммарная площадь отверстий в мембране. F Р = F Д - F П = P И (S_Б П - S МП ). При условии S О = 2S_Б П , силы эквивалентны силам в двигателе Стирлинга на рис. 8. Но в отличие от варианта на рис. 8, при движении изменённых поршней влево, происходит увеличение внутреннего давление P_И. Вылетающие молекулы создают силу F Р , которая двигает поршни влево, поддерживая внутри избыточное давление P_И. В свою очередь P_И создаёт условия для вылета внутренних молекул через мембрану, которые создают силу F_Р. Поэтому нагрев внутреннего газа от внешнего источника в данном случае не нужен. Газ, выходящий через мембрану, охлаждается, как это было описано выше. То есть, работа по перемещению поршней производится за счёт тепла внутреннего газа.

Остаётся выяснить, каков термодинамический цикл данного двигателя. Для этого рассмотрим такой вариант двигателя - cм. рис. 10. Это половина двигателя на рис. 7. Только добавлены клапаны 15. График цикла в координатах P,V выглядит примерно так - см. рис. 11.

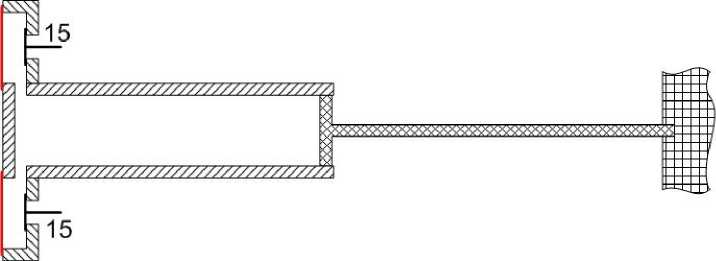
Рис. 10.

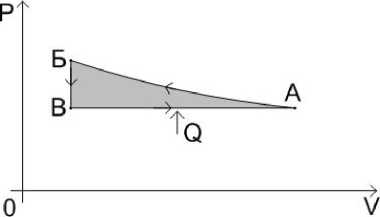
Рис. 11.

При движении цилиндров вправо, давление внутри повышается, а объём уменьшается АБ. Возникает сила F Р , которая движет цилиндры вправо до упора торца малого цилиндра в поршень. Это рабочий ход, во время которого производится какая-то работа. Выходящий через мембрану газ охлаждается, так как часть своей внутренней энергии он тратит на движение цилиндров и работу, как это было описано выше. Когда цилиндры останавливаются, то внутреннее давление сравнивается с наружным, так как молекулы газа вылетают через мембрану БВ. Затем цилиндры движутся влево и возвращаются к первоначальной точке ВА. Это холостой ход. При холостом ходе клапаны 15 открываются и внешний газ свободно поступает внутрь цилиндров. Цикл завершился. В результате внутренний газ имеет первоначальную температуру, как и до начала цикла. То есть, можно считать, что внутренний газ во время холостого хода как бы получил тепло Q от окружающей среды и восстановил свою температуру до первоначального состояния.

Аналогичный процесс происходит и при пониженном внутреннем давлении в цилиндрах - см. рис. 12. В этом случае график будет выглядеть примерно так - см. рис. 13.

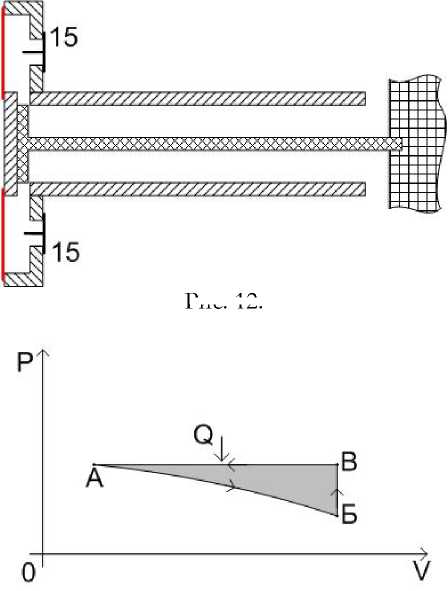
Рис. 12.

Рис. 13.

Цилиндры движутся влево.

Внутренний объём

увеличивается, а давление понижается АБ. Это рабочий ход. В данном случае движение цилиндров происходит за счёт молекул внешнего газа у наружной поверхности стенки большого цилиндра, как это было описано выше. Поэтому внешний газ у стенки охлаждается. Дойдя до крайней точки влево, цилиндры останавливаются. Внутреннее давление сравнивается с наружным БВ. Потом цилиндры движутся вправо ВА. Это холостой ход. При движении цилиндров вправо, клапаны 15 открываются и газ из цилиндра вытесняется наружу. Температура этого газа равна температуре окружающей среды. И этот газ из цилиндра вытесняет охлаждённый газ у стенки большого цилиндра. То есть, можно считать, что внешний газ у стенки восстанавливает свою температуру до первоначального состояния за счёт тепла Q, полученного от окружающей среды. Цикл завершился и система пришла в первоначальное состояние.

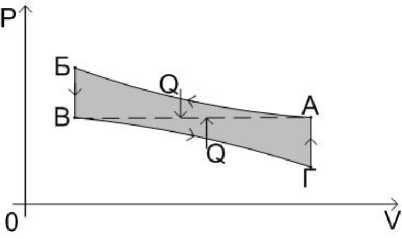
Рис. 14.

У двигателя на рис. 7 клапанов нет. Поэтому график цикла несколько иной - см. рис. 14. Этот цикл АБВГА состоит из двух совмещённых циклов АБВА и ВГАВ. Поэтому в отличие от двигателей с клапанами, здесь нет холостых ходов. Оба хода цилиндров вправо-влево являются рабочими. При движении вправо охлаждается газ со стороны мембраны. При движении влево охлаждается газ со стороны стенки большого цилиндра. Поэтому во время рабочего хода в одном месте газ охлаждается, совершая работу. Одновременно в другом месте газ получает тепло от окружающей среды, восстанавливая свою температуру до первоначальной. В цикле Карно и цикле Андреева работа совершается за счёт тепла. Только в цикле Карно рабочее тело сначала получает тепло от внешнего источника, а затем совершает полезную работу. В цикле Андреева всё происходит наоборот. Рабочее тело сначала совершает работу за счёт своего тепла. А затем рабочее тело получает тепло от окружающей среды и восстанавливает свою температуру до первоначальной. В этом случае рабочее тело ну никак не может отдать тепло окружающей среде, так как температура рабочего тела ниже температуры окружающей среды. Соответственно, холодильник в данном цикле не нужен в принципе. Кпд = 100%. Конечно, при работе такого двигателя будет происходить его нагрев за счёт трения. Но это тепло от нагрева является «топливом» для такого двигателя и поэтому оно будет повторно использовано в последующих циклах работы. Поэтому, независимо от реального кпд такого двигателя, всё тепло будет преобразовано в полезную работу.

Как уже было написано, уже есть графеновые мембраны толщиной в 1 атом и размером отверстия 1 нм [2]. Такие размеры много меньше длины свободного пробега молекул газа 70 нм при атмосферном давлении. То есть, демон Андреева и двигатель Андреева могут работать и при атмосферном давлении. И даже 86

при повышенном давлении, а не только в разреженном газе. «Демоническая» сила зависит от количества вылетевших и влетевших молекул. А это количество зависит от внутреннего объёма малого цилиндра двигателя, из которого газ вытесняется или засасывается в него. Чтобы при одинаковом внутреннем объёме количество молекул было больше, необходимо увеличивать давление газовой среды, в которой будет работать двигатель Андреева. Как это делают в двигателях Стирлинга для увеличения мощности. Для этого достаточно разместить двигатель Андреева внутри сосуда с повышенным внутренним давлением очищенного газа. Это лишний раз подтверждает родственность двигателей Андреева и Стирлинга.

Как писал А. Эйнштейн – «Воображение позволяет нам заглянуть за горизонт обыденной жизни. Воображение важнее, чем знание» . Максвелл придумал своих мифических демонов. С ними вообще ничего не понятно. Живые они или нет? Как устроены? Какую энергию используют? Сцилард придумал свой вариант «вечного» двигателя (ВД2) с двумя поршнями, перегородкой, следящей системой, памятью. Естественно, что такой сложный вариант ВД2 был неработоспособным. Фейнман придумал свой, также достаточно сложный, вариант в виде вертушки с храповиком и собачкой с пружинкой. И такой вариант ВД2 также был неработоспособен. Знаний у Максвелла, Сциларда, Фейнмана и других великих учёных было и есть очень много. Но в данном случае знания не очень важны - достаточно школьных знаний. Учёным банально не хватило воображения, чтобы придумать предложенный вариант ВД2. В этом двигателе нет ничего, что препятствовало бы работе такого ВД2. Не нарушается ни один физический закон. Если не считать второе начало термодинамики, являющееся по сути постулатом. Но пока научное сообщество в упор не хочет признавать того факта, что ВД2 возможен и даже вполне может быть изготовлен в современных условиях.

Конечно, эта статья написана не совсем научным языком. Но книга Карно «Рассуждения о движущей силе огня и машинах, способных развивать эту силу» тоже была написана не совсем научным языком. Лишь через 10 лет другой француз Э. Клапейрон придал описанию Карно канонический вид. Он ввёл все необходимые обозначения, проделал описанные словами вычисления и построил диаграммы. Так что и моё описание, я так думаю, со временем приведут к каноническому виду.