Демпфирование колебаний ротора вентильного двигателя в синхронном режиме

Постановка задачи

Система векторного управления синхронными двигателями с возбуждением от постоянных магнитов реализуется относительно просто, если имеет датчик углового положения ротора с высокой разрешающей способностью. Однако если по конструктивным или габаритным ограничениям такой датчик отсутствует, то возможно только косвенное определение углового положения ротора по сигналам с датчиков тока и напряжения. Для этого используются достаточно сложные алгоритмы с привлечением большого объема вычислительных ресурсов [1, 2]. Между тем, в некоторых случаях, когда момент сопротивления на валу двигателя изменяется незначительно, можно использовать упрощенный вид векторного управления – так называемый управляемый синхронный режим работы [3]. При реализации такого режима на статорную обмотку двигателя подается трехфазное синусоидальное напряжение, как в классическом синхронном двигателе. Это обеспечивает плавное вращение вектора поля статора. Для того чтобы ротор двигателя при этом не выходил из синхронного режима, используются сигналы с дискретного датчика положения ротора (ДПР), например, на основе датчиков Холла, установленных в воздушном зазоре двигателя. По сигналам с дискретного ДПР осуществляется грубый контроль углового положения ротора относительно статора. Если это угловое рассогласование достигнет некоторого критического значения, меняется напряжение пи- тания двигателя так, чтобы это рассогласование приблизить к нужному значению [4]. В установившемся режиме, когда нет больших возмущений, ротор двигателя вращается со скоростью вращения поля статора. Однако, как известно, ротор синхронного двигателя склонен к колебаниям, поэтому во многих случаях для устранения этих колебаний на нем устанавливают демпфирующую обмотку. В двигателях с возбуждением от постоянных магнитов наличие такой обмотки существенно усложняет конструкцию ротора и не всегда решает проблему колебательности, кроме того, ухудшает общие динамические свойства двигателя. В настоящей статье даются теоретическое обоснование и пример конкретной реализации одного из способов демпфирования колебаний ротора двигателя с возбуждением от постоянных магнитов в синхронном режиме путем введения обратной связи (ОС) по току статора с воздействием на фазу напряжения питания.

Уточнение математической модели синхронного двигателя в режиме малых колебаний

Структурную схему вентильного двигателя (ВД) в режиме синхронного вращения получим из упрощенной математической модели двигателя, представленной в [5, 6], приняв в ней угол коммутации переменным θ =var (рис. 1).

На рис . 1 обозначено: ε₀ – заданная синхронная относительная скорость вращения ротора, где

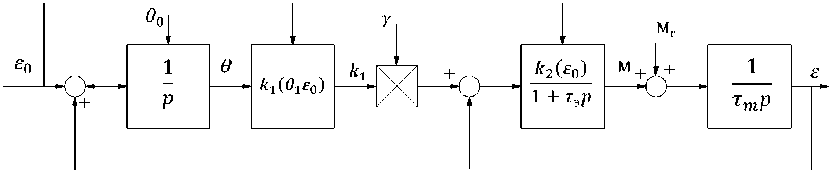
Рис. 1. Структурная схема ВД в режиме синхронного вращения

Электромеханические системы за базовое значение скорости принята скорость идеального холостого хода ω0 при θ=0; р – оператор дифференцирования; τэ = ω0L/R – относительная электромагнитная постоянная фазной обмотки; L, R – соответственно полная индуктивность и активное сопротивление фазной обмотки; τm – относительное значение электромеханической постоянной времени, равное произведению абсолютной постоянной Tm на скорость холостого хода; коэффициенты к1 (0,80) и к2 (е0) определяются по выражениям:

к 1 ( 0 , 8 ₀ ) = cos 0 + 8 _о т _эsin 0 ; (1) к 2 ( 8 0 ) = 1/ [ 1 + ( 8 о Т _э ) 2 ] . (2)

Как видно из структурной схемы, модель ВД является нелинейной как по отношению к входным воздействиям, так и к выходному сигналу. Это обстоятельство существенно затрудняет анализ динамических и статических режимов ВД. Проведем линеаризацию математической модели. Для этого применим стандартный метод линеаризации с разложением в ряд Тейлора нелинейных функций в окрестности опорной траектории и усечением до линейных членов [7]. В результате после достаточно громоздких преобразований получим линеаризованную структурную схему ВД (рис. 2).

-1 -1 y[80T3COS 0-sin 0] Тэ Т [1 + (8отэ )2 ] < [1 + (8оТэ )2 ]

В отличие от схемы на рис. 1 в данной структурной схеме учитывается возможность регулирования фазного напряжения управляющим сигналом γ. Кроме того, обозначено:

к 3 ( 0 , Y , 8 ) = y ( 8 o T ₃cos 0- sin 0 ) ; (3)

к 4 ( 8 , 0 , Y , 8 о ) =

тэ [у sin 0 - у 8отэ (2cos 0 + 8отэ sin 0) + 28о8тэ [1 + (8отэ )2 ]

0 = 9+0о.

Черточками сверху обозначены опорные значения координат, относительно которых осуществляется линеаризация.

Линеаризованная модель, представленная в пространстве состояний, может быть переписана в следующем виде (уравнения записаны в отклонениях относительно опорной траектории системы): X = Ax + Bu ;

у = Cx + Du .

Здесь помимо векторов состояния x = ( ц , 8 , 9 )^Т и входных воздействий и = ( у , 0 _о, 8 _о, ц _c )^Т введен вектор выходных переменных у = ( ц , 8 , 0 )^Т . Для матриц А , В , С и D справедливы формулы (5)–(8).

A =

В =

cos 0 + 8 _о т _э sin 0

^т э

С = о

D = о о о о

Y [8отэ cos 0 - sin б] y sin 0 - Y80тэ [2 cos 0 + 8отэ sin 0] + 28отэ8

^т э

—

m

;

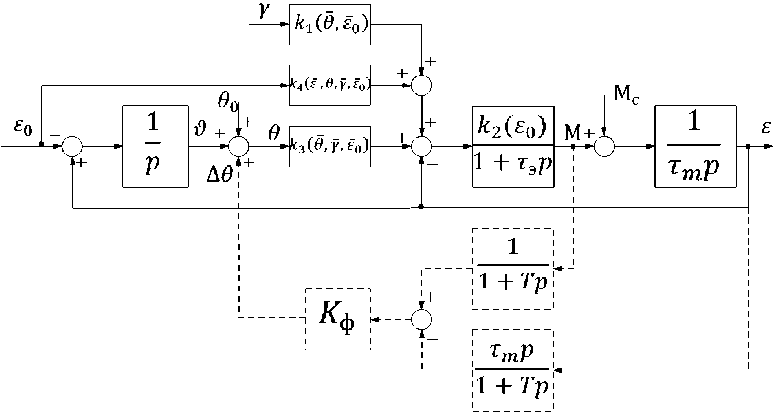
Рис. 2. Линеаризованная структурная схема ВД в режиме синхронного вращения

Изображения векторов состояния и выхода будут иметь вид:

X (p ) = ( pE - A )-1 Bu (p);

y (p) = [C(pE - A) 1B + D]u (p).

Матрица взаимосвязи между выходными переменными и входными воздействиями при нулевых начальных условиях называется матричной передаточной функцией и обозначается

W (p) = C (pE - A)-1 B + D.

Она представляет собой матрицу со следующими компонентами:

W (p ) =

W11 ( p )W21 ( p )

W 31 ( p )

W12 (p )W22 ( p )

W32 (p )

W13 (p)W23 (p )

W 33 ( p )

W14 ( p )

^W 24 ( p ) , (9)

W34 ( p )_

где W jj ( p ) = y i ( p )/ U j ( p ) - скалярные передаточ-

ные функции, связывающие две координаты. Например, W 11 ( p ) связывает электромагнитный момент двигателя ^ с управляющим сигналом 9 0 и

имеет вид

W 12 ( p ) =

ц ( p ) 9 о ( p )

____________^T m p 2 y( sin e-E 0 T ₁^cOsO)_____________

1+(Ё0Тэ )2 ](тэт mp 3 +т mp2 )+ p + Y(sin 9-ЁоТэС«5 9)

Другие передаточные функции будут отличаться только числителем, связывая другие координаты.

Матричная передаточная функция (9) может быть использована как для аналитического исследования динамических процессов, так и для синтеза корректирующих устройств. Ее анализ позволяет сформулировать различные стратегии управления вентильным приводом для всех режимов его работы. Рассмотрим одну из них.

Практическая реализация корректирующего воздействия в электроприводе

Рассмотрим синхронный режим работы ВД. Для повышения точности поддержания скорости при колебаниях нагрузки введем в закон управления составляющую, зависящую от вариации электромагнитного момента. Такая дополнительная ОС в зависимости от поддерживаемого скоростного режима и величины нагрузки должна корректировать либо амплитуду у , либо фазу 9 ₀ напряжения питания ВД. Реализуем последний вариант коррекции. Технически такая реализация достаточно проста. Информация о величине момента нагрузки двигателя может быть получена с помощью редуцированного наблюдателя [8] в соответствии с выражением

£с (p ) = W;(p )s( p)+^Л p )ц( p), где WE(p), W^( p) - корректирующие передаточные функции по соответствующим переменным. Последние могут быть выбраны в следующем виде W£ (p ) = -Tmp;

• ^E       1 + Tp

Wu (p ) = -^.

• ^ц       1 + Tp

Здесь постоянная времени Т подлежит настройке.

На основе этой информации корректирующее устройство формирует управляющий сигнал в виде фазового сдвига опорных импульсов, задающих частоту напряжения питания двигателя. Таким образом, фаза напряжения питания двигателя по сигналам корректирующего устройства может безынерционно сдвигаться вперед или назад, изменяя текущее значение угла θ. На структурной схеме (см. рис. 2) пунктирными линиями показана функциональная реализация корректирующего устройства. При этом фазосдвигающее устройство

Электромеханические системы

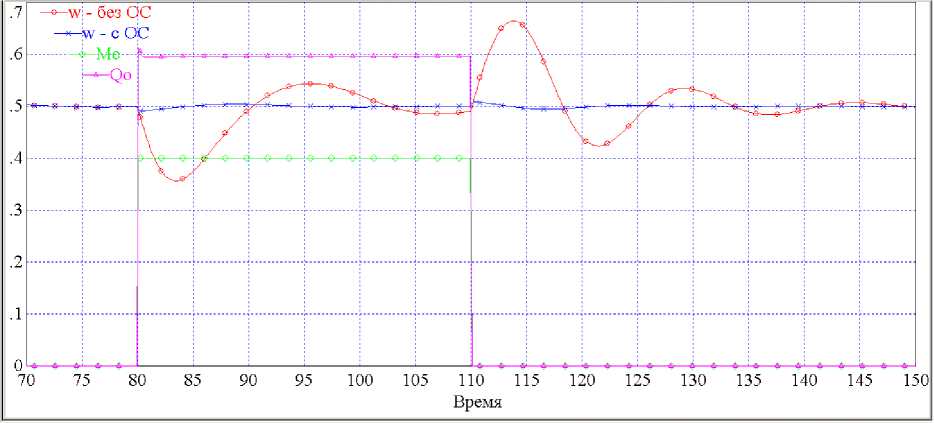
Рис. 3. Результаты моделирования работы вентильного двигателя в синхронном режиме

принято безынерционным с передаточным коэффициентом k ф . Очевидно, что изменяя вид и численные значения параметров W ( р ) мы можем влиять на динамические свойства электропривода.

На рис. 3 приведены результаты моделирования работы вентильного привода в синхронном режиме с дополнительной коррекцией. Моделирование было проведено при следующих исходных данных: у = 1; s ₀ = 0,5; т э = 0,1; т m = 5 ; T = 0,01. В момент времени t = 80 был осуществлен наброс момента нагрузки ( Ац c =+ 0,4), а в момент времени t = 110 сброс момента нагрузки ( Ац c =- 0,4). На рис. 3 представлены графики скорости е ( t ) , момента нагрузки ц c ( t ) и вариации угла коммутации 0 ₀ ( t ) .

Для наглядности на одном рис. 3 приведены две кривые скорости: одна – без введения дополнительной коррекции (без ОС), и другая – с введением в контур управления ВД корректирующей ОС по вариации момента (с ОС). Введение этой связи при изменении момента нагрузки на 0,4 ед. вызывает изменение угла коммутации примерно на 0,6 ед. Графики демонстрируют высокую эффективность такой дополнительной корректирующей обратной связи, ошибка по скорости уменьшается с 33 до 1,7 %, т. е. примерно в двадцать раз. При оптимальной настройке такой связи, которая может быть осуществлена с привлечением соответствующих компонентов матрицы (1), можно добиться практической инвариантности вентильного электропривода к вариациям момента нагрузки.