Denoising of Noisy Pixels in Video by Neighborhood Correlation Filtering Algorithm

Published Online July 2012 in MECS DOI: 10.5815/ijigsp.2012.07.07

In today’s tech-savvy world, Images and videos play a vital role. However, the image sequences are likely corrupted by noise due to bad acquisition, transmission and recording. Noise means any unwanted signal. Noise is not always random and randomness is an artificial term. Digital images, which are a subset to digital signals, are normally corrupted by many type of noise, including impulse noise and speckle noise [1]. The speckle noise disturbs the high intensity pixels into noisy. The malfunctioning pixels in camera sensors, faulty memory location in hardware, or transmission of the image in a noisy channel, are the some of the things which is made the videos and images noisy and un clarity. In the existing system that the Nonlinear filtering algorithm as well as Fuzzy algorithm has a great advantage in suppressing salt & pepper noise pollution; however, severe image blurring will occur due to the same approach to processing all the pixels blindly. Furthermore, when the sizes or density of noise spots augment, blurring degree increases[4]. As per our study the problematic area is denoising all pixels blindly without examining whether it is noise exaggerated or not. This type of proceeding loses edge information too.

Video signals are often contaminated by noise during acquisition and transmission. Denoising of video is highly desirable, which can enhance perceptual quality, increase compression effectiveness, facilitate transmission bandwidth reduction, and improve the accuracy of the subsequent feature extraction and pattern recognition processes. Most video denoising algorithms proposed in the literature consider additive white Gaussian noise and can be roughly categorized into pixel domain and transform domain methods [2]. Pixel domain denoising is usually done with weighted averaging within local 3D windows, where the weights can either be fixed or adapted based on the local image content. Improved results are obtained by applying weighted averaging after motion compensation, so that temporal correlation is taken better into account. And also the existing system has some of these demerits Existing methods, i.e.; using fuzzy tool to detect noisy pixels in each frame is computationally complex. Every time the rules are to be generated for the input sequences[1][3].

Though this kind of training is used to denoise some new input sequences, its use is restricted to denoise only impulse noise. Thus this kind of filtering methods restricts itself for denoising any particular type of noise. So that its very time consuming task and couldn’t get the preserving ability in the existing system so we are going for a better algorithm namely as the Noisy Correlation Function (NCF) algorithm which can able bring down these the disadvantages.

Section II describes the existing work of denoising using different methods. Section III details the neighborhood correlation filtering algorithm. Section IV gives the experimental results for the proposed work.

• II.    EXISTING WORK

Nonlinear filtering algorithm as well as Fuzzy algorithm has a great advantage in suppressing salt & pepper noise pollution; however, severe image blurring will occur due to the same approach to processing all the pixels blindly. Furthermore, when the sizes or density of noise spots augment, blurring degree increases. As per our study the problematic area is denoising all pixels blindly without examining whether it is noise exaggerated or not. This type of proceeding loses edge information too. Video signals are often contaminated by noise during acquisition and transmission. Denoising of video is highly desirable, which can enhance perceptual quality, increase compression effectiveness, facilitate transmission bandwidth reduction, and improve the accuracy of the subsequent feature extraction and pattern recognition processes[5].

Most video denoising algorithms proposed in the literature consider additive white Gaussian noise and can be roughly categorized into pixel domain and transform domain methods. Pixel domain denoising is usually done with weighted averaging within local 3D windows, where the weights can either be fixed or adapted based on the local image content. Improved results are obtained by applying weighted averaging after motion compensation, so that temporal correlation is taken better into account. Transform domain methods first decorrelate the video signal using a linear transform, and then denoise the signal in the transform domain (e.g., by soft/hard thresholding, maximum likelihood estimation, or Bayesian estimation), followed by an inverse transform that brings the signal back to the pixel domain[4]-[6]. Motion information or temporal correlations may be incorporated into the algorithms by employing an advanced or adapted transform or by using an advanced statistical model that reflects the joint distributions of wavelet coefficients over space and time.

Recursive filtering method has also been proposed to filter the wavelet coefficients along the estimated motion trajectories. The interest in statistical image modeling has been growing steadily in recent years. Here we are specifically interested in the Gaussian scale mixture (GSM) model, which was originally proposed in the statistics literature and has recently been applied to the modeling of static natural images [8]. Indeed, it was found to be both effective and convenient in describing the marginal and joint statistics of wavelet coefficients. Bayesian estimation method based on the GSM model has also been developed for the denoising of still images, and has achieved superior performance. But the quality of denoised sequence is degraded. Existing methods, ie; using fuzzy tool to detect noisy pixels in each frame is computationally complex. Every time the rules are to be generated for the input sequences. Though this kind of training is used to denoise some new input sequences, Its use is restricted to denoise only impulse noise. Thus this kind of filtering methods restricts itself for denoising any particular type of noise.

• III.    PROPOSED WORK

The proposal is to filter / denoise only noise exaggerated pixels. For identifying noise exaggerated pixel, we use an algorithm namely, neighborhood correlation filtering (NCF) algorithm. It has much higher edge-preserving ability by contrast; representing that even single-pixel width can be preserved in high density noise. When noise density gets higher, partial noise spots gather and form some noise blocks. Those noise blocks with big dimension cannot be entirely filtered, whatever method is used. Thus filtering noisy pixel enhances Image quality which is a major advantage of our proposal.

• A.    Correlation

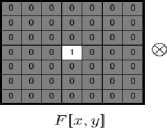
к к g^j] = ^ 5v ^fai у1^ъ+^м+v] (1) и—-к у=—к

G = H®F                  (2)

a	b	c
d	e	f
g	h	i

0	0	0	0	0	0	0
0	0	0	0	0	0	0
0	0	a	b	c	0	0
0	0	d	e		0	0
0	0	g	h	i	0	0
0	0	0	C	0	c	0
0	0	0	0	0	0	0

Figure 1. Correlation

• B.    Correlation filtering

Say the averaging window size is 2k+1 x 2k+1:

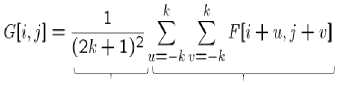
Attribute uniform weight Loop over all pixels in neighborhood around to each pixel             image pixel Ffijj

Now generalize to allow different weights depending on neighboring pixel’s relative position[9]:

к к

GKJ]= E E Я[칫иН и——к и=— к '   ¹                       (4)

Non-uniform weights

This is called cross correlation denoted,

G = H ® F (5)

Filtering an image: replace each pixel with a linear combination of its neighbors. The filter “kernel” kernel or “mask” H [ u, v ] is the prescription for the weights in the linear combination.

In the proposed system that we are going to process the filter/ denoising through the block diagram. The selected video sequences are converted to a number of frames in first step. Impulse noise and speckle noise are added to each frame in parallel[11]. In Second step each frame is subjected to color component separation.

Here we separate each frame to have three components such as R, G, B. This is an additive colour system based on tri-chromatic theory. Often found in systems that use a CRT to display images. RGB is easy to implement but non–linear with visual perception. It is device dependent and specification of colors is semi– intuitive. RGB is very common, being used in virtually every computer system as well as television, video etc. Then here from that our algorithm going to be executed through the block diagram.

A color perceived by the human eye can be defined by a linear combination of the three primary c olours red, green and blue. These three colors form the basis for the RGB colour space. Hence, each perceivable color can be defined by a vector in the threedimensional color space. The intensity is given by the length of the vector, and the actual color by the two angles describing the orientation of the vector in the color space.

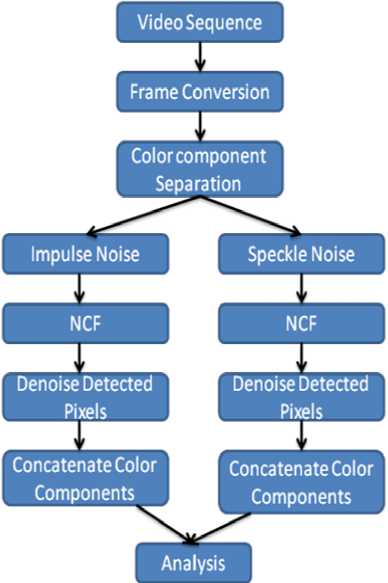
Figure 2. Block Diagram for correlation filtering

The RGB-space can also be transformed into other coordinate systems, which might be more useful for some applications. One common basis for the color space is IHS . In this coordinate system, a color is described by its intensity, hue (average wavelength) and saturation (the amount of white in the color). This color space makes it easier to directly derive the intensity and color of perceived light and is therefore more likely to be used by human beings[8]-[11].

Select a colour component frame. Let it be your original frame. Add salt & pepper noise and speckle noise separately to it. Let’s consider it as noisy frame. Do Convolution operation on your original frame. Consider it has filtered frame. We create a binary mask. This is done by creating a logical matrix. This mask is created as follows; Check the entire pixel intensity values of noisy frame. This method is convenient for selecting or adjusting parameters of the imaging system. Experiments also showed that this algorithm has certain abilities in filtering speckle noise. Owing to its simple process, high processing speed, and wide applicability for several kinds of noise, the algorithm can be used as an image pre-processing method.

Binary mask= { 1, if noisy image = 0 or 255 0 , otherwise}

Now assign, filtered frame (binary mask) to Noisy frame (binary mask). The selected frame is denoised.

The filtered separate colour components are concatenated and shown as denoised sequence[12]-[14]. To judge the performance of the proposed method, we will use the mean absolute error (MAE), the peak-signal-to-noise ratio (PSNR) and the normalized color difference (NCD) as objective measures of similarity and dissimilarity between a filtered frame and the original one, each containing rows and columns of pixels.

• IV.    EXPERIMENTAL RESULTS

To be able to judge the performance of the proposed method, we will use the mean absolute error (MAE), the peak-signal-to noise ratio (PSNR) and the normalized color difference (NCD) as objective measures of similarity and dissimilarity between a filtered frame I f (t) and the original one I o (t) , each containing m rows and n columns of pixels.

The MAE is given by мад,ад

• У^ У^У^оС^у^) - if^ ^01 (6) _ ce{R,G,2}r=ls=l

• 3 ■ n- ■ m

The lower the MAE, the more similar (less dissimilar) the images.

The PSNR value is defined as

MSE(/_O(t), I_f(t»

У2 £ i^C№, у.£) - ^(^, У’ ОТ

3 • n. • m

PSNR(l_o(t),/f(^£))                          (

= 10 ‘10610 MSE(7^W)) ’

Where S denotes the maximum possible value of a pixel component (here S =255). The higher the PSNR value, the more similar (less dissimilar) the images. Finally, the NCD, between an original and a filtered frame, is calculated as

NCD^to./Xt))

g=i s;=i H^^ У- <) " ^(^ ^ i)|| (8) ^1^11№^АВ(^У,011

Where the Euclidean norm and I o^LAB (x, y, t) and I f^LAB (x, y, t) respectively denote the L*a*b -transform [42] of the original and the filtered frame. The lower the NCD value, the more similar (less dissimilar) the images. The remainder of this section is structured as follows.

TABLE 2.Speckle Noise

	0.01	0.03	0.05	0.07	0.09	0.1
MSE	21.06	44.93	67.45	89.56	11.12	121.76
PSNR	34.89	31.60	29.84	28.60	27.67	27.27
MAE	3.86	6.64	8.54	10.10	11.44	12.04
NCD	0.07	0.084	0.096	0.106	0.115	0.12

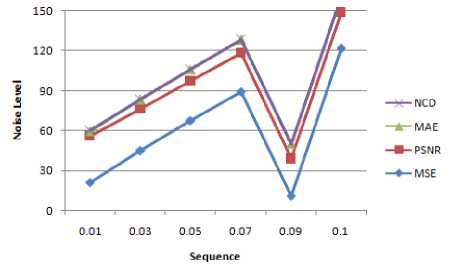
Figure 4.Speckle noise for different technique

Tabulation Results

For our project we have gone through different types of noise levels we are experiment and put it as a tabulation results for the Deadline sequence.

TABLE 1.Impulse Noise

	0.01	0.03	0.05	0.07	0.09	0.1
MSE	17.58	33.61	52.67	74.46	98.85	112.2
PSNR	35.68	32.86	30.91	29.41	28.18	27.63
MAE	0.53	1.009	1.50	2.017	2.53	2.80
NCD	0.07	0.09	0.10	0.12	0.13	0.14

(a)

(b)

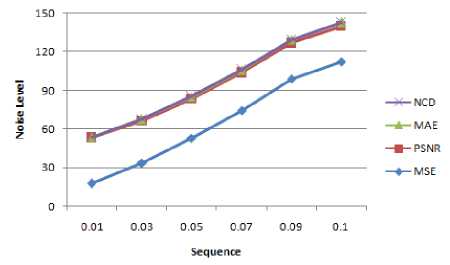
Figure 3. Impulse Noise for different technique

Figure 5. The original 40th frame of the “Table tennis” sequence (a), the frame corrupted by 20% Impulse noise (b) 30% Impulse noise (c) 40% Impulse noise respectively.

(c)

(b)

Figure 8. The original 40th frame of the “Dead line” sequence (a), the frame corrupted by 20% Speckle noise (b) 40% Speckle noise respectively.

(a)

(c)

Figure 6. The original 20th frame of the “Table tennis” sequence (a) the frame corrupted by 20% Speckle noise (b) 30% Speckle noise (c) 40% s peckle noise respectively .

Figure 7.The original 40th frame of the “Dead line” sequence, (a) the frame corrupted by 20% Impulse noise (b) 40% Impulse noise respectively.