Depth and Intensity Gabor Features Based 3D Face Recognition Using Symbolic LDA and AdaBoost

Published Online November 2013 in MECS

Face recognition using 3D information can solve some problems that occur in 2D face recognition. Due to some of the difficulties encountered in 3D face recognition, such as coping with expression variations, the inconvenience of information capture and large computational costs, these problems have been the focus of recent research .

Face recognition based on 3D information is not a new topic. Studies have been conducted since the end of the last century [1-7]. The representative methods use features extracted from the facial surface to characterize an individual. Lin et al. [8] extracted semi local summation invariant features in a rectangular region surrounding the nose of a 3D facial depth map. Then the similarity between them was computed to determine whether they belonged to the same person. Al-osaimi et al. [9] integrated local and global geometrical cues in a single compact representation for 3D face recognition. In another method, the human face is considered as a 3D surface, and the global difference between two surfaces provides the distinguishability between faces. Brumier et al.[10] constructed some central and lateral profiles to represent an individual and proposed two methods of surface matching and central/lateral profiles to compare two instances. Medioni et al.[11] built a complete and automatic system to perform face authentication by modeling 3D faces using stereo vision and analyzing the distance map between gallery and probe models. Lu et al.[12] used the hybrid iterative closest point (ICP) algorithm to align the reference model with the scanned data and adopted registration errors to distinguish between different faces. Moghaddam et al.[13] proposed a new method of bayesian matching for visual recognition. Maurer et al.[14] analyzed the performance of the GeometrixActive ID Biometric Identity system, which fused shape and texture information.

The face recognition based on combination of 3D shape information and 2D intensity/color information is a novel approach, which provides an opportunity to improve face recognition performance. In the present paper, the objective is to investigate how depth and intensity information contributes to face recognition when expression and pose variations are taken into account. Further, a robust and accurate face system is designed by selecting and fusing the most effective depth and intensity features. All the processes included in the training and test phases of the proposed approach are fully automated.

The remainder of this paper is organized as follows: the overview of the materials and methods used for this research is given in section II, and section III shows the proposed methodology. Experimental results are described in section IV. Section V concludes the research work done in this paper.

• II.    MATERIALS AND METHODS

For purpose of experimentation of the proposed methodology, the face images drawn from the following 3D face databases are considered: (i) Texas 3D face database, (ii) Boshphorus 3D face database, (iii) CASIA 3D face database

• A.    Texas 3D Face Database

  The Texas 3D Face Recognition (Texas 3DFR) database is a collection of 1149 pairs of facial color and range images of 105 adult human subjects. These images were acquired using a stereo imaging system manufactured by 3Q Technologies (Atlanta, GA) at a very high spatial resolution of 0.32 mm along the x, y, and z dimensions. During each acquisition, the color and range images were captured simultaneously and thus the two are perfectly registered to each other. This large database of two 2D and 3D facial models was acquired at the company Advanced Digital Imaging Research (ADIR), LLC (Friendswood, TX), formerly a subsidiary of Iris International, Inc. (Chatsworth, CA), with assistance from research students and faculty from the Laboratory for Image and Video Engineering (LIVE) at The University of Texas at Austin. This project was sponsored by the Advanced Technology Program of the National Institute of Standards and Technology (NIST).

Texas 3D Face Recognition Database was created to develop and test 3D face recognition algorithms intended to operate in environments with co-operative subjects, wherein, the faces are imaged in a relatively fixed position and distance from the camera [15-17].

B.    Bosphorus 3D Face Database

The Bosphorus 3D face database consists of 105 subjects in various poses, expressions and occlusion conditions. The 18 subjects have beard/moustache and the 15 subjects have hair. The majority of the subjects are aged between 25 and 35. There are 60 men and 45 women in total, and most of the subjects are Caucasian. Two types of expressions have been considered in the Bosphorus database. In the first set, the expressions are based on action units. In the second set, facial expressions corresponding to certain emotional expressions are collected. These are: happiness, surprise, fear, sadness, anger and disgust.

C.    CASIA 3D Face Database

The CASIA 3D Face Database consists of 4624 scans of 123 persons using the non-contact 3D digitizer, Minolta Vivid 910. During building the database, not only the single variations of poses, but also expressions and illuminations are considered [19].

• III.    PROPOSED METHODOLOGY

The proposed methodology employs the following: (i) Radon transform, (ii) Gabor wavelets, (iii) Symbolic LDA, (iv) Adaptive boosting algorithm (AdaBoost) classifier which are described in the following sub sections.

A.    Radon Transform

The Radon transform (RT) is a fundamental tool in many areas. The 3D Radon transform is defined using 1D projections of a 3D object f(x,y,z) where these projections are obtained by integrating f(x,y,z) on a plane, whose orientation can be described by a unit vector a . Geometrically, the continuous 3D Radon transform maps a function ³ into the set of its plane integrals in ³ . Given a 3D function f ( X ) = f ( X , y , z ) and a plane whose representation is given using the normal a and the distance s of the plane from the origin, the 3D continuous Radon Transform of f for this plane is defined by

∞∞∞

^ f ( a, s ) = J J J f ( % ) 5 ( % T a - s ) dX

-∞ -∞ -∞

∞∞∞ = ∫∫∫

-∞ -∞ -∞

f(x, y, z)δ(xsinθcosφ+ ysinθsinφ +zcosθ-s)dxdydz where X =[X, y, z]T , a = [sin 0cos ф,sin 0sin ф,cos 0]T , and 5 is

Dirac’s delta function defined by

∞

δ ( x ) = 0, x ≠ 0, ∫ δ ( x ) dx = 1 .

-∞

The Radon transform maps the spatial domain (x, y, z) to the domain ( a , S ).

B.    2D Gabor Filter

The 2D Gabor filters of depth and intensity images of faces are used to characterize an individual’s face. The

Gabor wavelets represent the properties of spatial localization, orientation selectivity, spatial frequency selectivity and quadrature phase relationships, and these have been experimentally verified to be a good approximation to the response of cortical neurons. The Gabor wavelet based representation of faces has been successfully tested in 2D face recognition. Such representation of an image describes the facial characteristics of both the spatial frequency and spatial relations. The 2D Gabor wavelets are defined as follows:

V( z ) = — exp a

k 2 z

—

2 a ²

^exP⁽ k^,v^z ) ^— exP [^— y

where z = ( x,y ) , and Ц and V define the orientation and scale of the Gabor wavelets, respectively. The wave vector k is defined as follows:

Ц , v

k . , v = k Z ^Ц

where k = k / fv and ф = пц / 8 . The constant v max J ц г kmax is the maximum frequency, and f is the spacing factor between kernels in the frequency domain. The Gabor kernels in the (3) are self-similar, since they can be generated from the mother wavelet by scaling and rotation via the wave vector k . More scales or

Ц, v rotations can increase the dependencies of neighbor samples.

In the proposed method, Gabor kernels with five different scales v g{0,...,4} and eight orientations Ц G {0,..., 7} are used, with the parameters a = 2п , and . The number of scales and max .

orientations are selected to represent the facial characteristics in terms of spatial locality and orientation selectivity. The Gabor representation of an image, called the Gabor image, is the convolution of the image with Gabor kernels as defined by (1). For each image pixel, it has two Gabor parts: the real part and imaginary part, which are transformed into two kinds of features: Gabor magnitude features and Gabor phase features. Herein, it is proposed to use the Gabor magnitude features to represent the facial features, since the Gabor transformation strongly responds to edges [20-22].

The depth Gabor images are smoother in comparison with the intensity Gabor images due to the fact that the value of the pixels in the depth image changes less than does the value in the intensity images. The smoother depth Gabor image can reduce the influence of noise, but it cannot describe the facial features in detail. This is why the face recognition is performed by combining depth and intensity information [23].

C. Symbolic LDA (S-LDA)

We consider the extension of linear discriminant analysis (LDA) to symbolic data analysis frame work [24-25].   Consider the 3D range face images

Г . Г ,..., Г , each of size M x N, from a 3D range 1, 2, , n face image database. Let Q = Г, ,Г~,...,Г be the 1, 2, , n collection of n 3D range face images of the database, which are first order objects. Each object Гi G Q, l = 1,2,..., n , is described by a matrix   Al

(l = 1,2,..., n), where each component Yab,a=1,2,...M, and b=1,2,…,N, is a single valued variable representing the 3D range values of the face image Гl. An image set is a collection of face images of m different subjects and each subject has different images with varying expressions and illuminations. Thus, there are m number of second order objects (face classes) denoted by E = {C,,C-,,...,C } , each consisting of different 1, 2, , m individual images, Гi gQ , of a subject. The face images of each face class are arranged from right side view to left side view. The feature matrix of kth sub face class ci of i‘h face class Ct, where k = 1,2,...,q , i = 1,2,..., m , is described by a matrix Xi of size M X N that contains interval variable akb , a = 1,2,...,M , and b = 1,2,...,N [26]. The matrix is called as symbolic face and is represented as :

X i^k

a i^k 11 .

k a iM 1

k i1N

a iMN

The interval variable aikab of kth sub face class cik of th                      kk    k   k i                               iab i            iab ,iab , where k and k are minimum and maximum iab            iab intensity values, respectively, among (a, b)th feature th                                 th inside the k sub face class of i face class. Thus, we obtain the qm symbolic faces from the given image database. Now, we apply LDA method to the centers xkab G R of the interval [ xkb, xi^b ] given by

kc iab

kk x iab + x iab

The M X N symbolic face Xk containing the centers kc of the intervals   k of symbolic face iab                                  iab

X _i ^k is given by

X i^k

k^c a i 11

.

k^c a iM 1

k^c i 1 N

a iMN

In the symbolic LDA approach, to calculate the scatter (within and between class) matrices of qm symbolic faces Xik , where i=1,2,…,m and k=1,2,…,q, we define the within-class image scatter matrix Sw as mq

S = £z ( x k - m ) T ( x k - m , )           ⁽⁸⁾

i = 1 k = 1

1q c where M. =— E Xi , and the between-class image qt= scatter matrix Sb as

m

S b = E ( M i - M ) ^T ( M , - M ) ,            (9)

i = 1

where

M = — E xk qm ,k

. In discriminant analysis, we

want to determine the projection axis that maximizes the det{Sb} det{Sw}

ratio

. In other words, we want to maximize the between-class image scatter matrix while minimizing the within-class image scatter matrix. It has been proved that this ratio is maximized when the column vector of projection axis V is the eigenvector of Sw Sb corresponding to first p largest eigenvalues. For each symbolic face X k , the family of projected feature vectors, Z1, Z2,..., Zp are considered as:

Z s = X , V _s

where s=1,2,^,p. Let B k = [ Z 1 , Z 2 ,..., Z_p ] , which is called as the feature matrix of the symbolic face X ^k .

The feature matrix of the test image is test                            g test obtained as following :

Btest = [ Z (test )1, Z (test )2,-, Z(test) p ]                    dD where                 , s=1,2,…,p.

( test ) s        test s ,      , ,…,p.

D.    AdaBoost Class f er

AdaBoost (Adaptive Boosting) is an ensemble learning algorithm that can be used for classification or regression. Although AdaBoost is more resistant to overfitting than many machine learning algorithms, it is often sensitive to noisy data and outliers. AdaBoost is called adaptive, because it uses multiple iterations to generate a single strong learner. AdaBoost creates the strong learner by iteratively adding weak learners. During each round of training, a new weak learner is added to the ensemble and a weighting vector is adjusted to focus on examples that were misclassified in previous rounds [27].

AdaBoost learning essentially works for a two class classification problem. Since face recognition is a multiclass problem, we convert it into one of the two classes using the representation of intra-personal Vs extra-personal classes. Intra-personal examples are obtained by using differences in images of the same person, whereas extra-personal examples are obtained by using differences in images of different people. From the depth Gabor images and intensity Gabor images under each scale and orientation, the effective features in this scale and orientation are selected. After effective depth and intensity Gabor features selected, the cascaded AdaBoost learning procedure is used to create a strong classifier with a cascading structure.

• E.    Proposed Method

The proposed methodology comprises the following steps:

• 1)    Radon transform is applied to the input depth and intensity images of a 3D face, which yields binary images that are used to crop the facial areas in the corresponding images.

• 2)    Gabor filter are applied to the cropped facial images, which yield Gabor magnitude features as facial feature vectors.

• 3)    Symbolic LDA is applied to the facial Gabor features in order to achieve dimensionality reduction and obtain subsampled feature vectors.

• 4)    Lastly, AdaBoost is used to perform face recognition based on subsampled feature vectors.

The algorithms of the training phase and the testing phase of the proposed method are given below:

Algorithm 1: Training Phase

• 1.    Input the depth and intensity images of a face from the training set containing M depth images and M intensity images corresponding to M faces.

• 2.    Apply Radon transform, from    ⁰⁰   to

  ¹⁸⁰⁰ orientations (in steps of h), to the input images yielding the corresponding binary images.

• 3.    Superpose the binary images obtained in the Step 2 on the corresponding input images to obtain the cropped facial images.

• 4.    Repeat the Steps 1 to 3 for all the M facial images

• 5.    Apply Gabor wavelet filter on ¹ set to extract Gabor magnitude features.

• 6.    Apply Symbolic LDA to subsample the Gabor feature set to reduce the dimensionality of the feature set. Let p be the reduced dimensionality of feature set.

• 7.    Compute the weights w ¹ , w ² ,...,    ^p for each

• 8.    After effective Symbolic LDA features are selected, the cascaded AdaBoost learning procedure is used to create a strong classifier.

in the training set and build the set 1 of cropped facial images.

training image as its facial features and store these values in the Symbolic LDA feature library of the face database.

Algorithm 2: Testing Phase

• 1.    Input the depth and intensity images from the probe set containing test images.

• 2.    Apply Radon transform, from    ⁰⁰   to

  180⁰ orientations (in steps of h), to the input images yielding the binary images.

• 3.    Superimpose the binary images on the corresponding input depth and intensity images to obtain the cropped facial images.

• 4.    Apply Gabor wavelet filter on cropped facial images to extract effective Gabor features.

• 5.    Compute the symbolic weights

  test

  w, , i ■ 1,2,..., p

  
  

  for the extracted Gabor

  
  

• 6.    Apply AdaBoost procedure and select the most effective features from redundant feature subspace. Compute the difference with each gallery example and form a difference vector v .

• 7.    Apply Nearest Neighbor scheme to decide which class the test sample belongs to and output the texture face image corresponding to the recognized facial image of the training set.

magnitude features by projecting the test image on the Symbolic LDA feature subspace of dimension p.

• IV.    EXPERIMENTAL RESULTS AND DISCUSSION

  As in typical biometric systems, the proposed method includes two phases: the training phase and the testing phase as illustrated in the Fig. 1. The proposed method is implemented using Intel Core 2 Quad processor @ 2.66 GHz machine and MATLAB 2012b. The 4059 images of three databases, namely, Bhosphorus 3D face database, CASIA 3D face database and Texas 3D face database, that are divided into three subsets: the training set, the

  gallery set and probe set. The training set contains 3200 images, corresponding to the 123 subjects with 33 images for each subject. The gallery set contains 100 images from the first images of other subjects. The other 759 images are randomly chosen as probe set from all the three databases.

The training process is performed once on a predefined training set to learn an effective classifier. It includes three important procedures: preprocessing, feature extraction and feature selection. By translating and rotating one input 3D image to align one reference 3D image, face poses and changed positions between the face and the equipment are normalized. This step is fully automatic. According to the aligned images, the normalized depth images and intensity images are obtained. Robust feature representation is very important to the whole system. It is expected that these features are invariant to rotation, scale and illumination. The proposed method uses raw depth and intensity features to describe the individual information using Gabor filters with multiple scales and multiple orientations. As it is commonly a problem, the method using multiple channels and multiple types of local features results in a much higher dimensional feature space. A large number of local features can be produced with varying parameters in the position, scale and orientation of the filters. Some of these features are effective and important for the classification task, where as others may not be so. The proposed framework combines Symbolic LDA and AdaBoost learning to fuse 2D and 3D Gabor features at the “feature” level.

During the testing phase, an input is classified according to the learned classifier in the training phase. By preprocessing, normalized depth image and intensity images are obtained. This procedure is the same as that in the training phase. The feature vector of one probe sample is generated by extracting the corresponding features as in the final cascaded classifier, and its difference with each gallery example forms the difference vector x . For each vector x , the i ^th layer of the cascaded classifier returns the similarity measure S_i . The larger this similarity value, the more this sample belongs to the intra-personal space. If S i <  0 , the i ^th layer rejects the sample. Using the similarities from the multiple layers, we can obtain its total similarity:

L

S = E S ,

¹ ■ ' (12)

where L is the number of layers and S_i is the similarity value from the i ^th layer. Thus, we can obtain the sample's similarity with each gallery example. Then, the nearest neighbor scheme is used to decide which class the test sample belongs to.

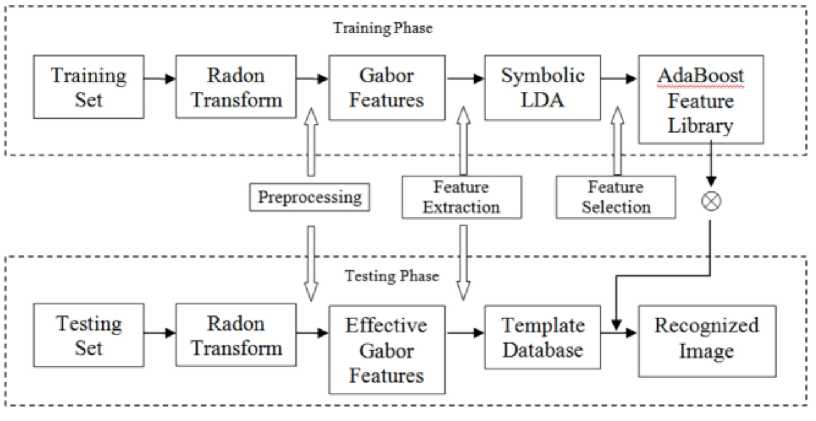
Figure 1. Overview of proposed framework

The sample training depth images of Bosphorus 3D face database which are used for the experimentation are shown in the Fig.2, and sample texture images corresponding to the face images of the Fig.2 are shown in the Fig.3. The different pose variations in the database are shown in the Fig.4.

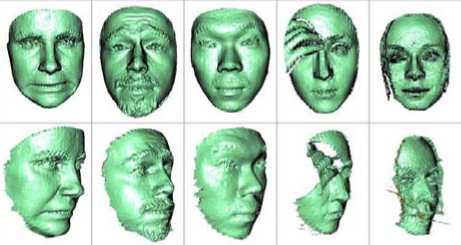
Figure 2. Sample training depth images in Bosphorus 3D face database

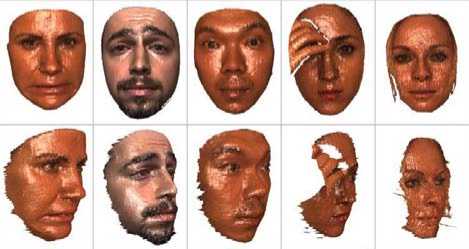
Figure 3. Sample texture images corresponding to the face images of the Fig. 2

The experimentation of the proposed method has been done with the chosen training, testing and probe sets of 3D face images, which yields the recognition accuracy of 99.65%. The Table 1 shows the performance comparison of the proposed method with other methods reported in the literature.

Table 1. The performance comparison of proposed method with other methods.

Method	3D Database Used	Verification rate
Kakadiaris et al. [28] Deformab le Model	Own Data Set	97.00%
Faltemier et al. [6] Region Ensemble	FRGC v2	94.90%
Maurer et al. [14] Deformab le Model	FRGC	95.80%
H. usken et al. [29] 2D and 3D fusion	FRGC	97.30%
Mian et al.[30] 2D and 3D fusion	CASIA	99.30%
Proposed Method Radon transform, Symbolic LDA, AdaBoost	Bosphorus, CASIA,Texas	99.65%

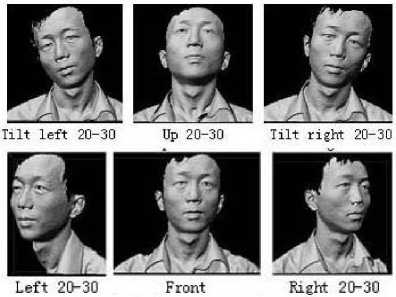
Figure 4. Pose variations considered in Bosphorus 3D face database

While symbolic data analysis approach captures image variability effectively, the LDA leads to feature dimensionality reduction and class separability enhancement. Hence, the proposed method has yielded significant recognition accuracy.

• V.    CONCLUSION

Intensity information is more pertinent than depth information in the context of expression variations; depth information is more pertinent than intensity information in the context of pose variations. Thus, their combination is helpful in improving recognition performance. In this paper, a new scheme is proposed to combine depth and intensity features in order to overcome problems due to expression and pose variations and thus build a robust and automatic face recognition system. The Gabor features are used in which the dimensionality of the Gabor features is extremely large since multiple scales and orientations are adopted. To reduce the large dimensions of Gabor features we propose a hierarchical selecting scheme for selecting effective features by using Symbolic LDA and AdaBoost procedures and constructed the classifier. This is one attempt to apply statistical learning to fuse 2D and 3D face recognition at the “feature” level. The experimental results are compared those of the existing methods for the 3D face recognition with the complex variations in the face, and demonstrate the significant effective performance of the proposed scheme. The recognition accuracy can be further improved by considering a larger training set and a better classifier.

ACKNOWLEDGMENT

The authors are grateful to the referees for their helpful comments and suggestions. Also, the authors are indebted to the University Grants Commission, New Delhi, for the financial support for this research work under UGC-MRP F.No.39-124/2010 (SR).