Design & Optimization of Reversible Logic Based ALU Using ACO
Автор: Shaveta Thakral, Dipali Bansal
Журнал: International Journal of Information Engineering and Electronic Business(IJIEEB) @ijieeb
Статья в выпуске: 6 vol.8, 2016 года.
Бесплатный доступ
Portable consumer electronics is most demanding in every segment of electronic industry and to satisfy the needs of low power electronics, comprehensive approaches and techniques have been proposed by various researchers. Reversible logic is one among emerging and competent technologies with profound applications in fields of computer graphics, optical information processing, quantum computing, DNA computing, ultra low power CMOS design and communication. ALU is a fundamental component of all processing units. Portability in computing system highly demands for reversible logic based ALU. Many researchers have proposed exact synthesis approaches of ALU design based on reversible logic but few have come up with reduced quantum cost without long computation overhead. Here in this paper heuristic approach has been used which not only provides solution for large number of variables but also avoids sufferings caused by long computation overhead. The main goal of this paper is to propose reversible logic based ALU and further it is optimized by Ant Colony Optimization (ACO) algorithm combined with Depth First Search (DFS) in terms of reduced quantum cost.
Ant colony optimization, Arithmetic logic unit, Depth first search, Quantum cost, Reversible logic
Короткий адрес: https://sciup.org/15013488
IDR: 15013488
Текст научной статьи Design & Optimization of Reversible Logic Based ALU Using ACO
Published Online November 2016 in MECS DOI: 10.5815/ijieeb.2016.06.07
Landauer proposed that “Amount of energy dissipated for every bit erasure during an irreversible operation is given by KTln2 joules where K is Boltzman’s constant and T is the operating temperature. Bennett provided the solution to Landauer statement that “The KTln2 energy dissipation would not occur, if computation is done in a reversible manner since amount of energy dissipated in a system depends directly on numbers of bits erased during computation”. Classical gates like two input AND, OR, NAND, NOR, XOR and XNOR are irreversible as input states from output states can’t be uniquely reconstructed.
Here two-bit input state is mapped to one-bit output state leads to the erasure of one bit and consequently loss of energy. This energy loss can be avoided by mapping n bit input states to n bit output states so that input states can be uniquely recovered from output states and under such circumstances, a gate is said to be reversible. The Main feature of reversible logic highlights number of inputs must be equal to number of outputs, no fan out is allowed and every output must be used only once. Section A briefs about reversible logic gates and section B introduces with multicontrol Toffoli gate.
-
A. Reversible Logic Gates
It is very important to know that out of four 1*1 one-qubit gates; only two are a reversible i.e. trivial gate and not the gate. Similarly out of 256 possible 2*2 two-qubit gates; only 24 are reversible. There exist 16777216 different 3*3 three-qubit gates however number of reversible 3*3 gates is much smaller i.e.40320.
-
B. Multi control Toffoli Gate (n*n)
An n*n reversible gate has n inputs and n outputs. In multi control Toffoli (MCT) gate first n-1 bits are known as control bits and generally last bit i.e nth bit is known as target bit although nth bit is mentioned just for simplicity and it could be any of n bits. Multi control Toffoli gate passes all the input bits to output and inverts the target bit when all control bits are 1.A multi control Toffoli gate may have one or more negative controls. I t means all the bits get passed to output when all positive control bits are 1 and negative control bits are 0.Symbol is put on target line; * is put for positive control and о is put for negative control. Generally Toffoli gate is represented by TOF (c: t) where c is set of control bits and t is target bit.Toffoli network consists of three basic gates as TOF1(X) called as NOT gate shown, TOF 2(X: Y) called as CNOT gate or Feynman gate and TOF 3 (X, Y: Z) called as Toffoli gate Primitives of Toffoli network for reversible logic synthesis are shown in Fig.1.
|
------е------ NOT gate (TOFl(XJ) |
X |
x - |
P = X |
||
|
O. = Y |
|||||
|
CNOTgate (TOF2(X:Y)) |
-Q = Хф Y |
Toffoli gate |
D (TOF3(X,Y:Z)) |
П AT L |
|
Fig.1. Primitives of Toffoli network for reversible logic synthesis
Some popular reversible logic gates that are used in proposed design of ALU are given in Table 1 with their specification, expression, quantum cost and quantum implementation.
Table 1.Popular Reversible Logic Gates in ALU Design
|
Reversible Logic Gate |
Specification |
Expression |
Quantum Cost |
Quantum Implementation |
|
NOT gate |
1*1 |
P = A |
1 |
А ф P A |
|
CNOT Gate/Feynman Gate |
2*2 |
P = A Q = А Ф В |
1 |
*-----A------ P=A В---Ф---- Q=A®B |
|
Toffoli/CCNOT Gate |
3*3 |
P = A Q = B R= АВФС |
5 |
Д -------•------------ --------- а- Г ' -L J-.1^-^ c------- v .---- v ----■ v* ------ » Quantum implementation of Toffoli Gate |
|
Fredkin Gate/CSWAP Gate |
3*3 |
P =A Q=AE® AC R = АСфАВ |
5 |
e H H > ' 1 ' (>-------- ' 1 ' -J— " Quawum кч«йлмлш»оп ol fredun Gate |
-
II. Related Work
Ant Colony Optimization is based on the behavior of nature given heuristic, like Ants follow the shortest path toward the food from source, also taken into account, the feasibility and the shortest path to reach the food. Ants decide to travel for the destination/food according to the visibility and the feasibility. There may be different paths for reaching the destination but the ants choose the shortest and the hurdle free path to reach destination. The ants lay down the pheromones on the path they travels the other ant follows the trail laid down by the ant. So using the similar technique that ants use to reach their destination, the algorithm implements the way to deliver the optimal solution/path for the given problem. To employ the best path several parameters are to be accounted.
Several approaches have been proposed by various authors for reversible logic based ALU design. Min Li [1] focused on the search for the best path of reversible logic synthesis using ACO. This technique is superior to previously proposed ones. Mayukh Sarkar [2] proposed a technique to synthesize Reversible circuit; first, the classical Boolean logic is converted using synthesis method and then Quine-McCluskey method is used for depth search and the breadth search in ACO. The results are found to be very satisfying. In paper [3], Ant colony optimization is explained in two different perspectives, the authors of paper [1] has also taken reference from this work. This article gives the guarantee for the optimal or optimal near solution for the synthesis of the problem. ESOP method is proposed by K. Fazel [4] for the cascaded structure that enables the function to be converted into EX-OR form. This allows forming the reversible circuit using cascading of Toffoli gate, this algorithm is found to be fast and use simple cost metric heuristic using divide and conquering rule. Ravi Raj Singh [5], proposed ALU circuit via the use of nanotechnology and quantum computing with minimum power dissipation; the reversible approach results in the improved computer; carry save adder is used to implement the ALU design and also to minimize the Quantum cost. Paper [6] proposed and verified reversible logic gate; ALU design with ripple carry adder has also been implemented.Zhijin Guan [7] discussed the construction of ALU based on reversible logic gates, traditional OR, AND and other gates are replaced by reversible logic gates; the aim was to reduce the power consumption. A function generator is constructed to reduce the effort of an adder used in the circuit. The comparison has been made between the results of classical ALU and their proposed ALU; the power consumption has been found to be quite less. The proposed ALU in the paper [8] consists of multiplexers and the control signals generated by a control unit which controls the operands to be manipulated.
It has been concluded that several approaches have been proposed by various authors for reversible logic based ALU designs. Yet lot of scope is there to improve quantum cost of ALU. In this paper an ALU design is proposed and after applying ACO algorithm it is optimized in terms of various parameters like number of gates, quantum cost, logic operations and garbage outputs. Section A briefs about popular reversible logic gates used in ALU designs. Section B briefs n*n multicontrol Toffoli gate and section C gives background on ant colony optimization.
Section III presents proposed methodology for reversible logic synthesis i.e. ACO the Meta heuristic method of search and optimization.
-
III. Proposed Methodology
In proposed ACO approach the path found by the artificial ants will be the shortest path in the form of a synthesized reversible function. The ants selectively choose the path i.e. Toffoli gate during the search from the library that is created. The decisions of ants are based on the availability and the pheromone quantity which will gradually increase with the selection of the ants. More number of ants decide to travel from the path more the strength of pheromone that path will have. To guide ants efficiently the pheromone table is constructed in which the pheromone values are updated (either increased or decreased). When the ants have traveled the whole path, if they reached the destination or near to destination the pheromone table will be updated. The pheromones will favor the path of the other ants for selection of gate.
-
A. Pheromone Table
This table is used to manage the pheromone levels of the ants traveling the path and also helps in defining the shortest path, i.e. the functions of Toffoli gates and number of gates to be used in implementing the circuit/function. There will be pre defined amount of pheromone in the table every time the ACO update the pheromone table the value of pheromone will be decreased or be increased. And the gate with the target value will be updated. The artificial ants do the randomize walk through whole path of the derived graph by ACO, the ants lay down the pheromones on the path by selecting favorable Toffoli gate.
Pheromone trails are associated with the connection of the components; more the quantity of pheromone more will be the probability of other ants to chose the trail. The same type of models is used before this and they have been proven efficient. At the same time the evaporation in pheromone will also take place if the less no of ant chose the path.
The pheromone update factor is given by:
P p = EVR x P p + P n
P p : previous pheromone value
Pn : new pheromone value
EVR : Evaporation rate
-
B. ACO Algorithm
At first most, initialize the pheromone table and now initialize the global loop that will make (G_loop), number of iterations of upper limit. Then number of fix ants are released to move and select the path by selecting the Toffoli gate and the output of the Toffoli will be the function that will provide path and the pheromone will be evenly distributed by all the ants i. The target bits of gates are been selected by probability function which is calculated using
[(wltCcSi.k))" X (Пс)^
L^oKwlj^CSv ^У x (nc)^
ifwt(csj,к) > 0
N
Where W ( cs , k ) = ^ ^ (^ , is the sum of pheromone i = 0
for tth bit.
The probability of selecting control bits of the selected toffoli gate is calculated using
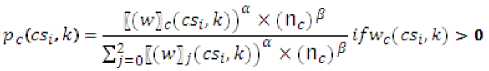
N
Where W c ( cs„ k ) = ^ ф ( s, , , ) ( t, m, cm ) , is the sum of i = 0
pheromone for the mth bit set as value c m when the tth bit is the target bit.
-
C. Proposed ALU Design
The ALU was designed using the reversible logic gates. This ALU supports following operations:
-
1. 7 arithmetic and
-
2. 5 logical operations
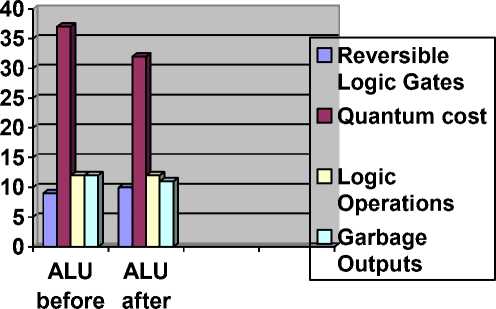
The quantum cost of proposed ALU is 37. This quantum cost shows complexity of the design.
It is necessary to optimize the design. There are many factors on which the efficiency of the design depends like size, number of gates, number of garbage outputs, quantum cost etc.Here work is not taking all of those into account but as much as we can do to optimize the design to get better and more effective performance.
-
D. ACO applied on ALU for Optimization
The goal of this optimization is to decrease the gate count which will ultimately decrease the quantum cost and increase the efficiency of the circuit.
The total of i ants are employed. Finding the route each ant i till the L_loop (local loop) is terminated or the disti becomes ‘0’. Which means ants reached the fI i.e. identity function, at the iteration index L_loop. The local search is implemented at lines8-17, which nests depth-first searches in a breadth-first search controlled by parameters BREADTH and DEPTH, respectively. Each ant i will evaluate the breadth and depth of every function and the best route, there may be some loops or repeated path are formed delete those paths and loops, mentioned in line 20-21, now after removal of loops updated the route and pheromone every time in the pheromone table, line 23.
-
E. Working of Proposed ACO
ACO is employed to overcome the above mentioned problem to achieve the goal. This method has proven effective for solving many difficult combinatorial
Optimization problems. Algorithm works in some different fashion that it is used to take the output function of a circuit as its input and the output of the ACO will be the input function of the circuit. To achieve this goal certain parameters are applied.
The algorithm is architected in a linear phase manner. Firstly, a pheromone table is implemented than ACO algorithm that will employ this implemented pheromone table to update the ant path and defining he shortest path for the solution. The algorithm and the pheromone table are explained in above sections. This can be understood with the help of an example.Let the function be f(n) = {4,1,7,5,2,6,0,3}, the optimization algorithm is to be applied on f(n). Table2, showing the truth table for the reversible function.
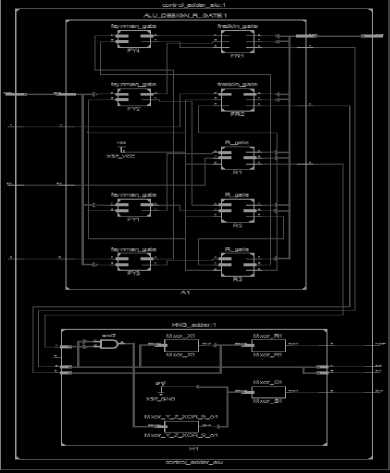
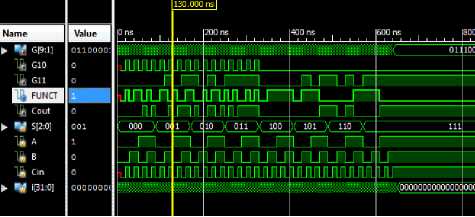
Step1. initialize pheromone table step2. repeat K Final State step5. start CS of the function step6. CSi as ‘P’ for ants and initialize the routei. step9. j = 1 for all the childs step10. CSi =toffoli_func(lif) step11. CSi =toffoli_func(CSi) step12. addCSi to routeij step13. if (dist (CSi) step14. disti = dist (CSi) step15. best_route = j step16. end if step17. go to step8 step18. go to step3 step19. take the routei step20. remove the loop, if formed step21. add the best_route to routei step22. end for step23. do pheromone update step24. end Fig.2. Proposed ACO Algorithm The ants which algorithm is employing will select a promising Toffoli gate, having t as a target bit and ck as control bits, where k is number of control bits, through the probability function explained above. All the ant will try to find the path to reach its destination which is the identity function fI = {0, 1, 2, 3, 4, 5, 6, 7}, each ant having specific amount of pheromone will lay down the pheromones and move towards the destination. The ants will travel according to the Tour_graph, figure 1.3; give the idea about the graph is having the virtual paths and non virtual paths. Virtual paths and non virtual path is calculated using hamming distance between the states. The selection of the path will be according to Tour_graph.When one ant will complete its tour then the route will be updated, the other ants will also do the same process following the trails of the ants having the more amount of pheromone. When all the ants have completed the tour then pheromone table will be updated for the next tour. This technique helps us to find the optimal path without searching whole space by using the probability and the pheromone values. Once ants reach the destination fI, then the shortest path will be updated. Table 2. Reversible function f(n) ={4,1,7,5,2,6,0,3} X Y Z X Y Z 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 1 1 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 1 1 1 0 1 1 0 0 0 0 1 1 1 0 1 1 Fig. 4 shows here the path searched by ants to reach the destination, the shortest path traced by the ants and with the highest value of pheromone is give by 4 Toffoli gate. There are different paths shown but the shortest path is traced by the ants. The algorithm gave the advantage, not to search whole space of the possibilities but the most probabilistic path using heuristic. After implementation of ACO the shortest path is obtained, the traced path is given by Toffoli gates and its target bit and the control bits with its polarity value. It is then converted into circuit. The circuit can be optimized more as it is having the Toffoli gates that are of 5x5 and 4x4due to which quantum cost is not decreased to that extent. They can be replaced by their equivalent as shown in Fig.5.Circuit of ALU consist of 10 reversible logic gates including four Feynman gates, three R gates, two Fredkin gates and one HNG gate. Circuit can perform total 12 operations including seven arithmetic and five logical operations. Fig.5. Block Diagram of ALU Fig. 6 shows the RTL view of the ALU implemented after applying ACO. RTL schematic is designed to understand the architecture of the design. The RTL view gives us the idea about implemented design and also it gives the tree synthesis that how these all are connected. It allows visual representation of the design. The schematic is designed for the top level module. The Fig. 7 shows the output waveform of the functional ALU design after implementation of ACO. The Toffoli circuit is converted into other gates to make ALU more efficient and to reduce the delay. It provides Quantum Cost of 32. By applying ACO the quantum cost is reduced by 5. Fig.7. Simulation waveform Table 3. Comparison Table ALU DESIGNS ALU before ACO ALU after ACO No. of Gates 9 10 Quantum Cost 37 32 Logic operations 12 12 Garbage O/Ps 12 11 Type of Gates Used Toffoli, Feynman, Fredkin Feynman, Fredkin, R-Gate, HNG Table 3 gives the detailed picture of the ALU implemented before and after ACO synthesis, the major parameters affecting ALU performance are being compared here in the table. Some Toffoli gates also been replaced by other gates for the sake of quantum cost. Table 4 and table 5describe the logical function table and the arithmetical function table respectively. After ACO although one gate is increased yet it provides reduced quantum cost and reduced number of garbage outputs which are considered to be two top most optimization metrics demanded by latest reversible circuits. Table 5. Function Table for Arithmetic Operations S0 S1 S2 Cin Output Function 0 0 0 0 A Transfer A 0 0 0 1 A+1 Increment A 1 0 0 0 A+B Addition 1 0 0 1 A+B+1 Add with Carry 0 1 0 0 A+B' Subtract with Borrow 0 1 0 1 A+B'+1 Subtraction 1 1 0 0 A-1 Decrement A Table 4. Function Table for Logical Operations S0 S1 S2 Г; in Output Function 0 0 1 x A+B OR 1 0 1 x A.B AND 0 1 1 x А Ф В XOR 1 1 1 x A' NOT 1 1 0 1 A Transfer A In this paper, Ant colony optimization algorithm has been proposed on ALU design; the optimization approach is probabilistic and is formulated for the ALU using reversible gates. This method of optimization does not search the whole space but selects the paths according to decision made by ACO and gives the optimization in the form of reduced quantum cost as shown in Fig.8. ACO ACO Fig.8. Optimization metrics comparison before & after ACO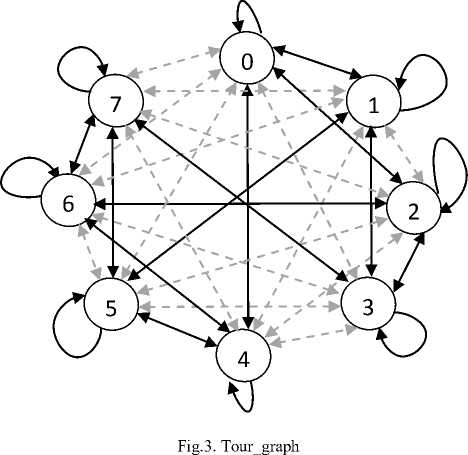
IV. ALU After ACO Implementation
V. Simulation & Result Analysis
VI. Conclusion
Список литературы Design & Optimization of Reversible Logic Based ALU Using ACO
- M.Li, Y. Zheng, MS. Hsiao and C. Huang, "Reversible logic synthesis through ant colony optimization," Design, Automation & Test in Europe Conference & Exhibition; 8-12 March 2010; Dresden.Europe: IEEE, pp.307-310.
- M. Sarkar, P. Ghosal, SP. Mohanty, "Reversible circuit synthesis using ACO and SA based quine-mcCluskey method," IEEE 2013 56th International Midwest Symposium on Circuits and Systems; 4-7 August 2013; Columbus.OH, IEEE.pp.416-419.
- WJ. Gutjahr,"ACO algorithm with guaranteed convergence to the optimal solution," Information Processing Letters, 82(3):145–153,2002.
- K. Fazel, M. A. Thornton, J. E. Rice, "ESOP-based Toffoli Gate Cascade Generation," IEEE 2007 Pacific Rim Conference on Communication, Computers and Signal Processing;,22-24 August 2007;Victoria.BC: IEEE.pp.206-209.
- R. Singh, S.Upadhyay, S.Saranya S, Soumya, KB.Jagannath, SA. Hariprasad,"Efficient Design of Arithmetic Logic Unit using Reversible Logic Gates," IJARCET 2014, vol. 3, pp. 1474-1477
- M.Matthew, L.Matthew,M. Richard and R.Nagarajan,"Design of a Novel Reversible ALU using an Enhanced Carry Look-Ahead Adder," 11th IEEE International Conference on Nanotechnology; 15-18 August 2011; Portland.Marlott:IEEE.pp.1436-1440.
- Z. Guan, W. Li, W. Ding, Y. Hang, L.iNi,"An arithmetic logic unit design based on reversible logic gates," Pacific Rim Conference on Communication, Computers and Signal Processing; 23-26 August 2011; Victoria.BC:IEEE.pp.925-931.
- Y. Syamala, A. V. N. Tilak, "Reversible arithmetic logic unit," 3rd International conference on Electronics Computer Technology(JCECT);8-10 April,2011;Kanyakumari:IEEE.pp.207-211.
- MB. Ali, MM. Hossin and ME> Ullah," Design of Reversible Sequential Circuit Using Reversible Logic Synthesis", International Journal of VLSI design & Communication Systems (VLSICS) Vol.2, No.4, December 2011
- F. Sharmin, RK. Mitra, R. Hasan, A. Rahman "Low cost reversible signed comparator" International Journal of VLSI design & Communication Systems" Vol.4, No.5,pp:19- 33,2013
- B.Dehghan, A.Roozbeh, J. Zare "Design of low power comparator using DG gate" Scientific research ciruits and systems doi.org/10.4236/cs.2013.51002pp: 7-12, 2014
- N. Pandey, N.Dadhich, MZ. Talha "Realization of 2-to-4 reversible decoder and its applications" International Conference on Signal Processing and Integrated Networks (SPIN) pp: 349- 353, 2014
- V. Oklobdzija, "High -Speed VLSI Arithmetic Units: Adders and Multipliers", in "Design of High -Performance Microprocessor Circuits", Book Chapter, Book edited by A. Chandrakasan, IEEE Press, 2000.
- M. K. Thomson, Robert Gluck and Holger Bock Axelsen,"Reversible arithmetic logic unit for quantum arithmetic", Journal of Physics A: Mathematical and Theoretical. Vol.43, 2010.
- Towards a Design Flow for Reversible Logic -Robert Wille and RolphDrechsler, ISBN: 978-90-481-9578-7 Springer Dordrecht Heidelberg London New York


