Design and Implementation of an Intelligent Mobile Game

Published Online March 2017 in MECS DOI: 10.5815/ijmecs.2017.03.02

• I.    Introduction

  Mobile games on mobile devices, which are provided to users via mobile communication network and described as electronic games, have significantly developed along with the indispensable spread of especially mobile devices with 3G support in our daily lives [1]. Mobile games have been able to sustain their development thanks to mobile features such as portability, ease of use and simplicity and user habits formed over time [2]. While they appealed to a certain number of users with the Snake game, Tetris game etc. at the end of 20th century, they have been one of the prominent platforms in game market on the world by accessing to 1.5 billion users around the world in 2014 according to the data of Global Mobile Game Industry [3].

It has been very important to appeal to users of thousands of games released by their developers every day, sustain their existence in the market and provide the qualifications to find a place in the market. Games are designed in accordance with certain rules. In order to design a successful game, these rules are based on entertaining the users with interesting scenarios and visual-audial features [4]. It is also possible to benefit from several disciplines for forming these rules. Games that can appeal to users’ interests can be designed as mobile game by using clustering which is a data mining method and has several application fields.

Clustering, which is an unsupervised learning method because of the lack of identified clusters and accurate knowledge of the number of clusters [5], is described as categorizing objects in a data set into clusters according to their similarities based on a certain distance measure [6]. While the intra-cluster similarity is maximum in the formed clusters, the inter-cluster similarity is minimum. If these conditions are provided, clustering can be successful, otherwise, it is unsuccessful. Clustering, which is an important method in information inference with all these features, has several application fields such as pattern recognition, bio-information, text mining and machine learning [7, 8].

The remaining part of the study is organized as the following: In the 2nd part, the clustering methods used are described. In the 3rd part, evaluation measures for data sets and clustering algorithms are described. In the 4th part, the experimental results are presented. In the 5th part, the contributions of the study are given.

• II.    Method

• A.    K-Means Algorithm

  K-means algorithm is one of the widely used algorithms in data mining. It was developed by J.B. MacQueen [14] in 1967. Its aim is to separate the data set given to it as input into k number of clusters. The k parameter in the name of the algorithm stands for the cluster number to be obtained at the end of the clustering process. K-means algorithm works on the logic of forming clusters according to the distance to the point which is determined as center for each class. The distance of the objects of clusters to the central point also stands for the amount of error. The aim is to minimize the distance between objects of the cluster and maximize the distance between the clusters.

The algorithm consists of four main steps [15]: These are determining center of clusters, assigning the points out of the central point to clusters according to their distance to the center of clusters, calculation of the new center of clusters after each iteration and the iteration of processes till obtaining resolute center of clusters. The flowchart of K-means algorithm is presented in Fig. 1.

The biggest problem of K-means algorithm is determining the start point. If there is a bad choice at the beginning, changes will be too frequent in clustering process and in this situation, different clustering results will be obtained every time with the same number of iterations and different start points. Moreover, the algorithm may not provide good results if the dimensions and density of data groups are different and there are conflicts in the data. Besides, the complexity of K-means algorithm is less than the other clustering methods and realization of the algorithm is easier.

The time complexity of each iteration of K-means algorithm is stated as O( nkd ). Here the n value stands for the number of records in the cluster, k value stands for the number of clusters to be obtained and d value stands for the number of features in each record. As it can be understood from the parameters, the dimension of data set, number of feature in the data and the dimensions of the iterations have an effect on process time, but even if when the method is applied to very big datasets, results can be obtained very quickly.

In this study, Iterative K-means and Iterative Multi K-means were also analyzed in addition to K-means method. Iterative K-means algorithm works with minimum cluster number and maximum cluster number parameters to increase the accuracy of K-means algorithm. The method makes K-means algorithm work in minimum and maximum cluster number intervals and it calculates a score value for each cluster number. It gives the number of cluster which has the highest score value as a result. Iterative Multi K-means algorithm is a developed form of Iterative K-means algorithm in terms of iteration number. In a different way from Iterative K-means algorithm, it aims to obtain the best cluster number and the best iteration value for this cluster number by working with different numbers of iterations.

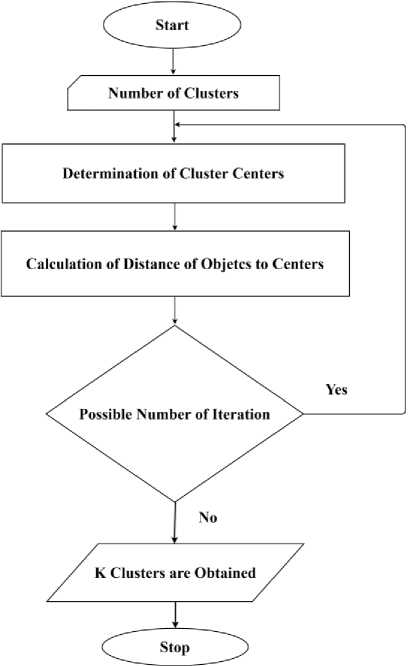
Fig.1. Flowchart of K-means algorithm.

• III.    Data Set and Evaluation Measures

The data set used in this study was specially formed for the game to be developed. There are hexadecimal values of 141 color codes in the data set. These values were categorized into the primary colors red, green and blue before they were used for clustering and then, converted to decimal forms. The obtained color values with three parameters were saved in a different file. The clustering process was realized according to the distance values between these three parameters.

There are different methods developed for the evaluation of clustering algorithms. Some of these are listed as process time, sum of center of clusters similarities, (SOCS), sum of error squares (SSE), AIC (Akaike’s Information Criterion) score and BIC (Bayesian Information Criterion) scores. Descriptions of these methods are given in Table 1.

Table 1. Methods Used for Evaluation of Clustering Algorithms

Method	Description
Process time	Refers to time it takes to cluster
SOCS	Refers to sum of center of clusters similarities
SSE	Refers to sum of distance of points to center of clusters in which they are found.
AIC and BIC	Refers to a measure of statistical model quality over a given dataset

While applying process time and SOCS described in Table 1, any of the methods for distance calculation can be utilized. The formula of SSE calculation method is given in (1). The k value in the formula stands for the cluster number, c_i value i. stands for the center of clusters and x value i. stands for the objects of cluster.

K

SSE =         x e c i dis tan ce ( x , c i )²

i = I

The formula of AIC evaluation method is shown in (2) and the formula of BIC evaluation method is shown in (3). The L value in (2) and (3) stands for the similarity calculation function used and the p value stands for the number of features in the data set.

AIC = - 2log L + 2 p (2)

The low AIC and BIC values show that the model is closer to reality and the use of these two parameters together is more efficient for the model or cluster number choices in evaluation.

BIC =- 2log L + log( « ) p (3)

The biggest advantage of AIC measure is that it is highly successful in both intra-cluster and inter-cluster evaluations. Both for the AIC and BIC equations, the second part of the equation calculate a penalty value for the elements that are included later. However, this value was determined as a low value for AIC while it is a higher value for BIC. With the high penalty value in the BIC equation, more accurate evaluation was aimed for big datasets.

In the context of the study, the comparison of clustering methods from different perspectives was conducted by the use of process time, SOCS and SSE evaluation methods. Java-ML (Java Machine Learning Library), which is the machine learning library of Java, was used for the realization of evaluation methods [19] and it was determined which method is more appropriate for the game to be developed.

• IV.    The Mobile Application Developed

The game developed is a simple ball blasting game. There are three levels of difficulty in the game. The difficulty levels are determined according to the dimension of the matrix appearing on the screen and the number of color clusters placed into the matrix. The difficulty levels of the game and the number of clusters corresponding to these difficulty levels are presented in Table 2.

The game realizes clustering process in the mobile environment according to the data set consisting of colors. When three or more balls in the same cluster come together vertically or horizontally, they blast. After the blast, the balls above replace the blasted balls and new balls in random colors are produced for the empty spaces at the top of the matrix. There is a time limit for each difficulty level in the game. Points are calculated considering the number of blasted balls and time taken to blast them. The screenshots of difficulty levels in the game are given in Fig. 3.

Table 2. Number of Clusters Corresponding to the Levels in the Game

Difficulty Levels	Dimension of Matrix	Number of Clusters	Time
Easy	6 X 6	3	30 minutes
Moderate	9 X 6	4	25 minutes
Difficult	12 X 6	5	15 minutes

a) Easy

b)Moderate

Fig.3. Screenshots of difficulty levels in the game

c) Difficult

• V.    Experimental Results

  In order to understand whether clustering algorithms are sufficient for the game to be developed in terms of performance and accuracy, some tests were conducted. Experimental tests were realized on a computer on which Intel(R) Core(TM) i5-3317U CPU @ 1.70 GHz, 8 GB RAM, 350 GB hard drive and Windows 7 Ultimate are uploaded.

It is necessary to choose the appropriate clustering method in order to obtain the cluster values mentioned in Table 2. For this reason, it was aimed to determine the most appropriate method by evaluating different clustering algorithms. The results obtained with the application of K-means algorithm on data set are presented in Table 3. There are process time and accuracy results of clusters obtained with different number of clusters in the table. When the process time column is examined, it is seen that the clustering process doesn’t affect the performance of the game. The process times obtained are shorter than even one second and if we consider that the clustering process will be done only once at the beginning of the game, its effect on the performance is little if any.

Evaluation results of K-means, Iterative K-means and Iterative Multi K-means are given respectively in Table 3,

Table 4 and Table5. It was observed that the algorithms have similar performances in terms of process time, the center of clusters obtained and closeness to reality. Therefore, it is observed that the use of Iterative K-means or Iterative Multi K-means algorithms instead of K-means algorithm will not cause a serious effect on the results.

Table 3. Evaluation Results of K-means Algorithm

k	Process Time (sec.)	SOCS	SSE	AIC	BIC
2	0,000715	127.72	3913076.84	14430,869276	14431,018495
3	0,000814	132.82	2780635.32	14286,456027	14286,605246
4	0,000735	134.88	2299393.45	14172,267740	14172,267740
5	0,000676	133.30	1908820.35	14083,520316	14083,669535
10	0,000706	137.81	1036044.67	14013,227955	14013,377174
15	0,001337	139.07	733983.47	14090,361464	14090,510683

Table 4. Evaluation Results of Iterative K-means Algorithm

k	Process Time (sec.)	SOCS	SSE	AIC	BIC
2	0,000721	127.32	3925900.84	14368,068617	14368,217837
3	0,000738	132.82	2780635.32	14286,456027	14286,605246
4	0,000705	133.14	2402667.46	14126,751763	14126,900982
5	0,000816	135.52	1991643.28	14150,740182	14150,889401
10	0,000691	138.03	1048043.83	14037,366551	14037,515770
15	0,000709	137.61	828138.95	14024,403325	14024,552544

Table 5. Evaluation Results of Iterative Multi K-means Algorithm

k	Process Time (sec.)	SOCS	SSE	AIC	BIC
2	0,000814	127.73	3912928.79	14434,115946	14434,265165
3	0,000737	132.82	2780635.32	14286,456027	14286,605246
4	0,000695	135.46	2290333.21	14189,547951	14189,697170
5	0,000783	133.52	1895319.41	14070,696099	14070,845318
10	0,000726	138.29	1036810.57	14023,875312	14024,024532
15	0,000762	138.93	734218.30	14082,862737	14083,011956

k	Process Time (sec.)	SOCS	SSE	AIC	BIC
2	0,001156	129.57	4171972.59	14683,482333	14683,631552
3	0,001286	131.05	3777599.33	14665,799503	14665,948722
4	0,000918	131.08	3628823.20	14662,039772	14662,188991
5	0,001353	131.24	3611538.37	14710,335577	14710,484796
10	0,001763	131.50	3422162.38	14782,823114	14782,972333
15	0,001565	131.80	3391581.89	14911,419501	14911,568720

• VI.    Results

In this study, which is developed to support mobile programming and the use of algorithms in mobile fields, it was revealed that the use of algorithms in mobile programming doesn’t affect performance and more professional games can be developed. Moreover, it was shown that clustering algorithms carry out clustering process more quickly and accurately for the game developed.