Design Computed Torque Controller with Parallel Fuzzy Inference System Compensator to Control of Robot Manipulator
Автор: ArmanJahed, FarzinPiltan, HosseinRezaie, BamdadBoroomand
Журнал: International Journal of Information Engineering and Electronic Business(IJIEEB) @ijieeb
Статья в выпуске: 3 vol.5, 2013 года.
Бесплатный доступ
Computed torque controller (CTC) is a significant nonlinear controller under condition of partly uncertain dynamic parameters of system. This controller is used to control of highly nonlinear systems especially for robot manipulators, because this controller is a robust and stable. Conversely, computed torque controller is used in many applications; it has an important drawback namely; nonlinear equivalent dynamic formulation in uncertain dynamic parameter. The nonlinear equivalent dynamic formulation problem in uncertain system can be solved by using artificial intelligence theorem. However fuzzy logic controller is used to control complicated nonlinear dynamic systems, but it cannot guarantee stability and robustness. In this research parallel fuzzy logic theory is used to compensate the system dynamic uncertainty in computed torque controller.
Computed Torque Controller, Robot Manipulator, Nonlinear Equivalent Part, Fuzzy Inference System, Compensator
Короткий адрес: https://sciup.org/15013188
IDR: 15013188
Текст научной статьи Design Computed Torque Controller with Parallel Fuzzy Inference System Compensator to Control of Robot Manipulator
Published Online September 2013 in MECS
E-mail: ;
-
I. Introduction
In modern usage, the word of control has many meanings, this word is usually taken to mean regulate, direct or command. The word feedback plays a vital role in the advance engineering and science. The conceptual frame work in Feed-back theory has developed only since world war ІІ. In the twentieth century, there was a rapid growth in the application of feedback controllers in process industries. According to Ogata, to do the first significant work in three-term or PID controllers which Nicholas Minorsky worked on it by automatic controllers in 1922. In 1934, Stefen Black
was invention of the feedback amplifiers to develop the negative feedback amplifier[3]. Negative feedback invited communications engineer Harold Black in 1928 and it occurs when the output is subtracted from the input. Automatic control has played an important role in advance science and engineering and its extreme importance in many industrial applications, i.e., aerospace, mechanical engineering and robotic systems. The first significant work in automatic control was James Watt’s centrifugal governor for the speed control in motor engine in eighteenth century[1-12]. There are several methods for controlling a robot manipulator, which all of them follow two common goals, namely, hardware/software implementation and acceptable performance. However, the mechanical design of robot manipulator is very important to select the best controller but in general two types schemes can be presented, namely, a joint space control schemes and an operation space control schemes[13-23]. Joint space and operational space control are closed loop controllers which they have been used to provide robustness and rejection of disturbance effect. The main target in joint space controller is design a feedback controller that allows the actual motion ( q a (t) ) tracking of the desired motion ( q d (t ) ). This control problem is classified into two main groups. Firstly, transformation the desired motion X d (t ) to joint variable q d (t ) by inverse kinematics of robot manipulators [6]. The main target in operational space controller is to design a feedback controller to allow the actual end-effector motion X a (t ) to track the desired endeffector motion X d (t ) . This control methodology requires a greater algorithmic complexity and the inverse kinematics used in the feedback control loop. Direct measurement of operational space variables are very
expensive that caused to limitation used of this controller in industrial robot manipulators[24-36]. One of the simplest ways to analysis control of multiple DOF robot manipulators are analyzed each joint separately such as SISO systems and design an independent joint controller for each joint. In this methodology, the coupling effects between the joints are modeled as disturbance inputs. To make this controller, the inputs are modeled as: total velocity/displacement and disturbance. Design a controller with the same formulation and different coefficient, low cost hardware and simple structure controller are some of most important independent-joint space controller advantages. Nonlinear controllers divided into six groups, namely, feedback linearization (computed-torque control), passivity-based control, sliding mode control (variable structure control), artificial intelligence control, Lyapunov-based control and adaptive control[1, 6, 37-44].
Computed torque controller (CTC) is a powerful nonlinear controller which it widely used in control of robot manipulator. It is based on feedback linearization and computes the required arm torques using the nonlinear feedback control law. This controller works very well when all dynamic and physical parameters are known but when the robot manipulator has variation in dynamic parameters, in this situation the controller has no acceptable performance[45-62]. In practice, most of physical systems (e.g., robot manipulators) parameters are unknown or time variant, therefore, computed torque like controller used to compensate dynamic equation of robot manipulator[1, 6]. Research on computed torque controller is significantly growing on robot manipulator application which has been reported in [1, 6, 15-16]. Vivas and Mosquera[15]have proposed a predictive functional controller and compare to computed torque controller for tracking response in uncertain environment. However both controllers have been used in feedback linearization, but predictive strategy gives better result as a performance. A computed torque control with non parametric regression models have been presented for a robot arm[16]. This controller also has been problem in uncertain dynamic models. Based on [1, 6]and [15-16]computed torque controller is a significant nonlinear controller to certain systems which it is based on feedback linearization and computes the required arm torques using the nonlinear feedback control law. When all dynamic and physical parameters are known, computed torque controller works fantastically; practically a large amount of systems have uncertainties, therefore sliding mode controller is one of the best case to solve this challenge.
In recent years, artificial intelligence theory has been used in sliding mode control systems. Neural network, fuzzy logic and neuro-fuzzy are synergically combined with nonlinear classical controller and used in nonlinear, time variant and uncertain plant (e.g., robot manipulator). Fuzzy logic controller (FLC) is one of the most important applications of fuzzy logic theory. This controller can be used to control nonlinear, uncertain, and noisy systems. This method is free of some model techniques as in model-based controllers. As mentioned that fuzzy logic application is not only limited to the modelling of nonlinear systems [31-36] but also this method can help engineers to design a model-free controller. Control robot arm manipulators using model-based controllers are based on manipulator dynamic model. These controllers often have many problems for modelling. Conventional controllers require accurate information of dynamic model of robot manipulator, but most of time these models are MIMO, nonlinear and partly uncertain therefore calculate accurate dynamic model is complicated [32]. The main reasons to use fuzzy logic methodology are able to give approximate recommended solution for uncertain and also certain complicated systems to easy understanding and flexible. Fuzzy logic provides a method to design a model-free controller for nonlinear plant with a set of IF-THEN rules [32-62].
Based on mechanical and control methodologies research in robotic system, mechanical design, type of actuators and type of systems drive play important roles to have the best performance controller. This section has focused on the robot manipulator mechanical classification. Types of kinematics chain, i.e., serial Vs. parallel manipulators, and types of connection between link and join actuators, i.e., highly geared systems Vs. direct-drive systems are presented in the following sections because these topics played important roles to select and design the best acceptable performance controllers [1, 6, 14]. A serial link robot is a sequence of joints and links which begins with a base frame and ends with an end-effector. This type of robot manipulators, comparing with the load capacity is more weightily because each link must be supported the weights of all next links and actuators between the present link and end-effector [1, 6]. Serial robot manipulators have been used in automotive industry, medical application, and also in research laboratories [1, 6]. In contrast, parallel robot manipulators design according to close loop which base frame is connected to the end-effector frame with two or more kinematic chains [6]. In the other words, a parallel link robot has two or more branches with some joints and links, which support the load in parallel. Parallel robot have been used in many applications such as expensive flight simulator, medical robotics (I.e., high accuracy, high repeatability, high precision robot surgery), and machinery tools [1]. Parallel links robot manipulators have higher accuracy and faster than serial links robot manipulators but the work space limitation in serial links robot manipulator is lower than parallel links robot manipulator. From control point of view, the coupling between different kinematic chains can generate the uncertainty problems which cause difficult controller design of parallel robot manipulator [1, 6]. One of the most important classifications in controlling the robot manipulator is how the links have connected to the actuators. This classification divides into two main groups: highly geared (e.g., 200 to 1) and direct drive (e.g., 1 to 1) [1]. High gear ratios reduce the nonlinear coupling dynamic parameters in robot manipulator. In this case, each joint is modeled the same as SISO systems. In high gear robot manipulators which generally are used in industry, the couplings are modeled as a disturbance for SISO systems [14]. Direct drive increases the coupling of nonlinear dynamic parameters of robot manipulators. This effect should be considered in the design of control systems. As a result some control and robotic researchers’ works on nonlinear robust controller design [2].
Normal combinations of fuzzy logic methodology (FLM) and computed torque controller (CTC) are to apply fuzzy pzrzllel compensator at the same time [17], while FLM compensates the control error, CTC reduce the error of fuzzy inference system such that the final tracking error is asymptotically stable [18]. The equivalent part is compensating, because CTC and FLM work parallel. In this paper, the asymptotic stability of CTC control with parallel fuzzy logic compensation is proposed (CTC+FLM). The fuzzy inference system is used to approximate the nonlinear plant. A dead one algorithm is applied for the fuzzy control. After the regulation error enter converges to the dead-zone, a super-twisting second-order computed torque control is used to guarantee finite time convergence of the whole control (FLM+CTC). By means of a Lyapunov approach, we prove that this type of control can ensure finite time convergence and less oscillation than CTC [33-39].
This paper is organized as follows; second part focuses on the modeling dynamic formulation based on Lagrange methodology, fuzzy logic methodology and computed torque controller to have a robust control. Third part is focused on the methodology which can be used to reduce the error, increase the performance quality and increase the robustness and stability. Simulation result and discussion is illustrated in forth part which based on trajectory following and disturbance rejection. The last part focuses on the conclusion and compare between this method and the other ones.
-
II. Theory2.1 Dynamic Formulation of Robot Manipulator
The equation of a multi degrees of freedom (DOF) robot manipulator is calculated by the following equation[6]:
M(q)q + N ( q , q ) = т (1)
Where т is n x 1 vector of actuation torque, M (q) is n x n symmetric and positive define inertia matrix,
N(q, q') is the vector of nonlinearity term, and q is n x 1 position vector. In equation (1) if vector of nonlinearity term derive as Centrifugal, Coriolis and Gravity terms, as a result robot manipulator dynamic equation can also be written as [55-62]:
N(q, q) = V(q, q) + G(q)
V(q, q) = B(q)[qq] + C(qMq]2
т = M^q + B(q)[qq ] + C(q)[q]2
+ G(q)
Where,
B ( q )is matrix of coriolis torques, C ( q) is matrix of centrifugal torque, [qq]is vector of joint velocity that it can give by: [qP q 2 , qr q 3 ,™., q 1 . q n , q 2 . q 3 , ]T, and [q]2 is vector, that it can given by: [q' 1 2,q22, q32, — . ]T.
In robot manipulator dynamic part the inputs are torques and the outputs are actual displacements, as a result in (4) it can be written as [1, 6, 50-58];
q = M 1(q).{T-jV (q, q)} (5)
To implementation (5) the first step is implement the kinetic energy matrix (M) parameters by used of Lagrange’s formulation. The second step is implementing the Coriolis and Centrifugal matrix which they can calculate by partial derivatives of kinetic energy. The last step to implement the dynamic equation of robot manipulator is to find the gravity vector by performing the summation of Lagrange’s formulation
The kinetic energy equation (M) is an x n symmetric matrix that can be calculated by the following equation;
M(e) = miJTviJvi + JIC11I1JM1 + m2JTv2U + JtC'/I2Ju2 + m3jT3JT3
+ J TC? I3Jto3 + m4J T 4JT4
+ JLCi^Jm4 + m . J T- J T.
+ JT£l s J Ms +m 6 Jl 6 J T6
+ J LC 6 l 6 J to6
As mentioned above the kinetic energy matrix in n DOF is a n x n matrix that can be calculated by the following matrix [1, 6]
M(q) =
M 11 M 12
M21 -.
M 1„l
M 2n
LM n.1 ............. M nn
The Coriolis matrix (B) is a n X n(n 1) matrix which calculated as follows;
B(q) = b112 b113
b 212
b11n b 123
b21n b 223
b 12n
b1n-1n b2 .n-1n
bn. 12 bn.1.n bn.n-1.n
and the Centrifugal matrix (C) is a n X n matrix;
I" C11 - Gnl (9)
cq =L; : c J LU n1 unnJ
And last the Gravity vector (G) is a n X 1 vector;
G(q) =
9ni
-
2.2 Computed Torque Controller:
The central idea of Computed torque controller (CTC) is feedback linearization so, originally this algorithm is called feedback linearization controller [34-58]. It has assumed that the desired motion trajectory for the manipulator qd (t), as determined, by a path planner. Defines the tracking error as:
e(t) = qd (t) - qa (t)
Where e(t) is error of the plant, q d (t) is desired input variable, that in our system is desired displacement, qa(t) is actual displacement. If an alternative linear state-space equation in the form x = Ax + BU can be defined as
-=is a-+»
With U = -M-1(q). N(q, q) + M-1(q). t and this is known as the Brunousky canonical form. By equation (11) and (12) the Brunousky canonical form can be written in terms of the state x = [eTeT ]T as [1]:
dtie]=is ош+i>
With
U = qd + M 1(q).{N(q.q) - t} (14)
Then compute the required arm torques using inverse of equation (14), is;
t = M(q)(q'd - U) + N(q, q) (15)
This is a nonlinear feedback control law that guarantees tracking of desired trajectory. Selecting proportional-plus-derivative (PD) feedback for U(t) results in the PD-computed torque controller [6];
t = M(q)(qd + Kve + Kpe) + N(q, q) (16)
and the resulting linear error dynamics are
-
(q d + K v e + K p e) = 0 (17)
-
2.3 Fuzzy Logic Technique:
According to the linear system theory, convergence of the tracking error to zero is guaranteed [6]. Where K p and Kv are the controller gains. The result schemes shows in Figure 1, in which two feedback loops, namely, inner loop and outer loop, which an inner loop is a compensate loop and an outer loop is a tracking error loop.
Based on foundation of fuzzy logic methodology; fuzzy logic management has played important rule to design nonlinear management for nonlinear and uncertain systems [16-36].However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of;
Input fuzzification (binary-to-fuzzy [B/F]
conversion), Fuzzy rule base (knowledge base), Inference engine and Output defuzzification (fuzzy-to-binary [F/B] conversion). Figure 2 shows the fuzzy controller part. The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy managements to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. MichioSugeno uses a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base [22-33]
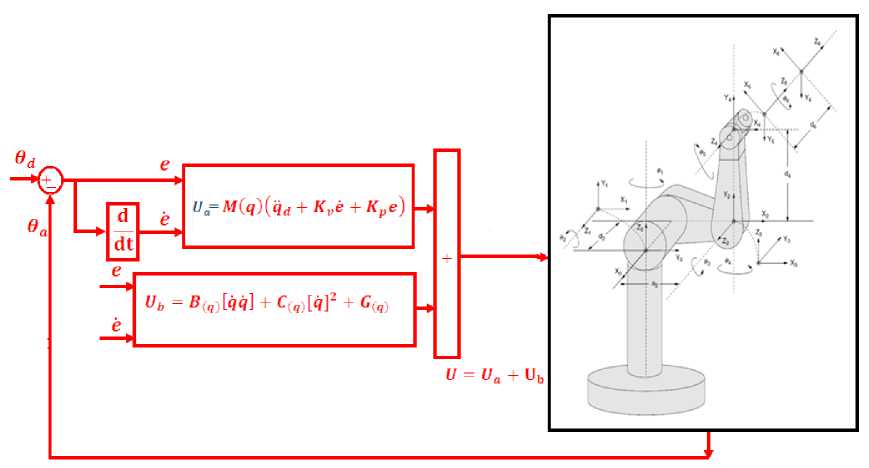
Fig. 1: Block diagram of PD-computed torque controller (PD-CTC)
if xis A and у is В thenz is C 'mamdani' if x is A and у is В thenz is f(x,y) ' sugeno'
When x and у have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation ( AND / OR ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method (COG ) and Centre of area method (COA) are two most common defuzzification methods [41-62].
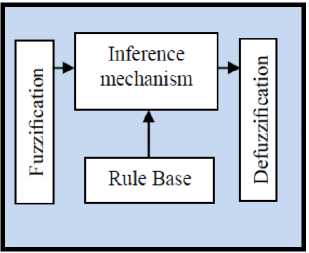
Fig. 2: Fuzzy Controller Part
-
III. Methodol ogy
Computed torque controller (CTC) is an important nonlinear controller in a partly uncertain dynamic system’s parameters. This controller is used in several applications such as in robotics, process control, aerospace and power electronics. Computed torque controller is used to control of nonlinear dynamic systems particularly for robot manipulators, because it has a suitable control performance and it is a robust and stable. Conversely pure computed torque controller is a high-quality nonlinear controller; it has an important problem; nonlinear equivalent dynamic formulation in uncertain dynamic parameter. To compensate the equivalent dynamic problems, this research is focused on applied parallel fuzzy logic theorem in computed torque controller as a compensator. Fuzzy logic theory is used in parallel with computed torque controller to compensate the limited uncertainty in system’s dynamic. In this method fuzzy logic theorem is applied to computed torque controller to remove the nonlinear uncertainty part which it is based on nonlinear dynamic formulation. To achieve this goal, the dynamic equivalent part of pure computed torque controller is modeled by Mamdani’s performance/ error-based fuzzy logic methodology. Another researcher’s method is based on applied fuzzy logic theorem in computed torque controller to design a fuzzy model-based controller. This technique was employed to obtain the desired control behavior with a number of information about dynamic model of system and a fuzzy control was applied to reinforce system performance. Equivalent part of computed torque controller is based on nonlinear dynamic formulations of robot manipulator. Robot manipulator’s dynamic formulations are highly nonlinear and some of parameters are unknown therefore design a controller based on dynamic formulation is complicated. To solve the challenge of computed torque controller based on nonlinear dynamic formulation this research is focused on compensate the nonlinear equivalent formulation by parallel fuzzy logic controller. In this method; dynamic nonlinear equivalent part is modelled by performance/error-based fuzzy logic controller. In this method; error based Mamdani’s fuzzy inference system has considered with two inputs, one output and totally 49 rules. Figure 3 shows error-based parallel fuzzy plus computed torque controller.
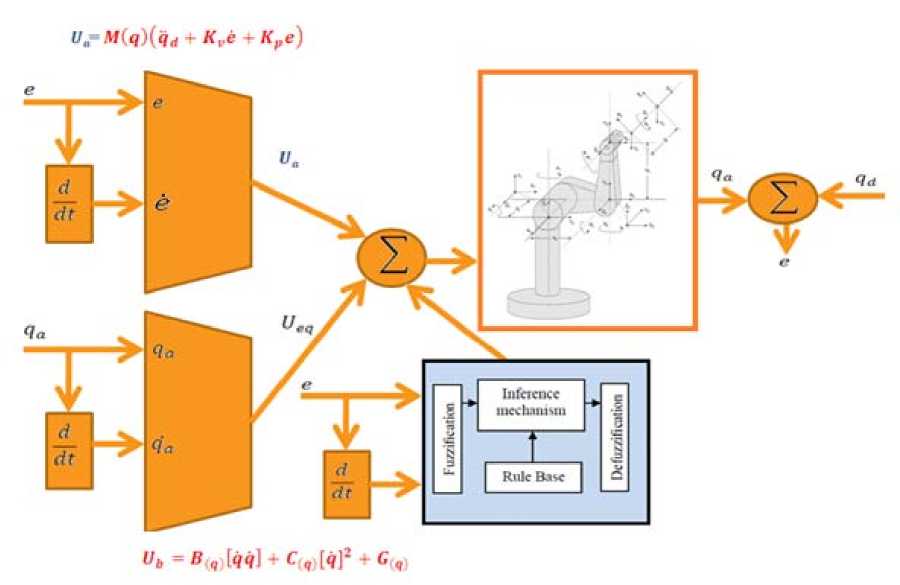
Fig. 3: Block diagram of fuzzy inference system + pure computed torque controller
Based on Figure 3, the parallel fuzzy error-based compensator of computed torque controller’s output is written;
* = Т«ч fuzzy + ^ СТС
Based on fuzzy logic methodology
Л (19)
fto = Ufuzzy = ^ет <(х) i =1
whereетis adjustable parameter (gain updating factor) and C(c)is defined by;
Li^(xi)xi ^bc) =^——— lM
Where ju(xi)is membership functions fuzzy is defined as follows;
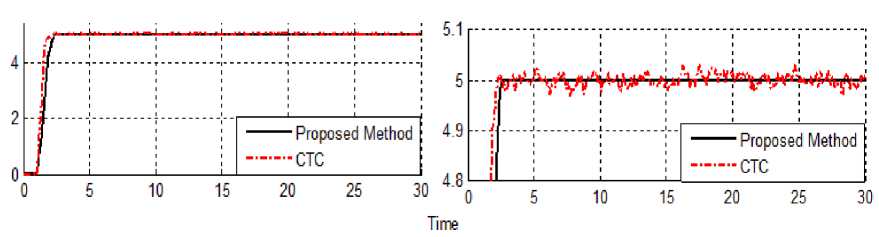
M тfuzzy = ^ ет 1=1 As mentioned in Figure 3, design an error-based parallel fuzzy compensate of equivalent part based on Mamdani’s fuzzy inference method has four steps, namely, fuzzification, fuzzy rule base and rule evaluation, aggregation of the rule output (fuzzy inference system) and defuzzification. Fuzzification: the first step in fuzzification is determine inputs and outputs which, it has two inputs (e, e) and one output (т^и22у ). The inputs are error (e) which measures the difference between desired and actual output position, and the change of error (e) which measures the difference between desired and actual velocity and output is fuzzy equivalent torque. The second step is chosen an appropriate membership function for inputs and output which, to simplicity in implementation because it is a linear function with regard to acceptable performance triangular membership function is selected in this research. The third step is chosen the correct labels for each fuzzy set which, in this research namely as linguistic variable. Based on experience knowledge the linguistic variables for error (e) are; Negative Big (NB), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), Positive Big (PB), and based on literature [40] and experience knowledge it is quantized into thirteen levels represented by: -1, -0.83, -0.66, -0.5, -0.33, -0.16, 0, 0.16, 0.33, 0.5, 0.66, 0.83, 1 the linguistic variables for change of error (e) are; Fast Left (FL), Medium Left (ML), Slow Left (SL),Zero (Z), Slow Right (SR), Medium Right (MR), Fast Right (FR), and it is quantized in to thirteen levels represented by: -6, -5, -0.4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, and the linguistic variables to find the output are; Large Left (LL), Medium Left (ML), Small Left (SL), Zero (Z), Small Right (SR), Medium Right (MR), Large Right (LR) and it is quantized in to thirteen levels represented by: -85, -70.8, -56.7, -42.5, -28.3, -14.2, 0, 14.2, 28.3, 42.5, 56.7, 70.8, 85. Fuzzy rule base and rule evaluation: the first step in rule base and evaluation is to provide a least structured method to derive the fuzzy rule base which, expert experience and control engineering knowledge is used because this method is the least structure of the other one and the researcher derivation the fuzzy rule base from the knowledge of system operate and/or the classical controller. Design the rule base of fuzzy inference system can play important role to design the best performance of parallel fuzzy plus computed torque controller, that to calculate the fuzzy rule base the researcher is used to heuristic method which, it is based on the behavior of the control of robot manipulator. The complete rule base for this controller is shown in Table 1. Rule evaluation focuses on operation in the antecedent of the fuzzy rules in fuzzy computed torque controller. This part is used AND /OR fuzzy operation in antecedent part which AND operation is used. Aggregation of the rule output (Fuzzy inference): based onfuzzy methodology, Max-Min aggregation is used in this work. Table 1: Modified Fuzzy rule base table Decrease the overshoot ё ------------► ex FL ML SL Z SR MR FR 1 e In NB LL LL LL ML SL SL Z NM LL ML ML ML SL Z SR NS LL ML SL SL Z SR MR Z LL ML SL Z SR MR LR OJ A JZ In Q PS ML SL Z SR SR MR LR PM SL Z SR MR MR MR LR PB Z SR SR MR LR LR LR Defuzzification: The last step to design fuzzy inference in our parallel fuzzy compensator plus computed torque controller is defuzzification. This part is used to transform fuzzy set to crisp set, therefore the input for defuzzification is the aggregate output and the output of it is a crisp number. Based on fuzzy methodology Center of gravity method (COG) is used in this research. Table 2 shows the lookup table in parallel fuzzy compensator computed torque controller which is computed by COG defuzzification method. Table 2 has 169 cells to shows the error-based fuzzy compensate of equivalent part behavior. Table 2: г fuzzy performance: lookup table in parallel fuzzy compensate of computed torque controller by COG e__ Membership Function (t fllZZy) I e -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -1 -85 -84.8 -84.8 -84 -82.1 -81 -79 -71 -68 -65 -62 -60 -54 -0.83 -84.8 -84 -82 -80 -78 -77 -74 -70 -64 -60 -56 -54 -47 -0.66 -78 -73 -70 -68 -64 -61 -60 -57 -55 -50 -47 -40 -38 -0.5 -70 -60 -58 -51 -42 -38 -34 -33 -31 -29 -28.4 -28.1 -28 -0.33 -50 -48 -45 -40 -38 -34 -32 -30 -28 -26 -25 -21 -20 -0.16 -30 -25 -21 -18 -16 -14 -10 -9 -8 -7 -6.8 -6 -5 0 -10 -8 -6 -1 2 3 6 7 8 10 12 15 17 0.16 15 18 21 22 23 25 27 28 29 30 30.5 30.8 31 0.33 29 29.8 31 33 34 34.6 35 35.2 36 37 38 39 42 0.5 40 41 42 43 45 45 46 46.3 46.8 47 48 51 52 0.66 48 49 50 52 53 55 56 57 58 59 60 61 63 0.83 60 61 62 63 64 66 67 68 68.5 69 70 70.8 71 1 66 68.7 68.9 70 72 74 75 77 78 79 81 83 84 IV. Results and Discussion In this section, we use a benchmark model, robot manipulator, to evaluate our control algorithms. We compare the following managements: PD computed torque controller and parallel fuzzy inference compensator plus computed torque controller which is proposed method in this paper. The simulation was implemented in MATLAB/SIMULINK environment. Close loop response of robot manipulator trajectory planning: Figure 4 illustrates the tracking performance in these controllers. Based on Figure 4; pure PD controller has a slight oscillation in all links, because robot is a highly nonlinear system and control of this system by pure nonlinear method is very difficult. Fig. 4: Pure CTC and Proposed method trajectory following without disturbance Close loop response of trajectory planning in presence of disturbance: Figure 5 demonstrates the power disturbance elimination in these controllers in presence of disturbance for robot. The disturbance rejection is used to test the robustness. Fig. 5: Pure CTC and Proposed method trajectory following with disturbance Based on Figure 5; by comparison between CTC and proposed method, proposed methodology is more stable V. Conclusion The main contribution of this paper is compensating the nonlinear model base controller by nonlinear artificial intelligence model-free compensator. The structure of computed torque controller with parallel fuzzy inference compensator is new. We propose parallel structure compensator to reduce the error and increase the stability. The key technique is dead-zone, such that fuzzy inference compensator and sliding mode control can be switched automatically. Based on proposed methodology, artificial parallel fuzzy inference system is used to compensate the uncertainty in model-base nonlinear controller. Acknowledgment The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Research and Development Corporation Program of Iran under grant no. 2012-Persian Gulf-1A. and robustness than pure nonlinear controller.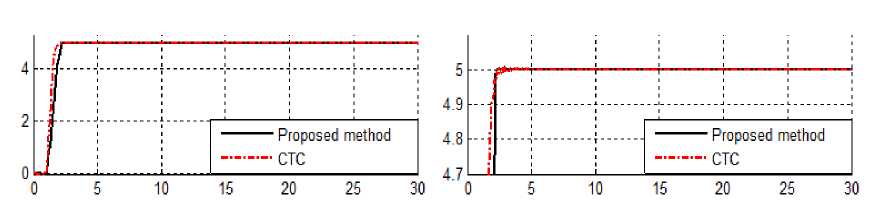
Список литературы Design Computed Torque Controller with Parallel Fuzzy Inference System Compensator to Control of Robot Manipulator
- G. Robinson, and J. Davies, “Continuum robots – a state of the art,”Proc. IEEE International Conference on Robotics and Automation, Detroit, MI, 1999, vol. 4, pp. 2849-2854.
- I.D. Walker, D. Dawson, T. Flash, F. Grasso, R. Hanlon, B. Hochner, W.M. Kier, C. Pagano,C.D. Rahn, Q. Zhang, “Continuum Robot Arms Inspired by Cephalopods, Proceedings SPIE Conference on Unmanned Ground Vehicle Technology VII, Orlando, FL, pp 303-314, 2005.
- K. Suzumori, S. Iikura, and H. Tanaka, “Development of Flexible Microactuator and it’s Applications to Robotic Mechanisms”, Proceedings IEEE International Conference on Robotics and Automation, Sacramento, California, pp. 1622-1627, 1991.
- D. Trivedi, C.D. Rahn, W.M. Kier, and I.D. Walker, “Soft Robotics: Biological Inspiration, State of the Art, and Future Research”, Applied Bionics and Biomechanics, 5(2), pp. 99-117, 2008.
- W. McMahan, M. Pritts, V. Chitrakaran, D. Dienno, M. Grissom, B. Jones, M. Csencsits, C.D. Rahn, D. Dawson, and I.D. Walker, “Field Trials and Testing of “OCTARM” Continuum Robots”, Proc. IEEE International Conference on Robotics and Automation, pp. 2336-2341, 2006.
- W. McMahan, I.D. Walker, “Octopus-Inspired Grasp Synergies for Continuum Manipulators”, Proc. IEEE International Conference on Robotics and Biomimetics, pp. 945- 950, 2009.
- I. Boiko, L. Fridman, A. Pisano and E. Usai, "Analysis of chattering in systems with second-order sliding modes," IEEE Transactions on Automatic Control, No. 11, vol. 52,pp. 2085-2102, 2007.
- J. Wang, A. Rad and P. Chan, "Indirect adaptive fuzzy sliding mode control: Part I: fuzzy switching," Fuzzy Sets and Systems, No. 1, vol. 122,pp. 21-30, 2001.
- J. J. E. Slotine, "Sliding controller design for non-linear systems," International Journal of Control, No. 2, vol. 40, pp. 421-434, 1984.
- R. Palm, "Sliding mode fuzzy control," IEEE conference proceeding,2002, pp. 519-526.
- H. Elmali and N. Olgac, "Implementation of sliding mode control with perturbation estimation (SMCPE)," Control Systems Technology, IEEE Transactions on, No. 1, vol. 4, pp. 79-85, 2002.
- J. Moura and N. Olgac, "A comparative study on simulations vs. experiments of SMCPE," IEEE conference proceeding, 2002, pp. 996-1000.
- Y. Li and Q. Xu, "Adaptive Sliding Mode Control With Perturbation Estimation and PID Sliding Surface for Motion Tracking of a Piezo-Driven Micromanipulator," Control Systems Technology, IEEE Transactions on, No. 4, vol. 18, pp. 798-810, 2010.
- Farzin Piltan, M. Akbari, M. Piran , M. Bazregar. ”Design Model Free Switching Gain Scheduling Baseline Controller with Application to Automotive Engine”, International Journal of Information Technology and Computer Science, 01:65-73, 2013.
- Farzin Piltan , N. Sulaiman, Zahra Tajpaykar, Payman Ferdosali, Mehdi Rashidi, “Design Artificial Nonlinear Robust Controller Based on CTLC and FSMC with Tunable Gain,” International Journal of Robotic and Automation, 2 (3): 205-220, 2011.
- Farzin Piltan, A. R. Salehi and Nasri B Sulaiman.,” Design artificial robust control of second order system based on adaptive fuzzy gain scheduling,” world applied science journal (WASJ), 13 (5): 1085-1092, 2011.
- Farzin Piltan, N. Sulaiman, Atefeh Gavahian, Samira Soltani, Samaneh Roosta, “Design Mathematical Tunable Gain PID-Like Sliding Mode Fuzzy Controller with Minimum Rule Base,” International Journal of Robotic and Automation, 2 (3): 146-156, 2011.
- Farzin Piltan , A. Zare, Nasri B. Sulaiman, M. H. Marhaban and R. Ramli, , “A Model Free Robust Sliding Surface Slope Adjustment in Sliding Mode Control for Robot Manipulator,” World Applied Science Journal, 12 (12): 2330-2336, 2011.
- Farzin Piltan , A. H. Aryanfar, Nasri B. Sulaiman, M. H. Marhaban and R. Ramli “Design Adaptive Fuzzy Robust Controllers for Robot Manipulator,” World Applied Science Journal, 12 (12): 2317-2329, 2011.
- Farzin Piltan, N. Sulaiman , Arash Zargari, Mohammad Keshavarz, Ali Badri , “Design PID-Like Fuzzy Controller With Minimum Rule Base and Mathematical Proposed On-line Tunable Gain: Applied to Robot Manipulator,” International Journal of Artificial intelligence and expert system, 2 (4):184-195, 2011.
- Farzin Piltan, Nasri Sulaiman, M. H. Marhaban and R. Ramli, “Design On-Line Tunable Gain Artificial Nonlinear Controller,” Journal of Advances In Computer Research, 2 (4): 75-83, 2011.
- Farzin Piltan, N. Sulaiman, Payman Ferdosali, Iraj Assadi Talooki, “ Design Model Free Fuzzy Sliding Mode Control: Applied to Internal Combustion Engine,” International Journal of Engineering, 5 (4):302-312, 2011.
- Farzin Piltan, N. Sulaiman, Samaneh Roosta, M.H. Marhaban, R. Ramli, “Design a New Sliding Mode Adaptive Hybrid Fuzzy Controller,” Journal of Advanced Science & Engineering Research , 1 (1): 115-123, 2011.
- Farzin Piltan, Atefe Gavahian, N. Sulaiman, M.H. Marhaban, R. Ramli, “Novel Sliding Mode Controller for robot manipulator using FPGA,” Journal of Advanced Science & Engineering Research, 1 (1): 1-22, 2011.
- Farzin Piltan, N. Sulaiman, A. Jalali & F. Danesh Narouei, “Design of Model Free Adaptive Fuzzy Computed Torque Controller: Applied to Nonlinear Second Order System,” International Journal of Robotics and Automation, 2 (4):232-244, 2011.
- Farzin Piltan, N. Sulaiman, Iraj Asadi Talooki, Payman Ferdosali, “Control of IC Engine: Design a Novel MIMO Fuzzy Backstepping Adaptive Based Fuzzy Estimator Variable Structure Control ,” International Journal of Robotics and Automation, 2 (5):360-380, 2011.
- Farzin Piltan, N. Sulaiman, Payman Ferdosali, Mehdi Rashidi, Zahra Tajpeikar, “Adaptive MIMO Fuzzy Compensate Fuzzy Sliding Mode Algorithm: Applied to Second Order Nonlinear System,” International Journal of Engineering, 5 (5): 380-398, 2011.
- Farzin Piltan, N. Sulaiman, Hajar Nasiri, Sadeq Allahdadi, Mohammad A. Bairami, “Novel Robot Manipulator Adaptive Artificial Control: Design a Novel SISO Adaptive Fuzzy Sliding Algorithm Inverse Dynamic Like Method,” International Journal of Engineering, 5 (5): 399-418, 2011.
- Farzin Piltan, N. Sulaiman, Sadeq Allahdadi, Mohammadali Dialame, Abbas Zare, “Position Control of Robot Manipulator: Design a Novel SISO Adaptive Sliding Mode Fuzzy PD Fuzzy Sliding Mode Control,” International Journal of Artificial intelligence and Expert System, 2 (5):208-228, 2011.
- Farzin Piltan, SH. Tayebi HAGHIGHI, N. Sulaiman, Iman Nazari, Sobhan Siamak, “Artificial Control of PUMA Robot Manipulator: A-Review of Fuzzy Inference Engine And Application to Classical Controller ,” International Journal of Robotics and Automation, 2 (5):401-425, 2011.
- Farzin Piltan, N. Sulaiman, Abbas Zare, Sadeq Allahdadi, Mohammadali Dialame, “Design Adaptive Fuzzy Inference Sliding Mode Algorithm: Applied to Robot Arm,” International Journal of Robotics and Automation , 2 (5): 283-297, 2011.
- Farzin Piltan, Amin Jalali, N. Sulaiman, Atefeh Gavahian, Sobhan Siamak, “Novel Artificial Control of Nonlinear Uncertain System: Design a Novel Modified PSO SISO Lyapunov Based Fuzzy Sliding Mode Algorithm ,” International Journal of Robotics and Automation, 2 (5): 298-316, 2011.
- Farzin Piltan, N. Sulaiman, Amin Jalali, Koorosh Aslansefat, “Evolutionary Design of Mathematical tunable FPGA Based MIMO Fuzzy Estimator Sliding Mode Based Lyapunov Algorithm: Applied to Robot Manipulator,” International Journal of Robotics and Automation, 2 (5):317-343, 2011.
- Farzin Piltan, N. Sulaiman, Samaneh Roosta, Atefeh Gavahian, Samira Soltani, “Evolutionary Design of Backstepping Artificial Sliding Mode Based Position Algorithm: Applied to Robot Manipulator,” International Journal of Engineering, 5 (5):419-434, 2011.
- Farzin Piltan,N. Sulaiman, S.Soltani, M. H. Marhaban&R. Ramli, “An Adaptive sliding surface slope adjustment in PD Sliding Mode Fuzzy Control for Robot Manipulator,” International Journal of Control and Automation , 4 (3): 65-76, 2011.
- Farzin Piltan, N. Sulaiman, Mehdi Rashidi, Zahra Tajpaikar, Payman Ferdosali, “Design and Implementation of Sliding Mode Algorithm: Applied to Robot Manipulator-A Review ,” International Journal of Robotics and Automation, 2 (5):265-282, 2011.
- Farzin Piltan, N. Sulaiman, Amin Jalali, Sobhan Siamak, and Iman Nazari, “Control of Robot Manipulator: Design a Novel Tuning MIMO Fuzzy Backstepping Adaptive Based Fuzzy Estimator Variable Structure Control ,” International Journal of Control and Automation, 4 (4):91-110, 2011.
- Farzin Piltan, N. Sulaiman, Atefeh Gavahian, Samaneh Roosta, Samira Soltani, “On line Tuning Premise and Consequence FIS: Design Fuzzy Adaptive Fuzzy Sliding Mode Controller Based on Lyaponuv Theory,” International Journal of Robotics and Automation, 2 (5):381-400, 2011.
- Farzin Piltan, N. Sulaiman, Samaneh Roosta, Atefeh Gavahian, Samira Soltani, “Artificial Chattering Free on-line Fuzzy Sliding Mode Algorithm for Uncertain System: Applied in Robot Manipulator,” International Journal of Engineering, 5 (5):360-379, 2011.
- Farzin Piltan,N. Sulaiman and I.AsadiTalooki, “Evolutionary Design on-line Sliding Fuzzy Gain Scheduling Sliding Mode Algorithm: Applied to Internal Combustion Engine,” International Journal of Engineering Science and Technology, 3 (10):7301-7308, 2011.
- Farzin Piltan, Nasri B Sulaiman, Iraj Asadi Talooki and Payman Ferdosali.,” Designing On-Line Tunable Gain Fuzzy Sliding Mode Controller Using Sliding Mode Fuzzy Algorithm: Applied to Internal Combustion Engine,” world applied science journal (WASJ), 15 (3): 422-428, 2011.
- Farzin Piltan, N. Sulaiman, M. H. Marhaban, Adel Nowzary, Mostafa Tohidian,” “Design of FPGA based sliding mode controller for robot manipulator,” International Journal of Robotic and Automation, 2 (3): 183-204, 2011.
- Farzin Piltan, B. Boroomand, A. Jahed and H. Rezaie. ”Performance-Based Adaptive Gradient Descent Optimal Coefficient Fuzzy Sliding Mode Methodology”, International Journal of Intelligent Systems and Applications, 11: 40-52 2012.
- Samira Soltani &Farzin Piltan, “Design Artificial Nonlinear Controller Based on Computed Torque like Controller with Tunable Gain”. World Applied Science Journal,14 (9): 1306-1312, 2011.
- Farzin Piltan, H. Rezaie, B. Boroomand, Arman Jahed,” Design robust back stepping online tuning feedback linearization control applied to IC engine,” International Journal of Advance Science and Technology, 42: 183-204, 2012.
- Farzin Piltan, I. Nazari, S. Siamak, P. Ferdosali ,”Methodology of FPGA-based mathematical error-based tuning sliding mode controller” International Journal of Control and Automation, 5(1): 89-110, 2012.
- Farzin Piltan, M. A. Dialame, A. Zare, A. Badri ,”Design Novel Lookup table changed Auto Tuning FSMC: Applied to Robot Manipulator” International Journal of Engineering, 6(1): 25-40, 2012.
- Farzin Piltan, B. Boroomand, A. Jahed, H. Rezaie ,”Methodology of Mathematical Error-Based Tuning Sliding Mode Controller” International Journal of Engineering, 6(2): 96-112, 2012.
- Farzin Piltan, F. Aghayari, M. R. Rashidian, M. Shamsodini, ”A New Estimate Sliding Mode Fuzzy Controller for Robotic Manipulator” International Journal of Robotics and Automation, 3(1): 45-58, 2012.
- Farzin Piltan, M. Keshavarz, A. Badri, A. Zargari , ”Design novel nonlinear controller applied to robot manipulator: design new feedback linearization fuzzy controller with minimum rule base tuning method” International Journal of Robotics and Automation, 3(1): 1-18, 2012.
- Farzin Piltan, A. Jahed, H. Rezaie and B. Boroomand. ” Methodology of Robust Linear On-line High Speed Tuning for Stable Sliding Mode Controller: Applied to Nonlinear System”, International Journal of Control and Automation, 5(3): 217-236, 2012.
- Farzin Piltan, A. Hosainpour, E. Mazlomian, M.Shamsodini, M.H Yarmahmoudi. ”Online Tuning Chattering Free Sliding Mode Fuzzy Control Design: Lyapunov Approach” International Journal of Robotics and Automation, 3(3):77-105, 2012.
- FarzinPiltan, M.H. Yarmahmoudi, M. Shamsodini, E.Mazlomian, A.Hosainpour.” PUMA-560 Robot Manipulator Position Computed Torque Control Methods Using MATLAB/SIMULINK and Their Integration into Graduate Nonlinear Control and MATLAB Courses” International Journal of Robotics and Automation, 3(3):167-191, 2012.
- FarzinPiltan, R. Bayat, F. Aghayari, B. Boroomand. “Design Error-Based Linear Model-Free Evaluation Performance Computed Torque Controller” International Journal of Robotics and Automation, 3(3):151-166, 2012.
- FarzinPiltan, S. Emamzadeh, Z. Hivand, F. Shahriyari& Mina Mirazaei.” PUMA-560 Robot Manipulator Position Sliding Mode Control Methods Using MATLAB/SIMULINK and Their Integration into Graduate/Undergraduate Nonlinear Control, Robotics and MATLAB Courses” International Journal of Robotics and Automation, 3(3): 106-150,2012.
- FarzinPiltan, J. Meigolinedjad, S. Mehrara, S. Rahmdel. ” Evaluation Performance of 2nd Order Nonlinear System: Baseline Control Tunable Gain Sliding Mode Methodology” International Journal of Robotics and Automation, 3(3):192-211, 2012.
- FarzinPiltan, M. Mirzaie, F. Shahriyari, ImanNazari& S. Emamzadeh.” Design Baseline Computed Torque Controller” International Journal of Engineering, 3(3):129-141, 2012.
- FarzinPiltan, MojdehPiran, Mansour Bazregar, Mehdi Akbari " Design High Impact Fuzzy Baseline Variable Structure Methodology to Artificial Adjust Fuel Ratio", International Journal of Intelligent Systems and Applications(IJISA) , 5(2):59-70, 2013.
- Farzin Piltan, M. Akbari, M. Piran, M. Bazrega “Design Model Free Switching Gain Scheduling Baseline Controller with Application to Automotive Engine,” International Journal of Information Technology and Computer Science (IJITCS), 5 (1): 65-76, 2013.
- FARZIN PILTAN, MOHAMMADHOSSAIN YARMAHMOUDI, MINA MIRZAIE, SARA EMAMZADEH, ZAHRA HIVAND”Design Novel Fuzzy Robust Feedback Linearization Control with Application to Robot Manipulator ” International Journal of Intelligent Systems and Applications (IJISA), 5(1): 2013.
- MANSOUR BAZREGAR, FARZIN PILTAN, ALIREZA NABAEE, MOHAMMAD MAHDI EBRAHIMI”Parallel Soft Computing Control Optimization Algorithm for Uncertainty Dynamic Systems” International Journal of Advanced Science and Technology (IJAST), 51(Feb.): 2013.
- FarzinPiltan, ShahnazTayebiHaghighi”Design Gradient Descent Optimal Sliding Mode Control of Continuum Robots” IAES International Journal of Robotics and Automation (IJRA), 1(4): 2013.


