Design Intelligent Model-free Hybrid Guidance Controller for Three Dimension Motor

Published Online October 2014 in MECS

1Research and Development Department, Institute of Advance Science and Technology-IRAN SSP, Shiraz/Iran,

Multi-degree-of-freedom (DOF) actuators are finding wide use in a number of Industries. Currently, a significant number of the existing robotic actuators that can realize multi-DOF motion are constructed using gear and linkages to connect several single-DOF motors in series and/or parallel. Not only do such actuators tend to be large in size and mass, but they also have a decreased positioning accuracy due to mechanical deformation, friction and backlash of the gears and linkages. A number of these systems also exhibit singularities in their workspaces, which makes it virtually impossible to obtain uniform, high-speed, and high-precision motion. For high precession trajectory planning and control, it is necessary to replace the actuator system made up of several singleDOF motors connected in series and/or parallel with a single multi-DOF actuator. The need for such systems has motivated years of research in the development of unusual, yet high performance actuators that have the potential to realize multi-DOF motion in a single joint. One such actuator is the spherical motor. Compared to conventional robotic manipulators that offer the same motion capabilities, the spherical motor possesses several advantages. Not only can the motor combine 3-DOF motion in a single joint, it has a large range of motion with no singularities in its workspace. The spherical motor is much simpler and more compact in design than most multiple single-axis robotic manipulators. The motor is also relatively easy to manufacture. The spherical motor have potential contributions to a wide range of applications such as coordinate measuring, object tracking, material handling, automated assembling, welding, and laser cutting. All these applications require high precision motion and fast dynamic response, which the spherical motor is capable of delivering. Previous research efforts on the spherical motor have demonstrated most of these features. These, however, come with a number of challenges. The spherical motor exhibits coupled, nonlinear and very complex dynamics. The design and implementation of feedback controllers for the motor are complicated by these dynamics. The controller design is further complicated by the orientation-varying torque generated by the spherical motor. Some of these challenges have been the focus of previous and ongoing research [1-5].

Controller (control system) is a device to sense information from linear or nonlinear system (e.g., three degrees of freedom spherical motor) [6-10]. In feedback control system considering that there are many disturbances and also variable dynamic parameters something that is really necessary is keeping plant variables close to the desired value. Feedback control system development is the most important thing in many different fields of safety engineering. The main targets in design control systems are safety stability, good disturbance rejection to reach the best safety, and small tracking error[11-15]. At present, in some applications spherical motors are used in unknown and unstructured environment, therefore strong mathematical tools used in new control methodologies to design nonlinear robust controller with an acceptable safety performance (e.g., minimum error, good trajectory, disturbance rejection). According to the control theory, systems’ controls are divided into two main groups: conventional control theory and soft computing control theory. Conventional control theories are work based on system dynamic model. This technique is highly sensitive to the knowledge of all parameters of nonlinear spherical motor’s dynamic equation. Conventional control theory is divided into two main groups: linear control theory and nonlinear control theory. Soft computing (intelligent) control theory is free of some challenges associated to conventional control theory. This technique is worked based on intelligent control theory. This theory is divided into the following groups: fuzzy logic theory, neural network theory, genetic algorithm and neuro-fuzzy theory.

Although the fuzzy-logic control is not a new technique, its application in this current research is considered to be novel since it aimed for an automated dynamic-less response rather than for the traditional objective of uncertainties compensation[14-15]. The intelligent tracking control using the fuzzy-logic technique provides a cost-and-time efficient control implementation due to the automated dynamic-less input. This in turn would further inspire multi-uncertainties testing for spherical motor. In project we can use fuzzy logic theory when a plant can be considered as a black box with outputs available for measurement and a possibility of changing inputs. The plant is supposed to be observable and controllable. Some information about the plant operation or plant control is available, which can or cannot be of a quantitative nature, but it can be formulated as a set of rules (maybe after some processing). An acceptable fuzzy control solution is possible, which should satisfy design specifications. It must not be optimal in regard to some criteria as it is hard to prove that a fuzzy control system is optimal and even stable. However, a fuzzy controller is able to provide a stable and ‘good’ solution.

This method is based on design minimum rule base Proportional Integral Derivative (PID) Fuzzy hybrid guidance Controller for three dimensions spherical motor is presented in this research. This research has two important objectives: reduce the number of PID fuzzy controller rule base, based on parallel methodology and modify the performance and guidance of fuzzy logic theory based on hybrid theory.

This paper is organized as follows; section 2, is served as an introduction to the dynamic of three degrees of freedom spherical motor, design linear PID controller and fuzzy inference system. Part 3, introduces and describes the methodology algorithm. Section 4 presents the simulation results and discussion of this algorithm applied to three degrees of freedom spherical motor and the final section is described the conclusion.

• II.    Theory

Dynamic and Kinematics Formulation of Spherical Motor: Dynamic modeling of spherical motors is used to describe the behavior of spherical motor such as linear or nonlinear dynamic behavior, design of model based controller such as pure sliding mode controller which design this controller is based on nonlinear dynamic equations, and for simulation. The dynamic modeling describes the relationship between motion, velocity, and accelerations to force/torque or current/voltage and also it can be used to describe the particular dynamic effects (e.g., inertia, coriolios, centrifugal, and the other parameters) to behavior of system[1-10]. Spherical motor has nonlinear and uncertain dynamic parameters 3 degrees of freedom (DOF) motor.

The equation of a spherical motor governed by the following equation [1-10]:

H (q) [д] + B(q) [4] + C(q) [^ ² ] = [^]    (1)

Where τ is actuation torque, H (q) is a symmetric and positive define inertia matrix, B(q) is the matrix of coriolios torques, C(q) is the matrix of centrifugal torques.

This is a decoupled system with simple second order linear differential dynamics. In other words, the component q influences, with a double integrator relationship, only the variable q_t , independently of the motion of the other parts. Therefore, the angular acceleration is found as to be [1-11]:

q =H 4q).{r-{B + C}}        (2)

This technique is very attractive from a control point of view.

Study of spherical motor is classified into two main groups: kinematics and dynamics. Calculate the relationship between rigid bodies and final part without any forces is called Kinematics. Study of this part is pivotal to design with an acceptable performance controller, and in real situations and practical applications. As expected the study of kinematics is divided into two main parts: forward and inverse kinematics. Forward kinematics has been used to find the position and orientation of task frame when angles of joints are known. Inverse kinematics has been used to find possible joints variable (angles) when all position and orientation of task frame be active [1].

The main target in forward kinematics is calculating the following function:

У (X,q ) = 0                   (3)

Where V (.) E Rn is a nonlinear vector function, X = [X1,X2,......, X;|T is the vector of task space variables which generally task frame has three task space variables, three orientation, = — iqq, q2^-.->Пп]Т is a vector of angles or displacement, and finally n is the number of actuated joints. The Denavit-Hartenberg (D-H) convention is a method of drawing spherical motor free body diagrams. Denvit-Hartenberg (D-H) convention study is necessary to calculate forward kinematics in this motor.

A systematic Forward Kinematics solution is the main target of this part. The first step to compute Forward Kinematics (F.K) is finding the standard D-H parameters. The following steps show the systematic derivation of the standard D-H parameters.

• 1.    Locate the spherical motor

• 2.    Label joints

• 3.    Determine joint rotation ( 9 )

• 4.    Setup base coordinate frames.

• 5.    Setup joints coordinate frames.

• 6.    Determine a , , thata , , link twist, is the angle between and     about an .

• 7.    Determine d , and a , , that a , , link length, is the distance between and     along .   , offset, is

• 8.    Fill up the D-H parameters table. The second step to compute Forward kinematics is finding the rotation matrix (R ° ). The rotation matrix from[Fj to {F, _ ₁} is given by the following equation;

the distance between X , _ ₁ and X , along Z , axis.

Ri ~1 = Ui№)VKai)(4)

Where и ,(_е.) is given by the following equation [1-11];

rcos (0,)  -5т(600

ut (9;) = Is т(0,)   oos(9t)   ol

0         01

and V ( _ati is given by the following equation [1-11];

V (_6i) = 0 cos(a)

0 sin(аi)

—s in(a ,) cos (а,)

So (R ° ) is given by [8]

R° = ( UiVi)(U2V2).........M)        (7)

The final step to compute the forward kinematics is calculate the transformation by the following formulation [3]

0_T _ 0_T 1_T 2_T n-l_T _ n ¹      1¹ .2¹ . 3¹ ....... n^{1      [} q

Fuzzy Logic Controller: Based on fuzzy logic methodology; fuzzy logic

0          (8)

foundation of controller has

played important rule to design nonlinear controller for nonlinear and uncertain systems [11-15]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of; Input fuzzification (binary-to-fuzzy [B/F] conversion) Fuzzy rule base (knowledge base), Inference engine and Output defuzzification (fuzzy-to-binary [F/B] conversion). Figure 1 shows fuzzy controller operation.

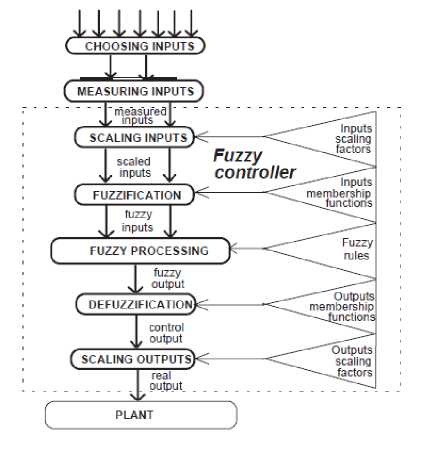
Fig 1: Fuzzy Controller operation

The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy controllers to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno use a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base if x is A and у is В then z is C 'mamdan i'

if x is A and у is В t hen z is f(x,y) 'sugeno'      (9)

When x and y have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation (Л ND / 0 R ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Two most common methods that used in fuzzy logic controllers are Max-min aggregation and Sum-min aggregation. Max-min aggregation defined as below;

The Sum-min aggregation defined as below

И и (х^у^и) =Ц_иг_=1РЙ i(x_k,y_k,U) = Emin^ 1 [^_Дрч(^хк^,Ук^),^_Рт(У⁾]            ⁽¹¹⁾

where г is the number of fuzzy rules activated by x_k and y_k and also Цу- г _FRt(x_k,y_k, U") is a fuzzy interpretation of i — t^ rule. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method ( CO G) and Centre of area method (C O A ) are two most common defuzzification methods, which C O G method used the following equation to calculate the defuzzification

SiS j_{- T} ■ ^ u^ k _k,y k , U i )

kinematic control method always results in a group of individual controllers, each for an active joint of the manipulator. With the independent joint assumption, no a priori knowledge of robot manipulator dynamics is needed in the kinematic controller design, so the complex computation of its dynamics can be avoided and the controller design can be greatly simplified. This is suitable for real-time control applications when powerful processors, which can execute complex algorithms rapidly, are not accessible. However, since joints coupling is neglected, control performance degrades as operating speed increases and a manipulator controlled in this way is only appropriate for relatively slow motion [14]. The fast motion requirement results in even higher dynamic coupling between the various robot joints, which cannot be compensated for by a standard robot controller such as PID [13], and hence model-based control becomes the alternative.

and C O A method used the following equation to calculate the defuzzification

C O A (x _k, y_k) = S ^ut'^U(k^kk,yk,U^ (13) ^Si ^ U ■ ^(кк ,У к ,^1 ⁾

Where COG(x _k ,y _k ) and COA(x_k,y_k) illustrates the crisp value of defuzzification output, U , E U is discrete element of an output of the fuzzy set, ц _и . (x _k ,y _k , U [ ) is the fuzzy set membership function, and r is the number of fuzzy rules.

Design PID Controller: Design of a linear methodology to control of continuum robot manipulator was very straight forward. Since there was an output from the torque model, this means that there would be two inputs into the PID controller. Similarly, the outputs of the controller result from the two control inputs of the torque signal. In a typical PID method, the controller corrects the error between the desired input value and the measured value. Since the actual position is the measured signal. Figure 2 shows linear PID methodology, applied to continuum robot manipulator [15].

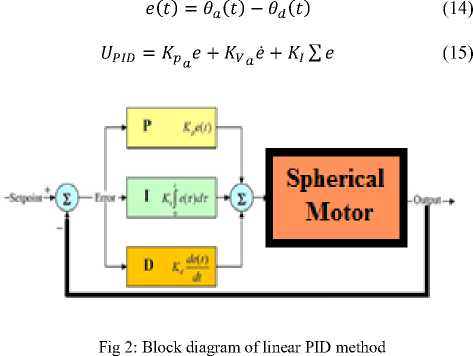
The model-free control strategy is based on the assumption that the joints of the manipulators are all independent and the system can be decoupled into a group of single-axis control systems [15]. Therefore, the

• III.    Methodology

This research focuses on the design two controllers; the first type of controller is PID like fuzzy logic controller based on 49 rule base and the second type of controller is linear PID controller to evaluate the PID like fuzzy controller. Based on previous discussion, fuzzy logic controller is work based on nonlinear dynamic rule bases. However this controller work in many applications but it cannot guarantee reliability and stability. To solve this challenge linear PID controller is used to improve the reliability and stability. Figure 3 Shows the PID like fuzzy hybrid guidance controller for spherical motor.

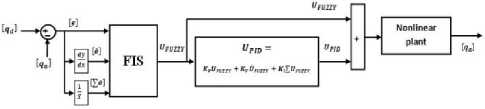
Fig 3: Block diagram of Hybrid Guidance Controller

The formulation of this controller is;

UpiD = KpaUfuZZy + KVaUfUZZy + K, S UfUZZy

Based on fuzzy logic methodology

f(x) = UfUZZy = l,Y=ieT^(x)(17)

where 9^T is adjustable parameter (gain updating factor) and C (x) is defined by;

<(x) = SU(kS

^S t ^U(k t )

Where ц(х , ) is membership function. According to the hybrid control theory;

^T = ^UfuZZy + ^UP1D = ^S^1 6^{T C(x)} + ^[Kp_a^UfuZZy +

^KV _a^UfuZZy + ^K1SU_fu_LZZy]              (19)

One of the main artificial intelligence techniques is fuzzy logic theory. In this theory the behavior and dynamic of controller is defined by rule base. However defined and number of rule base play important role to design high quality controller but system has limitation to the number of rule base to implementation and the speed of response. Based on literature PID controller can reduce or eliminate the steady state error and design stable controller. But this type of controller has three types of inputs; proportional part, integral part and derivative part. To design PID like fuzzy controller and if any input is described with seven linguistic values, and any rule has three conditions we will need 7 × 7 × 7 = 343 rules. It is too much work to write 343 rules, the speed of system is too low and design embedded controller based on FPGA or CPLD is very difficult. Based on (9) the PID controller has three inputs and three coefficients. In PD like fuzzy controller error and change of error are the inputs and if any input is described with seven linguistic values, and any rule has two conditions we will need 7 × 7= 49 rules.

In conventional PI controller error and integral of error are the inputs. The PID-like fuzzy controller can be constructed as a parallel structure of a PD-like fuzzy controller and a conventional PI- controller with the output approximated as:

U_P[D = (^e + K_Vae) -K-^e + K^e) (20)

In this type of design, we have 49 rule bases for PD like fuzzy controller. This PID like fuzzy controller applied to linear PID controller to remove the challenge in this research based on non-classical method and classical method. Figure 4 shows the block diagram of PID like fuzzy hybrid guidance controller.

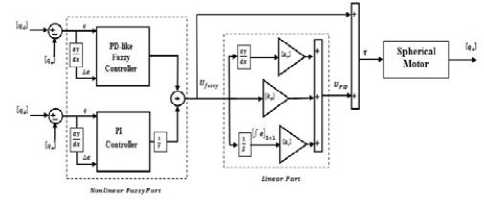
Fig 4: Block diagram of PID like Fuzzy Hybrid Guidance Controller

• IV.    Results And Discussion

PID like fuzzy hybrid guidance controller was tested to Step response trajectory. In this simulation is used to control position of spherical motor without and with external disturbance. The simulation was implemented in MATLAB/SIMULINK environment. These systems are tested by band limited white noise with a predefined 40% of relative to the input signal amplitude. This type of noise is used to external disturbance in continuous and hybrid systems and applied to nonlinear dynamic of these controllers.

Tracking performances: stability and robust are two main important experiments under condition of certain and uncertain parameters. To test the stability, trajectory following is introduced. This part focuses on comparison between conventional PID control and PID like fuzzy hybrid guidance controller. Based on Fig 5, pure PID controller has a slight transient oscillation and overshoot, to solve this challenge hybrid guidance method is used also in proposed method the output gain updating factor must changed. In this design pure PID controller has about 2% overshoot but these two controller have the same rise time.

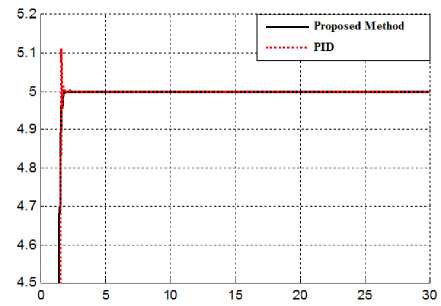
Fig 5: PID controller and proposed method

Disturbance rejection: this test is used to robust checking of controllers. Figure 6 shows the power disturbance elimination in proposed method and pure PID controller in presence of external disturbance and uncertainty parameters. The disturbance rejection is used to test and analyzed the robustness comparisons of these controllers for step trajectory. A band limited white noise with predefined of 40% the power of input signal value is applied to the step trajectory. According to the following graph, pure PID has moderate fluctuations in presence of external disturbance and uncertainty because this type of controller is linear and linear controller cannot guarantee the response of complex system (e.g., spherical motor) especially under condition of uncertainty and external disturbance.

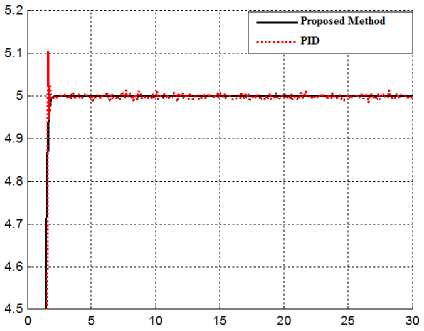
Fig 6: PID controller and proposed method in presence of external disturbance

To eliminate above challenges, decrease the output scaling factor of the PID-part, increase the scaling factor for an integral input compared to other inputs, apply the centre of gravity defuzzification method, reduce the width of the membership function for the zero class of the error signal and Redistribute the membership functions, increasing their concentration around the zero point are offer.

• V.    Conclusion

The central issues and challenges of nonlinear control and estimation problems are to satisfy the desired performance objectives in the presence of noises, disturbances, parameter perturbations, un-modeled dynamics, sensor failures, actuator failures and time delays. Evaluation algorithm proposed controller has shown growing popularity in both industry and academia. To improve the optimality and robustness, we have proposed PD like fuzzy controller parallel with PI controller based on 49 rule base for nonlinear systems with general performance criteria. Fuzzy controller provides us an effective tool to control nonlinear systems through the dynamic formulation of nonlinear system. Fuzzy logic controller is used to estimate highly nonlinear dynamic parameters. Mixed performance criteria have been used to design the controller and the relative weighting matrices of these criteria can be achieved by choosing different coefficient matrices. The simulation studies show that the proposed method provides a satisfactory alternative to the existing nonlinear control approaches.

Acknowledgment

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Institute of Advance Science and Technology Program of Iran under grant no. 2013-Persian Gulf-2A.