Design Intelligent Robust Back stepping Controller

Published Online January 2014 in MECS DOI: 10.5815/ijmecs.2014.01.06

Zahra Esmaieli, Farzin Piltan, Meysam Kazeminasab, Ali Reza Salehi, Mahdi Mirshekaran Institute of Advance Science and Technology, Intelligent control and Robotics Lab. IRAN SSP, Shiraz/Iran,

Controller (control system) is a device which can sense information from linear or nonlinear system (e.g., robot arm) to improve the systems performance and the immune system behavior [1-10]. In feedback control system considering that there are many disturbances and also variable dynamic parameters something that is really necessary is keeping plant variables close to the desired value. Feedback control system development is the most important thing in many different fields of safety engineering. The main targets in design control systems are safety stability, good disturbance rejection to reach the best safety, and small tracking error[11-20]. At present, in some applications robot arms are used in unknown and unstructured environment, therefore strong mathematical tools used in new control methodologies to design nonlinear robust controller with an acceptable safety performance (e.g., minimum error, good trajectory, disturbance rejection). Advanced control techniques such as sliding mode controller, feedback linearization methodology, adaptive and robust have been applied to the control of numerous single- axis machines and robotic manipulators. Since available control techniques for continuum robot and robotic manipulators are so broad, the review in this research is restricted to some of the nonlinear control techniques for continuum robot. Most of the authors referenced on the nonlinear control techniques for continuum robot also do a significant amount of work on the control of robotic manipulators.

In recent years, artificial intelligence theory has been used in nonlinear control systems. Neural network, fuzzy logic, and neuro-fuzzy are synergically combined with nonlinear classical controller and used in nonlinear, time variant, and uncertainty plant (e.g., robot manipulator). Fuzzy logic controller (FLC) is one of the most important applications of fuzzy logic theory. This controller can be used to control nonlinear, uncertain, and noisy systems. This method is free of some modelbased techniques as in classical controllers. As mentioned that fuzzy logic application is not only limited to the modeling of nonlinear systems [21-32]but also this method can help engineers to design easier controller. Control robot arm manipulators using classical controllers are based on manipulator dynamic model. These controllers often have many problems for modelling. Conventional controllers require accurate information of dynamic model of robot manipulator, but these models are multi-input, multi-output and nonlinear and calculate accurate model can be very difficult. When the system model is unknown or when it is known but complicated, it is difficult or impossible to use classical mathematics to process this model[32]. The main reasons to use fuzzy logic technology are able to give approximate recommended solution for unclear and complicated systems to easy understanding and flexible. Fuzzy logic provides a method which is able to model a controller for nonlinear plant with a set of IF-THEN rules, or it can identify the control actions and describe them by using fuzzy rules. It should be mentioned that application of fuzzy logic is not limited to a system that’s difficult for modeling, but it can be used in clear systems that have complicated mathematics models because most of the time it can be shortened in design but there is no high quality design just sometimes we can find design with high quality. Besides using fuzzy logic in the main controller of a control loop, it can be used to design adaptive control, tuning parameters, working in a parallel with the classical and non-classical control method [32-48]. The applications of artificial intelligence such as neural networks and fuzzy logic in modelling and control are significantly growing especially in recent years. For instance, the applications of artificial intelligence, neural networks and fuzzy logic, on robot arm control have reported in [48-55].

Continuum robots represent a class of robots that have a biologically inspired form characterized by flexible backbones and high degrees-of-freedom structures [1]. Theoretically, the compliant nature of a continuum robot provides infinite degrees of freedom to these devices. However, there is a limitation set by the practical inability to incorporate infinite actuators in the device. Most of these robots are consequently under actuated (in terms of numbers of independent actuators) with respect to their anticipated tasks. In other words they must achieve a wide range of configurations with relatively few control inputs. This is partly due to the desire to keep the body structures (which, unlike in conventional rigid-link manipulators or fingers, are required to directly contact the environment) “clean and soft”, but also to exploit the extra control authority available due to the continuum contact conditions with a minimum number of actuators. For example, the Octarm VI continuum manipulator, discussed frequently in this paper, has nine independent actuated degrees-of-freedom with only three sections. Continuum manipulators differ fundamentally from rigid-link and hyper-redundant robots by having an unconventional structure that lacks links and joints. Hence, standard techniques like the Denavit-Hartenberg (D-H) algorithm cannot be directly applied for developing continuum arm kinematics. Moreover, the design of each continuum arm varies with respect to the flexible backbone present in the system, the positioning, type and number of actuators. The constraints imposed by these factors make the set of reachable configurations and nature of movements unique to every continuum robot. This makes it difficult to formulate generalized kinematic or dynamic models for continuum robot hardware. Thus, the kinematics (i.e. geometry based modeling) of a quite general set of prototypes of continuum manipulators has been developed and basic control strategies now exist based on these. The development of analytical models to analyze continuum arm dynamics (i.e. physics based models involving forces in addition to geometry) is an active, ongoing research topic in this field. From a practical perspective, the modeling approaches currently available in the literature prove to be very complicated and a dynamic model which could be conveniently implemented in an actual device’s real-time controller has not been developed yet. The absence of a computationally tractable dynamic model for these robots also prevents the study of interaction of external forces and the impact of collisions on these continuum structures. This impedes the study and ultimate usage of continuum robots in various practical applications like grasping and manipulation, where impulsive dynamics [1-10] are important factors. Although continuum robotics is an interesting subclass of robotics with promising applications for the future, from the current state of the literature, this field is still in its stages of inception.

This paper is organized as follows; section 2, is served as an introduction to the feedback back stepping controller formulation algorithm and its application to control of continuum robot and dynamic of continuum robot. Part 3, introduces and describes the methodology. Section 4 presents the simulation results and discussion of this algorithm applied to a continuum robot and the final section is describing the conclusion.

• II.    THEORY

Dynamic Formulation of Continuum Robot: The Continuum section analytical model developed here consists of three modules stacked together in series. In general, the model will be a more precise replication of the behavior of a continuum arm with a greater of modules included in series. However, we will show that three modules effectively represent the dynamic behavior of the hardware, so more complex models are not motivated. Thus, the constant curvature bend exhibited by the section is incorporated inherently within the model. The model resulting from the application of Lagrange’s equations of motion obtained for this system can be represented in the form

Fcoeff 1 = .q/ ̈+c.q/ ̇+g.q / (1)

where T is a vector of input forces and q is a vector of generalized co-ordinates. The force coefficient matrix Fcoeff transforms the input forces to the generalized forces and torques in the system. The inertia matrix, D is composed of four block matrices. The block matrices that correspond to pure linear accelerations and pure angular accelerations in the system (on the top left and on the bottom right) are symmetric. The matrix c contains coefficients of the first order derivatives of the generalized co-ordinates. Since the system is nonlinear, many elements of c contain first order derivatives of the generalized co-ordinates. The remaining terms in the dynamic equations resulting from gravitational potential energies and spring energies are collected in the matrix G . The coefficient matrices of the dynamic equations are given below,

Fcoeff = (2) (61) (61) (61 + e₂) (6i + e₂ )

⎢ 0 0 1 1 cos ( e₂ ) ( e₂ )⎥ ^⎢0 0 0 0 1 1 ^{⎥ ⎢} ⁄2 - ⁄2 1⁄2 - ⁄2 1⁄2+ s₂sin (e₂)- ⁄2+ s₂sin (e₂)⎥ ⎢0 0 1^⁄2 - ^⁄2 1^⁄2 - ^⁄2 ⎥ ⎣0 0 0 0 1⁄2 - ⁄2 ⎦

D. 1 /= ⎡     mi + m2 ⎢+ m3	m2cos (01) + m3cos ( 9i)	m3cos (01 + 02)	- m2s2sin (01) - m3s2sin (01) - m3s3sin (01 + ^2)	- m3s3sin (01 + 02)	0⎤	(3) ⎥⎥ ⎥
⎢     m2cos (01) ⎢+ m3cos (01)	m2 + m3	m3cos (02)	- m3s3sin ( e2 )	- m3s3sin (^2 )	0	⎥⎥
⎢ m3cos (01 + 02)	m3cos (02)	m3	m3s3sin (02)	0	0	⎥⎥
⎢ ⎢- m2s2sin (01) ⎢- m3s2sin (01) ⎢- m3s3sin (01 + 02)	- m3s3sin (02)	m3s2sin ( 02 )	m2s2 + 71 + Z2 + ^3 + m3s| + m3si + 2m3s3cos ( 02 )S2	^2 + m3si + /3 + m3s3cos (02 )S2		⎥⎥ ⎥⎥
⎢ ⎢- m3s3sin (01 + ^2) ⎢	- m3s3sin (02)	0	^2 + m3si + /3 + m3s3cos ( 92 ) s27	^2 + m3S3 + /3	13	⎥ ⎥⎥ ⎥
⎣          0	0	0	/3	/3	la ⎦

c. 4 /= ⎡ ⎢⎢ ⎢ C11 + C21 ⎢ ⎢ ⎢⎢	- 2m2stn (0i) ̇ - 2m3stn (0i ) ̇	- 2m3stn ( ®1 + ^2) ( ̇1+ ̇2)	- m2s2 cos (01)( ̇ 1) +(1⁄2)(C11 + C21) - m3s2 cos (01)( ̇ 1) -m3S3 cos (01 + 02)( ̇ !)	- m3s3sin (01 + 02)	⎤	(4) ⎥⎥ ⎥⎥
⎢ ⎢ ⎢ 0 ⎢ ⎢ ⎢⎢	c12 + C22	- 2m3sin ( e2 ) ( ̇1+ ̇2)	- m3s3 ( ̇1) +(1⁄2) (c12 + C22) - m3s2 ( ̇1) -m3S3 cos ( 02 )( ̇ 1)	-2m3s3 COS ( 02 )( ̇ 1) - m3s3 cos ( 02 )( ̇ 2)		⎥ ⎥⎥
⎢ ⎢ ⎢ ° ⎢⎢	2m3sin ( 02 )( ̇ 1)	c13 + c23	- m3s3s2 cos ( 02 )( ̇ 1) - m3s3 ( ̇1)	-2m3s3 ( ̇1) - m3s3 ( ̇ 2 )	(⁄) (c13 + c23)	⎥ ⎥⎥
⎢ ⎢(1⁄2) ⎢(cn + C21)	2m3s3cos(02)( ̇ 1) -2m3s2 ( ̇1) + 2m2s2 ( ̇!)	2m3s3(6̇ +6̇2) -2m3s2cos(02) ( 6 ̇ +6̇2)	2m3s3s2 sin ( 02 )( ̇ 2) +(I2 ⁄4) (cn + C21)	m3s3s2 sin (02)( ̇ 2)	°	⎥ ⎥⎥
⎢⎢ ⎢⎢           0	(1⁄2)(C12 + C22)+ 2m3s3cos(02)( ̇ 1)	2m3s3 (6̇ +6̇2)	m3s3s2 sin ( 02 )( ̇ 1)	(I2 ⁄4) (c12 + C22)	0	⎥⎥ ⎥⎥
⎢ ⎣⎢       0	0	(1⁄2)(C13 - c23)	0	0	( I2 ⁄4) (C13 + c23)	⎥ ⎥

• ^G. 1 /=

• ^- m_Ag - m₂g + kn (Si+( ⁄ )01 - $01)+k₂i (Si-( ⁄ )01 - $01)- m₃g

⎡

⎢^- m₂gcos (01)+ki2 (S2+( ⁄ ) 0₂ - ^s02)+fc₂2 (S2-( ⁄ ) 02 - ^s02)- m₃gcos (0i)

⎢- m₃gcos (0i + 0₂)+^13 (S3+( ⁄ ) 03 - ^s03)+^23 (S3-( ⁄ ) 03 - ^s03)

⎢

^⎢ m₂s₂gsin (01)+ m₃s₃gsin (0i + ^2)+ m₃s₂gsin (0i)+кц (Si+( ⁄ )01 - s_Oi)( ⁄ )

⎢⎢                            + C21 (Si-( ⁄ )01 - Soi)(- ⁄ )

⎢ m₃s₃gsin (0i + 0₂)+ki2 (S2+( ⁄ ) 02 - S()2)( ⁄ )+fc₂2 (S2-( ⁄ ) 02 - S()2)(- ⁄ )

⎣           ^13 (S3+( ⁄ ) 03 - s03)( ⁄ )+^23 (S3-( ⁄ ) 03 - s03)(- ⁄ )

Backstepping Controller: The continuum robot dynamics in (1) and (2) have the appropriate structure for the so-called backstopping controller design method. With the position error defined as        Z^ = Xd — Xa, all joints will track the desired specified state Xd if the error dynamics are given as follows:

(Z i + [K_p]Z i ) = 0                               (6)

where [Kp] is a positive definite gain matrix. The error dynamics in (6) can be rewritten as:

X 2 = X_d + [K p ]Z i                              (7)

Substitution of (7) into (1) makes the position error dynamics go to zero. Since the state vector %2 is not a control variable, (7) cannot be directly substituted into (1). The expression in (7) is therefore defined as a fictitious control input and expressed below as XZd/ x2d = X^ + [Kp](Xd — Xa)                   (8)

The fictitious control input in (8) is selected as the specified velocity trajectory and hence the velocity error can be defined as Z7 = X7, — X7  . With the z      zd     za following dynamics

(Z 2 + [K p ]Z 2 ) = 0                               (9)

the joint position error will approach zero asymptotically, which will lead to the eventual asymptotic convergence of the joint position error. The error dynamics in (9) can be rewritten as:

X 2 =X_d+ [K p ]Z 2                           (10)

Substitution of (9) into (1) leads to the following expression as the desired stabilizing torque:

T = [Я] (X 2 _d + [K p ]Z 2 ) + C(X_V X 2 )             (11)

The desired torque control input is a nonlinear compensator since it depends on the dynamics of the spherical motor. The time derivative of desired velocity vector is calculated using (9). In terms of the desired state trajectory, and its time derivatives and the position and velocity state variables, the desired torque can be rewritten in following form:

t= [Я]у + C(X 1 ,X₂)                           (12)

Where

У = X i _d + ([K p ] + [K_d])(X i _d — X 1 )               (13)

+ ([K_p][K_d]X d —X a

The back stepping controller developed above is very similar to inverse dynamics control algorithm developed for robotic manipulators. The back stepping controller is ideal from a control point of view as the nonlinear dynamics of the continuum robot are cancelled and replaced by linear subsystems. The drawback of the back stepping controller is that it requires perfect cancellation of the nonlinear continuum robot dynamics. Accurate real time representations of the robot dynamics are difficulty due to uncertainties in the system dynamics resulting from imperfect knowledge of the robot mechanical parameters; existence of unmolded dynamics and dynamic uncertainties due to payloads. The requirement for perfect dynamic cancellation raises sensitivity and robustness issues that are addressed in the design of a robust back stepping controller. Another drawback of the back stepping controller is felt during real-time implementation of the control algorithm. Implementation of the back stepping controller requires the computation of the exact robot dynamics at each sampling time. This computational burden has an effect on the performance of the control algorithm and imposes constraints on the hardware/software architecture of the control system. By only computing the dominant parts of the robot dynamics, this computational burden can be reduced. These drawbacks of the back stepping controller makes it necessary to consider control algorithms that compensate for both model uncertainties and for approximations made during the on-line computation of robot dynamics. The next section provides robust modifications of the back stepping controller described in this section.

Robust Back stepping Control: When there are uncertainties in the spherical motor dynamics due to modeling inaccuracy and computational relaxation, robust controllers are ideal for ensuring system stability. When the system dynamics are completely known, the required torque control vector for the control of the spherical motor is given by (12) and (13). In the presence of modeling uncertainties, a reasonable approximation of the torque control input vector is given by

T d = [Я]у + c (14)

where [Я]and C are estimates of the inertia and coriolis terms in the spherical motor dynamics; and у is given by (12). The uncertainty on the estimates are expressed as

[Я] = [Я] - [Я] (15)

• [C] = [г] — [C] (16)

These uncertainties account for both imperfect modeling and intentional computational simplification. Application of the approximate control vector given by (14) into (10) leads to the following expression for the closed loop dynamics:

W₂ + С = [Й]у + С                    (17)

Since the inertia matrix [H] is symmetric and positive definite, the closed loop dynamics in (17) can be rewritten as х 1 = У — Ч                                   (18)

Where ч = ([/] - [я]- 1 [г])у - [я]-(19)

Substitution of (13) for у in (17) results in the following expression for the closed loop error dynamics.

• *1 + № + [M*1 + И №i = Ч

Defining a new error state vector, i=[*1]

the error dynamics in (19) can be expressed as

^=[FR+[D](x 1 d-y + i])

Where [F] = [[°]   [*]1 and [Я] = [[°]] are block

[]  [][]

matrices of dimensions R ^6X6 and R^XX3 respectively. Since T] is a nonlinear function of the position and velocity state vectors, the system error dynamics in the above equation are nonlinear and coupled. The back stepping controller developed in the previous section cannot guarantee system stability. The Lyapunov direct method is, however, used to design an outer feedback loop on the error dynamics that compensates for the system uncertainty contributed by T].

Fuzzy Inference Engine: This section provides a review about foundation of fuzzy logic based on [15-20]. Supposed that U is the universe of discourse and x is the element of U, therefore, a crisp set can be defined as a set which consists of different elements (%) will all or no membership in a set. A fuzzy set is a set that each element has a membership grade, therefore it can be written by the following definition;

A = {х, Д_Л(х)|х E X); Л E Я                     (23)

Where an element of universe of discourse is %, дл is the membership function (MF) of fuzzy set. The membership function Gn^Qc)) of fuzzy set A must have a value between zero and one. If the membership function ^л (%) value equal to zero or one, this set change to a crisp set but if it has a value between zero and one, it is a fuzzy set. Defining membership function for fuzzy sets has divided into two main groups; namely; numerical and functional method, which in numerical method each number has different degrees of membership function and functional method used standard functions in fuzzy sets. The membership function which is often used in practical applications includes triangular form, trapezoidal form, bell-shaped form, and Gaussian form.

Linguistic variable can open a wide area to use of fuzzy logic theory in many applications (e.g., control and system identification). In a natural artificial language all numbers replaced by words or sentences.

If — te en Rule statements are used to formulate the condition statements in fuzzy logic. A single fuzzy If — tiee n rule can be written by

If x is Л The n у is В (24)

where A and В are the Linguistic values that can be defined by fuzzy set, the - of the part of “ % is A ” is called the antecedent part and the tieen — part of the part of “ y is В ” is called the Consequent or Conclusion part. The antecedent of a fuzzy if-then rule can have multiple parts, which the following rules shows the multiple antecedent rules:

if e is NB and e is ML then T is LL (25)

where e is error, e is change of error, MB is Negative Big, ML is Medium Left, T is torque and LL is Large Left. - e rules have three parts, namely, fuzzify inputs, apply fuzzy operator and apply implication method which in fuzzify inputs the fuzzy statements in the antecedent replaced by the degree of membership, apply fuzzy operator used when the antecedent has multiple parts and replaced by single number between 0 to 1, this part is a degree of support for the fuzzy rule, and apply implication method used in consequent of fuzzy rule to replaced by the degree of membership. The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy controllers to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno uses a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base

Mamdani F. R1: if x is Л and (26) у is В then z is C

Sage n о F .R ¹:if x i s Л an d у is В the n f (х,у) is С

When and have crisp values fuzzification calculates the membership degrees for antecedent part.

Rule evaluation focuses on fuzzy operation (AA D / 0R ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Two most common methods that used in fuzzy logic controllers are Max-min aggregation and Sum-min aggregation. Max-min aggregation defined as below

Д и ⁽ Хк, Ук,Ю = д_{и;=1 FR}i (x_k, Ук, U)               (27)

= max {min '__t ^qO^yJ, Д_{Р т} ⁽Ю]}

The Sum-min aggregation defined as below

Д u (Х к , У k ,U ⁾ = Д^ _{F R} i (Х к , У к , Ю             (28)

= ^ m in '_ ! [д R _p q (Х k ,У k ), Д_{Р т}⁽Ю ]

where г is the number of fuzzy rules activated by x_k and y_k and also ^г р^к^Уи^-Л is a fuzzy interpretation of i — tA rule. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method (COG) and Centre of area method (COA) are two most common defuzzification methods, which COG method used the following equation to calculate the defuzzification

• •    Output defuzzification (fuzzy-to-binary [F/B] conversion).

III. METHODOLOGY

This step is focused on the design Madman’s fuzzy backstopping controller with application to continuum robot manipulator. As mentioned above pure backstopping controller has nonlinear dynamic parameters limitation in presence of uncertainty and external disturbances. In order to solve this challenge this work applied Madman’s fuzzy inference engine estimator in backstopping controller. The backstopping method is based on mathematical formulation which this method is introduced new variables into it in form depending on the dynamic equation of continuum robot arm. This method is used as feedback linearization in order to solve nonlinearities in the system. In this research fuzzy methodology is used to estimate the part of nonlinearity term in backstopping controller. The backstopping controller for continuum robot is calculated by;

U_B . _s = U_{eq B5} +M.I                            (31)

Where U_BS is backstopping output function, U_eqBS is backstopping nonlinear equivalent function which can be written as (23) and I is backstepping control law which calculated by (28)

U_e q Bs = [B + C + G]                           (32)

СОС(Х к ,У к )

^1и1^^^1.ди(Хк,Ук,и1)

^1^ ^^ .И и (Хк,Ук,и₁)

We have

I= [6i + K₁(K₁ — 1) • e + (K_t + K) • e"]        (33)

and COA method used the following equation to calculate the defuzzification

Based on (1) and (33) the fuzzy backstopping filter is considered as

СОА(Х к ,У к )

’Ll Ui-Hu(x_k,y_k, Uj) L^Дu■(.Хk,Уk, Ud

ZM ет ^(х) — As — к i=i

Where COG(x_k,y_k) and COA(x_k,y_k) illustrates the crisp value of defuzzification output, U , E U is discrete element of an output of the fuzzy set, д_и. (x_k,y_k, U) is the fuzzy set membership function, and r is the number of fuzzy rules.

Based on foundation of fuzzy logic methodology; fuzzy logic controller has played important rule to design nonlinear controller for nonlinear and uncertain systems [20-32]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of:

• •    Input fuzzification (binary-to-fuzzy[B/F]conversion)

• •    Fuzzy rule base (knowledge base)

• •    Inference engine

Based on (34) the formulation of fuzzy backstopping filter can be written as;

Where U eq B_5fu_ZZy = [(B +C+ G)] + T M=i в^т ^(x) + К

Most robust control designs are based on the assumption that even though the uncertainty vector ^ is unknown, some information is available on its bound.

In designing the robust backstopping controller, a robust term that compensates for the uncertainty in the system dynamics is added to the control law in (25) and (26). The robust control law, therefore, has the following form:

i_d = [я] + г

у = ^i + ([Я р ] + [Я^ + [Я р ] [Я й ]^ ! + W   ⁽³⁷⁾

The first three terms in (37) ensures the stabilization of the error dynamics in the absence of system uncertainties. The proper choice of w ensures the stability of the system even in the presence of uncertainties. Figure 1 shows a block diagram detailing the steps in the robust fuzzy backstopping control of continuum robot.

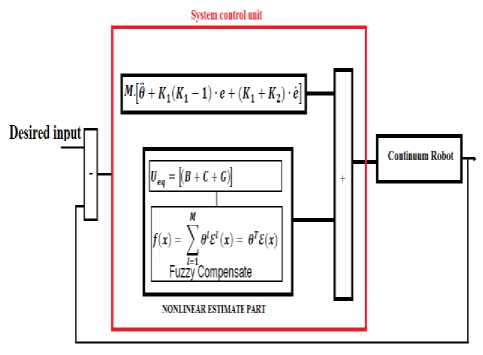
Figure 1: Block diagram of fuzzy backstopping for continuum robot

Using the control law in (35) and (37), the system error dynamics in (34) can be rewritten in the following form:

5 = [F]U[D](n-w)

where

[F] = ([П-РНЯ]) =

[][]

-[   ][   ]  -[   ] - []

К = [[Я р ][Я ^ ]   ^p ] + ^_dn ^r

When there are no uncertainties in the system dynamics, the robust term in the applied controller return is identically zero and the control law returns to the backstopping control developed in the previous section. The stability considerations and the design for the robust controller are determined using Lyapunov methods. The following positive definite quadratic function is selected as a Lyapunov function:

^ 1 = №>0  Vf*0

where [Q] E R ^6X6 is a positive definite matrix. The time derivative of the Lyapunov function along the trajectories of the error dynamics results in the following equation:

^ = f([F]r[Q] + [Q][F])f +

[ ][  ](  -)

Since, for a negative definite matrix [F]; a positive definite matrix [Q]; and a symmetric positive definite matrix [P], the following identity holds;

[F]r[Q] + [Q][F] = -[P]

the time derivative of the Lyapunov function in (49) can therefore be rewritten as vt = -fw + 2r [Q]DD](4 - w)

The time derivative of the Lyapunov function is strictly negative definite if the second term in the above equation is either negative or zero. The error dynamics converge to zero when the time derivative of the Lyapunov function in (42) is negative definite. Selecting the robust control term w as

-=«5Z      p>0

where z = [D]^r[Q]f substituting it into (40) results in the following expression for the time derivative of the Lyapunov function.

^-лго+^-йр)

According to the following inequality, zT(q-w) < ||z||||q||-p||z|| zr (ч-jpz) in (43) is always bounded from above by l|zH(HqH-P). Therefore, selecting p such that

P > HqH      Vxtxixid results in the negative definiteness of the time derivative of the Lyapunov function along the dynamics of f.

With the definition of q given in (31), the following bound can be put on the uncertainty term .

НчП = У/-[Я] - WKlIx _WH + Н[Я]НН^1 +      (47)

H[W]H) + H[W]- ¹ ИИчП < к Qm + КИЕ^ПКИ + кр + ^[Ям ^]Й

Using the inequalities in (43) and (44), p is solved to give the following relationship p > гЬ (кQm + кП№1ПHf И + [Ям]0 )           (48)

The choice of p from (48) ensures that the time derivative of the Lyapunov function is negative definite. This results in the stability of the error dynamics.

Vi = -fT[PR + 2zr(4-^z)<0         (49)

Vf *

• IV.    RESULTS AND DISCUSSION

Robust fuzzy backstopping controller (FBSC) was tested to Step response trajectory. In this simulation, to control position of continuum robot the first, second, and third joints are moved from home to final position without and with external disturbance. The simulation was   implemented in MATLAB/SIMULINK environment. These systems are tested by band limited white noise with a predefined 40% of relative to the input signal amplitude. This type of noise is used to external disturbance in continuous and hybrid systems and applied to nonlinear dynamic of these controllers.

Tracking performances: Figure 2 shows tracking performance for FBSC and BSC without disturbance.

Three joints

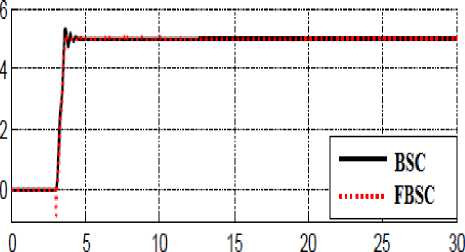
Figure 3: FBSC and BSC for first, second and third joint trajectory with disturbance.

Among above graph (3) relating to step trajectory following with external disturbance, BSC and FBSC have fairly fluctuations. By comparing some control parameters such as overshoot, rise time, steady state and RMS error it is computed that the FBSC's overshoot (1.6%) is lower than BSC's (3%). Both of them have about the same rise time; FBSC (0.5 sec) and BSC (0.49 sec) .

Three joints

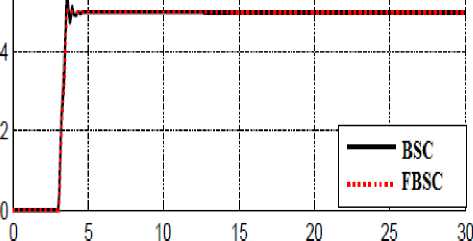
Figure 2: FBSC and BSC for first, second and third joint trajectory

By comparing step response trajectory without disturbance in BSC and FBSC, it is found that the FBSC's overshoot (1.4%) is lower than BSC's (1.6%) .

Disturbance rejection: Figure 3 has shown the power disturbance elimination in BSC and FBSC. The main target in this controller is disturbance rejection as well as the other responses. A band limited white noise with predefined of 40% the power of input signal is applied to BSC and FBSC. It found fairly fluctuations in trajectory responses. As mentioned earlier, BSC works very well when all parameters are known, or we have a limitation uncertainty in parameters.

• V.    CONCLUSION

Continuum robot is a nonlinear high degree serial robot. The dynamic parameters of this system are highly nonlinear. To control of this system robust backstopping methodology is introduced. Backstopping controller (BSC) is an influential robust nonlinear controller to certain and partly uncertain systems. When all dynamic and physical parameters are known BSC works superbly; practically a large amount of systems have uncertainties and fuzzy model base BSC is used. FBSC is a mathematical model base method to off-line control of highly nonlinear systems such as continuum robot.

ACKNOWLEDGMENT

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the Institute of Advanced Science and Technology (IRANSSP) Research and Development Corporation Program of Iran under grant no. 2013- Persian Gulf -2B.