Design Migration from Procedural to Object Oriented Paradigm by Clustering Data Call Graph

Published Online March 2016 in MECS

Software maintenance and change management are two of the “never ending” continuous processes in software development life cycle [1]. These processes involve the activities necessary to modify or improve an existing software product and requesting, planning, implementing and evaluating changes to the software system. The cost of such continuous processes largely depend on the design of the software system. Poor design may hinder the maintenance process by adding complexity and requiring additional effort and cost to mitigate those complexity.

The maintenance of legacy software [2, 3] often becomes costly and difficult due to its development paradigm. For an example, procedural programming was highly popular in earlier decades of software development and thus many legacy software were developed using procedural languages. The inherent limitations of procedural languages to deal with complexity and manageability of large code base make it troublesome to maintain such software [4, 5]. Moreover, it is difficult to ensure quality attributes like reusability [6], maintainability [7] and modularity [8] by using procedural paradigm.

Object oriented programming languages, by their design, provide better control on the code with proper use of its basic properties: Polymorphism, Inheritance and Encapsulation. For these reasons, migration to an object oriented languages is sometimes expected. A manual migration process can be very expensive in terms of cost of development, resource and time [9]. For large software system developed in procedural programming language, an automatic migration to object oriented design can effectively reduce this cost. This could be achieved by reverse engineering which helps to analyze a system’s internal elements and its external behavior and creating a structural view of the system.

One of the major challenge in any object oriented design is to ensure Encapsulation. It is defined as the bundling of data and functions that operates on the data together in a single component [10]. Encapsulation provides modularity in an object oriented design that helps in better manageability. Thus, a reverse engineering process of migrating procedural scheme to object oriented one must cover the encapsulation property of classes. To be more precise, it should properly define the class membership for each of the data and functions in the procedural code [11].

To solve the problem, we propose a heuristic approach to migrate from procedural to object oriented design. Our work has three major contributions: first, we represent a procedural program as a special type of graph, Weighted Data Call Graph, and apply Agglomerative hierarchical clustering on the graph. Second, we define a new similarity coefficient to measure similarity between nodes of the graph. Third, we score each level of the hierarchy by measuring cohesiveness [12], coupling [13] and modularity. The clustering level that produces highest score is considered to be the class design for the input procedural program.

Our work has extended the traditional call graph and defined the concept of the Data Call Graph (DCG). A call graph is defined as a human readable graphical representation of a program [14, 15, 16, 17]. In a call graph, each of the functions in the program are represented by a node. If a function calls another function, there is an directed edge from the first function to the later. In case of DCG, it includes data nodes along with function nodes of call graph. A weight is set on the edge of the DCG depending on the relationship represented by the edge and thus a Weighted DCG (WDCG) is produced.

A clustering scheme should be applied to WDCG to generate clusters which are candidate classes in the object oriented design [18]. We have applied Agglomerative hierarchical clustering [19, 20] on WDCG to find the class design from procedural program. Agglomerative clustering requires calculation of similarity between nodes of the graph. There is a number of similarity measures to calculate similarity between nodes of a graph. However, none of them are applicable to weighted graphs. Therefore, we have defined a Weighted Distance Matrix (WDM) to measure similarity among nodes in a weighted graph.

In the migration process we create a hierarchy of clusters on the WDCG using Agglomerative clustering. Then we search a level in the hierarchy that gives maximum output to an objective function based on three attributes of an object oriented design: coupling, cohesion and modularity. That is, we followed the principle that a design should be as modular as possible, the members of a class should be highly co-related and any pair of classes should be as decoupled as possible. These quality attributes are widely accepted in the existing literature [18, 21, 22, 23]. The clusters generated in this way give clues to classes in the object oriented design.

We have performed an empirical evaluation of the design migration process by calculating similarity between output produced by our technique and manual object oriented de- sign. The manual designs are prepared and evaluated by a group of professional software engineers from three Software Development Companies (Jantrik Technologies Ltd. , Genweb2 , Therap (BD) Ltd. . Five C programs of variable size have been used in our evaluation and the similarity was measured using Jaccard similarity coefficient. It has been seen that in best case, the approach yielded 100% similarity and in average case the similarity turned out to be around 75.6%.

Rest of the paper is organized as follows: Section II dis- cusses the state of the art on design migration. The new terms that have been introduced in this work is presented in Section.

• III.    Section IV discusses the design migration methodology by clustering Weighted Data Call Graph. Verification and validation of the proposal is presented in Section V. Finally, the concluding remarks along with future research direction is provided in Section VI.

• II.    Related Works

Since the evaluation of object oriented concept, migration from procedural to object oriented paradigm has been ad- dressed as a major research problem. However, most of these works focus on code-level migration, rather than addressing the migration in design level. By code-level migration, we mean that a program is simply translated from one language to another, whereas we focus on migrating the design from one paradigm to another. This section highlights some of those major contributions in design migration.

Sneed et al. [24] introduced the concept of code to design migration. The work converts a COBOL program to an object oriented design document by capturing and documenting the sequence of operations executed in a COBOL system. The work identified different types of objects like user interface objects, information objects, file objects, view objects, etc. This work is only for COBOL and does not generalize for all procedural languages. They also developed a tool ‘ObjectRedoc’ using C and MS-Access running under MS-Windows and used it to help downsizing of mainframe legacy systems.

There has been work where researchers aim to decompose a software system to subsystems to understand its behavior [25]. Their work is based on software clustering technique that uses both static and dynamic information from the source code. Nevertheless, their work does not provide any guideline to produce classes for object oriented design. Works of similar nature, in the context of software architecture recovery and modularization, have been reviewed by Maqbool et al. [26]. Their work analyzed the clustering process of multiple clustering algorithms using multiple criteria and showed how arbitrary decisions taken by these algorithms effect the quality of the clusters.

Heroux et al. [27] presented the architectural comparison of commercial software and scientific research software. They found that commercial software are written for the purpose of generating revenue where the underlying algorithms and methodologies are mature. On the other hand the scientific research software in computational science and engineering disciplines are developed for new algorithms and computational capabilities which are less modular and largely unaware of standard industry concepts and practices.

The work in [9] used relational database for transforming object oriented design from procedural system. The migration was done in two phases. Firstly, object identification form procedural program and secondly, translation of the old one into new object oriented system. They implement three algorithms presented in [28, 29] for identifying objects in procedural software namely global based object identifier (gboi), type based object identifier (tboi), receiver based object identifier (rboi). These methods were applied to a 3000 line program written in C, and rboi performed better in identifying classes. Khan et al. [30] compared procedural programming with object oriented programming and proposed a migration approach from procedural to object oriented language. This approach bind object on the basis of hierarchical dependency of classes instead of clustering function together. This study focused on the structural difference between the procedural and object oriented programs and concluded that object oriented programming increases software reliability and modifiability by decoupling specification and implementation, and allows software code to be extensible, reusable and maintainable.

The method of finding object-like feature in code presented in [29] is based on global data or data type. They define class as a set of data, type and function. First method considers only the global variable and represent a program as a graph based on the use of variable in a routine. If a variable is used by a function, then they are connected by an edge. Each of the connected components in the generated graph are considered individual classes. This highly optimistic method is very likely to generate large classes with many responsibilities.

Van Deursen et al. [20] presented clustering with concept analysis for identifying objects in legacy code. This object identification approach uses clustering and concept analysis separately and result is merged together to overcome the shortfall of clustering technique. The method uses concept analysis to determine number of classes and uses Agglomerative clustering to identify classes. The proposed identification technique was applied to a real life legacy COBOL system to evaluate performance. However, their work focuses on code translation, rather than addressing the migration in design level.

A framework for migrating procedural code to object oriented platforms is presented in [21]. This framework generates Abstract Syntax Tree and then this tree is translated in to extensible markup language (XML). This XML is analyzed for identifying class based on the global data and variables. The work focus on minimizing coupling and maximizing cohesion. The method was applied at the IBM Center for Advanced Studies of IBM Toronto Lab for C to C++ migration. This framework can also be used to identify reusable components. The work in [31] recognized the maintenance and evolution of large software as difficult. To make such software understandable, they used directed graphs to represent software modules and their dependencies. This representation, although hides a lot of details, might be complex and therefore, partitioning closely related modules into clusters was considered as a suitable approach to comprehend the complex design. They presented a genetic algorithm based clustering technique to identify the modularity of a procedural system. They success- fully applied this approach in Mini-Tunis [32] software and validated by comparing with the original documented design. In 2011 Dineshkumar et al. [19] presented an empirical approach to migrate from structured program to object oriented design. They introduced a new technique for code to design migration, which creates Agglomerative cluster using Jaccard distance matrices. They initialized the relationship between variables and functions of the structured program using Jaccard distance measure that leads to grouping or clustering. They represented the result in UML and conducted a comprehensive industrial survey to evaluate the accuracy of their proposal. Their use of Jaccard distance as a measure of distance between clusters considers all types of relationships to be equally contributing to the distance between the clusters. In 2013 Siddik et al. [18] modeled structured to object oriented design migration as a optimal graph clustering problem. However, this model was realized to be computationally hard. The work presents eight heuristic algorithms based on Monte Carlo and Greedy approaches and formulated the κ-index for measuring the quality of a cluster. Clustering coefficient (Ψ) and characteristic path length (χ) were also used for assessing the quality. This approach only considers functions to be potential member of class ignoring variables and constants. They used high coupling, low cohesion and large number of objects as the objective.

The work of Siddik et al. [18] was extended by Selim et al. [33] and Siddik et al. [34]. Selim et al. [33] presented a genetic algorithm for finding optimal clustering of call graph with an objective to maximize the number of intra-cluster edge and minimize inter-cluster edge. This work outperforms the previous work [18] of Greedy and Monte Carlo by 40% and by 49.5% respectively. Siddik et al. [34] also extended their previous work [18] and proposed two variations of local search heuristic. Selim et al. proposed an extension over this work based on variable neighborhood search [35]. However, these works ignore variables and constants of the procedural code as decision parameters for determining class.

The review shows that only a few of the works directly proposed a method that focus on migrating procedural design to detailed object oriented design. Those approaches do not yet solve design migration problem. To overcome the limitations in the existing literature, we propose a new heuristic approach to migrate a procedural design to an object oriented design, which considers functions, global data and parameters of the procedural code as a basis for the intended reverse engineering.

• III.    Proposed Terminologies

In this section we propose the terminologies, notations and equations to support the design migration technique. We propose a new type of graph, Weighted Data Call Graph (WDCG), to represent a procedural program. To compute similarity between two nodes of WDCG, we introduce a new similarity measure called Weighted Distance Matrix (WDM). Moreover, we propose a data structure, Entity Map that incorporates certain weights along with Entity Set [19] to calculate the value of WDM.

These concepts are elaborated in the following subsections.

• A.    Weighted Data Call Graph

Call graph is a widely used representation for program analysis. A number of related works have used this representation for their design migration techniques [18], [34]. Although very useful, call graph limits the program representation only to functions or classes; however, the variables and the constants of a program are also important members of the design. We extend call graph to Data Call Graph (DCG) where variables and constants are also represented by nodes. We do not identify variable and constant separately and use the term data to mean any of them. In a DCG there are two types of nodes:

Function Node : Node to represent functions. We ignore the system functions and external library functions because they are out of the scope of design migration. Only the functions defined in the program to migrate are considered.

Data Node : Node to represent data. Like the Function Node, we exclude the system data and external library data and include only the data declared within the program to migrate. Data nodes include constants, variables, pointers and dynamically created variables.

There are four types of edges in DCG:

Self-Edge : Every element is connected to itself by a self-edge. Because self-edge exists for all elements, we do not show those in DCG.

Call Edge : When a function calls another function, there is a call edge from the first function to the second. Call edge is identical to the edges in call graph.

Read Edge : There is a read edge from function f to data d if and only if d is read in f. Reading may occur by reading a global variable or reading a variable passed as argument to the function.

Write Edge : There is a write edge from function f to data d if and only if d is written in f. Writing may occur by writing a global variable or writing a variable passed by a pointer or reference to the function.

All types of relationships between a pair of elements cannot be considered equal, therefore we put weight on the edges of DCG depending on the relationship of represented by the edge. We call the resultant graph a Weighted Data Call Graph (WDCG). The weights are not absolute but relative. That means, the value of the weight of different type of edges are not important, but the ratio among them are important. We have considered weight of self-edge to always be $1$ and assigned weight to call edge, read edge and write edge from a predefined set of weights.

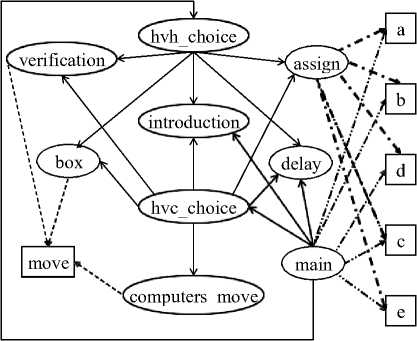
This example has been used throughout this paper to illustrate different aspects of our work. The program has 9 functions and 6 global variables. Therefore the DCG has 9 function nodes and 6 data nodes. Different edges representing function calls and read/write operations are also shown in Figure 1.

Call Edge

Write Edge

Read Edge ■

Read and Write Edge

Node

FunctionNode

Fig.1. Data Call Graph of the Pebble Dropping Program Showing All Types of Nodes and Edges

• B.    Entity Map

The notion of Entity Map is similar to entity set [19] which is used to calculate similarity between two programming elements. The similarity is used in Agglomerative clustering technique. However, we cannot use entity set directly because it works only with unweighted relationship between programming elements. Therefore, we extend entity set and define entity map. Before discussing entity map, we formally define entity set as follows:

The entity set of a function f, (E f ) is defined as,

Ef= {g∶ g is a function called by f} ∪{ԁ∶ d is a data used by f}∪{f}

• i .e., entity set of a function includes the functions it calls, data accessed by the function and the function itself.

The entity set of data d, (E d ) is defined as,

Ей = {g∶ g is a function that use d} ∪{f} i.e., entity set of a data includes the functions that access that data and the data itself.

Therefore for the DCG in Figure 1

^mam ⁼{ main , delay , introduction ,ℎ vc _ c ℎ oice , ℎ v ℎ_ℎ oice , a , b , c , d , e } —                *    *    *    *    *     1

^move ⁼{ move , verification , box , computers _ move }

While elements of entity set are programming elements (function or data), elements of entity map are ordered pairs where first entry is a programming element and the second entry is a number representing weight of the relationship.

Entity map of an element contains the element itself paired with self-weight ( ws ). In addition, entity map of a function contains the set of pair of the function it calls and call weight ( wc ), the set of pair of the data it writes and write weight ( ww ), and the set of pair variables it reads and read weight ( wr ). Entity map of a data contains the set of pair of the function which writes the variable and ww , and the set of pair of function which reads the variable and wr . Formally entity map of function f,

ef = {(f, ws)} u {(5, wc): g is a functi о n с a 11ed by f } и {(dw, ww): dw is a data woitton bу f }

u {(dr, wr): dT is a data read Уу f } гй = {( d, ws)}

u {(Ww, ww): Ww is a fuction t^at woi tas d}

u {(Wr, wr): gr is a func ti 0 n t^ at oaads d}

Therefore in the DCG in Figure 1

e_m a tn = {(m a in, w_s), ( d e Iyy , w_c), (in tooduc ti 0 n , w_c), ⁽huv_chotce, w_c), ⁽huv_ch01_ce, w_c),

(a, wr),(b, wr),(c, wr),(d, wr),(a, wr)} em о ve = {(m o oe, ws), (vao ificati 0 n wr), (b 0 x, wr), ( c o mp и t ors_m 0 oe, wr)}

Entity map of a programming element is actually a binary relation, where domain is the programming elements and co-domain is real number. The elements of entity map are called weighted entry . For entity map, we define the following terms:

Merged Entity Map : In an entity map weighted entries ( a, w)), (a,w₂), ..., (a, w_x) can be replaced by the single weighted entry (a, £1 w_t). This operation is called merge and if we merge all possible merge-able weighted entries in Q and the result is entity map L, we call L is merge of Q. Merge of Q is denoted by M(Q).

Element Set : Element Set of an entity map is the set of the programming elements in the entity map. Element Set of an entity map Q is denoted by E(Q).

Weight Sum : Weight Sum of a entity map is the sum of weights of the entity map. Weight sum of an entity map Q is denoted by S(Q).

Weighted Intersection (A_w) : Weighted Intersection is an operation of two or more entity maps where the result of the operation is an entity map R for which (a, w) E R if and only if a E 7 and (a, w) E U where I is the intersection of element set of the operands and U is union of all operands. Weighted intersection of two entity maps Q ! and Q ₂ is denoted by Q _г A_w Q ₂.

Weighted Union (uw): Weighted Union is an operation of two or more entity maps where the result of the operation is an entity map for which ( , ) E if and only if ( , ) E where   is union of all operands.

Weighted union of two entity maps and is denoted by u     .

• C.    Weighted Distance Matrix

Before defining the concept of Weighted Distance Matrix (WDM), we need to define Weighted Similarity Coefficient (WSC). WSC is a variant of Jaccard Similarity Coefficient which is a widely used similarity measure in hierarchical graph cluster analysis. We cannot directly use this coefficient because of the weights on the edges of WDCG. Therefore, we define WSC whose semantics is similar to that of Jaccard’s coefficient.

Jaccard Similarity between two finite sets A and B is defined as:

|ЛПВ| J (л ,s ) = ЙЦ^

We define Weighted Similarity Coefficient (WSC) between two entity maps A and B as follows:

(A ) /G4^^)

Jw( , ) S(4uwS)

WSC hold the following properties:

Range : The value of J _w (4, В ) is between 0 and 1. Inclusive the value is 0 when 4 A_w В is empty and the value is 1 when 4 A_w В = 4 u_w В . For all other cases, the value is in between 0 and 1.

Symmetry : WSC is symmetric, i.e., for any two entity map A and B,

Jw (4 ,B )=Jw(B ,4 )

We can use the notion of WSC to calculate the weighted distance between two entity maps A and B. It can be formally defined as,

Dw (4,B) = 1 - 5(ЛПи,В)              (1)

^wV ,             5(Л u_wB)                 ⁽ )

Weighted distance holds the properties of WSC. The conditions range property is reversed, i.e.,  1 when

4 Aw B is empty and 0 when 4 Aw B =4 uw B.

A Weighted Distance Matrix (WDM) X can be calculated for a set of entity maps M_x , M₂ ,.., M_n, where for each entry X(i, j) represents the weighted distance between M and M . Formally,

X (i, j) =Dw(Mt,Mj),    V i,j

WDM holds the following properties:

Squareness : Each column and each row of a WDM represent one and only one entity map. Therefore number of rows and number of columns are equal to number of entity maps.

Symmetry: In a WDM M, M(i,j) = Dw(Mt,My) and M(j, i) = Dw(M;-,Mt). According to Symmetric property of weighted distance, right side of the two equalities are equal. Therefore M(i, j)= M(j, i) which means M is symmetric.

Hollow Matrix : M(i , i) represents the distance from an element to itself which is zero. Therefore, M(i , i) is 0 for all distance matrix M making it a Hollow matrix [36].

• IV.    Design Migration

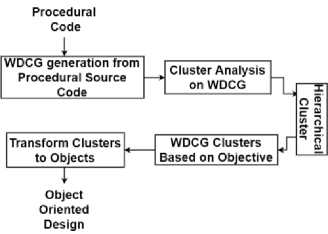
In this section we present the proposed design migration method. The migration process is done in three main steps. In the first step we generate a WDCG from a procedural program. The next builds a hierarchical cluster tree of the WDCG using Agglomerative clustering technique. In the last step, we define an objective function and find a level in the hierarchy that maximizes the objective function. This optimal clustering is the object oriented design where each cluster of this clustering is a candidate class. The steps are illustrated in Figure 2 and are elaborated in the subsequent sections.

• A.    Weighted Data Call Graph Generation

This step takes a procedural program and produces a Weighted Data Call Graph for the program.

We have discussed about the elements of WDCG in Section III.A. Common graph representations like adjacency matrix, adjacency list, incidence matrix and incidence list do not support different type of nodes. Therefore, we have defined a technique to represent WDCG. The technique is a context free grammar [37] with the following rules:

Keyword: There are five keywords: ?function, ?data, calls, reads and writes . The first two keywords are declaration keywords and others are relation keywords.

Identifier:  Identifiers can be words except the keywords and may contain any characters except whitespace characters. Also, identifiers cannot start with a question mark (?).

Statement:  The statements are separated with semicolon (;). There are two types of statement:

• •    Declaration Statement: Declaration statements are used to state which elements are present in the WDCG. One statement declares exactly one element. Declaration Statement starts with one of the declaration keywords and then an identifier. If the declaration keyword is? unction , then the identifier is name of a function and if it is ? data the identifier is name of a data.

• •    Relation Statement: A relational statement indicates relationship between two elements. Relation statement starts with an identifier then a relation keyword then another identifier. The identifier are names of elements declared before the current statement. A calls relation statement has two function elements linked with a calls keyword that indicated the left function calls the right function. A reads/writes relation statement starts with a function element and then the keyword

reads/writes and then a data element. This statement indicates that the function reads or writes the data.

The WDCG notation of the Pebble Dropping Program is illustrated in Listing 1. In the listing, initially all the functions of the code are declared. The next section includes all the data declarations. Finally the relation statements are provided.

f ig .2. o verall p rocess for p roposed d esign m igration .

Listing 1. WDCG notation for Pebble Dropping program

? function main;

? function assign;

? function hvc_choice;

? function hvh_choice;

? function verification;

? function introduction;

? function box;

? function computers_move;

? function delay;

? data a;

? data b;

? data c;

? data d;

? data e;

? data move;

main writes a;

main writes b;

main writes c;

main writes d;

main writes e;

main writes e;

main calls hvc_choice;

main calls hvh_choice;

main calls delay;

main calls introduction;

assign writes a;

assign writes b;

assign writes c;

assign writes d;

assign writes e;

assign reads a;

assign reads b;

assign reads c;

assign reads d;

assign reads e;

hvc_choice calls assign;

hvc_choice calls verification;

hvc_choice calls delay;

hvc_choice calls introduction;

hvc_choice calls computers_move;

hvc_choice calls box;

hvh_choice calls assign;

hvh_choice calls verification;

hvh_choice calls delay;

hvh_choice calls introduction;

hvh_choice calls box;

verification reads move;

box reads move;

computers_move reads move;

• B.    Cluster Analysis

Although significant works have been done on non-hierarchical clustering techniques [38,   39,   40], hierarchical techniques [41, 42] are more appropriate in our case as it gives the opportunity to choose the clustering that gives the best result of a predefined function. Moreover, non-hierarchical techniques usually

Algorithm 1 Build Cluster Hierarchy

Input: Г the set of programming elements

• 1:    function BuildClusterHierarchy (Г)

• 2:      currentClusters ← Г

• 3:      hierarchy ← { currentClusters }

• 4:      while size of currentClusters > 1 do

• 5:       ( Ci , Cj )←

ClosestClusterPair ( ClosestClusters )

• 6:       currentclusters ←

( currentclusters { c₍ , ^CJ }) ∪ {{ Cj , Cj }}

• 7:      ℎ ierarc ℎ •y ←

ℎ ierarc ℎ у ∪   { currentclusters }

• 8:      end while

• 9:      return ℎ ierarc ℎ у

• 10:    end function

• 11:   function ClosestClusterPair ( clusters )

• 12:   minD ←∞

• 13:    minCj ← NULL

• 14:    minCj ← NULL

• 15:     For each с, in clusters do

• 16:       For each Cj in clusters do

• 17:       d ← D_w ( ^ct , Cj )        ► See Equation 1

• 18:        If cl <  minD then

• 19:       minD←

• 20:        minCj←

_

• 21:        minCj←

• 22:       end if

• 23:      End for

• 24:    End for

• 25:    mainPair ←{ mine, , minCj }

• 26:    Return mainPair

• 27:   End function

require information like number of clusters, cluster size, etc. [43] which are not available in our context. We have implemented a classical Agglomerative hierarchical clustering [19, 20] technique for generating clusters from WDCG. For the distance measure, we have used weighted distance measure described in Section III.C.

In our implementation we find one level of hierarchy at a time, starting from each nodes in different clusters to all nodes in one cluster. If we have n nodes, there will be $n$ hierarchies. In each iteration, we find the closest pair of clusters, then create the new level by removing the pair from current level and adding the pair after merging. The iteration stops when the current level has only one cluster, i.e., all nodes are in one single cluster. These steps are presented in Algorithm 1.

The function BuildClusterHierarc ℎ У will return a hierarchy of clusters given a set of programming elements. The function ClosestClusterPair finds the closest pair in a set of clusters. The closeness is measured by weighted distance function defined in Equation 1. BuildClusterHierarc ℎ У function has one loop that runs n=|Г| times and invokes ClosestClusterPair with currentclusters inside the loop. Function ClosestCluster Pair has a two level nested loop, each of the loops runs m=| currentclusters | times. Therefore the worst case run-time complexity is 0 ( mn² ).

Figure 3 shows the Agglomerative clustering steps with a set of predefined weights over the Pebble Dropping program. We assume that self-weight is 1, call weight is 0.1, read weight is 0.2 and write weight is 0.4. The numbers in the small circular nodes indicate the step number, that is, in which step two clusters were merged. These node also indicate a cluster composed of two other clusters from each of which there is an edge to this node. In the very beginning verification and move are the closest pairs and they merge into 1. In the next step main and assign are closest, therefore they merge into 2. The process continues until all clusters merge into 14.

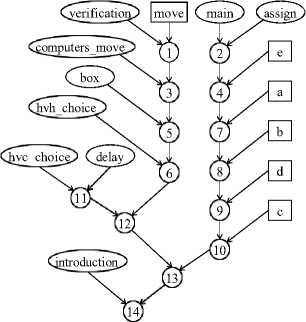
Fig.3. Step by Step Clustering.

• C.    Identifying the Desired Clusters

Each of the levels in a cluster hierarchy are candidates for being the object oriented design. We measure the quality of a level by three quality attributes of a class: high cohesion, low coupling and high granularity [18, 23]. For this purpose we define an objective function that is evaluated against each of the levels. The level that optimizes the objective function is selected as the object oriented design.

Siddik et al. mathematically formulated the problem in [18] as follows:

Let G(V,E) be the underlying undirected graph of a call graph. The nodes in same cluster are labeled with same number and nodes in different clusters are labeled differently. V and E be the set of vertices and edges respectively. We define variables l, x, y and z as follows:

с = { 1 if vertex v is head of a cluster

= {

X = { 1 if edge e connects nodes with same label

= {

• Y. = { 1 if edge e connects nodes with different label ^{= {}

z   ={1 if vertex v has label c

, ={

The work in [18] formulated the problem as:

Maximize ∑ X_e -∑

ye

+∑| C„ |, ∀ e ∈ E , ∀ v ∈ V

V

Subject to:

X_e + Уе =1,     ∀ e ∈ E

Lg

∑ Z. , =1,    ∀ V ∈ V

C=1 l_g

∑ z_a , . Z_b , =  , „ , ∀ a , b ∈ E

= ⋃   , ∀ =1,2,…,

к

Here Су indicates if vertex v is head of a cluster, therefore ∑ V Су is the number of clusters. The objective function presented in Equation (2) maximizes intracluster edges, minimizes inter-cluster edge and maximizes number of clusters. The objective function is not normalized. We can perform comparison between clustering on same graph, however, we cannot compare between clusters of different graphs. That means, given a graph, we can determine the best clustering, but cannot state how good this particular clustering is. Because of these limitations, we use a modified version of this objective function.

We call our objective function the Omega function or simply Omega (Ω). Let G(V, E) is the underlying undirected graph of a clustered WDCG. The nodes in same cluster are labeled with same number and nodes in different clusters are labeled with different numbers. The labels start from 1 and ends to number of clusters. We define the following variables for this graph:

w_e = weight of an edge e

Lg = number of labels in graph G

= { w_e if edge e connects nodes with same label

= {

= { w_e if edge e connects nodes with different label

= {

7   ={1 if vertex v has label c

, ={

The variables Lq , x_e and Уе are normalized as following variables for graph G ( V , E ):

к =_| V _|

5_g = ^∑ eXe , ∀ e e E SG

∑ еУе

9g _{=   ,∀} e e E

SG

Where G is defined as,

^G =  , ∀ e e E

We call variables Pg , 5 g and 9 g cluster density, intracluster edge density and inter-cluster edge density respectively. Pg indicates number of clusters per vertex. 6 g Indicates ratio of intra-cluster edge with respect to total number of edges and 9 g indicates ratio of intercluster edge with respect to total number of edges. Cluster density corresponds to modularity, intra-cluster edge density corresponds to cohesion and inter-cluster edge density corresponds to coupling of clusters respectively. As these clusters represent the classes in the object oriented design, we want that the design should be as modular as possible, highly cohesive and loosely coupled. Based on these we define our objective function Ω:

Maximize Ω( G )= 5g - 6_G + Pg (3)

Maximizing the values of 6 g and Pg and minimizing value of 9 g will maximize Ω. However, maximizing Pg minimizes 6 g and maximizes 9 g . When each vertices are in different clusters, Pg has its maximum value, which is 1. In this case all the edges are inter-cluster which results 6 g to be 0 and 9 g to be 1. Pg is minimum when all clusters are in same cluster. In this case 6 g has its maximum value 1 and 9 g has minimum value 0. Mathematically:

0< Pg ≤1 0≤ 5g ≤1 0≤ 6g ≤1

When applying Agglomerative clustering on the WDCG, clustering of each step is a candidate object oriented design. We apply the objective function Ω on clustering of each of the steps. The step that produces the maximum value of Ω is considered to be the optimized clustering.

• D.    Properties of Obtained Classes

Each of the clusters in the optimized clustering corresponds to a class in the object oriented design. In addition to the function and data membership, we can derive has-a relationships among the classes. When a cluster has a inter-cluster edge to another cluster, the class corresponding to the second cluster belongs to the class corresponding to the second cluster, i.e., the first class has the second class. Moreover, we can also identify access levels of the members of a class. If there is one or more inter-cluster edge incident to a member of a class, the member is public. It is private otherwise.

For the Pebble Dropping program, step 10 from the Figure 3 produces the maximum value of Ω. Figure 4 shows the class diagram for clusters this step. There has a relationship within the classes and the access level are also shown in the class diagram. The class design proposed by a group of professional software engineers is shown in Figure 5. We call this design the expected class design. It is seen that though the number of classes in the diagrams are not equal, the larger classes are nearly identical.

• V.    Evaluation

We have implemented the proposed procedural to object oriented design migration technique and performed an empirical evaluation. In this section we present the evaluation process and analyze the result.

• A.    Experimental Setup

We have analyzed the result with five C programs. Some of the data for the evaluation process are collected from academic projects of Institute of Information

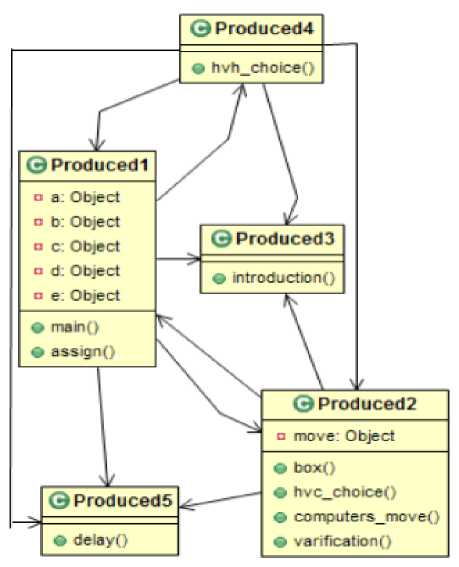
Fig.4. Produced Class Design of Pebble Dropping Program

Technology, University of Dhaka and the others are collected from online repositories. The data set are of different size having varying number of programming elements. Size of the individual data set are given in Table 1. The scheme was implemented in Java platform and the source code is hosted on Bitbucket ( bitbucket. отд / mo ℎayemin/designmigration ) project hosting service.

Four engineers helped us in the evaluation process. Among them two are software engineers having three years of experience. They prepared an object oriented design for each of the dataset. Their designs were reviewed by two other engineers. One of them is a Principal Software Engineer specialized in object oriented design. The other is a Project Manager specialized in design patterns. Both of them have more than eight years of industry experience. In addition to experience in software industry, they are also guest lecturers in their specialized fields at Institute of Information Technology, University of Dhaka. We have considered the designs provided by this group of people as benchmark for result evaluation.

• B.    Evaluation

For each dataset, we have calculated similarity between design produced by our technique with result provided by a group of software engineers using Jaccard similarity coefficient. For calculating similarity of a dataset, we take classes generated by our technique. We call this class design actual class design and the class design provided by the group of software engineers expected class design. For each of the actual classes, we find a best matching cluster in the expected classes. If no matching pair is found for a class, it is paired with class with no members.

0 Expected 1

• □    a: Object

о b: Object a c: Object о d: Object

• □    e: Object

G main():void в assign():void 0 hvc_choice():void 0 hvh_choice():void 0 introduction():void 0 delay():void

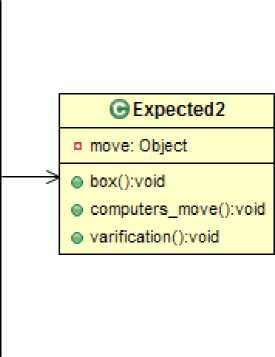
Fig.5. Expected Class Design of Pebble Dropping Program

Let, E = {{a, b}, {c, d, e}, {f, g}, {h, i, j, k}} be the expected clustering of an procedural code and A = {{a, b}, {c, d}, {e}, {f, g, h}, {i, j, k}} be clustering generated by our system. Here each c ∈ E ∪ A are clusters and each e ∈ C are members of cluster. For example, h, i, j and k forms a cluster in expected result. We use p, Pe and Pa. to denote a pair, expected set of the pair and actual set of the pair by respectively. We establish the following mapping for E and A:

pair ( p )	pair ( p )	pair ( p )
1	{ a , b }	→	{ a , b }
2	{ c , d }	→	{ c , d , e }
3	{e}	→	{}
4	{ f , 9 ,ℎ}	→	{ f , 9 }
5	{ i , j , к }	→	{ℎ, i, j , к }

We measure distance between a pair with the Jaccard Similarity Coefficient. For a pair p similarity

^| Pa ∩ Ре ^|

^∅ P =_| Pa ∪ Pe |

\ ю I — i ^, i ^, к }∩{ h. ^, i ^, к ^, i }

For example, similarity of pair-5 is              =

• p,             y p            _{ i , j , к } ∪ { h. , i , к , I }

0.75 . We calculate the similarity between each pair. Direct mean of the pairwise similarity will produce incorrect result. Because we expect that a large expected cluster should have more effect on the final similarity than a small expected cluster. To achieve this, we calculate weighted sum of the pairwise similarities. Weight of a pair is ratio of the cardinality of expected clustering to the total number of elements in all clusters. For a pair p, we define

Weighted Pair Similarity, Фр=| - |.∅ P     (4)

| E |

Finally, similarity of all pairs P of a data set D :

Фп =∑ p фр , ∀ p ∈ p            (5)

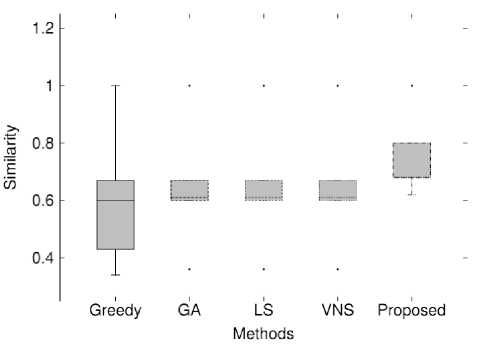
Fig.6. Box Whisker Plot Representing the Similarity between Expected and Actual Class Design for Different Programs using Different Methods.

We run the same process with a single data by changing weights of different type of edges in WDCG. We set value of self-weight to 1. For other three weights, we use values from 0.1 to 0.6 with an interval of 0.1. We find the weight that generates best result for each data and these results are shown in Table 1. We can see that for the best case call weight, read weight and write weights are 0.1, 0.4 and 0.5 respectively.

The proposed approach was compared with recent state of the art techniques. The result is shown in Table 2. It can be seen that the proposed method have outperformed the state of the art techniques. To better visualize the performance, the similarity using each approaches for each of the five programs is presented in Figure 6. From the figure it can be seen that the score of proposed scheme is not only higher but also more consistent than other techniques.

Our experiment found that Ω is biased towards value of β, i.e. the measure of modularity. Generated results created more clusters than the ones suggested by the software engineers. For many cases we found pair p where Pe ={} which results Фр to be 0. Expected clustering for first three programs were all the elements in a single class. These three programs were very cohesive therefore produces high X in Ω. For first two data the cohesiveness were strong enough to overcome bias of modularization thus produced desirable results.

From Equation 4 we can derive, for a pair P , Фр ∝ | Pe . In most of the cases, the value of Pa turns out to be small when the value of Pe is 0. This is because large classes are more likely to find a matching class than small classes. Therefore larger ∅ values are multiplied with larger | Pe | values and small ∅ values are multiplied with zero or small values. This helps to prevent excessive number of small classes in our design that introduces high coupling. In other words, it allows to keep balance between modularity and coupling making the overall similarity satisfactory.

• VI.    Conclution and Future Work

This paper introduces a new technique for migrating the design of procedural program to object oriented architecture. We have formulated this design migration scenario as a weighted graph clustering problem. We have introduced new concepts in the literature to support our technique: Weighted Data Call Graph, a grammar to represent Weighted Data Call Graph, and a special type of set called entity map and operations specific to entity map. An inverse variant of Jaccard Similarity Coefficient called Weighted Distance Matrix has been proposed to compute similarity between two nodes of a weighted graph. Similar nodes based on high modularity, high cohesion and low coupling are clustered using Agglomerative Hierarchical Clustering. Each of the clusters are then considered as a class.

We have applied our technique on five C programs. The results produced by our technique have been compared with designs provided by a group of professional software engineers. Similarity between engineers' design and the design generated by our system has been calculated using Jaccard Similarity Coefficient. The experiment shows that in best cases the approach yields identical designs and on average case the designs are 75.6% similar. The proposed system can identify optimal clusters as potential classes of a system. Our future plan is to identify interfaces that classes implement.

Table 1. Results of Experiments Illustrating the Performance of the Proposed Scheme

Application Name	Call Edge Weight	Read Edge Weight	Write Edge Weight	similarity Ψ
LCS	0 . 40	0 . 20	0 . 40	0 . 83
Supermarket				0 . 68
Student Report Card				0 . 68
Pebble Dropping				0 . 28
Calendar				0 . 33
Average				0 . 56
LCS	0 . 20	0 . 20	0 . 60	0 . 83
Supermarket				0 . 68
Student Report Card				0 . 68
Pebble Dropping				0 . 80
Calendar				0 . 33
Average				0 . 664
LCS	0 . 20	0 . 30	0 . 50	0 . 83
Supermarket				0 . 68
Student Report Card				0 . 68
Pebble Dropping				0 . 80
Calendar				0 . 33
Average				0 . 664
LCS		0 . 30	0 . 60	1 . 00
Supermarket	0 . 10			0 . 68
Student Report Card				0 . 68
Pebble Dropping				0 . 80
Calendar				0 . 33
Average				0 . 698
LCS	0 . 10	0 . 40	0 . 50	1 . 00
Supermarket				0 . 68
Student Report Card				0 . 68
Pebble Dropping				0 . 80
Calendar				0 . 62
Average				0 . 756

Table 2. Results of Experiments Illustrating The Performance of The Proposed Scheme in Terms of Ψ

Application Name	Greedy [18]	GA [33]	LS [34]	VNS [35]	Proposed
LCS	1.00	1.00	1.00	1.00	1.00
Supermarket	0.67	0.67	0.67	0.67	0.68
Student Report Card	0.43	0.36	0.36	0.36	0.68
Pebble Dropping	0.34	0.61	0.61	0.61	0.80
Calendar	0.60	0.60	0.60	0.60	0.62
Average	0.608	0.648	0.648	0.648	0.756

Moreover, considering each identified classes as clusters, we can apply a second layer of Agglomerative clustering and mark the result as components.

Acknowledgment