Design New Intelligent PID like Fuzzy Backstepping Controller

Published Online February 2014 in MECS DOI: 10.5815/ijmecs.2014.02.03

Continuum robots represent a class of robots that have a biologically inspired form characterized by flexible backbones and high degrees-of-freedom structures [1-3]. Theoretically, the compliant nature of a continuum robot provides infinite degrees of freedom to these devices. However, there is a limitation set by the practical inability to incorporate infinite actuators in the device. Most of these robots are consequently under actuated (in terms of numbers of independent actuators) with respect to their anticipated tasks. In other words they must achieve a wide range of configurations with relatively few control inputs. This is partly due to the desire to keep the body structures (which, unlike in conventional rigid- link manipulators or fingers, are required to directly contact the environment) “clean and soft”, but also to exploit the extra control authority available due to the continuum contact conditions with a minimum number of actuators. For example, the Octarm VI continuum manipulator, discussed frequently in this paper, has nine independent actuated degrees-of-freedom with only three sections. Continuum manipulators differ fundamentally from rigid-link and hyper-redundant robots by having an unconventional structure that lacks links and joints. Hence, standard techniques like the Denavit-Hartenberg (D-H) algorithm cannot be directly applied for developing continuum arm kinematics. Moreover, the design of each continuum arm varies with respect to the flexible backbone present in the system, the positioning, type and number of actuators. The constraints imposed by these factors make the set of reachable configurations and nature of movements unique to every continuum robot. This makes it difficult to formulate generalized kinematic or dynamic models for continuum robot hardware. Thus, the kinematics (i.e. geometry based modeling) of a quite general set of prototypes of continuum manipulators has been developed and basic control strategies now exist based on these. The development of analytical models to analyze continuum arm dynamics (i.e. physics based models involving forces in addition to geometry) is an active, ongoing research topic in this field. From a practical perspective, the modeling approaches currently available in the literature prove to be very complicated and a dynamic model which could be conveniently implemented in an actual device’s real-time controller has not been developed yet. The absence of a computationally tractable dynamic model for these robots also prevents the study of interaction of external forces and the impact of collisions on these continuum structures. This impedes the study and ultimate usage of continuum robots in various practical applications like grasping and manipulation, where impulsive dynamics [4-10] are important factors. Although continuum robotics is an interesting subclass of robotics with promising applications for the future, from the current state of the literature, this field is still in its stages of inception.

Controller (control system) is a device which can sense information from linear or nonlinear system (e.g., robot arm) to improve the systems performance and the immune system behavior [11-20]. In feedback control system considering that there are many disturbances and also variable dynamic parameters something that is really necessary is keeping plant variables close to the desired value. Feedback control system development is the most important thing in many different fields of safety engineering. The main targets in design control systems are safety stability, good disturbance rejection to reach the best safety, and small tracking error[21-33]. At present, in some applications robot arms are used in unknown and unstructured environment, therefore strong mathematical tools used in new control methodologies to design nonlinear robust controller with an acceptable safety performance (e.g., minimum error, good trajectory, disturbance rejection). According to the control theory, systems’ controls are divided into two main groups: conventional control theory and soft computing control theory. Conventional control theories are work based on manipulator dynamic model. This technique is highly sensitive to the knowledge of all parameters of nonlinear robot manipulator’s dynamic equation. Conventional control theory is divided into two main groups: linear control theory and nonlinear control theory. Soft computing (intelligent) control theory is free of some challenges associated to conventional control theory. This technique is worked based on intelligent control theory. This theory is divided into the following groups: fuzzy logic theory, neural network theory, genetic algorithm and neuro-fuzzy theory.

Advanced control techniques such as integrator backstepping, feedback linearization, adaptive and robust have been applied to the control of numerous single- axis machines and robotic manipulators. Since available control techniques for continuum robot and robotic manipulators are so broad, the review in this research is restricted to some of the nonlinear control techniques for continuum robot. Most of the authors referenced on the nonlinear control techniques for continuum robot also do a significant amount of work on the control of robotic manipulators. Kokotovic [13] published one of the pioneering works on the backstepping control technique and Qu et al. [14] extended this technique and developed a robust backstepping-type controller for a one-link robot with the motor dynamics taken into consideration. Carroll et al. [15] also extended the work of Kokotovic [16] to design an embedded computed torque and output feedback controller for pennanent magnet brush de (BDC) motors. Hemati et al. [16] developed a robust feedback linearizing controller for a single-link robot actuated by a brushless de motor (BLOC). In [17], Carroll et al. also developed a robust tracking controller for a BLOC, which achieved globally bounded results for rotor position tracking error despite parametric uncertainties and additive bounded disturbances. In addition to DC machines, SR and PM stepper motors are also candidates for advanced nonlinear controllers. In [18], Die'-Spong et al. introduced a detailed nonlinear model and an electronic commutation strategy for the SR motor and applied a state feedback control algorithm which compensated for all the nonlinearities of the system. The work in [18]

was then generalized to a direct-drive manipulator with SR actuation by Taylor et al. [19]. Carroll et al. [20] also used a backstepping technique to develop an adaptive tracking controller for the SR motor. Bodson [21] developed a model-based control law for the PM stepper motor using an exact linearization methodology while considering practical issues such as voltage saturation. Even though some of the above control techniques are not of the backstepping type controller, the backstepping-type controller developed in this thesis was somewhat inspired by them.

Although the fuzzy-logic control is not a new technique, its application in this current research is considered to be novel since it aimed for an automated dynamic-less response rather than for the traditional objective of uncertainties compensation[38-60]. The intelligent tracking control using the fuzzy-logic technique provides a cost-and-time efficient control implementation due to the automated dynamic-less input. This in turn would further inspire multi-uncertainties testing for continuum robot [38-60]. In project we can used fuzzy logic theory when a plant can be considered as a black box with outputs available for measurement and a possibility of changing inputs. The plant is supposed to be observable and controllable. Some information about the plant operation or plant control is available, which can or cannot be of a quantitative nature, but it can be formulated as a set of rules (maybe after some processing). An acceptable fuzzy control solution is possible, which should satisfy design specifications. It must not be optimal in regard to some criteria as it is hard to prove that a fuzzy control system is optimal and even stable. However, a fuzzy controller is able to provide a stable and ‘good’ solution.

This method is based on design PID like fuzzy controller based on the minimum rule base and applied this controller to conventional backstepping controller to solve the robust challenge in backstepping controller and have a linear behavior based on the nonlinear control system.

This paper is organized as follows; section 2, is served as an introduction to the dynamic of continuum robot, backstepping controller, design linear PID controller and fuzzy inference system. Part 3, introduces and describes the methodology algorithm. Section 4 presents the simulation results and discussion of this algorithm applied to a continuum robot and the final section describe the conclusion.

• II.    THEORY

Dynamic Formulation of Continuum Robot: The Continuum section analytical model developed here consists of three modules stacked together in series. In general, the model will be a more precise replication of the behavior of a continuum arm with a greater of modules included in series. However, we will show that three modules effectively represent the dynamic behavior of the hardware, so more complex models are not motivated. Thus, the constant curvature bend exhibited by the section is incorporated inherently within the model. The model resulting from the application of Lagrange’s equations of motion obtained for this system can be represented in the form

^coeff = (q) ̈+c(q) ̇+G(9 ) (1)

where T is a vector of input forces and q is a vector of generalized co-ordinates. The force coefficient matrix ^coeff transforms the input forces to the generalized forces and torques in the system. The inertia matrix, D is

composed of four block matrices. The block matrices that correspond to pure linear accelerations and pure angular accelerations in the system (on the top left and on the bottom right) are symmetric. The matrix C contains coefficients of the first order derivatives of the generalized co-ordinates. Since the system is nonlinear, many elements of C contain first order derivatives of the generalized co-ordinates. The remaining terms in the dynamic equations resulting from gravitational potential energies and spring energies are collected in the matrix G . The coefficient matrices of the dynamic equations are given below,

= ⎢⎢ ⎢ ⎢		⎡1       1          ( 91 ) 00  1 00  0 1⁄2  -1⁄2   1⁄2 0     0     1⁄2 00  0		( 91 ) 1 0 -1⁄2 -1⁄2 0	( 9i + 92 ) ( e2 ) 1 1⁄2+ s2sin ( e2 )- 1⁄2 1⁄2	( 91 + 62 ) ( e2 ) 1 1⁄2+ s2sin ( 92 ) -1⁄2 -1⁄2     ⎦	⎥⎥ ⎥
D( )=		⎡       + m2 ⎢+		m2cos ( 9i ) 2        Л тп3 cos (  +   ) + m3cos ( 9i )		-         ( ®i ) - m3s2sin ( 9i)-m3s3stn( 9i + 92 ) -         ( 9i + 9г )		0	⎥⎥ ⎥
		⎢     m2cos (9i) ⎢+ m3cos ( 9i )		m2 +	m3 cos ( »2 )	-     ( e2 )- m3s3sin ( »2 )		0	⎥⎥
		⎢ m3cos (9i + 92 )		m3 cos ( »2 )	m3	m3s3stn( e2	)0	0	⎥⎥
		⎢ ⎢-m2s2stn( 9i ) ⎢- m3s2sin ( 9i ) ⎢- m3s3sin ( 9i + 92 )		-        ( 92 )   m3s2stn( 92 )		m2s^ + к + +    + + к + m3s^ + + пт3 S3COS ( 92 ) s2 +2 *n3 S3COS ( 92 ) s2			⎥⎥ ⎥⎥
		⎢ - m3s3sin ( 9i + ^2 )		-   ( 92)0		'2 + m3s^ +   .      I +      + , + m3s3cos ( 92 )          +     +		к	⎥ ⎥⎥
		⎣	0	0	0	к	к	h ⎦	⎥
c( 4 )=	⎢⎢⎡ ⎢⎢⎢⎢              +		-2 m2sin (9i)6̇    - -2m3stn( 9i )6̇		2m3stn( 9i + 92 ) ( ̇+ ̇)	- ( 9i )( t ̇) +(1⁄2)( Cll + c2i ) -            -        ( 9i + 92 ) ( 9i )( t ̇ ) - ( 9i + 62)( t ̇)		⎤ ⎥ 0⎥ ⎥⎥ ⎥⎥
	⎢⎢⎢⎢⎢⎢                              0		C12 + c22		-2m3stn(92 ) ( ̇+ ̇)	-     (£ ̇) +(1⁄2) ( C12 +    ) -      ( t ̇) - ( »2)( t ̇)	-2 ( e2 )( t ̇) - ( fl2)( t ̇ )	⎥ 0 ⎥⎥
	⎢⎢⎢⎢                    0		2 m3sm ( e2 )(6̇ )		C13 + C23	- ( 62)( t ̇) -      ( t ̇)	-2      ( t ̇ ) -      ( t ̇)        (	⎥ (1⁄2)   ⎥ +    )⎥
	⎢   (1⁄2) ( C11 +    )		2 m3s3cos ( »2)( ̇) -2 m3s2 ( t ̇ ) +2 m2s2 ( t ̇ )		2      (6̇ +6̇) -2 *n3 s2 cos ( »2 ) (6̇ +6̇)	2 m3s3s2 ( 62)( t ̇ ) +(1 ⁄4) ( Сц +   )	m3s3s2 ( 62)( t ̇ )	⎥ 0 ⎥⎥
	⎢⎢            0		(1⁄2)(C12 + c22)+ 2 713 S3COS ( »2)( ̇)		2 (6̇ +6̇)	m3s3s2 ( 92 )( t ̇ )	(1 ⁄4) ( c12 + c22 )	⎥⎥ 0            ⎥⎥
	⎣0		0		(1⁄2)(C12 -   )	0	0 (	⎥ (1 ⁄4)  ⎥ +    )⎦

^G( 1 )=

- т_гд -    + ku (Si + (1⁄2)9i -   )+ ku (si-(1⁄2)9i -   )- m₃g

-       ( 91)+ k_u (s₂ + (1⁄2)9₂ -   )+ ku (s₂ - (1⁄2)9₂ -   )- m₃gcos (9i)

-       (9i + 9₂)+ ku (s₃ + (1⁄2)9₃ -   )+ k₂₃ (s₃ - (1⁄2)9₃ -   )

m₂s₂gsm ( 9i )+ m₃s₃gsin ( 9i + 9₂ )+ m₃s₂gsin ( 9i )+ ku ( Si +(1⁄2) 9i -   )(1⁄2)

+ ku (Si - (1⁄2)9i -   _{)(-1⁄ 2 )}

m₃s₃gsin (9i + 6₂ )+ ku (s₂ + (1⁄2) 6₂ -   )(1⁄2) + k₂₂ (s₂-(1⁄2) 6₂ -   )(-1⁄2)

⎣          ku (s₃ + (1⁄2)9₃ -   )(1⁄2) + ku (s₃-(1⁄2)9₃ -   )(-1⁄2)

Backstepping Controller: The continuum robot dynamics in (1) have the appropriate structure for the so-called backstepping controller design method. With the position error defined as ^1 = - , all joints will track the desired specified state X^ if the error dynamics are given as follows:

(Ż 1+[Kp]Z1)=0                  (6)

where [K p ] is a positive definite gain matrix. The error dynamics in (6) can be rewritten as:

Х2 =Х̇ 1 +[Kp]Z 1                  (7)

Substitution of (7) into (1) makes the position error dynamics go to zero. Since the state vector x2 is not a control variable, (7) cannot be directly substituted into (1). The expression in (7) is therefore defined as a fictitious control input and is labeled expressed below as Х2 .

Х2d =Х̇id+[Kp](Хd -Х )            (8)

The fictitious control input in (8) is selected as the specified velocity trajectory and hence the velocity error can be defined as Z2 =Х2 d -Х2 . With the following dynamics

(Ż 2+[Kp]Z2)=0                   (9)

the joint position error will approach zero asymptotically, which will lead to the eventual asymptotic convergence of the joint position error. The error dynamics in (9) can be rewritten as:

Х2 =Х̇d+[Kp]Z2

Substitution of (9) into (1) leads to the following expression as the desired stabilizing torque:

τ=[Η](Х̇2d+[Kp]Z2)+C(Х1,Х2)      (11)

The desired torque control input is a nonlinear compensator since it depends on the dynamics of the spherical motor. The time derivative of desired velocity vector is calculated using (9). In terms of the desired state trajectory, and its time derivatives and the position and velocity state variables, the desired torque can be rewritten in following form:

τ=[Η]y+C(Х1,Х2)              (12)

Where y=ẌId+([Kp]+[Kd])(Ẋ Id -      (13)

Х̇ 1)+([Kp][Kd]Хd -Х

The backstepping controller developed above is very similar to inverse dynamics control algorithm developed for robotic manipulators. The backstepping controller is ideal from a control point of view as the nonlinear dynamics of the continuum robot are cancelled and replaced by linear subsystems. The drawback of the backstepping controller is that it requires perfect cancellation of the nonlinear continuum robot dynamics. Accurate real time representations of the robot dynamics are difficulty due to uncertainties in the system dynamics resulting from imperfect knowledge of the robot mechanical parameters; existence of unmodeled dynamics and dynamic uncertainties due to payloads. The requirement for perfect dynamic cancellation raises sensitivity and robustness issues that are addressed in the design of a robust backstepping controller. Another drawback of the backstepping controller is felt during real-time implementation of the control algorithm. Implementation of the backstepping controller requires the computation of the exact robot dynamics at each sampling time. This computational burden has an effect on the performance of the control algorithm and imposes constraints on the hardware/software architecture of the control system. By only computing the dominant parts of the robot dynamics, this computational burden can be reduced. These drawbacks of the backstepping controller makes it necessary to consider control algorithms that compensate for both model uncertainties and for approximations made during the on-line computation of robot dynamics. The next section provides robust modifications of the backstepping controller described in this section. Figure 1 shows the block diagram of backstepping controller

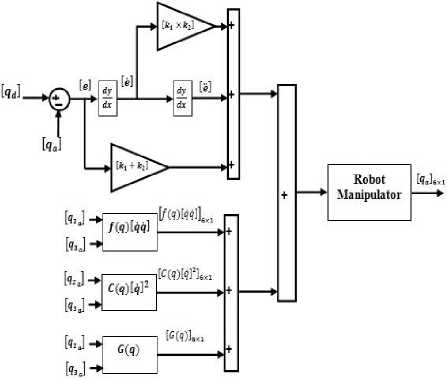
Fig 1: Block diagram of robust backstepping controller

Robust Backstepping Control: When there are uncertainties in the spherical motor dynamics due to modeling inaccuracy and computational relaxation, robust controllers are ideal for ensuring system stability. When the system dynamics are completely known, the required torque control vector for the control of the spherical motor is given by (12) and (13). In the presence of modeling uncertainties, a reasonable approximation of the torque control input vector is given by у = Л^ + ([^] + М(^ - ХО +

(№]Х d-xa

Td = [£]у + С where [jtf] and С are estimates of the inertia and coriolis terms in the spherical motor dynamics; and у is given by (13). The uncertainty on the estimates are expressed as

[н] = [Я] - [я]

^(m-ra-^Dy-Dtfrc

Substitution of (14) for у in (19) results in the following expression for the closed loop error dynamics.

Ж1 + ([Kp] + [KdM + [Kp] [№ = ^

Defining a new error state vector,

и

the error dynamics in (21) can be expressed as

£=[ГК+[О](^-у + ч) ⁽²³⁾

Where ^[F^] = [[0] [1]] and ^[D^] = [[0]] are block matrices of dimensions R^6X6 and r ^6x3 respectively. Since П is a nonlinear function of the position and velocity state vectors, the system error dynamics in the above equation are nonlinear and coupled. The backstepping controller developed in the previous section cannot guarantee system stability. The Lyapunov direct method is, however, used to design an outer feedback loop on the error dynamics that compensates for the system uncertainty contributed by n.

Fuzzy Logic Controller: Based on foundation of fuzzy logic methodology; fuzzy logic controller has played important rule to design nonlinear controller for nonlinear and uncertain systems [33]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of;

Input fuzzification (binary-to-fuzzy [B/F] conversion)

Fuzzy rule base (knowledge base), Inference engine and Output defuzzification (fuzzy-to-binary [F/B] conversion). Figure 2 shows fuzzy controller operation.

[ c] = [C]-[C]                      (17)

These uncertainties account for both imperfect modeling and intentional computational simplification. Application of the approximate control vector given by (15) leads to the following expression for the closed loop dynamics:

[O 2 + С = [% + C           (18)

Since the inertia matrix [H] is symmetric and positive definite, the closed loop dynamics in (18) can be rewritten as

% i =y-^ ⁽¹⁹⁾

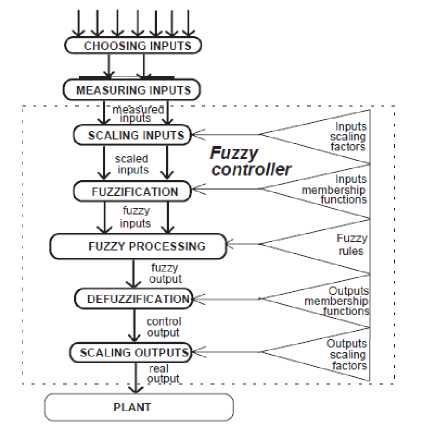
Fig 2: Fuzzy Controller operation

Where

The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy controllers to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno use a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base if x is A and у is В then z is C 'mamdani'          (24)

if x is A and у is В then z is f(x, y) 'sngeno'

When x and y have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation ( AND/OR ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Two most common methods that used in fuzzy logic controllers are Max-min aggregation and Sum-min aggregation. Maxmin aggregation defined as below;

(   ,    ,   ) = ⋃        (   ,    , )(25)

=max,min *    (  ,  ),    ()+-

The Sum-min aggregation defined as below

(   ,    ,   ) =   ⋃        (   ,    ,   )(26)

=∑min *    (  ,  ),   ()+ where is the number of fuzzy rules activated by and and also ( , , ) is a fuzzy interpretation of - ℎ rule. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method ( ) and Centre of area method ( ) are two most common defuzzification methods, which method used the following equation to calculate the defuzzification

(    ,     )

∑     ∑    ․    (   ,   ,   )

∑∑   ․   (  ,   ,  )

and     method used the following equation to calculate the defuzzification

(   ,    )

∑     ․     (   ,    ,    )

∑    .(  ,   ,   )

Where COG(x ,y ) and COA(x ,y ) illustrates the crisp value of defuzzification output, U ∈ U is discrete element of an output of the fuzzy set, µ . (x ,y ,U ) is the fuzzy set membership function, and r is the number of fuzzy rules.

Design PID Controller: Design of a linear methodology to control of continuum robot manipulator was very straight forward. Since there was an output from the torque model, this means that there would be two inputs into the PID controller. Similarly, the outputs of the controller result from the two control inputs of the torque signal. In a typical PID method, the controller corrects the error between the desired input value and the measured value. Since the actual position is the measured signal. Figure 3 shows linear PID methodology, applied to continuum robot manipulator [21-34].

()=  ()-  ()                (29)

=   +   ̇+ ∑

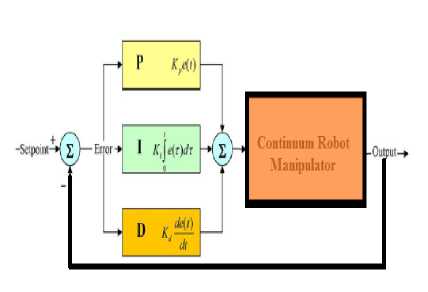
Fig 3: Block diagram of linear PID method

The model-free control strategy is based on the assumption that the joints of the manipulators are all independent and the system can be decoupled into a group of single-axis control systems [18-23]. Therefore, the kinematic control method always results in a group of individual controllers, each for an active joint of the manipulator. With the independent joint assumption, no a priori knowledge of robot manipulator dynamics is needed in the kinematic controller design, so the complex computation of its dynamics can be avoided and the controller design can be greatly simplified. This is suitable for real-time control applications when powerful processors, which can execute complex algorithms rapidly, are not accessible. However, since joints coupling is neglected, control performance degrades as operating speed increases and a manipulator controlled in this way is only appropriate for relatively slow motion [44, 46]. The fast motion requirement results in even higher dynamic coupling between the various robot joints, which cannot be compensated for by a standard robot controller such as PID [50], and hence model-based control becomes the alternative.

• III.    Methodology

Conversely pure backstepping controller is a high-quality nonlinear controller; it has an important problem; nonlinear equivalent dynamic formulation in uncertain dynamic parameter and partly uncertain system. Backstepping controller is a nonlinear controller but it has a challenge in stability and robustness in presence of uncertainty and external disturbance. Based on literature backstepping dynamic formulation is written by;

т = (ё + (KY х К)ё + (KY + Юе)     (31)

+ N(q,q')

The main challenge in this research is the role of nonlinearity term in presence of uncertainty. To solve this main challenge artificial intelligence based controller is introduce. This type of controller is intelligent therefore design a dynamic of system based on experience knowledge is done by this method. One of the main artificial intelligence techniques is fuzzy logic theory. In this theory the behavior and dynamic of controller is defined by rule base. However defined and number of rule base play important role to design high quality controller but system has limitation to the number of rule base to implementation and the speed of response. Based on literature PID controller can reduce or eliminate the steady state error and design stable controller. But this type of controller has three types of inputs; proportional part, integral part and derivative part. To design PID like fuzzy controller and if any input is described with seven linguistic values, and any rule has three conditions we will need 7 × 7 × 7 = 343 rules. It is too much work to write 343 rules, the speed of system is too low and design embedded controller based on FPGA or CPLD is very difficult. Based on (9) the PID controller has three inputs and three coefficients. In PD like fuzzy controller error and change of error are the inputs and if any input is described with seven linguistic values, and any rule has two conditions we will need 7 × 7= 49 rules. Table 1 shows the rule table of PD like fuzzy controller based on seven linguistic variables for each input and totally 49 rules.

Table 1: Rule Table of PD like Fuzzy Controller

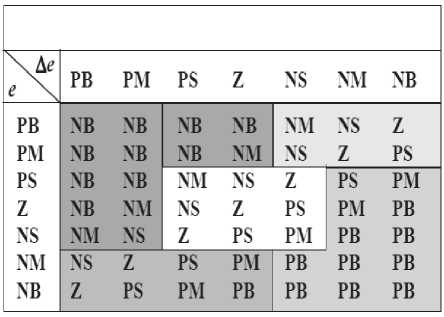
This table includes 49 rules. We are taking into account now not just the error but the change-of-error as well. It allows describing the dynamics of the controller. To explain how this rules set works and how to choose the rules, let us divide the set of all rules into the following five groups:

Group 1: In this group of rules both e and Ae are (positive or negative) small or zero. This means that the current value of the process output variable has deviated from the desired level (the set-point) but is still close to it. Because of this closeness the control signal should be zero or small in magnitude and is intended to correct small deviations from the set-point. Therefore, the rules in this group are related to the steady-state behavior of the process. The change-of-error, when it is Negative Small or Positive Small, shifts the output to negative or positive region, because in this case, for example, when e(t) and Ae(t) are both Negative Small the error is already negative and, due to the negative change-of-error, tends to become more negative. To prevent this trend, one needs to increase the magnitude of the control output.

Group 2: For this group of rules e(t) is Positive Big or Medium which implies that actual input is significantly above the set point. At the same time since Ae(t) is negative, this means that actual input is moving towards the set-point. The control signal is intended to either speed up or slow down the approach to the set-point. For example, if actual input is much below the set-point (e(t) is Positive Big) and it is moving towards the set-point with a small step ( Ae(t) is Negative Small) then the magnitude of this step has to be significantly increased (U is Negative Medium). However, when actual input is still much below the set-point (e(t) is Positive Big) but it is moving towards the set-point very fast (Ae(t) is Negative Big) no control action can be recommended because the error will be compensated due to the current trend.

Group 3: For this group of rules actual output is either close to the set-point ( e(t) is Positive Small, Zero, Negative Small) or significantly above it (Negative Medium, Negative Big). At the same time, since Ae(t) is negative, actual input is moving away from the set-point. The control here is intended to reverse this trend and make actual input, instead of moving away from the setpoint, start moving towards it. So here the main reason for the control action choice is not just the current error but the trend in its change.

Group 4: For this group of rules e(t) is Negative Medium or Big, which means that actual input is significantly below the set-point. At the same time, since Ae(t) is positive, actual input is moving towards the setpoint. The control is intended to either speed up or slow down the approach to the set-point. For example, if actual input is much above the set-point (e(t) is Negative Big) and it is moving towards the set-point with a somewhat large step (Ae(t) is Positive Medium), then the magnitude of this step has to be only slightly enlarged (output is Negative Small).

Group 5: The situation here is similar to the Group 3 in some sense. For this group of rules e(t) is either close to the set-point (Positive Small, Zero, Negative Small) or significantly above it (Positive Medium, Positive Big). At the same time since Ae(t) is positive actual input is moving away from the set-point. This control signal is intended to reverse this trend and make actual input instead of moving away from the set-point start moving towards it. The PD like fuzzy controller shows in Figure 4.

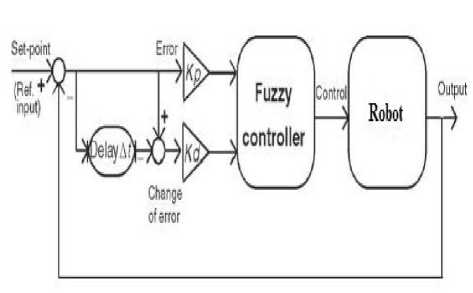
Fig 4: Block diagram of PD like Fuzzy Controller

In PI like controller error and integral of error are the inputs. We can integrate the output of a controller, not the input. Then we may have the error and the change of error inputs and still realise the PI-control. Based on above discussion the PID-like fuzzy controller can be constructed as a parallel structure of a PD-like fuzzy controller and a PI-like controller (Fig. 5) with the output approximated as:

U_PiD =VT^e+^{K v}a ⁶

j + (K^e + K i £e)

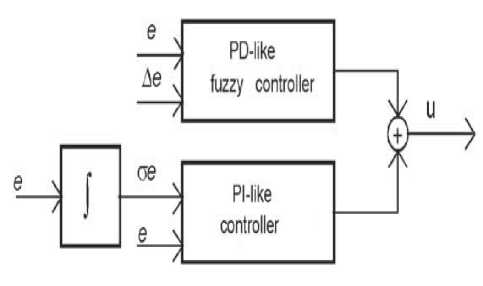
Fig 5: the structure for a PID-like fuzzy controller

In this type of design, we have 49 rule bases for PD like fuzzy controller. This PID like fuzzy controller applied to pure backstepping controller to remove the challenge in this conventional nonlinear controller. Figure 6 shows the block diagram of PID like fuzzy backstepping controller.

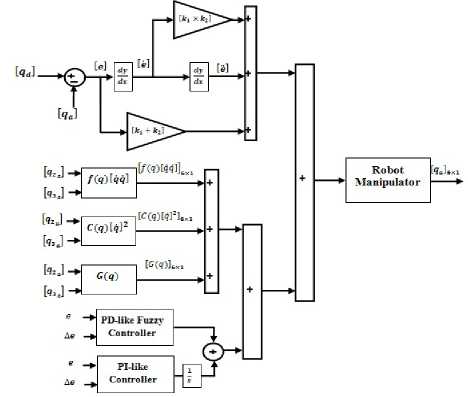
Fig 6: Block diagram of PID like Fuzzy Backstepping Controller

• IV.    RESULTS AND DISCUSSION

PID like fuzzy backstepping controller was tested to Step response trajectory. In this simulation, to control position of continuum robot without and with external disturbance. The simulation was implemented in MATLAB/SIMULINK environment. These systems are tested by band limited white noise with a predefined 40% of relative to the input signal amplitude. This type of noise is used to external disturbance in continuous and hybrid systems and applied to nonlinear dynamic of these controllers.

Tracking performances: In proposed controller; the performance is depended on two important parameters; nonlinear equivalent part and PID like fuzzy controller. According to above discussion PID like fuzzy backstepping controller and pure backstepping controller have the same performance in certain system. Based on Fig 7, pure backstepping controller has a slight transient oscillation, to solve this challenge the output gain updating factor of PID like fuzzy backstepping controller is decreased.

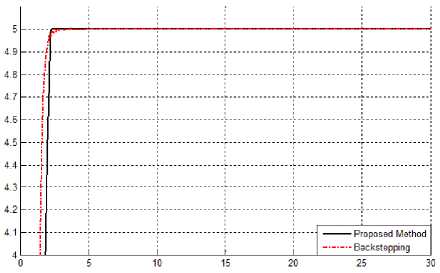
Fig 7: Backstepping controller and proposed method

Disturbance rejection: Figure 8 shows the power disturbance elimination in proposed method and pure backstepping controller in presence of external disturbance and uncertainty parameters. The disturbance rejection is used to test and analyzed the robustness comparisons of these controllers for step trajectory. A band limited white noise with predefined of 40% the power of input signal value is applied to the step trajectory. According to the following graph, pure backstepping controller has moderate fluctuation in presence of external disturbance and uncertainty.

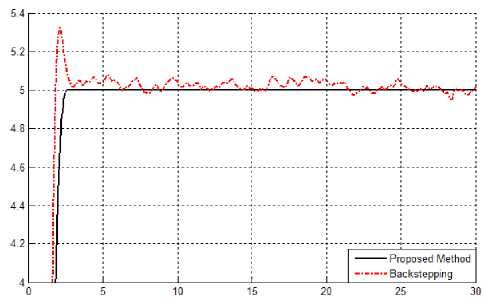
Fig 8: Backstepping controller and proposed method in presence of external disturbance

According to above graph, conventional backstepping has overshoot and oscillation in presence of external disturbance.

• V.    CONCLUSION

The central issues and challenges of nonlinear control and estimation problems are to satisfy the desired performance objectives in the presence of noises, disturbances, parameter perturbations, un-modeled dynamics, sensor failures, actuator failures and time delays. Evaluation algorithm PID like fuzzy backstepping controller has shown growing popularity in both industry and academia. To improve the optimality and robustness, we have proposed PD like fuzzy controller parallel with PI like controller based on 49 rule base for nonlinear systems with general performance criteria. Backstepping controller provides us an effective tool to control nonlinear systems through the dynamic formulation of nonlinear system. Fuzzy logic controller is used to estimate highly nonlinear dynamic parameters. Mixed performance criteria have been used to design the controller and the relative weighting matrices of these criteria can be achieved by choosing different coefficient matrices. The simulation studies show that the proposed method provides a satisfactory alternative to the existing nonlinear control approaches.

ACKNOWLEDGMENT

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the

SSP Institute of Advance Science and Technology Program of Iran under grant no. 2013-Persian Gulf-2A.