Design Novel Model Reference Artificial Intelligence Based Methodology to Optimized Fuel Ratio in IC Engine

Published Online August 2013 in MECS (http://www.

Automotive internal combustion (IC) engines are designed to produce power from the energy that is contained in their fuel. More specifically, their fuel contains energy and together with air, this mixture ignites to output useable mechanical power. There are several types of fuels as well as combustion types that can be used in automotive IC engines, all of which must be controlled to optimize the fuel that is used by the engine, maximize the power that will be used to operate the vehicle, and reduce the harmful gases that are produced from the combustion. As discussed in the previous research, control systems engineering applications employ the use of engine models to aid in controls design, optimization and evaluation [1-3]. For performance applications, the one-dimensional simulation technique has become the industry standard, while for large scale control studies and optimizations, the zero dimensional cycle resolve model is the prevalent choice. In developing a valid engine model of spark-ignition engines, the concept of the combustion process must be understood. The combustion process is relatively simple and it begins with fuel and air being mixed together in the intake manifold and cylinder. This air-fuel mixture is trapped inside the cylinder after the intake valve(s) is closed and then gets compressed [4-8]. Air-to-fuel (A/F) ratio is the mass ratio of air and fuel trapped inside the cylinder of an engine before combustion starts. When all of the fuel in the cylinder is combined with all of the oxygen in the combustion chamber (cylinder), the mixture of air and fuel is a stoichiometric mixture [9-10].There are two basic methods of dealing with control problems, the linear methodology and the nonlinear methodology. Strictly speaking, linear systems do not exist in practice, since all physical systems are nonlinear. However, the great majority of control algorithms are designed assuming linear behavior [11]. To make linear methodologies work, the key assumption is to assume a linear characteristics over a small range of operation. This enables the designer to obtain a linearized version of a nonlinear system model. But, there are numerous control situations in which the linear control system fails to meet the requirements, for instance, systems with large parameter variations or when the state of the system is far from the linearization point [12-15]. The parameter variations and nonlinearities can degrade system performance and possibly destabilize the system. In addition, the nonlinearities called hard nonlinearities, such as motor pressure, engine angular speed saturation, matrix mass of air in cylinder and large variations in loads and tasks. Possess discontinuous features that do not lend themselves to linear approximation. Usually, such nonlinear characteristics have undesirable effects on the performance of the systems under investigation and control systems have to be designed to compensate for them. Considering linear and nonlinear control methodologies the nonlinear ones are more general since they can be successfully applied to linear systems whereas a linear controller might be insufficient for control of a nonlinear system [16-20]. It is worthy to note that, .more recently, there has been a growing interest among researchers in new types of controllers which can combine the approximation power of computational-intelligence techniques (e.g., fuzzy logic and neural networks) with the simplicity of the most commonly used linear controller called three-term or proportional-integral-derivative (PID) controller [21-24]. The complexity of nonlinear uncertain systems challenges a control system designer to come up with a unified systematic design procedure to meet the control objectives (e.g., stability and robustness) and design specifications. Faced with such challenges, an investigation of different nonlinear uncertain systems has made it clear that the designer cannot expect one particular procedure be applicable to all nonlinear uncertain systems [25-29]. A multitude of nonlinear control laws have been developed called "computed-fuel ratio " or "inverse dynamic" controller in the IC engine literature. These controllers incorporate the inverse dynamic model of IC engine to construct model-based controller. The computed fuel ratio controllers have their root in feedback linearization control methodology. The idea is to design a nonlinear feedback (maybe calculated using the inverse dynamic model of the IC engine to be controlled) which cancels the nonlinearities of an actual IC engine. In this manner the closed-loop system becomes exactly linear or partly linear depending on the accuracy of the dynamic model, and then a linear controller such as PD and PID can be applied to control the IC engine [30-31]. Due to the fact that parameters errors are not the sole source of imperfect decoupling and linearization of the IC engine dynamics, thus this control methodology cannot provide robustness against external unstructured uncertainties. Another difficulty that may be encountered in the implement of computed-Fuel ratio control is that the entire dynamic model (the mass of air matrix, the pressure of motor, engine angular speed and mass of air in cylinder) of the IC engine, since control is now based on the nonlinear feedback of the current system state. For an IC engine these computations can be complicated and time consuming. The problem of computation burden can even be increased when the adaptive computed-fuel ratio control is used. This is due to extra computation needed to update the parameters in each sample time. Two methods can be found in the literature to deal with the problem of computation burden described above. One method to deal with the problem of computation burden is to use feed forward computed-fuel ratio control in which the PFI and DI vectors are computed on the basis of the desired measure of the fuel and computed-fuel ratio compensates the nonlinear coupling effects [18-19]. As opposed to feedback computed-fuel ratio control, in the feedforward method it is possible to pre-compute all the terms of the dynamic model off-line and reduce the computation burden to a large extent. The second method to deal with the problem of heavy computation burden in the computed-fuel ratio control is to develop a computationally efficient dynamic model by mass of air in PD method. As mentioned in above, the IC engines are inherently complex and nonlinear uncertain systems with human-like behavior [10-12]. Since fuzzy systems are able to mimic the human approach for controlling and optimizing the systems, these systems can be a valuable tool for modeling the Complex dynamics or inverse dynamics of IC engine in order 10 build a model-based robust controller. Very often tile approximation capabilities of the fuzzy systems are used for compensating the unknown dynamics or particular component of the dynamics of a system. Therefore, the goal is to develop a controller similar to the human brain. Based on the extensive literature review it was found that various controls with various control methodologies to reduce the error. The combination not only encompasses the features and capabilities of its components (i.e., different control methodologies) but also the limitations attributed to these techniques may be remedied by each other. Therefore, a combined nonlinear robust control methodology is selected to deal with the control of IC engine in the presence of uncertainties. The research described in this paper focuses on the synthesis, design, analysis (i.e., stability and robust analysis) and implementation of this combined nonlinear robust controller. The robust is selected as a framework to synthesize the controller, since the PD plus mass of air methodologies have proven very effective in a variety of practical control of, IC engines [1-8].

One of the most significant challenges in control algorithms is a linear behavior controller design for nonlinear systems (e.g., IC engine). Some of IC engines are controlled by linear PID controllers, but the designs of linear controller for these systems are extremely difficult because they are hardly nonlinear and uncertain. To reduce the above challenges, the nonlinear robust controller is used to control of IC engine. PD plus mass of air is a nonlinear controller. Parallel fuzzy PD plus mass of air controller is used to control of highly nonlinear systems especially for IC engines. Estimate nonlinear equivalent dynamic formulation in uncertain dynamic parameter is the main drawback in pure PD plus mass of air controller. The nonlinear equivalent dynamic formulation problem in uncertain system is solved by using fuzzy logic theorem. Fuzzy logic theory is used to estimate the system’s dynamics. This methodology is based on applied fuzzy logic in PD plus mass of air to estimate the nonlinear term of IC engine.

This paper is organized as follows: In section 2, main subject of modeling IC engine formulation and fuzzy logic method are presented. Detail of proposed methodology is presented in section 3. In section 4, the simulation result is presented and finally in section 5, the conclusion is presented.

II.    THEORY 2.1    Case study:Dynamic Formulation of IC Engine

Dynamic equation is the study of motion with regard to forces. Dynamic modeling is vital for control,

46          Design Novel Model Reference Artificial Intelligence Based Methodology to Optimized Fuel

Ratio in IC Engine

mechanical design, and simulation. It is used to describe dynamic parameters and also to describe the relationship between PFI and DI to force acting on IC engine. Several different methods are available to compute IC engine dynamic equations. These methods include the Newton-Euler (N-E) methodology, the Lagrange-Euler (L-E) method, and Kane’s methodology [1]. The Newton-Euler methodology is based on Newton’s second law and several different researchers are signifying to develop this method [1, 14]. This equation can be described the behavior of a IC engine step by step, called forward recursion and transfer the essential information from PFI and DI to fuel ratio, called backward recursive. The literature on Euler-Lagrange’s is vast but a good starting point to learn about it is in[1]. Calculate the dynamic equation IC engine using E-L method is easier because this equation is derivation of nonlinear coupled and quadratic differential equations. The Kane’s method was introduced in 1961 by Professor Thomas Kane[1, 6]. This method used to calculate the dynamic equation of motion without any differentiation between kinetic and potential energy functions.

Dynamic modeling of IC engine is used to describe the nonlinear behavior of IC engine, design of model based controller such as pure variable structure controller based on nonlinear dynamic equations, and for simulation. The dynamic modeling describes the relationship between fuel to air ratio to PFI and DI and also it can be used to describe the particular dynamic effects (e.g., motor pressure, angular speed, mass of air in cylinder, and the other parameters) to behavior of system[1].

The equation of an IC engine governed by the following equation [1-4]:

ГPFI1    Г^М air 11    Ml air 12] [FR1  , [P motor 11 r„.„ . 1 ,

I DI J = к „,,   Й . I¹ J ⁺ P R " ' 1 ⁺

N 11 N 12     FR ^{2   M} a1

К N ,, 1 ^{X 1} d i 1 + ¹M a ₂ J                       (1)

Where PFI is port fuel injector, DI is direct injector, M_air is a symmetric and positive define mass of air matrix, P_motor is the pressure of motor, N is engine angular speed and M_a is matrix mass of air in cylinder. Fuel ratio and exhaust angle are calculated by [2,5, 9]:

I 9=

^Mair 11

M.

-1

air 12

■ ^Mair 21

M air 22

Iffl-lfTli"......

ui         motor 2^J

+

" Nn

^N 12

- N21

^N 22

The above target equivalence ratio calculation will be combined with fuel ratio calculation that will be used for controller design purpose.

2.2 Fuzzy Logic Methodology

Zadeh introduced fuzzy sets in 1965. After about 50 years, fuzzy systems have been widely used in different fields, especially on control problems. Fuzzy systems transfer expert knowledge to mathematical models. Fuzzy systems use fuzzy logic to estimate dynamics of our systems. Fuzzy controllers including fuzzy if-then rules are used to control IC engines [1620]. Conventional control methods use mathematical models to control systems. Fuzzy control methods replace the mathematical models with fuzzy if-then rules and fuzzy membership functions to control systems. Both fuzzy and conventional control methods are designed to meet system requirements of stability and convergence. When mathematical models are unknown or partially unknown, fuzzy control methods can use fuzzy systems to estimate the unknown models. This is called the model-free approach. Conventional control methods can use adaptive control methods to achieve the model free approach. When system dynamics become more complex, nonlinear systems are difficult to handle, by conventional control methods. From the universal approximation theorem in below, fuzzy systems can approximate arbitrary nonlinear systems [21-23].

SUP xeu V (x) -g (x)|< e                       (3)

In practical problems, systems can be controlled perfectly by experts. Experts provide linguistic description about systems. Conventional control methods cannot design controllers combined with linguistic information. When linguistic information is important for designing controllers, we need to design fuzzy controllers for our systems. Fuzzy control methods are easy to understand for designers. The design process of fuzzy controllers can be simplified with simple mathematical models. A whole fuzzy system includes four components: fuzzy rule base, fuzzy inference engine, fuzzifier and defuzzifier. Figure 1 shows the fuzzy system where inputs and outputs are real-valued variables. We introduce Mamdani fuzzy inference systems as our fuzzy inference engines. Mamdani fuzzy inference systems use algebraic product base on (2) as our T-norm operators and max-product composition in (4) as our composition operators [24].

Algebraic product: T_ab (a , b) = ab                   (4)

ц !B (y) = шах^[Ц д (x)^ R ⁽x,y^)] = V,, ^[ц_А (х)|^(х,у^)]

Premise 1 (rule 1): if x ₁ is A¹ and x ₂ is A¹ then (6) у is В ¹

Premise 2 (rule2): if x 1 is A1 and x2 is A2 then у is В2

Premise 3 (fact): if x₁ is A₁ and x₂ is A ₂

Conclusion: у is В

В'= [(/1 X /2)°(/1 X /11 ^ В 1)] и [(/1 X /2)°(/1 X /2 ^ В 2)] = [(/ X /2)°R1 ] и [(/1 X /2 ) °R2] = defuzzifier, we use its approximation: the center average defuzzifier.

^В1 ^{и В} 2

Based on the two rules with two antecedents in (4), we use max-product composition for the operator and maximum operation for the U operator in (5). The membership function of fuzzy set B' is given by

. в (У)

= max² l=1 max x1,x2

I / 1 (X 1 )1 / 2 (X 2 ) ^ . / (X t ) ._Bi (у)

1=1

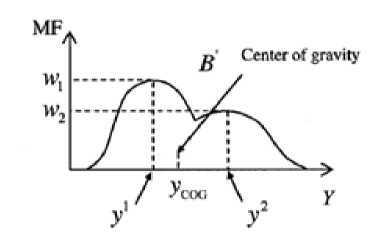
Figure2: Defuzzification of fuzzy set B'

A fuzzifier is defined as a mapping from a real-valued crisp point X * to a fuzzy set

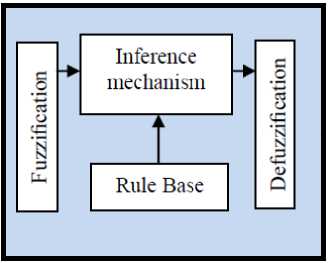
Figure 1 : Basic configuration of fuzzy systems

A_t To simplify the computation in (6), we introduce the singleton fuzzifier:

The center average deFuzzifier is defined as

52=1 у¹. в₁ ⁽у^{1) у}С0С = _y2  „ _л л n

• ⁵ l =1 . В ₁ ^{(У )}

  ⁵ l=1 У¹” 1

  ⁵ l=1 ^w l

  
  
  
  

Where у¹ and у² are the centers of В 1 and В ₂ in (5); w 1 = . B 1 (У 1 ) and w₂ = . в₂ (У²⁾ are shown in Figure 2. If all fuzzy membership functions are symmetric, we can get: у¹ and У ² are the centers of B 1 and B₂ ; w 1 and w₂ are the heights of fuzzy set В related to у¹ and y² . We derive the membership function of the fuzzy set B i at the point У¹ from (8). We can get ._{B l} (у¹ ) = .^ (X*). / (x2)ii_b i (У¹ ) . Assume the fuzzy set B^l is normal, we get ц_В1 (У¹ ) = 1 . The membership function of the fuzzy set B_l at the point у ¹ becomes ц_В, (У¹ )= .л ⁽x 1 )|Z. l (х 2 ) . Equation (10) ^{l               /} 1          ^/ 2

becomes

. / (X ) = {0

tfX i = X *⁽ t = 1,2) others

5 2=1 у¹.в₁(у¹)

^{У с/} = 5 2=1 . в₁ (У)

Since, ._/ 1 ⁽x 1 ) = ._{/ 2} (x * ) = 1 , we can reduce (6) into:

.в (У) = max21=1 [П2=1 ^i (X* ).Bi (У) ]= max2i=1 [.в1 (У)]

In (8), the output B' is a fuzzy set with the membership function . в (у) . To use a fuzzy system as a controller, we need a crisp output. We use a defuzzifier to map a fuzzy set to a single point. We introduce two defuzzifiers: center of gravity dcfuzzifier and center average defuzzifier [25-28].

The center of gravity defuzzifier is defined as

5 2=1 у¹[п2=1 . /l (x * ⁾ ] 52=1|п2=1 . /l (x * ⁾ ]

III. METHODOLOGY

A useful family of computed fuel ratio controller (CFC) is PD plus mass of air which the results when

M air 11

M¹ air 21

M air12

air22

]=^;, ⁿ =[M a1 ]• Based

on CFC

method and uncertainty in dynamic formulation, this

method is defined by the following formulation;

PFI

[ DI]

M air 11    M air 12

M air 21    M air 22

_ jy y._R (У)dy

У^С0С    i y I B (У ^)й У

M

⁽ FR_d + K_ve + K_pe) + [_Ma 1 ]

If the follows;

Lyapunov function in this method defined as

Figure (2) shows the centroid of area B'. We can get the point у_С0С on Y axis. Since the membership function I В (У) is usually irregular, the integrations in (9) are difficult to compute. Instead of the center of gravity

^M air 11    ^M air 12

M air 21    M air 22

V =

] X FR^T x F'R^ + (e^TK_pe)

and the differentiate to obtain

M v(fr^t) I • V Ml,

air 11

¹ f'r[ ^M

2 |м

air11

air21

air 21

м air 12

м air 22

М ■ air 12

м air 22

] х FR +

] ^- Kp^

This methodology has three main parts; linear PD part based on PD linear formulation, nonlinear mass of airpart to eliminate the term of mass of air and fuzzy like nonlinear equivalent part to eliminate the nonlinearity part. Based on this methodology;

г.

Based on CFC formulation and Lyapunov formulation in CFC;

-Гм М . гР 1

V = (^й "** _а"“ - ([^p  *llFRdJ +

M_{air 21} M_{air 22} mo tor 2

К** N * ²] х [PRT+[M a* ]+[M a* ])хFR =

Iaa

FR^TK_VFR                                    (17)

Therefore the skew symmetry of the first term is given by;

[PPI1 = [M, DIJ = №

air 11

air 21

[M a* ^]+^ ^^t

M air 12

Ml air 22

<(X )

(FR_d + Kve + k_pc) +

If the Lyapunov function in this method defined as follows;

V=

air 11

M air 21

2 ^S M=* Y j Ф^Т.Ф )

M air 12

M air 22

] х FR^T х PR) + (e T K p e) +

V = -FR^TK_VFR

and the differentiate to obtain

Based on above formulation this methodology has demonstrate stability in the sense of Lyapunov in bounded of error and joint velocity when V is negative.The method of computed torque control works quite well, and we can have better control than linear PD or PID control, but only if we have all necessary information about nonlinear dynamic formulation of system and the parameters of IC engine. These are very hard to have in practice. At the same time, the dynamics of the IC engine can change during the process, and that can affect the result of the control, too. In this case the result of CFC can decrease because the inquiry of dynamic model. To avoid of this situation fuzzy logic method can applied to PD plus mass of air method to estimate uncertainty and nonlinear part which it is caused to reduce the performance quality. In this case we can achieve the desired settling time and we can achieve very small steady state tracking errors. Based on fuzzy logic methodology

f(x) = u_fuzzy = Z f.* 0^T < to                     (19)

where 6^T is adjustable parameter (gain updating factor) and ^(x) is defined by

= =——                       (20)

S f ^ ^(r i )

Where /z(x,-) is membership function. T ^ _uzzy is defined as follows;

r^z, = S=* eTfW = [P”“ 1][FR6|] + motor 2

[N ** N*^ [FR]²                              (21)

VI =

(>«([M

air 11

M

M

air 21

„*,

air 11

air21

M ■ air 12

M ■ air ₂₂

M ■ air 12

M ■ air 22

х PR +

] — K p e)+ ^{s m} =* Y" ф

Based on (14) and (15);

[N **    N *2

N 21   N 22

'^T. 4> j

M air11

air 21

M ■ air 12

M ■ air22

]- ([P m^* ][FRd i l + motor 2

] х [FR]² + [M a* ]+[M a* ])xpr+

I

a2

a2

SM-i - фт. ф), = PRTKVPR + SM-i -фт. Ф

J ^Y j                ^j                                            J ^Y j                ^j

Y j

Therefore the skew symmetry of the first term is given by;

V = -FR T K v FR - 1 ]=* - ф^т. ф) j                    (26)

^Y j

IV. RESULTS AND DISCUSSION

Proposed fuzzy PD plus mass of air control (proposed) and PD plus mass of air controller (PDM) was used to decrease the error and increase the efficiency of FR method. This design was implemented in MATLAB/SIMULINK environment. Fuel ratio adjustment is used to test the stability in certain environment. Disturbance rejection test is used to test the stability and robustness in presence of uncertainty.

Adjust the fuel ratio: based on proposed formulation in PD plus mass of air method and fuzzy PD plus mass of air method; the performances of these controllers are depended on the PD ( K_p aruiK_V ) and gain updating factor

coefficients. These factors are calculated by optimization method.

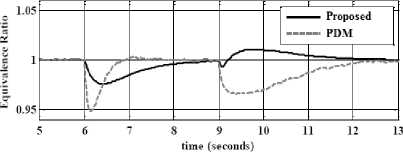
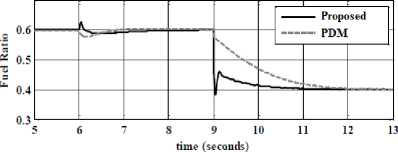
Figure3 : Fuel adjusts performance; fuzzy PD mass of air methodology and PD mass of air method

Based on simulation results the Steady State error in proposed method (Steady State error =4e-6)is fairly lower than PDG’s (Steady State error = 4e — 3 ). Based on Figure 3, this performance is used for comparisons of above methodologies in certain systems. In this state, both of these methods have acceptable result. By comparison with the PDG, proposed method ismore stable.

Disturbance rejection: Figure 4compares the result rate in the proposed method and PD plus mass of air in presence of 15% disturbance. The disturbance rejection is used to test the robustness comparisons of these two controllers for desired fuel ratio. It can be implied that the band limited white noise with predefined of 15% the power of input signal is applied to systems. It is noteworthy that the proposed method in presence of uncertainty is more stable thanPDG.

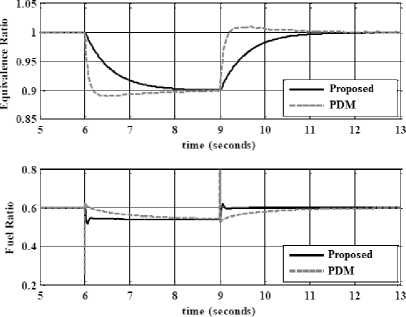
Figure4: Disturbance rejection; fuzzy PD mass of air methodology and PD mass of air method

According to the Figure 4; by comparison with PD plus mass of air method overshoot’s (9.1%), fuzzy PD mass of air method’s overshoot (1%) is more robust. response trajectory with 15% disturbance of relative to the input signal amplitude in proposed method and PDM, proposed method’s rise time (0.48) is lower thanPDM’s (0.66).

• V. CONCLUSION

This research has studied PD plus mass of air design for the dynamics of IC engine without knowledge of the boundary of the disturbances/uncertainties, using fuzzy PD plus mass of air controls as robust controls for the IC engine and as a solution to the problem of stability and robustness. To elucidate this, aPD plus mass of air control for the IC engine which includes the unknown bounded disturbances and uncertainties is studied. A PD plus mass of air is introduced as a robust control, which provides ultimate accuracy in the presence of the matched bounded disturbances/uncertainties. The result has problems because some parameters are unknown which caused to oscillation; the oscillation may actually damage components and cause loss of accuracy of output. As a solution, model reference fuzzy method is introduced. Fuzzy method mitigates oscillation by model like systems dynamic. To conclude, the fuzzy PD plus mass of air control is demonstrated to be the robust control for the unmodeled system, and an effective algorithm to avoid overestimation of controller gains and to mitigate oscillation by model reference fuzzy method.

ACKNOWLEDGMENT

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Research and Development Corporation Program of Iran under grant no. 2012-Persian Gulf-2B.