Design of a Novel Shape Signature by Farthest Point Angle for Object Recognition

Published Online December 2014 in MECS

Digitization of images lends information are implemented. Nevertheless, Information management is successfully carried out through the manipulation of digital images [1]. Detection of similar images of objects from the available digital content is a challenging task. The objects can be recognized precisely based on their visual features. However, the shape feature makes the objects accurately distinguishable. As such, shape based techniques [2] of object recognition are reported as convincing and promisive. The content of phase and its representation as the shape conceives crucial and deterministic information. As such, the processing of information in this stage is a crucial interface as to account for possible gain or loss of information during the projection of real data into a 2-D image plane. On the other hand, the object recognition reduces to be a complex process, when the input image is infected with noise, gets defected, becomes distorted or occluded. With respect to the conceivable image information, the shape based representation methods are classified in to two categories, either following contour based or content based [3] recognition of regions. The contour based representation involves the evaluation of various descriptors positioned on the contour of the object, while content based representation requires evaluation of descriptors positioned over the entire content. However, both of these representations independently adopt spatial or transform domain [4] or structural or global approaches [4] to enrich the quality.

Zhang et al [4] reviewed various techniques of shape representation and description. In content based shape representation, description of the object is carried out by their ‘moments’ as they able to reflect the geometrical aspect of object. Moment Invariants [5], Zernike Moments [6, 7], Krawtchouk moments [8], Chebyshev moments [9, 10] represent some other types of popular moments used for region based descriptors. The regional shape representation methods include the procedures viz., the medial axis transform [11, 12, 13], grid method [14], generic Fourier transform [15], convex hull [16], shock graph [17] and shape matrix [18] etc. For the case of similar objects, the recognition rate of region based methods is found to be low, when compared to that estimated contour based methods. The contour based methods involve an additional processing step, viz., contour extraction of the object. Thus, the features extracted are positioned on contour. In contrast to the region based methods, contour based methods require significant [4] less amount of information for description. The Curvature Scale Space descriptors (CSSD) and Fourier Descriptors (FD) represent the prominent contour based descriptors [19]. The corresponding characteristics of description viz., derivatives, normalization constants and the robustness of Fourier descriptors are reported to be efficient, and hence they are extensively used in applications. The Fourier transform can be applied on either 1D or 2D signals. The 2D contour of the object can be represented by the 1D shape signature. Zhang et al [19] analyzed FD and CSSD descriptors and proved that the performance of FD is superior to CSSD. Some of the recognition algorithms [20] use only as the shape signature projected through the feature vector. Bernier et al [20] represented the shape using the polar transform with distance and angle of each contour point wrt a common center. To test their robustness i.e. whether these features remain invariant to operations like translation, rotation and scaling; an additional mechanism wrt maximum distance is usually involved. Kindratenko [21] analyzed various contour functions i.e., cross section, radius vector, support, width, parametric constants or coefficients, complex, tangent angle, curvature etc. Nevertheless, these representations are compared with statistical features, moment invariants (MI), FD, CSSD, Wavelet Descriptors (WD) and Radon Transform (RT). Kunttu et al [22, 23] introduced the Multiscale FD descriptor through the complex wavelet transform involving the coefficients of WD in each scale, and found an improved FD and CSSD which however includes an additional mechanism. Chalechale et al [24] described the shape wrt the statistical distribution of edge pixels. They measured the local features with in each of the angular divisions. The feature vector is constructed by using FD. These features are testified and found invariant to scaling and rotation. But, they are found to be invariant for small translations only. Zhang et al [25] evaluated various shape signatures for 1-D FD basing on the features like centroid distance, area, affinity, position, chord length, curvature and psi etc., and concluded that centroid distance and area FDs are better measures for object recognition. However, the first ten FD coefficients are found to be sufficient for describing the most generic shape of the object. Centroid distance signature is further extended to fuzzy sets by Chanussot et al [26], where in the signature is constructed by a membership function and α-cuts. The Euclidean distance (ED) [27] is also prevalently reported for the shape toning process. The efficiency of technique by Capar et al [28] is found to be enhanced by replacing with the directional Gauss gradient filter with Centroid distance. Capar relies on active contour model for segmentation and recognition of objects. Shape histograms (shapemes) are found to be effective for shape toning and object recognition. Shan et al [29] represented the object model with bundle of shapemes where in the shape toning process involves the evaluation of the constrained projection of the test histogram. Mocanu et al [30] presented various ways of boundary based shape representations, such as FD, turning angle, centroid radii, distance histogram and centroid radii with turning angle methods. The centroid radii with turning angle method is found to improve the performance [30], while turning angle method is found to turn over poor performance. Guru et al [31] attempted to combine the contour and region information of the object during its representation and description, such that it would remain invariant to translation, rotation, scaling, although it is susceptible to occlusion and deformation operations. Conseil et al [32] has compared the FD and HU moments and found that the efficiency increases for FD by exhibiting grater robustness to real objects. Zhang et al [33, 34] found that the efficiency fits enhanced by using the Fourier transform, compared with the centroid distance shape signature and the pixel brightness parameters. The Yu et al [35] method involves the tangent angle histogram and image registry wrt the centroid and the length of the contour, and claims more effective, especially for automatic registration of images. Yadav et al [36] reported a method for vehicular shape based objects, using the centroid distance signature (for FD and ED in the shape toning phase), while the FD outperformed the WD. Ghazal et al [27] reported an enhanced utility method for the estimation of the centroid distance signature, reclassified as Farthest Point Distance (FPD). FPD method measures the distance between each contour point and the corresponding farthest corner of the object wrt the centroid. However, ED is used for shape toning process. Ghazal’s findings proved that FPD based shape signature turned out with greater retrieval performance, when compared to other methods that rely on signatures like radial signature, chord length, angular function, triangular centroid area, triangular area representation, complex coordinates, polar coordinates and other methods (Zernike Moment and CSSD) etc. Schlosser et al [37] proposed for shape context based shape signature, which is found to perform better when the point correspondences are extracted based on shape context. The histogram method proposed by Zhang et al [38] contains the length ratios and angle between centroid and the contour point to conceive both of the rectilinear and curvilinear information. Zhou et al [39] introduced the idea of shape signature through Homotopic deformation (HDBS) containing the length of each contour point to the minimum concentric circle of the shape and is found to be the most suitable for special cases of complex and concave shaped objects.

An angle based histogram method developed by Zhang et al [40] includes measurement of angle between the local maximal curvature and the centroid, where the shape toning process describes the global shape in terms of the local descriptors and their combinations. Liu et al [41] proposed a distance angle pixel measure as a feature vector containing principal angle which later found to be susceptible to geometrical invariance. Amanatiadis et al [42] estimated the performance of FD, CSSD, Angular Radial Transform Descriptor (ARTD) and Moment Invariant Descriptor (MID) and found that the MID is giving better performance, while ARTD identified with least size for the feature vector. Tiagrajah et al [43] explained the relevance for radial distance in their triangular centroid area (RDTCA) signature, later found to suffer with a drawback of poor characterization of local shape feature. To overcome this drawback, Wang [44] suggested for a perimeter area function (PAF), however the Fourier transform applied on the PAF signature and combined with the centroid distance resulted for the larger size of feature vector.

Zunic et al [45] computed the shape centredness and estimated the distance from the interior and contour points as descriptors, which involve additional mechanism of shape centredness and found to be invariant wrt translation, rotation and scaling transformations. Ghazal et al [46] combined the Fourier transform with the multiscale representation, where in the curvature scale image is constructed for each scale using the 2-D Fourier transform, which is found to involve more processing time. Eini et al [47] constructed the signature with the distance radii and the corresponding minimal rectangle for each contour point involves the feature vector constructed through the FD coefficients and is invariant to translation, scaling and rotation. Bercovich et al [48] reported the construction of shape signature with the ED between the centroid and the normalized tail head contour and found that the FD of the object signature increases the performance. Pedrosa et al [49] method which describes the shape of the object by using angular position of collection of points (i.e. elevated curvature points as salience points) measured in multi scales. The adopted similarity algorithm (with local and global features on dynamic programming for shape toning) is found to consume more time than the simple distance measure like Euclidean Distance (ED).

The shape context [50, 51, 52] is a popular method for shape based object recognition. This includes the computation of point correspondences between different points and uses an aligning transform. Shape descriptors based on the eigensystems of Laplace and LaplaceBeltrami operators are becoming popular [53, 54, 55]. These methods use spectral signatures and spectral distance methods. They are lacking with the transformation of local shape information into an overall shape dissimilarity measurement.

In the wake of the reported techniques with the characteristic merits and demerits, the FD method seems to present a superior method to various other contour based shape description methods. In general, the shape of the object can be represented either by the distance or the angle measurement. Among these, the angular measurement will capture finer details about curvature of shape. Though there are prominent shape signatures for representing the shape by angle, more efficient signature is needed to reduce the feature size, complexity (feature vector description and shape toning), processing time and improve the accuracy. Presently, the authors propose a novel method of estimation of shape signature usable for contour based shape representation techniques. The object description is carried out by the angle measurement method i.e. angle measured between the farthest corners wrt the centroid. The corresponding histogram for every 15o angle is estimated and the corresponding FPA is retained as a characteristic feature. Further, the 1-D Fourier transform is applied on FPA, while ED is used for the shape toning to enhance the quality.

The paper is organized in three sections. Introduction to the computerized object recognition method is presented in section-1 containing specific introduction to the contour based shape representation procedures. Methodology adopted for the present FPA technique is systematically presented in section-2 along with the indices involved to evaluate its performance. The results obtained by adopting present FPA technique to the stated databases and their trends are presented in section-3 along with the discussions of relative performance.

• II.    Methodology

Presently, a novel scheme for object recognition process designed to use FPA signature is proposed. The details of various stages of processing of information are presented in section-II.A, while the details of performance indicators are presented in section-II.B.

• A.    Design of System

  The standard databases [56, 57] frequently used for the evaluation of shape descriptors are identified as Kimia {K-99, K-216} and MPEG CE-1 Set B. It is noticed that the Set B database characteristically includes rotated, scaled, skewed and defected shapes. However the K-99 database is known to include the partially occluded shapes. The K-216 database represents a sub database of Set B and contains partially occluded shapes. The K-99 database consists of nine groups each group contains eleven images, with a total of 99 images in the database. The K-216 database possess eighteen groups with each group contains twelve images, with a total summation of 216 images. Set B has seventy groups with each group having twenty images making up to a sum of 1400 images. The details of various stages involved with the proposed object recognition by using FPA are schematically depicted in Fig. 1. The proposed system consists of four successive steps viz.,

• (i)    Shape representation with contour

• (ii)   FPA signature construction

• (iii)    Shape description by using Fourier Transform and

• (iv)    Shape Toning and Ranking, respectively.

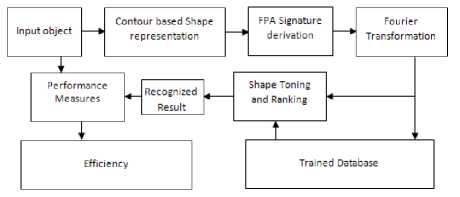
Fig. 1. Schematic diagram of the proposed system with FPA signature.

The shape based object recognition system further includes various stages such as shape representation, shape description and shape toning. Present contour based shape representation is considered as the first step. The second step includes description of the representative shape. During the shape description, an interval transform is applied on the representative shape. The 1D transforms through the Fourier Transform, while scaled space and wavelets are used as tools of description. The contour of the object is represented as 1D shape signature signal. During the representation of the shape, signature defined such that it plays a vital role during the process of shape toning [27]. Further, it entails the complete information about the 2D object. Transition points and corner points are included in the shape signature in anticipation of an effective retrieval performance. In the following stage, shape signature is compared with Farthest Point Distance (FPD) as reported by Ghazal [27] and several other methods. The construction of FPD signature is represented in Fig. 2(a). The FPD signature corresponding to the object which includes the Euclidean Distance (ED) from center of the object to extreme corners is given by (1);

FPD ( x , y ) = ED { ( x , y ), ⁽ x c , У с ^{) }} + ED ^{{ (} f, , f y ), ⁽ x c , У с ^)}     (^

where,

ED{(x,y),(xc,yc)} represents the ED between the contour point and the centroid and

ED {(f, f ),(x , y )} represents the ED between the farthest contour point and the centroid.

A new shape signature called as Farthest Point Angle (FPA) is evaluated which measures the angle between the line from the contour point and the line from the farthest corner point. The construction of FPA signature is achieved through (2);

FPA ( x , y ) = Tan - 1 f m ^{2 -} m ¹  )

^ 1 + m , x m ₂ J                 (2)

where,

M1 is the slope of the line from the contour point to the centroid and

M2 is the slope of the line from the corresponding farthest point to the centroid.

The FPA signature is defined as picturized in Fig. 2(b). The FPA for each of the contour point and the corresponding farthest point is evaluated and the corresponding histogram for every 15o angle is generated.

During the second step of processing, the characteristic FPA signature is constructed. During the third step, the feature description of the shape of the object is addressed.

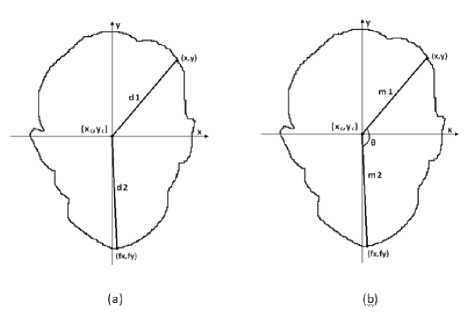
Fig. 2. Shape signature for a contour point wrt the corresponding farthest point.

In shape based object recognition technique, Fourier transforms are widely used for description [46]. Hence, Fourier transform is applied on the proposed FPA signature to describe the feature vector of large size, which contains a good number of coefficients. The lower order coefficients contain essential, vital and important information of shape of object, the higher order coefficients contain little information. So, for this case of shape based object indexing, only first few coefficients are considered to generate the feature vector. Thus, a significant reduction in feature vector size is designed in the present FPA technique. The size of the shape representation points is an important and influential factor that optimizes the effective usage of Fourier transformation. Hence, in the shape signature generation process, the sampling is considered as a mandatory step. Equal Point (EP), Equal Angle (EA) and Equal Arc Length (EAL) [19] are the methods presently considered for such sampling. EAL is expected to yield for a better equal space [58] than the other two methods. By using EAL, the representation of the contour is restricted to N-number of points. The proposed FPA signature uses EAL method to sample the finite number of contour points. For a given contour signal, the 1-D Fourier transform is given as;

N -1           f " j^{2 n nt} )

FD„ = — E s ( t ) x e ^ N >           ⁽³⁾

" Nt=o where,

S (t) represents the 1-D contour signal and N represents number of representative points of the contour.

Using (3), the required Fourier Descriptors of size ‘N’ are generated. Further, the extracted features are testified as invariant to translation, rotation and scaling operations performed over the set of images. In the wake of the fact that the FPA signature is obtained wrt centroid, the obtained features are found invariant to translation. The resulting finite and stipulated magnitude values of the features, the rotation invariance is validated. For the present method, the scaling invariance is achieved by dividing the features with the first feature value. In the third step, the feature vector is constructed, which describes the entire shape features of the object. To further improve the quality of FPA signature, three global descriptors (GD) are augmented to the FPA signature feature vector. The GD feature vector {S,C,A} contains the measures of solidity, circularity and aspect ratio. In the fourth step, the shape toning process is executed. The distance with ED is estimated as given by the (4) in order to test and expose to the process of shape training (i.e. during the identical shape toning process).

ED(TE , TR ) =   2 ( TE. - TR )²

V i =1                                  (4)

where,

TE represents the test shape feature vector,

TR represents the trained shape feature vector and

M represents the length of the feature vector.

Inclusion of GD is effectively carried out through the computation of relative distance using the following (5) and (6) given by:

D _X ( TE , TR )

D ( IE , TR ) = ED ( IE , TR ) +----

X^TE - X^TR

^D x (TE , TR ) = 2

max( X ^TR )

where,

ED (TE, TR) represents the ED between the test and trained shapes,

D X (TE, TR) represents the Global distance between the test and trained shapes,

X represents the GD vector {S, C, AR},

X ^TE represents the GD feature of the test shape and

X ^TR represents the GD feature of the trained shape.

The specified data of distance measurement, the distances are further rearranged in ascending order and are assigned with ranks. In turn, the system is enabled to recognize top ranked images.

• B.    Performance

The performance of various object recognition schemes reported so far employ different measures [27]. Among them, precision and recall are considered as important measures, while they quantify the similarity measurement. Precision (P) and Recall (R) are defined by;

where,

X denotes the true recognition results,

Y denotes the total recognized result and

Groupsize denotes the maximum true recognition result.

The Average Precision value for each recall is computed. This value is affirmatively grouped as two categories viz., Low Recall (LR), High Recall (HR). The Average Precision for Low Recall (APLR) denotes the average precision for recalls less than equal to 50. In contrast, the Average Precision for High Recall (APHR) represents the average precision for recalls greater than 50. The False Detection Rate (FDR) for each image is calculated by:

FDR = z/              (9)

y where,

Z denotes the false recognition result and

Y denotes the total recognized result.

The average FDR (AFDR) value of all test images corresponding to each database is calculated. Apart from the usual recognition rate, the Average Processing Time (APT) is also estimated for each query in the shape toning stage. The proposed FPA+GD signature is compared with four standard descriptors viz., Angular Radial Transform Descriptor (ARTD) [33], Moment Invariant Descriptor (MID) [33], Zernike Moment Descriptor (ZMD) [43] and Curvature-Scale-Space-Descriptor (CSSD) [43].

The performance for the present FPA technique is evaluated in the wake of reports from Amanatiadis et al [42] and Ghazal et al [27] with the Feature size of 35 for ARTD (n<3, m<12), 6 for MID, 34 for ZMD (order from 2 to 10). Hence, the same feature vector sizes for ARTD, MID, ZMD are used to estimate the performance. But, the CSSD feature size is varied from one image to another because of variation in no. of in the peaks. Nevertheless, the evaluation of all the described metrics are used to estimate the performance viz., APLR, APHR, AFDR and APT for the proposed FPA signature (with inclusion of GD), FPD signature (with the inclusion of GD), ARTD, MID, ZMD and CSSD.

• III.    Esults And Discussion

The present FPA based object recognition method is estimated as detailed in section-2.1 corresponding to the input of standard databases that yielded the following results at various steps of processing. The results obtained in various steps and their trends are presented in the following sub section-III.A. The performance of the proposed FPA method is also analyzed in the ongoing sub section-III.B.

• A.    Processing of FPA based Object Recognition

Presently, the shape of the object is processed by using the angular distance between each of the contour point and the corresponding farthest point. For each contour point the angle is measured (i.e. wrt the corresponding farthest point and centroid) within the range of 0o to 360o angle viz., in one full rotation. A histogram is generated for every 15o angle. The FPA signatures, thus constructed are presented in Fig. 3 to 6 corresponding to four different image groups of camel, chicken, device9 and fly accessed from set B database. Fig. 3(a1), Fig. 3(b1) and Fig. 3(c1) contains three original images of camel group (camel-8, camel-14 and camel-17), the Fig. 4(a1), Fig. 4(b1) and Fig. 4(c1) shows three original images of chicken group (chicken2, chicken3, chicken16), the Fig. 5(a1), Fig. 5(b1) and Fig. 5(c1) gives three original images of Device9 group (Device9-9, Device9-15 and Device9-18) and Fig. 6(a1), Fig. 6(b1) and Fig. 6(c1) contains three original images of Fly group (Fly11, Fly12 and Fly13). The corresponding images contour is given in Fig. 3(a2) to 6(a2), Fig. 3(b2) to 6(b2) and Fig. 3(c2) to 6(c2). The constructed FPA is shown in Fig. 3(a3) to 6(a3), Fig. 3(b3) to 6(b3) and Fig. 3(c3) to 6(c3). It is clearly noticeable that from Fig. 3 to 6 that the FPA signature is found to be same for the different shapes within the same group while it assures difference from one group to another. Basing on 1-D shape signature signal, the Fourier descriptors are generated, where in the first ten features are used to design the feature vector [25]. In the present case, the FPD signature presents feature vector size of 63. First ten FD coefficients for Device9 and Fly images are presented in Table 1. From Table 1, it is found that the FDs of each group of images possess similar value, although they differ regarding there of group identification.

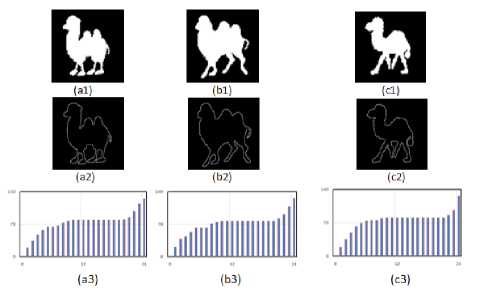
Fig. 3. FPA signatures for three Camel group Images.

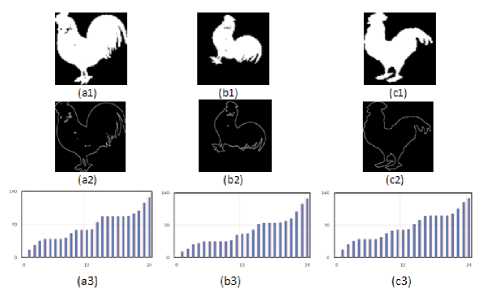
Fig. 4. FPA signatures for three Chicken group Images.

Table 1. First ten FD coefficients of three images of Device9 and Fly Groups.

	FD,	FD;	FD,	FD:	FD;	FD:	FD,	FD:	FD,	FD,	Avg.
deviceM	0.048	0.047	0.015	0.025	0.01!	0.001	0.012	0.020	0.027	0.033	0.026
deviceMS	0.044	0KB5	0.013	0.024	0.014	0.003	0.007	0.017	0.025	0.031	0.024
deviceMS	0.055	0.051	0.011	0.031	0.017	O.M	0 008	0.018	0.029	0.034	0.029
Flyll	0.041	0.020	0.030	0.062	0.056	0.046	0.045	0.044	0.045	0.048	0.044
Hyl2	0.06?	0.021	0.002	0.039	0.036	0.044	0.039	0.045	0.046	0.047	0.039
Flyli	OJE	0.038	0.025	0.005	0.021	0.036	0.044	0.049	0.053	0.055	0.040

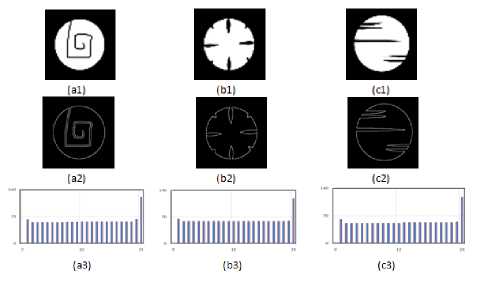
Fig. 5. FPA signatures for three Device9 group Images.

In the present object recognition process, ED measure is also computed between the target and test objects and concurrently they are allocated with ranking according to their distance. The top n-ranked objects are used to estimate the precision and recall parameters, where ‘n’ notifies to the group size of {Set B: 20, K-99:11 and K-216:12} sets. For each database, the accuracy for the retrieval results corresponding to top ‘n’ (group size of the corresponding database) number of images is illustrated in Fig. 7 to 9.

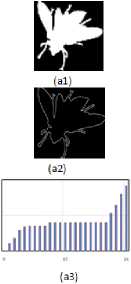
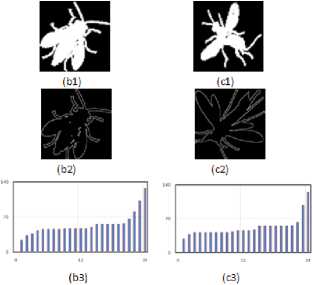
Fig. 6. FPA signatures for three Fly group Images.

For the K-216 database, the top 12 ranked images for the query image i.e. for Bone5 by using FPD+GD and FPA+GD projected in the Fig. 7. The Bone5 query image is shown in Fig. 7(a) while Fig. 7(b) illustrates the retrieval results with FPD+GD signature, Fig. 7(c) portrays the retrieval results with FPA+GD signature. In case of K-99 database, the top 11 ranked images corresponds to the query image Fish4 by using FPD+GD and FPA+GD are generated and presented in the Fig. 8. The Fig. 8(a) gives the Fish4 query image, Fig. 8(b) gives the retrieval results with FPD+GD signature and Fig. 8(c) gives the retrieval results with FPA+GD signature. For the set B database, the top 20 ranked images for the query image Glass11 by using FPD+GD and FPA+GD are presented in the Fig. 9. The query image Glass11 is illustrated in Fig. 9(a), the retrieval results with FPD+GD signature are illustrated in Fig. 9(b) and the retrieval results with FPA+GD signature are illustrated in Fig. 9(c). Overview of Fig. 7 to 9 suggest that, the FPA+GD signature is preferable to retrieve more relevant images with strong correspondence than that retrieved with the FPD+GD method.

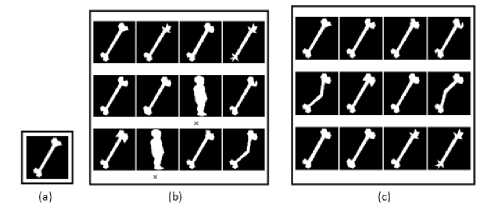
Fig. 7. Retrieval results of Bone 5 test image from K-216 database.

Fig. 8. Retrieval results of Fish 4 test image from K-99 database.

(a)

(b)

h^Md ЬШЙЙ ЙНЙ>< Uhh^ ^GK2

databases are estimated by the relevant formulae as detailed in section-2.2. The FPA signature is found to give improved results than that with the FPD signature. Hence, the FPA signature is confirmed to enhance the quality of APLR values in comparison with the APHR. It is also noticed that FPA is accompanied with improved results and with reduced size of feature vector, viz., by 10, in contrast with the FPD signature where in the size is 63. An overview of the results over all the three databases, it is uniquely found that better results are obtained by using FPA signature. Hence, the inclusion of GD during the processing is also considered for the estimation of FPD and FPA signatures for all the three databases {Set B, K-99 and K-216}. The corresponding yield of results is presented in Tables 2 to 4. This GD inclusion procedure is found to increase the values of APLR and APHR of FPD and FPA signature {FPD+GD, FPA+GD}. The result in Tables 2 to 4 clearly speaks out that the FPA+GD signature is enhancing the FPD+GD signature for all the three databases under consideration. It is observed that in both of the FPD+GD and FPA+GD signatures, the feature vector size is taken as 13. However, the procedure is carried out by varying the size of the GD feature vector also. The variation of GD {S, C, A} vector is found to result for improved results than the other methods, which use combinational feature vectors.

Table 3. The APLR and APHR values for FPD, FPA, FPD+GD, FPA+GD signatures with K-99 database.

Signature	APLR	APHR	Average
FPD	80.69	44.00	62.35
FPA	83.34	45.84	64.59
FPD+GD	85.64	50.70	68.17
FPA+GD	89.26	60.32	74.79

Table 4. The APLR and APHR values for FPD, FPA, FPD+GD, FPA+GD signatures with K-216 database.

Signature	APLR	APHR	Average
FPD	79.50	44.06	61.78
FPA	84.92	49.90	67.41
FPD+GD	83.81	50.52	67.16
FPA+GD	89.91	62.64	76.28

Table 2. The APLR and APHR values for FPD, FPA, FPD+GD, FPA+GD signatures with Set B database.

Signature	APLR	APHR	Average
FPD	75.82	42.13	58.98
FPA	76.05	42.45	59.25
FPD+GD	82.42	50.62	66.52
FPA+GD	82.51	50.94	66.73

Fig. 9. Retrieval results of Glass 11 test Image from Set B database.

• B.    Performance Evaluation

The APLR and APHR values of the present FPA signature based object recognition technique for different

The average precision for each recall is estimated (section-2.2) and plotted by the Precision-Recall (PR) plots. The PR plots of four signatures {FPD, FPA, FPD+GD, FPA+GD} for the three databases are illustrated in Fig. 10 to 12. Fig. 10 stands a representative PR plot for Set B database. The results from the Fig. 10

are grouped into two categories {FPD and FPA} and {FPD+GD and FPA+GD}, where within each group, the two signatures are successfully yield for comparable precision measure for each recall. However, between two groups, an increase in the precision measure is observed. The second category (inclusion of GD) increases the precision result at both low recalls i.e. at 10 to 30 and high recalls i.e. at 60 to 90. At some other specific recalls i.e. at 40, 95, 100, the result of FPA+GD signature is having increased value, where the remaining signatures are having almost similar value. The PR plot for K-99 database is presented in Fig. 11. It is clear that, at each recall, FPA signature is found to attain improved performance measure than FPD signature, FPD+GD signature is found to achieve improved performance result than FPA signature and FPA+GD signature has gained improved performance result than the FPD+GD signature result. The FPA+GD signature is found to be improved through the precision measure of FPD+GD signature at high precision recalls i.e. at 60 to 90. The Fig. 12 gives the PR plot of K-216 database. The result indicates that the precision measure of FPA signature is close to that of the FPD+GD signature. The FPA+GD signature is obtaining the improved precision results for each recall where the maximum improvement is obtained at high recalls i.e. at 50 to 100.

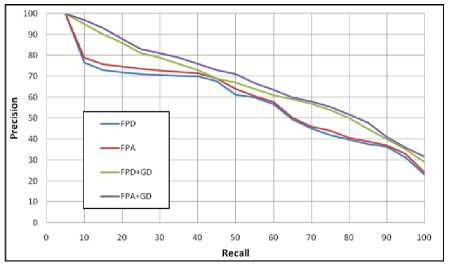
Fig. 10. The PR graph for FPD, FPA, FPD+GD and FPA+GD signatures with Set B database.

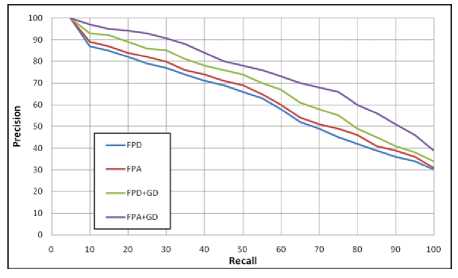
Fig. 11. The PR graph for FPD, FPA, FPD+GD and FPA+GD signatures with K-99 database.

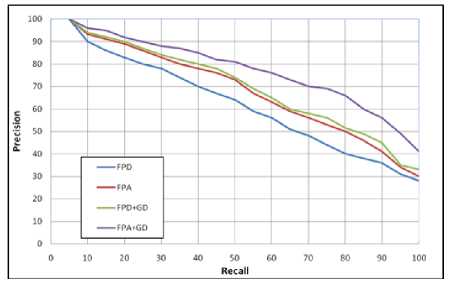
Fig. 12. The PR graph for FPD, FPA, FPD+GD and FPA+GD signatures with K-216 database.

The efficiency of the present FPA+GD signature is compared with the four standard descriptors viz., ARTD, MID, ZMD and CSSD. The yield of APLR and APHR values of our FPA+GD signature and the other four standard descriptors are explored for a comparison with three databases as presented in Tables 5 to 7. From these results, it is clearly evident that the proposed FPA+GD descriptor out performs regarding these descriptors for all the three databases. However, among the presently considered descriptors, the CSSD descriptor is found to give low performance, followed by the MID and ARTD which on the other side result for the next highest performance. But, the ZMD is found to yield improved results for K-99, when compared with the proposed FPA+GD descriptor. For the remaining two databases, the proposed FPA+GD is found to give improved results than the ZMD.

Table 5. The APLR and APHR values for FPA+GD, ARTD, MID, ZMD and CSSD descriptors with Set B database.

Descriptor	APLR	APHR	Average
FPA+GD	82.51	50.94	66.73
ARTD	82.10	45.69	63.90
MID	79.54	44.50	62.02
ZMD	82.56	45.62	64.09
CSSD	78.61	41.81	60.21

Table 6. The APLR and APHR values for FPA+GD, ARTD, MID, ZMD and CSSD descriptors with K-99 database.

Descriptor	APLR	APHR	Average
FPA+GD	89.26	60.32	74.79
ARTD	84.26	45.72	64.99
MID	81.96	44.74	63.35
ZMD	89.61	61.37	75.49
CSSD	82.32	44.11	63.22

Table 7. The APLR and APHR values for FPA+GD, ARTD, MID, ZMD and CSSD descriptors with K-216 database.

Descriptor	APLR	APHR	Average
FPA+GD	89.91	62.64	76.28
ARTD	81.35	44.67	63.01
MID	80.14	46.04	63.09
ZMD	88.94	61.71	75.33
CSSD	80.12	44.97	62.55

The PR plots for these five descriptors with set B are presented in Fig. 13; for K-99 in Fig. 14 and for K-216 in Fig. 15. The Fig. 13 reveals that all the five descriptors are yielding little enhancements to the precision measure on the Set B database. Among them, the FPA+GD is getting the improved results at higher recalls i.e. at 60 to 90. The Fig. 14 gives the PR plot for K-99 database. The precision results of MID and CSSD descriptors are nearer, where the ARTD is improving the result at high recalls i.e. at 60 to 90. The ZMD and FPA+GD are improving the precision measure at each recall. The result of Fig. 15 shows the PR plot for K-216 database. The ARTD, MID and CSSD are giving closer precision measures at each recall. The ZMD and FPA+GD are improving the precision result at each recall than the three descriptors. At high recalls i.e. at 70 to 100, the FPA+GD descriptor is increasing the precision value than ZMD. From these figures, it is clear that the proposed FPA+GD performs superior to other methods. The other Performance measures viz., Average False Discovery Rate (AFDR) and Average Processing Time (APT) are also computed as detailed in section-2.2. The AFDR estimated for the three databases is presented in Table 8. From this table, it is observed that the FPA+GD signature is giving low value for all the three databases. The APT measure is also required for shape toning stage for each of the shape descriptor. The APT is estimated for all the three databases and is presented in Table 9. The proposed FPA+GD descriptor is having less APT value when compared with other descriptors. Hence, the results providing high efficiency as noticed through the proposed FPA+GD signature.

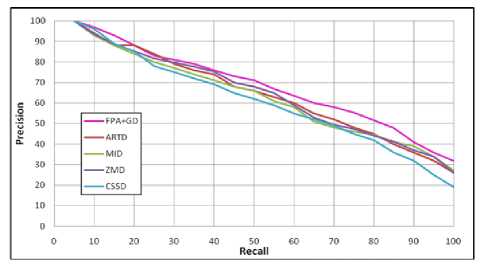
Fig. 13. PR graphs of FPA+GD, ARTD, MID, ZMD and CSSD with set B database.

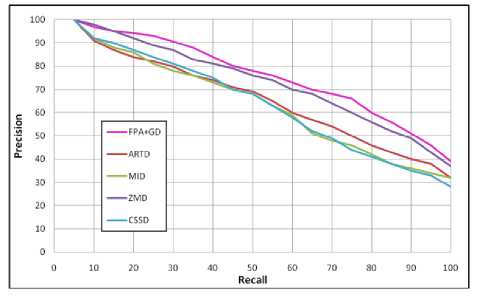
Fig. 14. PR graphs of FPA+GD, ARTD, MID, ZMD and CSSD with K-99 database.

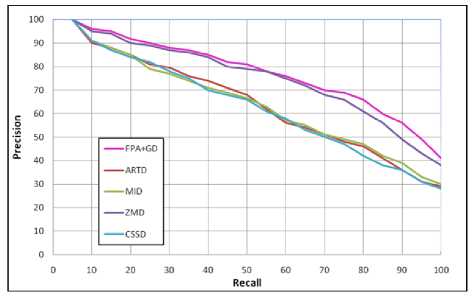
Fig. 15. PR graphs of FPA+GD, ARTD, MID, ZMD and CSSD with K-216 database.

Table 8. The AFDR for FPD, FPA, FPD+GD, FPA+GD signatures with three databases.

Descriptor	AFDR
	Set B	K-99	K-216
FPA+GD	0.74	0.75	0.76
FPD+GD	0.75	0.78	0.79
ARTD	0.90	0.85	0.86
MID	0.91	0.81	0.84
ZMD	0.78	0.76	0.76
CSSD	0.84	0.88	0.89

Table 9. APT of FPA+GD, FPD+GD, ARTD, MID, ZMD and CSSD descriptors with set B database.

Descriptor	APT
FPA+GD	0.0011
FPD+GD	0.0014
ARTD	0.0017
MID	0.0302
ZMD	0.0017
CSSD	2.1640

• C.    Conclusion

• •    Inclusion of angular variables in computerized object recognition techniques like FPA enhances the performance.

• •    Consideration of FPA+GD signature performs better than of the FPD signature.

• •    Standard measures viz., APLR, APHR, AFDR and APT can be used as performance metrics for a PC based system of object recognition through angular measurements.

• •    Inclusion of descriptors like APLR, APHR, AFDR and APT leads to the reduction of space occupancy.