Design of a Robust, Computation-Efficient and Secure 3P-EKE Protocol using Analogous Message Transmission

Published Online May 2016 in MECS DOI: 10.5815/ijcnis.2016.05.02

In order to facilitate the communication over internet cryptographic algorithms are needed to establish communication in a highly secure way. These algorithms need a secret key to perform encryption and decryption.

• •    Mutual Authentication: This requirement enables the users to authenticate each other mutually. (through their identity).

• •    Resistance to password guessing attacks proposed by Ding & Hoster (D&H) [2].

• •    Session Key (SK) security : This enables that session key cannot be obtained without persistent secrets.

• •    Resistant to Trivial Attack : This ensures that one cannot compute the SK directly.

• •    Resistant to Pre - play Attack: This requirement ensures that playing on simulated system should not succeed in practice on original system.

• •    Resistant to Replay Attack : This ensures that an intruder should not succeed in replaying with the intercepted & stored messages.

• •    Resistant to  Man-in-the-middle  Attack :  By

interrupting the message, an intruder establishes his own communication with either party. This requirement ensures that the proposed protocol should be resistant to such type of attack.

• •    Server spoofing security:   If server is

compromised, it should not affect the existing protocol.

• •    Perfect forward secrecy: This requirement ensures that compromise of preserved long-life keys should not lead to the compromise of previous session keys.

• •    Known-Key Security: This requirement ensures that the compromise of one session key should not lead to the compromise of later session keys.

This paper is an attempt to propose a novel method for computing the session key based on XOR operations with analogous (parallel) message transmission which satisfies the above security requirements. The following sections provide a detailed summary of the procedures followed to design a novel protocol which facilitates a robust, secure and computationally efficient way of communication over internet.

• II.    Related Work

  Bellovin and Merrit (1992) have proved that passwordbased authenticated protocols are secure against password guessing attacks [3]. Later, various authors have proposed many two-party password authenticated key exchange (2PAKE) protocols. Due to shortfalls, 2PAKE protocols are found only suitable for client-server architecture, which motivates research community to encompass 2PAKE protocols into 3PAKE schemes for three-party communication environment.

Chang et al. (2004) [4] proposed an efficient three-party encrypted key exchange protocol (ECC-3PEKE) with both round and computation efficiencies. However, unfortunately, an undetectable online password guessing attack has been notified on ECC-3PEKE protocol by Yoon et al. (2008) [5]. At the same time they have also proposed an improvement over ECC-3PEKE protocol and claimed that the proposed protocol defends against undetectable online dictionary attacks. Also in the same year Chung et al. (2008) [6] has shown three weaknesses in a simple three-party key exchange protocol. Later, Padmavathy et al. (2009) [7] have proposed some improvement over the ECC-3PEKE protocol and claimed that the proposed protocol (PSRJ Protocol) is secure against undetectable online dictionary attacks and also achieves better performance, which requires only 4 message transmission rounds. Later, Chang et.al (2009) [8] specified the insecurity of Yoon-Yoo’s Protocol and R. Padmavathy (2010) [9] has notified an undetectable online dictionary attack on PSRJ protocol. Additionally, to overcome an attack, she proposed an enhancement over the existing protocol with reduced modular exponentiation operations. In connection with this, Shirisha Tallapally (2010) [10] has proposed an impersonation attack on ECC-3PEKE protocol. Later, Archana et al. (2012) [11] has cryptanalyzed the PSRJ protocol which forms a basis for this paper. In the same year, Raj et al. [12] proposed Security Enhancement for 3-PEKE protocol using parallel Message transmission. Later, Raj et al. (2013) [13] has discussed the performance analysis of 3P-EKE protocol using parallel message transmission technique. But unfortunately, Archana et.al (2013) [14] have notified the weakness of 3P-EKE Protocol proposed by Raj et.al (2013).

The list of notations and their descriptions used throughout this paper are illustrated in Table 1. The protocols discussed in this paper assume that the passwords Pwda (Alice) and Pwdb (Bob) should initially be shared with trusted party through a secured channel.

Table 1. List of Notations

Al ice.'Bob	Two parties who want to communicate with each other
Carol	An Attacker
Trusted Party	Trusted thir d party(Server)
Idai Idb -Id,	Identities of Alice, Bob and Trusted Party
Pwda. Pwdb	Passwords secretly shared by Alice and Bob with Trusted Party respectively
Kt	Trusted Party’s Public key
EpwdO	A symmetric Encryption scheme with a password pwd
DpwdO	A symmetric Decryption scheme with a password pwd
P	A large prime number
g	A generator in GF(Group Field)
Га,ГЬ	Random numbers chosen by Alice & Bob respectively.
REa.REb .REt	Random Exponents of Alice. Bob and Trusted party respectively
Ma Мъ	Ma=g1Ltamod p , Mb=g±U^Dmod p
Kat. Kb,	Kat=Maraniod p, Kb,—MaTOmod p are one time strong keys shared by Alice & Bob with Trusted Party respectively
ь»	A one-way trapdoor function . where only trusted party knows the trapdoor
ДО	A pseudo random hash function indexed by a key к
sk	Session Key

• III.    Analysis Of Psrj And Raj Et Al. 3p-Eke Protocols

The aforementioned sections have reviewed and highlighted the PSRJ and Raj et al. 3P-EKE protocols and its weaknesses in detail.

• A.    Analysis of PSRJ Protocol

As required, the PSRJ protocol has been reviewed and then cryptanalyzed by showing its vulnerability to online detectable dictionary attacks.

Review

In this section, we review the PSRJ protocol. The details of the protocol can be described as follows:

Step 1: Alice computes M a =g ^REa mod p & K at =M a ^ra mod p by generating the random numbers, RE a , r a Є R Z p and sends the credentials {Id a , Id b , Id t , E pwda (M a ),h t (r a ), f_Kat(M_a)} to Trusted Party.

• i.e., Alice ^ Trusted Party: {Id a , Id b , Id_t, E_pwda(M_a), h t (r a ), f Kat (M a )}

Similarly, Bob computes M_b=g ^REb mod p & K bt =M b ^rb mod p by generating the random numbers, RE b , r b Є R Z p and sends the credentials {Id a , Id b , Id t , E pwdb (M b ),h t (r b ), f Kbt (M b )} to Trusted Party.

• i.e., Bob ^ Trusted Party: {Id a , Id b , Id_t, E_pwdb(M_b), h t (r b ), f Kbt (M b )}

Step 2: After receiving the credentials from Alice & Bob, Trusted Party verifies the credentials. Then Trusted Party generates a random exponent, RE_t Є_R Z_p to compute M_b ^REt mod p & M_a ^REt mod p and sends the credentials {M b ^REt mod p, f Kat (Id a , Id b , K at , M b ^REt )} to Alice and {M a ^REt mod p, f Kbt (Id a , Id b , K bt , M a ^REt )} to Bob.

• i.e., Trusted Party ^ Alice : { M_b ^REt mod p, f_Kat (Id a , Id b , K at , M b ^REt )} and

Trusted Party ^ Bob : {M_a ^REt mod p, f_Kbt(Id_a, Id b , K_bt, _{M a} REt_)}

Step 3: Alice computes the session key SK=( M_b ^REt ) ^REa mod p and sends f_SK(Id_a, SK) to Bob.

i.e., Alice ^ Bob : f_SK(Id_a, SK)

Step 4: Bob computes the session key SK=( M_a ^REt ) ^REb mod p and sends f SK (Id b , SK) to Alice.

i.e., Bob ^ Alice : f_SK(Id_b, SK).

After Alice and Bob successfully examine the validation of the incoming messages f SK (Id b , SK) and f SK (Id_a, SK), both of them can ensure that they actually share the secret session key SK=( M_b ^REt ) ^REa (mod p)= ( M_a ^REt ) ^REb (mod p) at present. If validation fails, the protocol will be terminated. Fig 1 illustrates 3P-EKE PSRJ Protocol.

Attack

This section endeavors to demonstrate the detectable online password guessing attack on PSRJ 3P-EKE protocol.

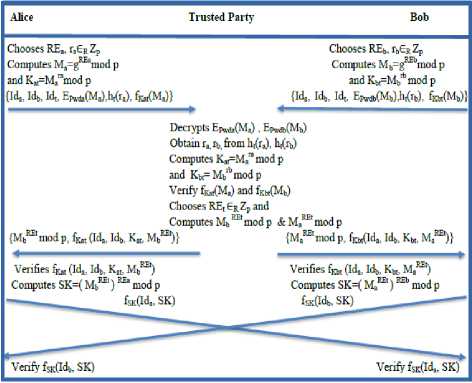
Fig.1. PSRJ 3P-EKE Protocol

The details of attack are shown below.

Step 1: User Alice generates two random numbers viz., RE a , r a Є R Z p , and calculates M a =g ^REa mod p & K at =M a ^ra mod p to compute E pwda (M a ), h t (r a ) & f Kat (M a ) and sends {(Id a , Id b , Id t , E pwda (M a ),h t (r a ), f Kat (M a ))} to Trusted Party.

• i.e., Alice ^ Trusted Party: {(Id a , Id b , Id_t, E_pwda(M_a), h t (r a ), f Kat (M a ))}.

Step 2: An invader Carol guesses Alice’s password as Pwd_a’ by intercepting the message i.e.{(Id_a, Id_b, Id_t, E_pwda(M_a),h_t(r_a), f_Kat(M_a))} and decrypts E pwda’ (M a ) & to get M a’ . Now attacker computes K at’ =M a’ ^rc’ mod p by generating her random number r c’ and sends {Id a , Id b , Id t , E pwda (M a ), h t (r c ’ ), f Kat’ (M a’ )} to Trusted Party.

• i.e., Carol sends Trusted Party: {Id a , Id b , Id t , E pwda (M a ), h t (r c ’ ), f Kat’ (M a’ )}

Step 3: The Trusted Party decrypts E_pwda(M_a) to get M_a and retrieves r_c’ from h_t(r_{c ’}) by using trapdoor[15], after receiving the credentials {Id a , Id b , Id t , E pwda (M a ), h t (r c’ ), f_Kat’(M_a’)} from the attacker Carol. Now Trusted Party computes K_at’=M_a’ ^rc’ mod p to authenticate the received f Kat’ (M a’ ). If both f Kat (M a ) and f Kat’ (M a’ ) are equal then the guessed password by Carol is correct and Trusted Party will continue with the remaining procedure of the protocol by assuming that he is in a secured zone.

If both f Kat (M a ) and f_Kat’(M_a’) are not equal, it means that the attack is detected by Trusted Party and Trusted Party terminates this protocol at current session. An intruder never sits indolent. After some time Carol repeats the same process. She will continue the same process until she hits with the successful password.

In this way a malevolent user can copycat the actual user by getting the secrete session key successfully. Fig 2 shows the detectable on-line password guessing attack.

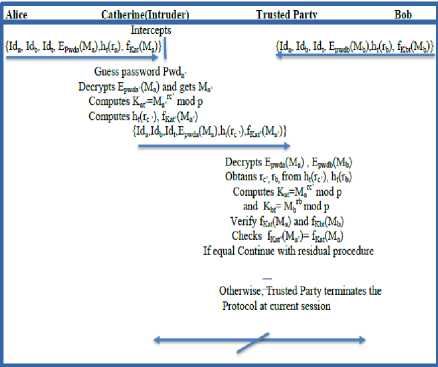
Fig.2. Detectable Online Password Guessing Attack on PSRJ 3P-EKE Protocol

• B.    Analysis of Raj et al. Protocol

This section devotes to review the Raj et al. protocol and then cryptanalyze the protocol by showing the detectable online dictionary attack.

Review

The detailed explanation is given below:

Step 1: Alice generates two random numbers viz., r_a, RE_a Є_R Z_p and computes M_a=g ^REa (mod p) & K at =M a ^ra (mod p). Then she calculates E pwda (K at ⊕ Ma), h t (M a ⊕ Id a ) & f Kat (M a ) and sends these credentials To Trusted Party.

• i .e., Alice ^ Trusted Party : {Id_a , Id_b , Id_t , E_pwda(K_at ® M_a), h t (M a ⊕ Id a ),f Kat (M a )}

Simultaneously, Bob generates two random numbers viz., r_b, RE_b Є_R Z_p to compute M_b=g ^REb (mod p) & K_at=M_a ^ra (mod p) and then calculates E_pwdb(K_bt ⊕ M_b), h_t(M_b ⊕ Id_b) & f_Kat(M_b) and sends these credentials To Trusted Party.

Here users Alice and Bob communicate with the Trusted Party in a parallel way.

• i .e., Bob ^ Trusted Party : {Id a, Id b, Id_t , E_pwdb(K_bt ® M_b), h t (M b ⊕ Id b ),f Kbt (M b )}

Step 2: After receiving the messages sent from users Alice and Bob, Trusted Party utilizes a trapdoor to obtain M a ⊕ Id a & M b ⊕ Id b from h t (M a ⊕ Id a ) & h t (M b ⊕ Id b ) and retrieves M a =(M a ⊕ Id a ) ⊕ Id a & M b =(M b ⊕ Id b ) ⊕ Id b respectively.

Next, it gets K at ⊕ M a & K bt ⊕ M b by decrypting E pwda (K at ⊕ M a ) & E pwdb (K bt ⊕ M b ) with the passwords

Finally, Trusted Party sends{M b ^REt , ,f Kat (Id a, Id b, K at, M b ^REt )} to Alice and {M a ^REt , ,f Kbt (Id a, Id b, K bt, M a ^REt )} to Bob simultaneously. If computed value f Kat (M a ) (or f Kbt (M b )) and received value f Kat (M a ) (or f Kbt (M b ))) are not identical then Trusted Party terminates the protocol.

• i .e., Trusted Party ^ Alice : {M_b ^REt , f_Kal(Id_a Id b K_at M b ^REt )},

Trusted Party ^ Bob : MR^Et , Ы^, Id b, K bt, M aREt )}

Step 3: Bob verifies the credentials f Kbt (Id a, Id b, K bt, M a ^REt ) to authenticate, after receiving the transmitted messages sent from Trusted Party. If this verification is passed, Bob believes the received M_a ^REt is valid and then computes the session key SK=( M_a ^REt ) ^REb (mod p) and sends f_SK(Id_b,SK) to Alice. Otherwise, Bob terminates the protocol.

i.e., Bob ^ Alice : f_SK(Id_b, SK).

Step 4: Similarly, Alice verifies f Kat (Id a, Id b, K at, M b ^REt ) to authenticate, after receiving the transmitted messages sent from Trusted Party. If this verification is passed, Alice believes the received M_b ^REt is valid and then computes the session key SK=(M_b ^REt ) ^REa (mod p) and sends f SK (Id a ,SK) to Bob. And also f SK (Id b , SK) will be used by the user Alice to verify the authenticity of user Bob. If this verification does not hold, Alice terminates the protocol.

i.e., Alice ^ Bob : f_SK(Id_a, SK).

Step 5: After the verification of incoming messages f_SK(Id_b, SK) & f_SK(Id_a, SK) from the other side, both Alice and Bob ensures that they actually shares the secret session key SK= ( M b ^REt ) ^REa (mod p)= ( M a ^REt ) ^REb (mod p).

Otherwise, the protocol will be terminated. Fig 3 illustrates the Raj et al. 3P-EKE Protocol.

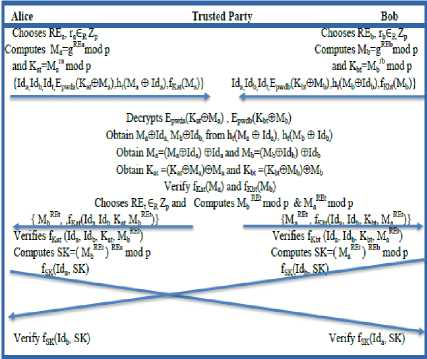
Fig.3. Raj et al. 3P-EKE protocol

Attack

This section exhibits the detectable online password guessing attack on Raj et al. 3P-EKE Protocol. An invader Carol can copycat Alice and connect with Bob. While Bob is thinking that it is talking with Alice but actually it is talking with the invader Carol.

The details of attack are as follows:

Step 1: Alice generates two random numbers viz., RE a, r_a Є_R Z_p to compute M_a=g ^REa (mod p) & K_at=M_a ^ra (mod p) and then calculates E_Pwda(K_at © M_a), h_t(M_a © Id_a) & f Ka _t(M_a) and sends these credentials to Trusted Party.

• i .e., Alice © Bob : {Id a Id b Id t E Pwda (K t © M a ), h t (M a © Id a ), f Kat (M a )}

Step 2: Let an attacker Carol interrupts and intercepts the message {Id a, Id b, Id t, E Pwda (K t © M a ), h t (M a © Id a ), f Kat (M a )} and generates her own two random numbers viz., RE a’ ,r a’ Є R Z p to compute M a’ =g ^REa’ (mod p) & K at’ =M a’ ^ra (mod p). Now attacker Carol guess Alice’s password as Pwd a’ to encrypt E_Pwda ’ (K_at ’ © M_a ‘ ).Again she also computes the another two credentials h_t(M_a © Id_a) & f Kat’ (M a’ ) by its own because the Id’s are not secret and sends {Id a, Id b, Id t, E pwda’ (K at’ © M a’ ), h t (M a’ © Id a ), f Kat’ (M a’ )} to Trusted Party.

i.e., Carol ^ Trusted   Party :    {Id a,   Id_b ,    Id_t ,

E Pwda’ (K at’ © M a’ ), h t (M a’ © Id a ), f Kat’ (M a’ )}       ’      ’      ’

Step 3: Trusted Party decrypts E_Pwda ’ (K_at ’ © M_a ‘ ) to get (K_a t’ ® M_a ’ ) and also retrieves (M_a ‘ © Id_a) from h_t(M_a ‘ © Id_a) by using trapdoor after receiving the credentials {Id_a, Id_b, Id t, E pwda’ (K at’ © M a’ ), h t (M a’ © Id a ), MM - )} from’ an attacker Carol and computes M_a ‘‘ =( M_a ‘ © Id_a) © Id a to obtain K_at ’’ = K_at ‘ © M_a ‘ © M a''. Now Trusted Party verifies whether computed f_Kat’’(M_a’’) and received f_Kat’ (M a’ ) are equal or not. If both f_Kat’’(M a’’ ) & f_Kat’(M_a’) are equal then the guessed password is right and Trusted Party will continue with the remaining procedure of the protocol by assuming that he is in secured zone. In this way an attacker Carol may succeed in her attempt to attack.

Alice             Catherhie(Intruder)            Trusted Part)'                 Bob

(Id^IdbldtE^KbeMb), ьм®МьХЫМь))

Chooses RE3 ,raeRZp compute Ma = g™3 (mod p), and then Kar—Ma=n(mod p)

Guess password Pwda-

Encrypts Ерд^ХКщ-еМа-)

{IdJdbAEtwXK^Ma,

ВД- @1<у, ^(M,.)}

Decrypts Ep^da’ (KafSMa ) and obtains (Kal-®Ma=)’ Obtains (Ma-SIdJ from htfMgdlda)

Obtains K^^ Кэт@Ма-® M,» Verify feaM)

Checks fe^tM,»^ fe^ (Ma.) If equal Continue with residual procedure

Otherwise, Trusted Party terminates the Protocol at current session

Fig.4. Detectable Online Password Guessing Attack on Raj et al.3P-EKE Protocol

If both fKat’’(Ma’’) and fKat’(Ma’) are not equal, then the attack can be detected by Trusted Party. And the Trusted Party terminates the protocol for current session. An intruder never sits idle. After some time she repeats the same process. She will continue this until she hits the successful password. In this way a malicious user can impersonate the actual user by getting the secrete session key successfully. Fig 4 illustrates the detectable online password guessing attack on Raj et al. protocol.

• IV. Proposed Password authenticated 3P-EKE Protocol

In order to disregard the detectable online password guessing attacks, this paper endeavors to propose a secure Three-Party Encrypted Key Exchange (3P-EKE) Protocol based on XOR operation with analogous (parallel) message transmission. By using XOR operator and analogous message transmission, the proposed protocol makes it highly secure and improve the efficiency of transmission round. The detailed procedure of the proposed protocol is described in different steps as follows:

• i .e., Alice ^ Trusted Party: {Id a , Id_b, Id_t, E_Pwda(M_a © r_a), h t (Pwd a © M a ), f Kat (M a )}.

Step 2: Simultaneously, Bob also generates two random numbers viz., RE_b r_b ∈ _R Z_p to compute M_b=g ^REb mod p & K_bt=M_b ^rb mod p. Finally, he calculates E Pwdb (M b © r b ), h t (Pwd b © M b ) & f Kbt (M b ) and transfers {Id a , Id b , Id t , E pwdb (M b © r b ), h t (Pwd b © M b ), f ^bt (M b )} to Trusted Party.

• i .e., Bob ^ Trusted Party: {Id a , Id_b, Id_t, E_Pwdb(M_b © r_b), h t (Pwd b © M b ), f Kbt (M b )}.

Step 3: After receiving the messages sent from Alice and Bob, Trusted Party utilizes a trapdoor [15] to obtain Pwd_a © M_a & Pwd_b © M_b from h_t(Pwd_a © M_a) & h_t(Pwd_b © M_b) and computes M_a=Pwd_a © M_a © Pwd_a & M_b= Pwd_b © M_b © Pwd_b respectively. Now, Trusted Party decrypts E Pwda (M a © r a ) & E Pwdb (M b © r b ) and obtains

whether computed value f Kat (M a ) (or f Kbt (M b )) and received value f Kat (M a ) (or f Kbt (M b )) are identical or not. If this verification is passed, then it continues with the residual procedure of the protocol. Otherwise, Trusted Party terminates the protocol.

Finally, Trusted Party generates random exponent RE_t ∈ _R Z_p to compute M_b ^REt mod p & M_a ^REt mod p and calculates the hashed credentials f Kat (Id a , Id b , K at , M b ^REt ) & f Kbt (Id a , Id b , K bt , M a ^REt ). Finally, Trusted Party sends these credentials to Alice and Bob simultaneously.

i.e., Trusted Party ^ Alice: M_b ^REt , f_Kat(Id_a, Id_b, K_at, M b ^REt )} and

Trusted Party ^ Bob: { M aR ^Et ,f Kbt (Id a , Id b , K bt , M aREt )}

Step 4: Now to authenticate the Trusted Party, Alice & Bob verifies the received credentials f Kat (Id a , d b , K at , M b ^REt ) & f Kbt (Id a , Id b , K bt , M a ^REt ) respectively from it. If this verification does not hold, Alice and Bob terminate the protocol accordingly.

If this verification holds, Alice computes the session key SK=( M_b ^REt ) ^REa (mod p) & f_SK(Id_a,SK) and sends it to Bob. Similarly Bob computes the session key SK=(M_a ^REt ) ^REb (mod p) & f_SK (Id_b, SK) and sends it to Alice.

i.e., Alice ^ Bob: f_SK (Id a , SK) and

Bob ^ Alice: f_SK (Id_b, SK).

Step 5: After verification of the incoming messages f_SK(Id_b, SK) & f_SK(Id_a, SK) from the other side, both Alice and Bob can ensure that they actually share the secret session key SK=( M_b ^REt ) ^REa (mod p) = (M_a ^REt ) ^REb (mod p) for the current session. Otherwise, the protocol will be terminated. Fig 5 illustrates the proposed 3P-EKE Protocol.

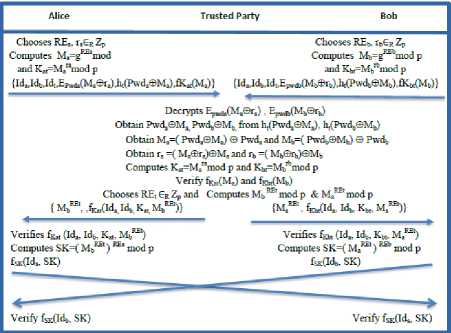
Fig.5. Proposed Password Authenticated 3P-EKE Protocol

• V.    Security and Performance Analysis

After careful revision and implementation of the proposed protocol, it is understood that the protocol is not only secure but highly efficient and also meets the given security requirements. The detailed analysis is presented in the following sections.

• A.    Security Analysis

The security analysis has shown that the proposed protocol is secure and robust to face any kind of possible password guessing attacks. The proposed protocol has successfully demonstrated its capabilities by meeting the necessary security requirements as follows:

• i.    Mutual Authentication

First: Alice & Bob use the trapdoor function h t to hide the random number & password i.e., (REa ⊕ Pwd_a) and (RE_b ⊕ Pwd_b) respectively. Trusted Party needs a corresponding password to decrypt M_a ⊕ r_a & M_b ⊕ r_b respectively. Since, only Trusted Party knows the trapdoor t and passwords Pwd_a & Pwd_b they can very well authenticate Alice & Bob after receiving the messages sent in step1 & step2 of the proposed protocol.

Second: Trusted Party sends {M b ^REt , f Kat (Id a , Id b , K at , M b ^REt )} to Alice & { M a ^REt ,f Kbt (Id a , Id b , K bt , M a ^REt )} to Bob in step 3 of proposed protocol. These messages can be used to authenticate the Trusted Party by Alice & Bob respectively.

Third: Alice & Bob derive key from M a ^REt & M b ^REt respectively, as mentioned in step 4 of the proposed protocol. With the help of f SK (Id b , SK) & f SK (Id a , SK) both Alice & Bob can authenticate each other respectively.

• ii.    Resistance to the Password Guessing Attacks

Attack Situation 1: A malevolent user Bob wants to mount undetectable online password guessing attacks on the proposed protocol.

A malicious attacker may try to guess the password with undetectable online password guessing attacks. If that is the case, the mutual authentication step is not possible. If Bob tries to guess Alice’s password, then Bob should perform the following procedure to mount an undetectable online password guessing attack. Bob obtains (M_a ⊕ r_a)* by decrypting E_Pwda(M_a ⊕ r_a) with a guessed password Pwd a *.

Next, he selects his random exponent RE b and computes M_b=g ^REb mod p and K_bt=M_b ^rb mod p to find h t (Pwd b ⊕ M b ),      f Kbt ((M a ⊕ r a )*)      and      sends

{E Pwda ((M a ⊕ r a )* ⊕ M b ), h t (Pwd b ⊕ M b ), f Kbt ((M a ⊕ r a )*)} to Trusted Party. Trusted Party authenticates the clients and sends {M b ^REt , f Kat (Id a , Id b , K at , M b ^REt )} to Alice and {M a ^REt , f Kbt (Id a , Id b , K bt , M a ^REt )} to Bob. Now client Bob intercepts {M b ^REt , f Kat (Id a , Id b , K at , M b ^REt )} but cannot compare any two terms and verify whether the guessed password is correct or not. Hence, Bob cannot mount an undetectable online password guessing attack on the proposed 3P-EKE protocol.

Attack Situation 2: A malicious user Carol wants to mount Detectable online password guessing attacks on the proposed protocol.

An attacker may try to guess the password with detectable online password guessing attack. She guesses password Pwd a * or Pwd b * to impersonate Alice or Bob. She chooses her own random exponent RE a or RE b and computes M=g ^REb mod p or M_b=g ^REb mod p. Now she selects a random number r_aor r_b to compute K_at=M_a ^ra mod p or K_bt=M_b ^rb mod p and then sends the credentials {E Pwda *(M a ⊕ r a ),     h t (Pwd a ⊕ M a ),     f Kat (M a )}     or

{E Pwdb *(M b ⊕ r b ), h t (Pwd b ⊕ M b ), f Kbt (M b )} to Trusted Party. Trusted Party will decrypt   E Pwda *(M a ⊕ r a )   or

E Pwdb *(M b ⊕ r b ) and gets (M a ⊕ r a )*or (M b ⊕ r b )*. Now M a or M b will get from h t (Pwd a ⊕ M a ) & Pwd a or h t (Pwd b ⊕ M b ) & Pwd b . Trusted Party computes r a = (M a ⊕ r a )* ⊕ M a or r b = (M b ⊕ r b )* ⊕ M b and finds K at =M a ^ra mod p or K bt =M b ^rb mod p to determine f Kat (M a ) or f Kbt (M b ). But the computed hash values will not be equal to the received hash values. Hence Trusted Party can detect this attack and take the counter measure. Hence, it is impossible for an attacker to mount detectable online password guessing attack.

Attack Situation 3: A malicious user Carol wants to mount off-line password-guessing attack on the proposed protocol.

An attacker may try to mount off-line password guessing attack to guess the password. She intercepts {E Pwda (M a ⊕ r a ), h t (Pwd a ⊕ M a ), f Kat (M a )} and may guess a password, extracts M_a ⊕ r_a, but it is impossible for her to get M a until trapdoor is known, which is known only to Trusted Party. This implies that she cannot verify the hash value f_Kat(M_a). Hence, offline password guessing attack on the proposed protocol is impossible.

Attack Situation 4: Carol wants to get the session key SK.

Carol may want to get the session key SK agreeing to either f SK (Id a , SK) or f SK (Id b , SK). However, this approach cannot work, since it is very hard to retrieve a number according to the hashed value returned by the hash function.

Similarly, there might be a case that, an intruder Carol still cannot get the session key SK by impersonating the Alice/Bob or analyzing the transmitted data because of the same reasons mentioned already.

Trivial Attack

An attacker Carol may directly try to compute the session key from M a ^REt or M b ^REt . However, due to the one-way hash function and the intractability of the Discrete Logarithmic Problem (DLP), the trivial attack is not possible on the proposed protocol.

Pre-play attacks

An intruder Carol may impersonate Alice to cheat Bob to get the essential information for making Bob convinced that Carol is Alice. However, Carol cannot succeed, since Pwd a & Pwd b are unknown to it. Hence, she will encounter the same difficulties as already mentioned.

Replay Attacks

Suppose that Carol intercepts the message {Id_a, Id_b, Id_t, E Pwda (M a ⊕ r a ), h t (Pwd a ⊕ M a ),f Kat (M a )} send by Alice to cheat Trusted Party. Carol cannot cheat trusted party, because Alice chooses a random number r a whenever Alice wants to communicate with Bob to perform the password authenticated key exchange protocol. If an attacker Carol just sends {Id a , Id b , Id t , E Pwda (M a ⊕ r a ), h_t(Pwd_a ⊕ M_a), f_Kat(M_a)}, then Trusted Party will detect the attack easily, since Pwd a ’s & r a ’s are different all the time. Consequently, an intruder Carol cannot perform replay attacks successfully.

Man-in-the-middle Attack

Suppose the attacker Carol frames her own message i.e. {EPwdc(Mc⊕rc), ht(Pwdc⊕Mc), fKct(Mc)} with the guessed password Pwdc and sends it to trusted party. The trusted party will decrypt EPwdc(Mc⊕rc) to get (Mc⊕rc)’ and obtains ‘Pwdc⊕Mc’ from ht(Pwdc⊕Mc). Hence carol in the middle cannot obtain the correct Mc until its guessed password is correct. Finally, Trusted Party computes hash value which will not match with the received hash value. Hence the protocol gets terminated by not allowing man-in-the-middle to mount any attack.

Server Spoofing

The trusted party computes f Kat (Id a , Id b , K at , M b ^REt )} & f Kbt (Id a , Id b , K bt , M a ^REt ) and sends to Alice and Bob, respectively. Now, Alice and Bob can authenticate the trusted party by computing f_Kat(Id_a, Id_b, K_at, M_b ^REt )} & f_Kbt(Id_a, Id_b, K_bt, M_a ^REt ) respectively. Thus, the Carol cannot imporsonate the trusted party to deceive the client.

Perfect Forward Secrecy

The proposed protocol has the perfect forward secrecy.The session key is computed asfollows: SK= ( M b ^REt ) ^REa (mod p)=(M a ^REt ) ^REb (mod p). If the Carol gets {M b ^REt , f Kat (Id a , Id b , K at , M b ^REt )} or {M a ^REt , f Kbt (Id a , Id b , K_bt, M_a ^REt )}, then in order to obtain the session key, she should know RE_b or RE_a. The session keys generated in different sessions are independent, since RE a and RE b are randomly chosen by Alice and Bob, respectively. This indicates that Carol cannot obtain previous session keys even if she obtains the session key used in this run.

Known-Key Security

The proposed protocol assumes that, REa and REb are randomly chosen by Alice and Bob and are independent among protocol executions. This leads to the invulnerability of Known-Key security.

• B.    Performance Analysis

The development of an efficient protocol should take the number of transmission rounds and the computation complexity into account. The proposed protocol requires four message transmission rounds.

Transmission Round and Computation Complexity

Table 2 depicts the comparison of performance among Chang-Chang’s, Yoon-Yoo’s, PSRJ, Raj et.al and the proposed password authenticated 3P-EKE protocols. The invention or design of a proficient protocol should take the number of transmissions (though communication channel) and the complexity of computation into account. The proposed protocol requires (2, 2, 2) number of transmissions from Alice, Bob and Trusted Party respectively. From the table, it is quite obvious that there is no difference at all in complexity of computation among the well-known protocols and the proposed protocol.

The modular exponential operations are not increased due to the inclusion of XOR operation, since client Alice sends E Pwda (M a ⊕ r a ), h t (Pwd a ⊕ M a ) & f Kat (M a ) to Trusted Party and client Bob sends {E Pwdb (M b ⊕ r b ), h t (Pwd b ⊕ M b ), f_Kbt(M_b)} to Trusted Party. By imposing XOR operation between Pwd_a & M_a client Alice can enforce perfect security on the protocol and is the same case with Bob too. Trusted Party first utilizes a trapdoor to obtain (Pwd a ⊕ M a ) & (Pwd b ⊕ M b ) from h t (Pwd a ⊕ M a ) & h t (Pwd b ⊕ M b ) and then retrieves M a = Pwd a ⊕ M a ⊕ Pwd a & M_b= Pwd_b ⊕ M_b ⊕ Pwd_b respectively.

Now Trusted Party utilizes Pwd_a & Pwd_b to decrypt E Pwda (M a ⊕ r a ) & E Pwdb (M b ⊕ r b ) and gets (M a ⊕ r a ) & (M b ⊕ r b ). Then it retrieves the values r a= (M a ⊕ r a ) ⊕ M a & r b= (M b ⊕ r b ) ⊕ M b and then computes K at =(M a ^ra mod p) & K_bt=(M_b ^rb mod p) accordingly and verifies whether computed value f_Kat(M_a) (or f_Kbt(M_b)) and received value f Kat (M a ) (or f Kbt (M b )) are identical or not. A total four modular exponential operations are required for the execution of the proposed protocol, which also preserves the computation complexity. The first two modular exponential operations are required for authentication of the clients, while the remaining two modular exponential operations for sending the message to the corresponding clients (Alice and Bob).

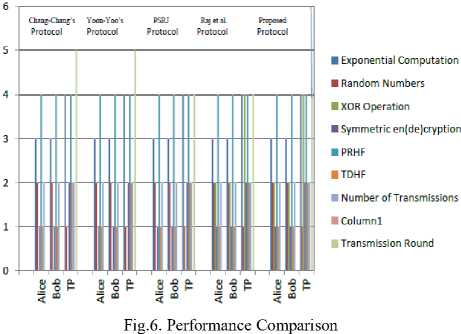
The comparison of computation complexities among four 3P-EKE Protocols viz., Chang-Chang’s, Yoon-Yoo’s, PSRJ, Raj et.al protocols against the proposed password authenticated 3P-EKE protocol is illustrated in Fig 6.Similarly, Table 2 demonstrates the comparison between different types of attacks such as Chang-Chang’s, Yoon-Yoo’s, PSRJ, Raj et.al protocols as against the proposed password authenticated 3P-EKE protocol. From the table it can be noticed that the proposed protocol is invulnerable to various attacks as mentioned earlier.

Table 2. Performance Analysis of Various 3P-EKE Protocols

ЗР-ЕКЕ Protocols ■► Participants Computation Type & ■ Attack Type 4-	Chang-Chang's protocol	Yoon-Yoo;s protocol	PSRJ protocol	RajetaL protocol	The Proposed protocol
	Alice Bob TP	Alice Bob TP	Alice Bob TP	Alice Bob IP	Alice Bob TP
Exponential Computations	3 3 4	3 3 4	3 3 4	3 3 4	3 3 4
Random numbers	2 2 1	2 2 1	2 2 1	2 2 1	2 2 1
Exclusive OR Operation	0 0 0	0 0 0	0 0 0	2 2 4	2 2 4
Symmetric en(de)ciypnon	1 1 2	1 1 2	1 1 2	1 1 2	1 1 2
Pseudo Random hash Function(PRHF)Operations	4 4 4	4 4 4	4 4 4	4 4 4	4 4 4
Trapdoor hash functions (TDHF) Operations	1 1 2	1 1 2	1 1 2	1 1 2	1 1 2
Number of Transmissions	2 2 2	2 2 2	2 2 2	2 2 2	2 2 2
Transmission Round	5		4	4	4
Undetectable Online Password Guessing Attack	YES	YES	YES	YES	NO
Detectable Online password Guessing Attack	YES	YES	YES	YES	NO
Off-line Password Guessing Attack	YES	YES	YES	YES	NO

• VI.    Conclusion