Design of a Web Interface for Fractional Chaotic Systems

Published Online December 2014 in MECS DOI: 10.5815/ijcnis.2015.01.07

Briefly, a chaotic system can be defined as a system that demonstrates commitment to precise initial conditions. An immeasurable change of chaotic systems’ initial condition may cause immeasurable changes at system’s future conditions. Two points worth to note here; one is that future states of the system vary firmly and precisely with the initial conditions, and the other is that the system becomes complicated with the increasing number of variables [1]. It is important to stress that chaos is not a random concept. Chaotic systems, even unconsciously, evaluate all entries they put out a final behavior according to them. A large number of variables are available that the essential factor makes environment more chaotic [1]. Chaotic systems are not the systems that only can be created under laboratory conditions or produced in intellectual. In fact, the physical and nonlinear structures in our lives all have the potential to show chaotic behavior.

Different software tools are used to get practical chaotic systems having visibility feature. To mention a few notable studies among others, Uyaroğlu and colleagues have implemented simulations of these equations using MATLAB and Simulink, which turned out performance graphs [2]. Pacheco and colleagues have presented a new CAD tool using MATLAB GUI by the way of behavioral modelling to automatically perform the synthesis of chaotic systems [3]. Besides, there are also studies for the one-dimensional and three-dimensional chaotic systems visual analysis with MATLAB GUI [4,5]. Trzaska performed MATLAB and PSPICE simulations of fractional order chaotic circuits [6].

MATLAB provides a great number of functions and options for the visualization of data. The main advantage of MATLAB is the easy use and supported tools. In MATLAB, graphs are shown in a figure window. While one is active, several windows can be displayed. Performed operations can be seen in active figure.

From the viewpoint of mobility studies and dissemination to large number of users, the drawback is that MATLAB software requires to be installed on the computer of each user. In order to eliminate this disadvantage more flexibly structured tools are necessary to utilize. For this purpose many studies have been completed using MATLAB Web Figure tools that allows you to use written functions [7, 8, 9, 10, 11]. In addition, Uyaroğlu and Varan have designed a web interface for the analysis of Chaos and non-linear chaotic structure of the power systems [1].

In this study, a web interface is designed which is a class of chaotic systems with orders of fractional derivative for the simulation of chaotic systems using MATLAB Builder NE and MATLAB Web Figures instruments. In Section 2, a review of fractional differential chaotic systems is provided. Also in this section the third part of tool and designed web interface are introduced. In Section 3 the results and evaluations are presented.

• II.    Fractional Chaotic Systems

Fractional systems have become so popular in recent years [1]. Various systems can be described by fractional differential equations, and demonstrates chaotic behavior [2, 4]. Recently, many engineers conducted researches that help to comprehend chaotic behaviors and chaotic control of dynamical systems [7, 8]. Chaotic systems

Paper Title: Preparations of Papers for the Journals of the MECS Publisher heavily depend on numeric parameters and it's conditions [10].

These systems are defined as integer number, noninteger number or mixed number order fractional systems. Although the emergence of fractional analysis was about

300 years ago, systematic works appeared in 19. century [12]. Intensive development of Fractional analysis was performed by Bertram Ross [13] after an international conference at the University of New Haven in 1974 [14]. Aftermath fractional analysis began to be widely used in many fields such as science and engineering applications, mathematics and physics circles, and so on [15,16].

General methods of analysis are based on integer order differentiation and integration process. But in real life, many dynamic system can be defined via fractional order systems based on fractional systems [17]. This mathematical phenomenon provides a more realistic definition of real-world objects than conventional methods of integer. Real-world objects are usually fractional [18, 19]. The main reason of using integerorder models is the lack of solution for fractional difference equations. While defining the real-world objects, we should use fractional degree models. The first advantage of this model is the use of high degree freedom. The second is that although integer-order systems have limited memory, fractional integer order systems have infinite memory [20].

In 1963, Meteorology expert Edward Lorenz published an article which showed that differential equations with three variables can constitute chaos. It also revealed that chaos has a regular structure. These studies had not made remarkable effect until the 1960s. Later on, many mathematicians and physicists started to work in the field of chaos that shed light on further studies [15, 39, 40, 41, 42]. Later, scientists began to explore about forming systems of differential equations which have different structures. The "butterfly effect" was observed by many people following the first examples by Lorenz as shown in (1) [21].

engineering and biology. This equation system has a nonlinear oscillator effect and used in many mechanical problem [24, 43, 44, 45, 46].

_d ( fo x ) _{x ( t )}

fT = a ( y (t ) - x ( t ) )

( fo y )

^-^ytl = Sx (t) - X (t) z (t)+гр (t)             (3)

( fo z )

= x ( t ) y ( t ) - e z ( t )

_d ( fo x ) _{x ( t ) dt} ( fo x )

= y ⁽ t )

_d ( fo y ) _{y ( t )}

= x(t) - ay (t) - x(t)3 + 5 cos(tot)

Lu and Chen developed a system, given by (5), which provides a wide range parameter exchanging and can produce different chaotic shapes [25].

d ^{( fox )} x ( t )

dt (fo, )   = a( y(t ) - x(t ) )

( fo y )

' = - x (t) z (t) + Лу (t)        (5)

_dt ( fo y )

_d ( fo z ) _{z ( t )}

(fOz)   = x ( t ) У ( t ) - ez ( t )

d ^{( fox )} x ( t ) _dt ( fo x )

_d ( fo y ) _{y ( t ) dt} ( fo y ) _d ( fo_z ) _{z ( t ) dt} ( fo z )

= ст ( y ⁽ t ) - x ⁽ t ) )

= x ⁽ t ) ( P ^- z ⁽ t ) ) ^- У ⁽ t )

= x ( t ) У ⁽ t ) - ^e z ⁽ t )

Arneodo chaotic model given in (2) was created to describe the dynamics of the three-layer convection [22].

_d ( fo x ) _{x ( t )}

—= y (t )

( fo x )

_d ( fo y ) _{y ( t ) dt} ( fo y )

= z ⁽ t )

( fo z )

_dt („,( ) = - a x(t) - S y (t) - Л ( t) + e x ( t) 4

Chen's chaotic system (3) was derived from the classical Lorenz system, which has advantage in the field of anti-control [23].

Duffing differential equation system (4) is a well-known non-linear equation system used in physics,

In this study, two software tools are utilised as the basis for the design of the interface. One is Visual Studio 2010 which is used for carrying out the design and the other is MATLAB that used for mathematical operations and graphics drawing. With Visual Studio 2010 different languages such as C#, C++, Visual Basic, J# and ASP.Net programming is possible to perform a visual programming. However Windows and web-based applications can be made with this tool. Using this feature an ASP.NET based design is realised with Visual Studio 2010 for web interface in this work. The required codes have been written in C# language for the realization of dynamic processes in the web interface.

MATLAB program, which is very flexible and easy-to-use, is benefited for graphical visualization of the results of the fractional derivative transactions related to chaotic systems in designed web interface. For this reason, primarily necessary MATLAB codes are written in functions and used by compiling with MATLAB Builder NE. MATLAB Web Figure tool is used in the operation of displaying obtained results with charts.

MATLAB Builder NE tool renders MATLAB functions created in MATLAB possible to be used in different .NET platforms. This tool works in conjunction

with MATLAB Compiler and constitutes .NET extension components. For the constituted components to work seamlessly, MATLAB program does not need to be fully loaded on application computer to perform. Only MCR (MATLAB Compiler Runtime) should be installed which runs MATLAB commands. MATLAB Web Figure tool is also what exists in MATLAB Builder NE tool and ensures using of MATLAP graphics in web applications. This tool can be used in ASP.NET web site via adding to Visual Studio.

• A.    ynamic Systems

A dynamic system is a set of rules that explain the next state. A function of dynamic system is symbolized as f acting on U space. The f: U → U tells the belonging of an initial point to U as x0 ∈ U:

x n+1 = f(x n ), n ∈ N.

Generally the use of the notation is as f0(x0) = x0; fn+1(x0) = f(fn(x0)). Following iterates {fi(x)}∞ i=0 is called the forward factor of x. If any inversion is not possible forward is {f- i(x)}∞ i=0. while this operation time is considered as discrete [41,42,50]. The time variable is paired and consequently dynamic system is:

(t0, x0), (t1, f(x0)), . . . , (tn, fn(x0)), . . .

Linear differential equations is that include analytic solutions and provide well-defined asymptotic behavior as t → ∞. By contrast, if there is a simple situation that tells notions including bilinear, quadratic, result hard behaviors. Ergodic flows behave like thermodynamic systems in that invariant measures cause statistical ensembles.

The following non-linear system of differential equations, called as, x1 = - σx1 + σx2

x2 = x1 - x2 - x1x3

x3 = - βx3 + x1x2,

Various works have been done including Lorenz equations, see [27, 28, 29, 30]. As a finite model of atmospheric dynamics, these equations led Lorenz to the discovery of sensitive dependence of first conditions.

Here classical parameter values σ = 10, β = 8/3, each fixed point C± has a pair of complex eigenvalues with positive real part, and one real, negative eigenvalue. The origin is an odd point with two negative and one positive eigenvalue [36, 37, 38] satisfying

0 < - λ3 < λ1 < - λ2.

Thus, the stable manifold of the origin Ws(0) is twodimensional, and the unstable manifold of the origin Wu(0) is one-dimensional. We also note that the flow contracts volumes at a considerable rate.

• B.    Introducing The Web Interface

The web interface has been designed for five different chaotic system mentioned above. The first entry is a page of the web interface, as shown in Fig. 1. As can be seen in Fig. 1 there is not any result graphics and MATLAB Web Figure symbols are on compartments formed of graphics. On this page "OK" button is pressed by selecting drop-down list box of the chaotic system which will carry out the analysis.

If the Lorenz chaotic system is selected from the list shown in Fig. 2 mathematical model system page opens. In the system model it should be stated which model belongs to which system. Two parts called "Parameters" and "Fractional-Order" are under the system model section. In "Parameters" section the system model parameter values and in "Fractional-Order" section, fractional derivative model orders are determined. Under these two sections the "Initial Values" box to input initial values and “Phase Portraits" box exist to get the graphics.

Fig. 1. The opening page when the interface is entered.

WEB INTERFACE FOR FRACTIONAL CHAOTIC SYSTEMS

Please Select A System:          —

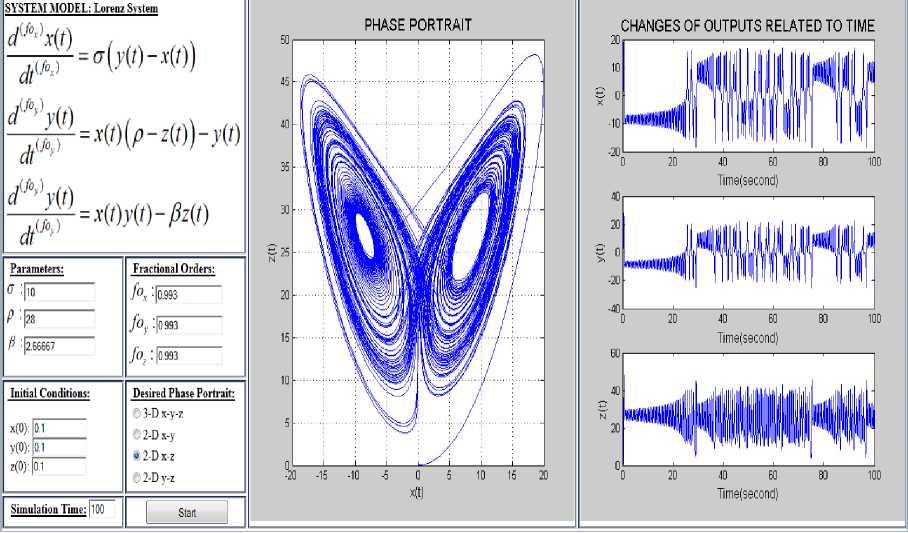
Fig. 2. Xz (2-D) Phase portrait and output graphics of the Lorenz chaotic system.

In "Simulation Time" pane run time input is entered in seconds. After all entries are made, the results are obtained and graphs are drawn via pushing "Start" button.

Fig. 2 shows, an x-z phase portrait, drawn for 100 sec in the form of 2-D, of a Lorenz chaotic system with varying degrees of fractional derivatives. In Fig. 3, 3-D phase portrait are provided for all the state variables using the same parameters. In Fig. 4 phase portraits and output graphics are provided for an Arneodo chaotic system [31, 32].

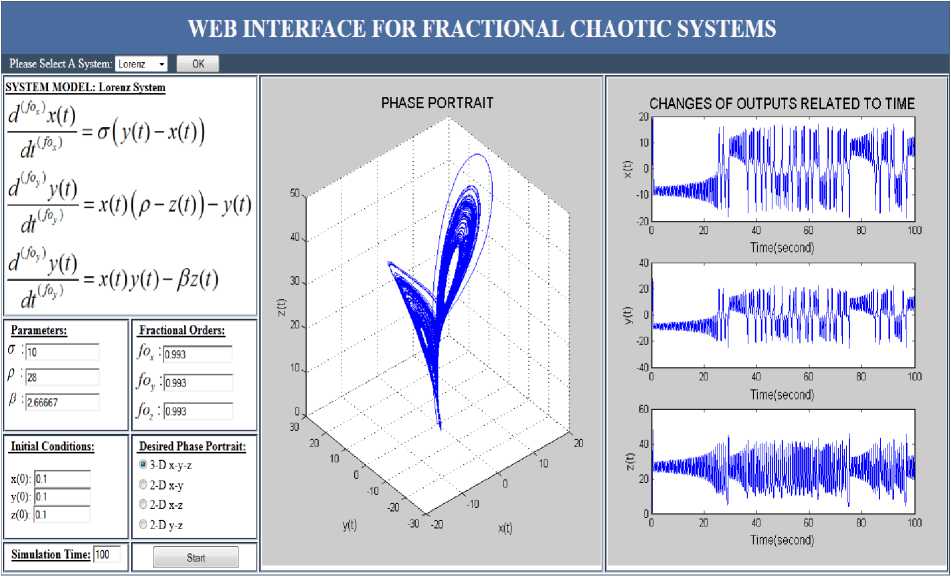
Fig. 3. X-Y-Z (3-D) phase portrait and output graphics of Lorenz chaotic system.

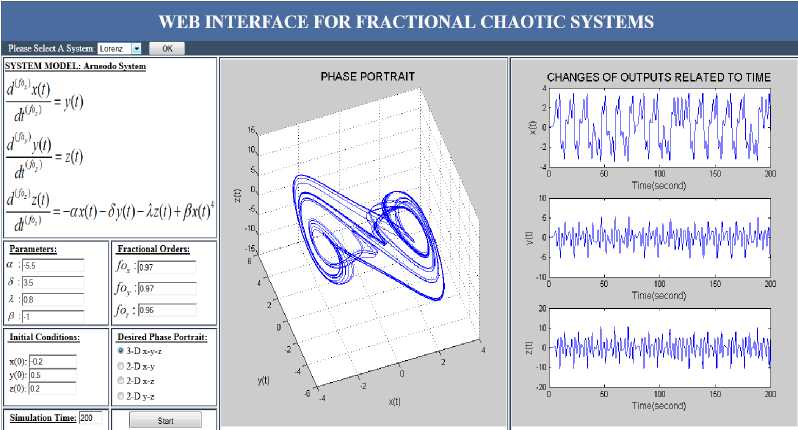
Fig. 4. X-Y-Z (3-D) phase portrait and output graphics of Arneodo chaotic system.

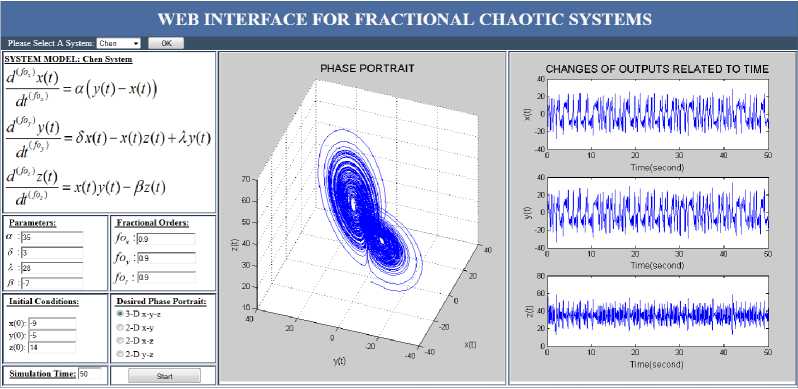
Fig. 5. X-Y-Z (3-D) phase portrait and output graphics of Chen chaotic system.

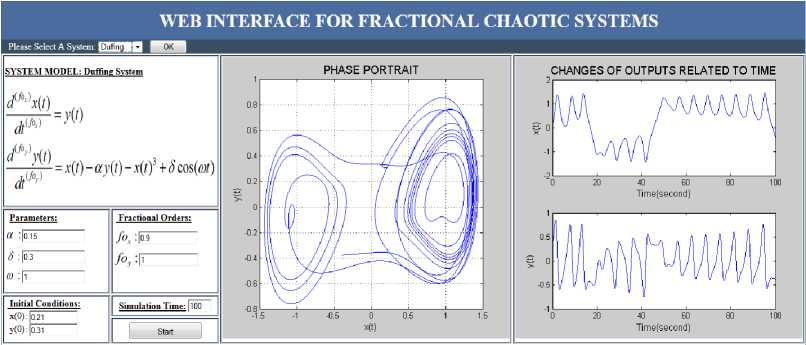
Fig. 6. X-Y (2-D) phase portrait and output graphics of Duffing chaotic system [33, 34, 35, 36].

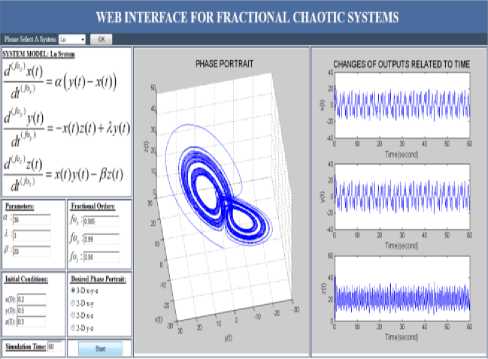
Fig. 7. X-Y-Z (3-D) phase portrait and output graphics of Lu chaotic system.

Here we present the realization of a useful and understandable design of an interface for the training analysis of chaotic systems. The design avoids the process complexity encountered for users to obtain the results and graphics. In addition, it is shown that the created interface can be used not only for educational purposes but also for engineering application for chaotic systems. Since the modelling of fractional derivative systems cannot be fulfilled with only tools such as MATLAB Simulink, the interface is implemented in a programmatic approach together with a visual property. Another virtue of the developed interface is the web interface feature which has the ability to serve multiple users. The usage range of the interface, which has been created for five different chaotic system, can be extended by adding different other chaotic systems.

• [27]    Akgul, A., Cetin, O., & Akar, F. (2011, April). High secure infrared communication application. In Signal Processing and Communications Applications (SIU), 2011 IEEE 19th Conference on (pp. 474-477). IEEE.

• [28]    Amigó, J. M., Kocarev, L., & Szczepanski, J. (2007). Theory and practice of chaotic cryptography. Physics Letters A, 366(3), 211-216.

• [29]    FINDIK O.: "Şifrelemede Kaotik Sistemin Kullanlmas"; M.S. thesis, Comp. Dept., Seluk. Univ., Konya., (2004).

• [30]    F. E. Yardm, E. Afacan: "SIMULATION OF A COMMUNICATION SYSTEM USING LORENZBASED DIFFERENTIAL CHAOS SHIFT KEYING (DCSK) MODEL ": J. Fac. Eng. Arch. Gazi Univ, 25, 1, (2010) 101-110.

• [31]    Lian, S. (2009). Efficient image or video encryption based on spatiotemporal chaos system. Chaos, Solitons & Fractals, 40(5), 2509-2519.

• [32]    Özkaynak, F., Özer, A. B., & Yavuz, S. Kaos Tabanlı Yeni Bir Blok Şifreleme Algoritması. BİLDİRİLER KİTABI, 108.

• [33]    Sobhy, M. I., & Shehata, A. R. (2001, May). Chaotic algorithms for data encryption. In IEEE INTERNATIONAL CONFERENCE ON ACOUSTICS SPEECH AND SIGNAL PROCESSING (Vol. 2, pp. II-997). IEEE; 1999.

• [34]    Ogras H., Turk M., Ogras S.: "Kaos tabanlı saysal csk ve dcsk    modlasyontekniklerinin    MATLAB/simulink

  ortamnda gerekletirilmesi"; IV. letiim Teknolojileri Ulusal Sempozyumu, (2009).

• [35]    G. TROULLINOS:  "A SOFTWARE BASED

  APPROACH TO SECURE VOICE APPLICATIONS"; Proceedings of the Third IEEE International Conference on Electronics, 1, (1999) 176182.

• [36]    House, B., Malkin, J., & Bilmes, J. (2009, April). The VoiceBot: a voice controlled robot arm. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (pp. 183-192). ACM.

• [37]    Rudžionis, A., Ratkevičius, K., Dumbliauskas, T., &

  Rudžionis, V. (2008). Control of computer and electric devices by voice. Elektronika ir elektrotechnika, 6, 11-16.

• [38]    Ferreiros, J., Pardo, J. M., De Córdoba, R., Macias-Guarasa, J., Montero, J. M., Fernández, F., & González, G. (2012). A speech interface for Air Traffic Control terminals. Aerospace Science and Technology, 21(1), 715.

• [39]    Zelditch, Steven. "On a “quantum chaos” theorem of R. Schrader and M. Taylor." Journal of functional analysis 109.1 (1992): 1-21.

• [40]    Akhiezer, Aleksandr Ilʹich, V. I. Truten, and N. F. Shul'Ga. "Dynamic chaos in the motion of charged particles through a crystal." Physics Reports 203.5 (1991): 289-343.

• [41]    Davis, Peter. "Application of optical chaos to temporal pattern search in a nonlinear optical resonator." Japanese journal of applied physics 29.7A (1990): L1238.

• [42]    Nozawa, Hiroshi. "A neural network model as a globally coupled map and applications based on chaos." Chaos: An Interdisciplinary Journal of Nonlinear Science 2.3 (1992): 377-386.

• [43]    Nara, Shigetoshi, and Peter Davis. "Chaotic wandering and search in a cycle-memory neural network." Progress of Theoretical Physics 88.5 (1992): 845-855.

• [44]    Fischer, I., et al. "High-dimensional chaotic dynamics of an external cavity semiconductor laser." Physical review letters 73.16 (1994): 2188.

• [45]    Abuhaiba, Ibrahim SI, et al. "Image Encryption Using Chaotic Map and Block Chaining." International Journal of Computer Network and Information Security (IJCNIS) 4.7 (2012): 19.

• [46]    Khare, Ankur A., Piyush B. Shukla, and Sanjay C. Silakari. "Secure and Fast Chaos based Encryption System using Digital Logic Circuit." International Journal of Computer Network and Information Security (IJCNIS) 6.6 (2014): 25.