Design of Fast Fourier Transform Architecture for GF(24) with Reduced Operational Complexity

Published Online October 2016 in MECS

Fourier analysis is useful in converting a signal from its original domain into frequency domain and vice versa. The Fast Fourier Transform (FFT) algorithm designed for the complex field is not well-suited for the finite field. The FFT in the complex field has applications throughout the subject of signal processing [3]. Whereas, the FFT over the finite field have been widely used in cryptography and have applications in error correcting codes. The method for Fast Fourier Transform over the finite field (i.e. Galois Field) [2] [3] along with the architecture has been suggested in the paper. Galois Field is a field that contains a number of finite elements.

The suggested method consists of decomposing an original polynomial into a sum of linearized polynomials and evaluating them at a set of basis points [2]. The architecture designed in this paper is for GF(24). The Cyclotomic Fast Fourier Transform (CFFT) is useful in RS i.e. Reed-Solomon decoders to reduce the complexity of the decoder [4]. Because Reed Solomon code is cyclic in nature [15]. The CFFT proposed in [2] has low multiplicative complexity but they have high additive complexities. The FFT suggested in this paper can be used to perform the RS decoding which involves two time-consuming steps (Syndrome computation and Chien search). Chien search is a fast algorithm used in determining roots of polynomials defined over a finite field. The RS codes are capable of correcting random errors and multiple burst errors. This architecture can also be used to implement the Gao algorithm [14] which includes operations based on Fourier transform.

The design of architecture follows several steps which have been explained in a simplified manner in this paper. The architecture is designed in 4 stages. The architecture so designed is modified by  applying Common

Subexpression Elimination (CSE) Algorithm. CSE algorithm reduces the additive  complexity of the architecture. The language used for design is Verilog and has been implemented in the Xilinx ISE Design Suite.

The paper proceeds as follows. Section II covers basic notions and definitions of the Fourier transform and the method to determine cyclotomic cosets, along with the basic theory of Galois Field. Section III focuses on linearized polynomials and generation of the matrix. Section IV describes hardware architecture. The Common Sub-expression elimination Algorithm has been explained in section V. Section VI illustrates the architecture after applying CSE. And the paper concludes with the comparison between two architectures in section VII.

• II.    Definitions

• 2.2.    The elements can be estimated through:

• 2.3.    The cyclotomic cosets C_k over modulo n=2^m – 1 for GF(2^m) is calculated as:

The Fourier transform of a polynomial is the collection of elements.

The Fourier transform can be generated using [2] [10]:

f to = L^fto           (1)

is of degree f(x) = n-1 and n | (2m-1).

f^')    X.   и '^li                (2)

Here, j Є |0, n-1|.

C 0 = {0} ,

C k1 = { k 1 , k 1 2, k 1 2², ....., k 1 2^m 1 ^-1},

...........,

Ckl = { kl , kl 2, kl 22, ....., kl 2ml-1}, where ks ≡ ks2msmodn.(3)

• 2.4.    A linearized polynomial over GF(2^m) is a polynomial represented as:

Lto = X kx21(4)

It can be shown that L(x) satisfies L(a+b) = L(a) + L(b).

One useful representation of elements in Galois Field is m-tuple representation. Let α0 + α1α + α2α +....+α

α^m-1 be the polynomial representation of a field element β. Then, β can be represented by an ordered sequence of m components called an m-tuple, as follows [7]: (α 0 , α 1 , α 2 , . . . , α m-1 )

Where, the m components are simply the m coefficients of the polynomial representation of β.

For GF(24) the 4-tuple representation generated by p(X) = X4+X+1 is:

Table 1. 4-Tuple representation

Power representation	Polynomial representation	4-Tuple representation
0	0	(0 0 0 0)
1	1	(0 0 0 1)
α	α	(0 0 1 0)
α2	α2	(0 1 0 0)
α3	α3	(1 0 0 0)
α4	α+1	(0 0 1 1)
α5	α2+ α	(0 1 1 0)
α6	α3+ α2	(1 1 0 0)
α7	α3+α+1	(1 0 1 1)
α8	α2+1	(0 1 0 1)
α9	α3+α	(1 0 1 0)
α10	α2+α+1	(0 1 1 1)
α11	α3+α2+α	(1 1 1 0)
α12	α3+α2+α+1	(1 1 1 1)
α13	α3+α2+1	(1 1 0 1)
α14	α3+1	(1 0 0 1)

The elements of GF(2m) forms all the roots of X2^m + X. Let Ø(X) be the polynomial of the smallest degree over GF(2m). This polynomial Ø(X) is called the minimal polynomial of β. Ø(X) must be irreducible. Minimal polynomials of the elements in GF(24) generated by p(X) = X4+X+1 are:

Table 2. Minimal polynomials

Conjugate roots	Minimal polynomials
0	X
1	X+1
α, α2, α4, α8	X4+X+1
α3, α6, α9, α12	X4+X3+X2+X+1
α5, α10	X2+X+1
α7, α11, α13, α14	X4+X3+1

• III.    Cyclotomic Fast Fourier Transform

Based on the formula mentioned in (3) in section II, the cyclotomic cosets so formed for GF(24) after substituting m=4 i.e. n=15 are as follows:

C 0 = {0}

C 1 = C 2 = C 4 = C 8 = {1,2,4,8}

C 3 = C 6 = C 9 = C 12 = {3,6,9,12}

C 5 = C 10 = {5,10}

C 7 = C 11 = C 13 = C 14 = {7,11,13,14}

An irreducible polynomial p(X) of degree m is said to be primitive if the smallest positive integer n for which p(X) divides Xn+1 is n = 2m-1. p(X) = X4+X+1 divides X15+1 but does not divide any Xn+1 for 1 ≤ n ≤ 15. Hence, X4+X+1 is a primitive polynomial for GF(24). Let α be the root of this polynomial.

f(a') can be developed using:

№) = X = _Qa («^jkl))           (5)

These coefficients α ijs are used to form the matrix A. For example, in GF(2⁴) l=4, k 0 =0, k 1 =1, k 2 =3, k 3 =5, k 4 =7. So,

f(α¹) = L 0 (α⁰)+L 1 (α)+L 2 (α³)+L 3 (α⁵)+L 4 (α⁷)

= L 0 (1) + L 1 (β) + L 1 (β⁸) + L 2 (β) + L 3 (γ) + L 4 (β) + L 4 (β²) + L 4 (β⁴)

Here, the basis for C₁, C₃, C₇ is (β, β², β⁴, β⁸), where β = α³ and α is an element of GF(2⁴) as α = β + β⁸. For C 5 the basis is (γ, γ²) where γ = α⁵.

The coefficients of f(α1) are deduced as

α ijs = [1 1 0 0 1 1 0 0 0 1 0 1 1 1 0]

The rest of the equations are developed as follows:

f(α⁰) = L 0 (α⁰) + L 1 (α⁰) + L 2 (α⁰) + L 3 (α⁰) + L 4 (α⁰) f(α¹) = L₀(α⁰) + L₁(α) + L₂(α³) + L₃(α⁵) + L₄(α⁷)

f(α²) = L 0 (α⁰) + L 1 (α²) + L 2 (α⁶) + L 3 (α¹⁰) + L 4 (α¹⁴)

f(α¹³) = L 0 (α⁰) + L 1 (α¹³) + L 2 (α³⁹) + L 3 (α⁶⁵) + L 4 (α⁹¹)

f(α¹⁴) = L 0 (α⁰) + L 1 (α¹⁴) + L 2 (α⁴²) + L 3 (α⁷⁰) + L 4 (α⁹⁸)

Based on the above equations, the matrix A so formed is – г 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11

1 1 0 0 1 1 0 0 0 1 0 11 1 0

1 1 1 0 0 0 1 0 0 0 1 01 1 1

1 1 0 0 0 0 0 0 1 1 1 0 1 0 0

1 0 1 1 0 0 0 1 0 1 0 1 0 1 1

1 0 1 0 1 1 1 1 1 0 1 0 1 0 1

A =

1 0 1 0 0 1 0 0 0 1 1 00 1 0

1 1 1 1 0 0 1 0 0 1 0 01 1 0

г 1  1  0  1  1 y 10

• [1 0     01И11N

The complete architecture can be computed as [2]:

F = AQ(C . (Pf))(6)

Where, Q is the binary block diagonal matrix, C is the combined vector of constants, and P is the binary block diagonal matrix of combined pre-additions.

1 0 0 1 1 0 0 0 1 0 1 1 1 01

1 0 0 0 1 0 0 1 0 1 1 1 0 00

1 1 0 1 0 1 1111 0 1 0 1 0

1 1 1 0 1 1 0 0 0 0 1 1 1 00

1 0 0 1 0 0 1 0 0 1 1 0 0 01

1 1 0 1 1 0 0 0 1 1 0 1 0 01

-1 0 1 1 1 0 0 1 0 0 1 0 0 1 1 -

This matrix A is multiplied by the vector. The vector is denoted as Lf, where f is the original vector and L is the block diagonal matrix formed by elements β. The matrix L is represented as –

L = 0

-0

0    00

L2   00

0  L30

IV.   Hardware Architecture

The architecture design of FFT starts with the designing of GF multiplier. The GF multiplier is used for multiplication of polynomials [7].

Consider 2 polynomials (a₀a³ + a 1 a² + a2a + a₃) and (b₀a³ + b 1 a² + b2a + b₃).

The multiplication of these polynomials results in c0a3+c1a2+c2a+c3= (a0b0+a3b0+a0b3+a2b1+a1b2) a3 + (a0b0 +a1b0 +a0b1 +a3b1 +a1b3 +a2b2) α2 +( a1b1 +a0b1 +a2b0 +a0b2 +a1b1 +a3b2+a2b3) α + (a3b3 +a2b0 +a0b2 +a1b1 )

where

L1 = L2 = L4 =

and

0    0   /Л-

\^{p p 2} p4 Lp⁸

p 2  p4  p8p 4  p8p p 8  pp2

24-

The GF multiplier design can be represented as –

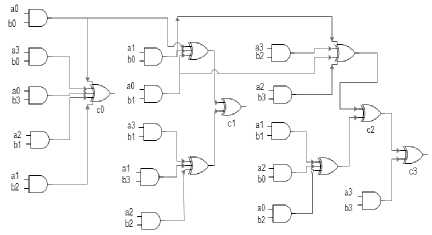
Fig.1. GF Multiplier

L3=£

Further, applying cyclic convolution between the normal basis and f_i i.e. Lf [2][5][6] is rewritten as [3] B = L f = Q ((R β i ^T).(S f i )) =

1111		1000
1100		1010
0011	rPl	1010
0101	R8	1001
1010		1100
1000	p	1111
0100	ipj	1111
0010		1111
-0001-		-1111-

Г/11 f 2 f 4

Lf 8j

This four point cyclic convolution [6] is obtained for cosets C 1 , C 3 , C 7. Whereas, the same interpretation for coset C 5 gives a two-point cyclic convolution.

The above design requires 16 AND gates and 8 XOR gates.

The complete FFT architecture [3] can be represented as follows:

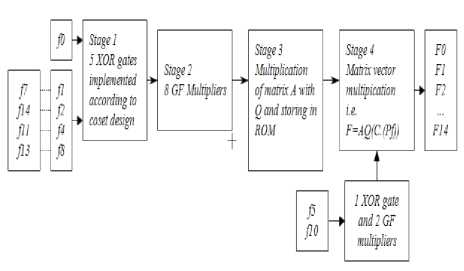
Fig.2. Architecture design

The cosets form the stage 1 and 2 of the architecture. The design for C₁, C₃, C₇ is same, whereas the design for C 5 is different. Cosets C 1 , C 3 , C 7 requires 5 XOR gates and 8 GF multipliers, whereas C 5 requires only 1 XOR gate and 2 GF multipliers. The design for cosets is:

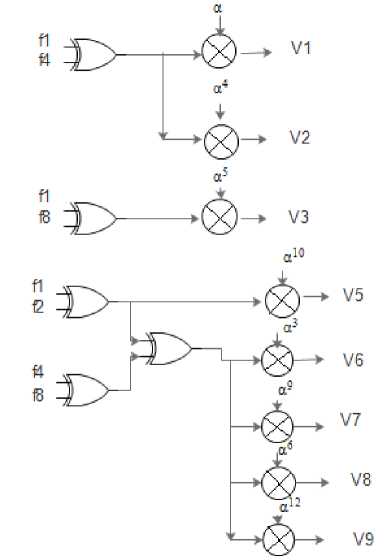
Fig.3. Coset design for C 1 , C 3 , C 7 .

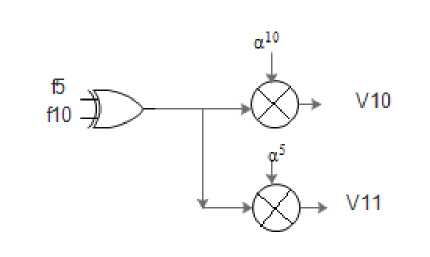
Fig.4. Coset design for C 5 .

In stage 3, the matrix multiplication is performed. The matrices A and Q are multiplied and thereby stored in ROM. The resultant matrix size is 15 x 31. Finally, in stage 4 the matrix and vector are multiplied. Stage 1 and 2 results in a vector, whereas stage 3 results in a matrix. The output of stage 4 is the FFT of the input.

• V. Common Sub-Expression Elimination Algorithm

In many Digital Signal Processing applications, multiple constant multiplication is widely used. In VLSI design for high-level synthesis, proper optimization of multiple constant multiplication is effective in improving parameters like area and power consumption. To optimize multiple constant multiplications, the Common

Sub-Expression Elimination (CSE) algorithm is used in this paper [5]. The approach used in CSE is initially to identify the identical terms i.e. the common subexpressions present in the equations and then to replace them with a single variable. Thus, by computing the terms only once, results are significantly being reduced in the hardware architecture in VLSI design.

In Galois field, matrix multiplication is performed. Here, the addition is performed via XOR-ing but there are several methods to perform multiplication. In this paper, the multiplication is a linear transform of the form C = AB, where C and B are m- and n- dimensional column vectors, respectively, and A is an m x n constant binary matrix. Here, B represents input variable and C represents output variables. According to this paper, the B column vector is (C . (Pf)) and the matrix A is the resultant matrix of AQ (Refer (6)). So, the CSE algorithm is applied to this matrix – vector multiplication.

Some general steps are involved in carrying out the CSE algorithm. These steps are as follows [5]:

• 1.    To identify common patterns present in the transformation.

• 2.    Select an appropriate pattern for elimination.

• 3.    Compute the pattern only once.

• 4.    Eliminate the occurrences of the computed pattern

• 5.    Repeat steps 1 to 4 to cover every pattern.

So, by applying CSE algorithm to matrix-vector multiplication there is a significant reduction in a number of XOR gates.

The method suggested in [8] reduces the additive complexities of Cyclotomic Fast Fourier Transform using a weighted sum of the numbers of multiplications and additions. [12] focuses on both area and delay optimization in hardware implementations over GF(2m).

• VI.   Reduced FFT Architecture

To reduce the additive complexity of the FFT architecture, in this paper, the CSE algorithm mentioned in section V has been used. The basic stages of architecture mentioned in section IV remain the same, with the only difference in being applying the CSE algorithm. The CSE algorithm is applied to stage 4. After applying the CSE algorithm to the matrix, the matrix size increases from 15 x 31 to 47 x 63. Due to this, the number of LUTs eventually increases in the final architecture but the additive complexity i.e. the number of XOR gates are reduced significantly.

We have written a synthesizable Verilog code for the different stages of the architecture. First 3 stages of the architecture remains the same, whereas, the architecture design changes at stage 4. Based on the appropriate changes the two architectures i.e. without CSE and with CSE can be compared in terms of LUTs, the number of XOR gates required and delay.

• VII.    Results

The complexity of the proposed architecture has been evaluated considering the synthesis report generated in Xilinx ISE Design Suite. The synthesis report has been generated for two FPGA devices, namely- Spartan 6 and Virtex 5. The results of the GF multiplier used in the architecture are- for Spartan 6 the LUTs required are 9 whereas for Virtex 5 the LUTs required are 8. Number of IOBs remains the same for both FPGA kits.

Table 3. Synthesis Report – GF Multiplier

XOR gates	LUTs required	IOBs	Max Combinational path delay
Spartan 6
4 1	9 1	12         1	6.781ns
Virtex 5
6 1	8 1	12         1	5.115ns

The maximum combinational path delay is the maximum delay that would occur for the complete architecture. For cosets C₁, C₃, C₇ since the design is the same the implementation results so generated are same. But, for coset C₅ the results are different. For cosets C₁, C 3 , C 7 te results are:

Table 4. Synthesis Report – Cosets C 1 , C 3 , C 7

XOR gates LUTs required IOBs Max Combinational path delay Spartan 6 37 88         1 80        1 8.379ns Virtex 5 52        1 80        1 80        1 5.969ns for cosets C1, C3, C7 the XOR gates required for Spartan 6 are 37 and for Virtex 5 are 52.

Table 5. Synthesis Report – Coset C 5

XOR gates	LUTs required	IOBs	Max Combinational path delay
Spartan 6
9 1	22          1	24          1	7.791ns
Virtex 5
13            1	20         1	24          1	5.715ns

The stage 3 of the architecture is formed by the multiplication of matrix A with Q. The simulation results are:

In the stage 3 of architecture, since only matrix multiplication is involved, no XOR gates are required in this stage.

Finally, the results for the architecture without applying CSE are:

Table 7. Synthesis Report – Architecture without CSE

XOR gates	LUTs required	IOBs	Max Combinational path delay
Spartan 6
121	360	100	10.893ns
Virtex 5
170	340	100	8.363ns

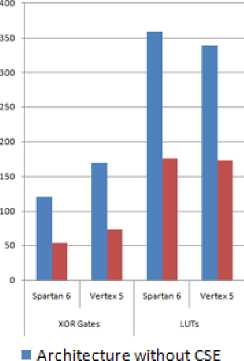
The paper mainly focuses on reducing the additive complexity of the FFT architecture. Therefore, the number of XOR gates required before modifying the architecture are 121 and 170 for Spartan 6 and Virtex 5 respectively.

The results after modifying the architecture with CSE are:

Table 8. Synthesis Report – Architecture with CSE

XOR gates	LUTs required	IOBs	Max Combinational path delay
Spartan 6
54         1	176        1	132	6.93ns
Virtex 5
73	173	132	9.849ns

After applying CSE, the number of XOR gates are reduced to 54 and 73 for Spartan 6 and Virtex 5 respectively.

• VIII.    Conclusion

It is clearly evident from the above-mentioned results that the additive complexity of the architecture after applying CSE reduces by a considerable amount. The area of the architecture is also reduced. The number of XOR gates required before applying CSE is 121 and 170 for Spartan 6 and Virtex 5 respectively. Whereas, after applying CSE XOR gates reduces to 54 and 73. Thus, the additive complexity of the FFT architecture is reduced.

Graphically, the comparison between two architectures can be plotted as:

Table 6. Synthesis Report – Matrix A*Q

LUTs required	IOBs	Max Combinational path delay
Spartan 6
31	35	6.1ns
Virtex 5
31          1	35          1	3.979ns

■ Architecture with CSE

Fig.5. Complexity comparison of architectures.

• IX.   Future Scope

This paper primarily focuses on FFT of 15 elements represented as GF(24). But, based on the technique mentioned in the paper, the FFT for higher powers of 2 can also be generated. To generate DFT over larger fields like GF(211) or GF(212), the algorithm mentioned in [11] can be used. Different multipliers like Karatsuba multiplier, Montgomery multiplier etc. can be used and compared with above-mentioned results.

Acknowledgment

The authors would like to thank Prof. P. Trifonov and Prof. S. Fedorenko for the details of the algorithm used in this paper. The authors would also like to thank Prof. Ali AL Ghouwayel, Prof. Yves Louët, Prof. Amor Nafkha and Prof. Jacques Palicot for the details of CFFT hardware architecture.