Design of Type 2- interval fuzzy PID controller for CSTR

Published Online October 2019 in MECS

In industries, as a whole, it is realized that the most normally utilized controllers are regular proportional– integral–derivative controller since they are basic in structure and low in cost [1]. In [2], different proportional–integral–derivative controller tuning strategies are testified i.e. Ziegler and Nichols, Cohen and Coon, Internal Model Control etc. Pole Placement Design Strategies are a portion of the outline systems. The use of proportional, integral and derivative controllers in controlling direct framework may be a successful approach to accomplish wanted execution, yet prop-integ-deriv (i.e. PID) controller would not give a palatable execution when the procedures have a questionable model or if the procedure is non-linear.

In [3] it is determined that Type 1- Interval Fuzzy Logic Controllers(T1IFLC) can be actualized with single or multiple inputs. Despite the fact that the significant research chip away at fuzzy prop–integ–deriv controller fixates is on the customary, either of the two inputs i.e. PI or PD. This sort of controller proposed by Mamdani, in various works. It demonstrates the solitary information that T1IFLC offers additional noteworthy adaptability and better useful properties. In three different sorts, fuzzy controllers are grouped: the gain scheduling, direct action (DA) sort, and a mix of DA and gain scheduling sorts. The DA sort generally utilized as a part of fuzzy prop– integ–deriv controller application; here in the criticism control circle fuzzy prop–integ–deriv controller is added, and the prop–integ–deriv controller activities computed utilizing fuzzy derivation. In gain scheduling sort controllers, singular prop–integ–deriv controller pick-ups are figured through fuzzy deduction.

As of late, the fundamental research concentrates on T2IFLC [4]. For the most part, T2IFLC finish prevalent exhibitions as it gives an extra level of the opportunity given by the impression of vulnerability in their Type-2 Interval Fuzzy Sets (T2IFS). Key contrasts between T2IFLC and T1IFLC are adaptive-ness, implying that the installed Type 1- Interval Fuzzy Sets (T1IFSs) used to register the limits of the type deduced interval change as input varies. The upper-side membership functions (UMF) and lower-side membership functions (LMF) of a similar T2IFS might be utilized at the same time in processing each bound of the type deduced interval. T1IFLC lack these properties, because of this a T1IFLC is unable to execute the intricate control surface of a T2IFLC utilizing a similar rule base. Interior structure of the T2IFLC is similar to T1IFLC. Principle distinction is desired fuzzy membership function (FM), yet advanced algorithms are developed for designing T2IFLC for generating the control surface [5]. The primary weakness of this approach is that it does not clarify how the footprint of uncertainty parameters influences the execution and robustness of the T2IFLC [6]. In this way, determining the scientific structure of a T2IFLC in the system of the nonlinear control may be an effective approach to look at it [7,8]. However, the orderly outline and strength examination of the T2IFLC are yet difficult issues because of its generally more intricate structure [9,10]. Conventional PID is not able to give general solution to all control problems because the processes involved are in general complex and with delays, nonlinear, timevariant, non-stationary, and often with poorly defined dynamic. To overcome these difficulties, various types of modified fuzzy controllers are developed. In [12,13] T2IFPID controller and Popov Lyapunov method for stability analysis is presented which gives better performance as compare to traditional prop-integ-deriv controller.

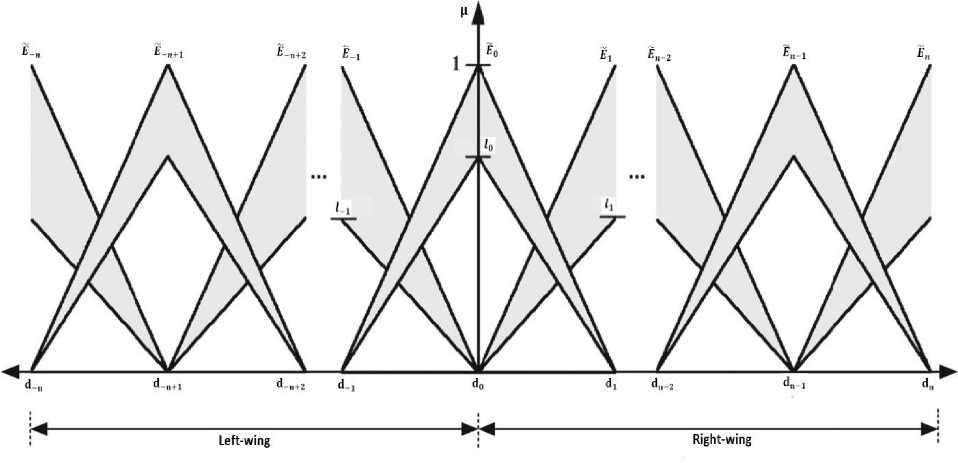
Fig.1. Demonstration of Type-2 Interval triangular membership function for error

In this segment, the proposed T2IFLC structures inputoutput mapping is determined. For effortlessness, the antecedent part for the T2IFLC FM of the fuzzy rule base is presented by consistently conveyed symmetrical triangular. From the error (e) i.e. the linguistic value of the input are indicated as Ё / where i = {-n, (-n+1) ,(-n+2), . . . , -2, -1, 0, 1, 2, . . . ,(n-2), (n-1), n}. The presented type-2 fuzzy set (Ё / )  is referred as LMF

(цЁ / ) and UMF^E / ). As appeared in Fig.1, the height of the LMF is represented by l_n though the center of the Ё / is indicated by d_n. The input T2IFSs are symmetrical, subsequently, the information space (e) is separated in two fundamental districts which are named as the Left wing (e £ [cL_n d₀]) and Right wing (e £ [d₀ d_n]). In addition, following properties are controlled by an additional type reduction system since T2IFLC utilize and process T2IFSs. A few investigations have been introduced to examine the impact of the footprint of uncertainty and additional type reduction process on wanted fuzzy enrolment (i.e., control surface) [5]. The type-2 interval fuzzy mapping [4], characterized T2IFLC membership functions:

(i) цЁ / (e) + цЁ /+1 (в) = 1, i = -n,. ,-2,-1, 0, 1,2,. .,n (ii) цЁ / (б) = l / * цЁ / (e), -n,. ,-2,-1, 0, 1,2,. .,n

(iii) l - = l_/, i = 1,2,3,. . . ,n

The proposed T2IFLC run development is described as:

r / : IF (e) is Ё THEN (e^) is 5 / , i = 1,2,.....,N (1)

The aggregate total sum of rule numbers is given as N = 2n + 1, while the resultant part deciphers the crisp singleton esteems ( 5 / ) which are consistently disseminated in the scope of [-1, 1]. Liang and Mendel revealed that the defuzzified output of a T2IFLC can be computed as:

^e /uz

-^Z /uz ⁺ -^r /uz

where (e ^r ' f _Uz) and (e^z' ^ _Mz) projects the endpoints of the type deduced set.

Moreover (er'^,uz), (ez ) are calculated as below:

_r,   ₌ 1 /=1^ (-»В^ = _£ +₂^^

- juz  S^^-)^® (-)

ez'      :

— j uz

_ ^ ^=1 ЦЕ₁(е)*В₁+^^_к+ 1 ЦЁ₁ ( e ) *B j

■      2 ;=1 Sj? i ( e ) +2 7= _R+ 1 ME i ( — )

Here, (R, L) is the emerging set that decreases/ increases separately. T2IFLC completely covers the triangular T2IFSs in the feeling of upper and lower FM’s. Subsequently, it can be constantly ensured that a crisp estimation of e has a place with two progressive T2IFSs, i.e. Ё / and E / ₊₁. Subsequently, for any crisp information, simply two rules (N = 2) are constantly operated as the points (R, L) are constantly equivalent to "1". A triangular shape FM of T2IFLC is obtained in the form of LMF and UMF. The reduced type set are determined as:

e^r '

el'

— fuz

дЕ г ( б ) *В_г + д Е + ( e ) *B₁₊₁

fuz

^д.^Е i (e) + д Ё₁₊₁ ( e )

д E_t (e)*B j + #i£₁₊₁ ( e ) *B₁₊₁

Д E_t ( e ) + д£ ;+1 ( е )

After replacing (5) in (2), proposed T2IFLC closed form mapping is obtained. Following are the properties of the presented a T2IFLC output.

• (i)    In relation to ‘e’, ‘e' f _uz’ has a continual function.

• (ii)    In relation to the input ‘e’, ‘e' f _uz’ is proportional, i.e. 6 fuz (^e) = -^e fuz ( ^-e ).

• (iii)    In an event that if an input error equivalent to zero then fuzzified error equivalents to be zero. It is mandatory to have zero error i.e.  (e) = 0 then

^e_fuz ~ ⁰

• III.    Design Strategy For T2ifpid Controller

In this section, the outlined procedure for singular input T2IFLC is presented. The output is expressed in the error (e) domain since the T2IFLC has singular input. This clarifies the design method of T2IFLC to the generation of non-linear control curve. In this strategy, the height (l_;) of lower-side FM’s of E ^ are considered as design parameters. Firstly, design parameters effect on T2IFLC are scrutinised and then an autonomous design method is proposed to generated control curves/curves. The parameters for T2IFLC structure are set as B_-1 = —1, B₊₁ = +1, B o = 0, d_-1= -1, d₊₁ = +1 and d₀ = 0 [11]. For the information Left-wing (e £ [—1, 0]), the end purposes of the type decreased set would then be able to be inferred as takes after:

l'    _    -дЕ-1(е)

— fuz   дЕ-1(е) + цЕо(е) ’ r'     _ — дЕ-1(e)

— ^fuz   цЕ -1 (е) + ДЕ д (е )

For the Right-wing (e £ [0, +1]), the end point of the type deduced sets reduces to:

_l,     _      цЕ 1 ( б )

- ^fuz ~ ДЕ с ( б) + дЕ 1 ( б ) ’

^Д Е 1 ( 6 )

e , = _ -———

- ^fuz   цЕ о ( в ) + дЕ 1 ( в)

Table 1. Expressions of £^l^_Mz and e^T

	Left wing ‘e’ £ [—1 , 0]	Right wing ‘e’ £ [0 , +1]
e l'	-ДЕ 1 ! £ )	цЕ 1 (e)
— fuz	ДЕ -1 ( в) + цЕ о ( в )	дЕ о ( e) + цЕ 1 ( e )
er'_	-ДЕ -1 ( e )	цЕ 1 ( e )
	цЕ -1 ( e ) + дЕ о ( e)	дЕ о ( e ) + дЕ 1 ( e)

To inspect the impact of the design parameters ( l_-1 , l₀ , l₁ ) on the output effectively the inferred explanatory articulations of e^l' f _uz and e^r' ^ for a

"three rule" interval T2IFLC are organized in Table 1. In this examination, the just Right-wing will be assessed in detail. Because of symmetrical and uniformly distributed nature of input and output FM, the evaluation of Rightwing can be extended for Left-wing in detail. The accompanying meta-rules inferred to shape a control activity from the determined articulations of e¹' and —^Г'fun for Right-wing, to get a palatable framework execution.

• a.    The values of ‘ e^l' f _uz ’ decrements/increments, if the values of ^.E₁(e) (i.e.l₁) decrements/increments respectively.

• b.    The values of  ‘e^r' f _uz ‘ increments/decrements, if

the     values     of ЦЕ0(е)     (i.e.

• c.    If the values of ‘l1 ’ is incremented while ‘l0 ’ is decremented then the values of   ‘ e^fuz ‘is

incremented since the values of both ‘er'uz’ and ‘ el'fuz ‘ are incremented. Hence, we obtainan aggressive control action.

• d.    If the values of ’l1’ is decremented while ‘l0’is

incremented then the values of ‘ e^fuz ‘is decremented since the values of both ‘er'uz’ and ‘ -'^ ‘ are decremented. Hence, we obtain a smooth control action.

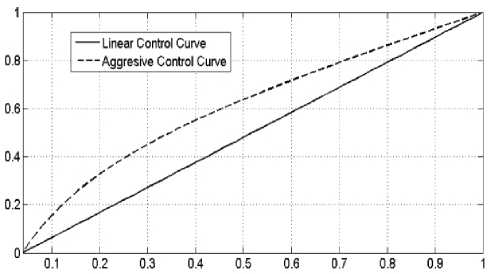
By choosing l1 moderately greater then l0, a forceful nonlinear control activity can be produced i.e.1

^{— l} 1 = ^l -1 — ^l 0 — 0. To get aggressive control curve, selecting m₁ = m_-1 = 0.9 and m₀ = 0.2 , the control curve showed in Fig.2. At the point when e is near zero, the control curve has a high affect ability. For quick transient framework response, aggressive control curve is favoured. At set point value, i.e. e equals to zero aggressive control action is sensitive to noises.

Smooth control action is acquired by choosing l0 moderately greater than l1, i.e. 1 — l0 — l1= l-1 — 0. To acquire smooth control curve given in Fig. 3, selecting l1= l-1 = 0.2 and l0 = 0.9. At the point when e is near to zero, it has low affectability. For robust control performance against parameter vulnerabilities and additionally background noises, smooth control curve is favoured.

The secondary part of proposed controller structure is a traditional prop-integ-deriv controller. The control law for T2IFPID controller is given by

^u(t) = ^K P ⁽06 fuz ⁽0 ^{+ K(}0 J 6 fuz ⁽0 + ^kd  ^    ⁽8)

where,

K_P = Proportional gain

K_D = Derivative gain

K = Integral gain

where

Fig.2. Linear control curve versus Aggressive control curve

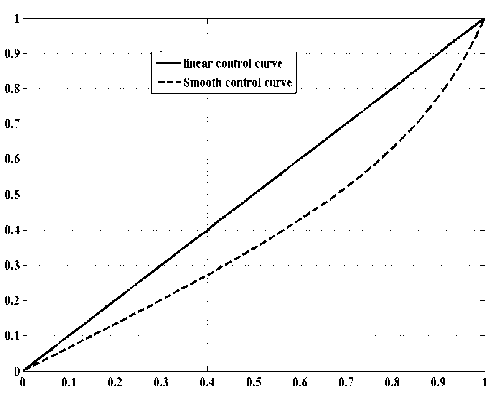
Fig.3. Linear control curve versus Smooth control curve

• IV.    Stability Analysis

Robust Stability Analysis for fuzzy based systems is carried out through Popov-Lyapunov method [13]. In this approach initially, expand a nonlinear system into a Taylor series. As presented in [13] the system is described in terms of Perturbed Lur’e system. Following are the steps to determine the robust stability.

A_r—A-- b v^T, Q_T—cE + —, R_T — - —

• -^Г       y     —        Y , -^Г       Y

• 4.    Choose a positive-definite matrix ‘E₀ ’ such that cE= cE₀ + SI, then the proper value of ‘5’ can be obtained.

• 5.   ‘ P ’ i.e. measurement of robustness can be

obtained can be obtained from inequality [13].

• V.    Simulation Result And Stability Analysis

0.12e ^-2^s

For calculating transfer function of CSTR cooling process, the step response is taken into consideration. For the step response, the input is step input, the initial temperature is taken as 57 ° C and the set point is taken as 45 ° C. The process has very large dead time and is highly damped. Therefore, the step response can be fitted into a simple first-order model with dead-time.

Therefore, the transfer function of the CSTR process is given by

G(s) —

3s+1

Tuning of prop-integ-deriv for CSTR is done by Ciancone correlation [12], it is resulting as follows: K_p =6.667, K_D — 2 and K ] — 1 .9. Simulation result of CSTR is shown in fig.4 has comparison between T2IFPID with aggressive, smooth control action and PID controller. Initially unit step input is applied to the process. It can be seen in Fig. 4 and Fig. 5, three different types of controller are able to track the reference with different rise time and settling time. Response due to Aggressive control action Fuzzy controller has less rise time compared to other controller; while response due to Smoother control action Fuzzy controller has higher settling time compared to other controller performance. Table 2 shows step response characteristics of prop-integ-deriv controller, T2IFPID controller (Smooth) and T2IFID controller (Aggressive); where unit step input is applied to the process.

To find out the stability of fuzzy system using Popov-Lyapunov method first system is converted into perturbed Lur’e system [13], which is represented by transfer function as follows-

-0.1067S+0.32

G^_{py (s) —  _

—s ]T2       S2+1.269S+0.525

-0.1067S+0.32

G д_1Т7(з) —  9           _(15)

_- и 2 4 7    S2 + 1.226S+0.653

ArP + PA_r - PR_r + Q_r — 0     (12)

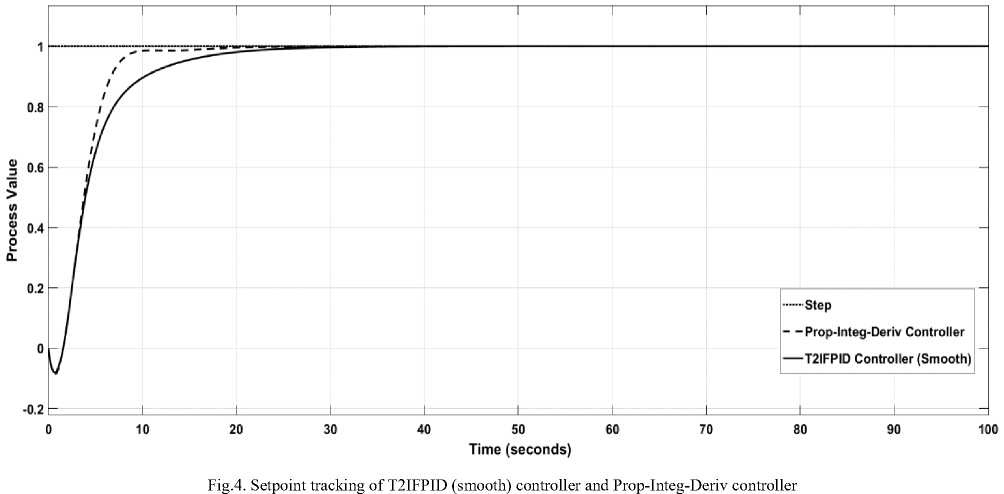
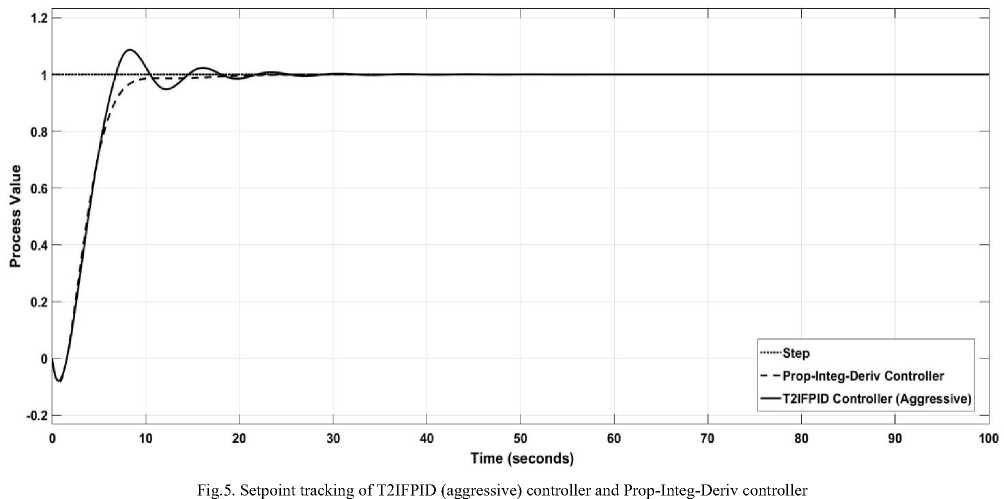
Table.2. Step response characteristic of continuous stirred tank reactor with the controller

	Prop-Integ-Deriv controller	T2IFPID controller (Smooth)	T2IPID controller (Aggressive)
Rise Time(sec.)	4.540	7.913	4.195
Settling Time(sec.)	42.273	32.668	36.972
Overshoot (%)	0.000	0.502	8.152
IAE	4.386	5.488	4.585

popov plot of the system represented by transfer function (14), from that plot it can be concluded as given system satisfies popov criterion for slope of line r > 1.45 . Similarly, popov plot, of system represented by (15) is shown in Fig. 7, from that it can be seen that given system satisfies popov criterion for slope of line r > 1.44. Appling Lyapunov stability method P matrices are given as follows-;

E s-1T2

1.4766

[-0.1342

-0.1342"

0.4102 -

Transfer function G_s-1T 2 (s') represent perturbed Lur’e system of fuzzy system which implement smoother control action while Transfer function (i_A-1T2(s') represent perturbed Lur’e system of fuzzy system which implement aggressive control action. Fig. 6 represent

1.3204   -0.3408

[-0.3486   0.2845 .

Given P matrices are symmetric positive-definite, from this popov criterion and Lyapunov stability method its can be concluded that equilibrium point zero is uniformly asymptotically stable. Robustness measure /? can be calculated using [13], which are 0S-1T2 = 0.7015 for smoother control action fuzzy system and PA-1T2 = 0.4627 for aggressive control action fuzzy system. From this it is stated that smoother control action fuzzy system is more robust than aggressive control action fuzzy system.

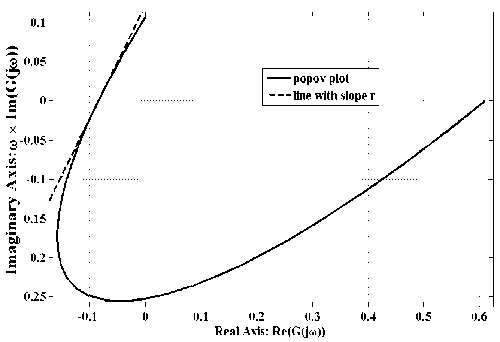
Fig.6 Popov plot of G S-iTz (s)

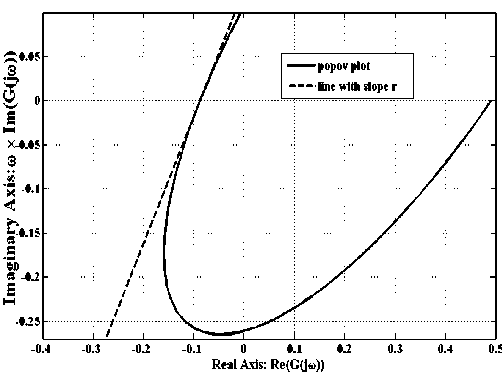
Fig.7 Popov plot of G_A- i _T2(s)

• VI.    Conclusion

The proposed design method is the simplest method to design T2IFLC. The proposed controller possesses the properties of Prop-Integ-Deriv controller. The T2IFLC controller output is completely expressed in error. Hence, an autonomous design method is proposed to generate nonlinear control curves. The performance of the T2IFLC is compared with different controllers to investigate transient state performance and disturbance rejection.

Stability analysis is carried through Popov-Lyapunov method to define the robustness of the proposed controller.

Aggressive control action is favored for quick transient reaction since it is delicate to the commotion, particularly around setpoint esteem. At relentless state, controller, which has a smooth control surface, is conceivably more powerful against non-linearity and vulnerabilities. T2IFLC gives a diverse reaction to the various footprint of uncertainty parameters. T2IFPID controller beats the prop–integ–deriv controller.

• [1]    KJ Åström, T Hägglund, The future of PID control , Control Engg. Practice 9 (11) (2001) 1163–1175.

• [2]    KJ Åström, T Hägglund, PID controllers: Theory, Design and Tuning , Instrument Soc. of America, Research Triangle Park, NC, 1995.

• [3]    G. Mann, Bao-Gang Hu, R. Gosine, “Analysis of direct action fuzzy PID controller structures,” IEEE Trans. on Syst., vol. 29, no. 3, pp. 371-388, Jun.1999.

• [4]    D. Wu, “On the fundamental differences between interval type-2 and type-1 fuzzy logic controllers,” IEEE Trans. on Fuzzy Syst., vol. 20, no. 5, pp. 832-848, Oct. 2012.

• [5]    O. Castillo, R. Martinez-Marroquin, P. Melin, F. Valdez, J. Soria, “Comparative study of bio-inspired algorithms applied to the optimization of type-1 and type-2 fuzzy controllers for an autonomous mobile robot,” Info Sciences, vol. 192, pp. 19-38, June 2012.

• [6]    X. Du and H. Ying, “Derivation and analysis of the analytical structures of the interval type-2 fuzzy-PI and PD controllers,” IEEE Trans. on Fuzzy Syst., vol. 18, no. 4, pp. 802-814, Aug. 2010.

• [7]    M. Nie and W. Tan, “Analytical structure and characteristics of symmetric Karnik-Mendel type-reduced interval type-2 fuzzy PI and PD controllers.” IEEE Trans. on Fuzzy Syst., vol. 20, no. 3, pp. 416-430, June 2012.

• [8]    H. Zhou and H. Ying, “A method for deriving the analytical structure of a broad class of typical interval type-2 mamdani fuzzy systems,” IEEE Trans. on Fuzzy Syst., vol. 21, no. 3, pp. 447-458, June 2013.

• [9]    M. Biglarbegian, W. Melek and J. Mendel, “On the stability of interval type-2 TSK fuzzy logic control systems,” IEEE Trans. on Fuzzy Syst., vol. 40, no. 3, pp. 798-818, June 2010.

• [10]    H. Lam and L. Seneviratne, “Stability analysis of interval type-2 fuzzy-model-based-control systems,” IEEE Trans. on Syst., Man, and Cybernetics, Part B (Cybernetics), vol. 38, no. 3, pp. 617-628, June 2008.

• [11]    T. Kumbasar, “A simple design method of interval type-2 fuzzy PID controllers,” Soft Comput., vol. 18, no. 7, pp. 1293-1304, 2014.

• [12]    T. Marlin, “Process control designing processes and control systems for dynamic performance,” ch. 9, pp. 279281.

• [13]    T. Kumbasar, “Robust stability analysis of PD type single input interval type-2 fuzzy control systems,” Int. Conf. on Fuzzy Systems, July 2014.

  Authors’ Profiles

  
  
  

  Tejas D. Gangurde completed Master of Technology in Electrical Control Systems from Walchand College of Engineering, Sangli, India-416415. Completed Bachelor of Electrical Engineering from University of Pune in 2014.

Vrushali P. Mahajan currently pursuing Master of Technology in Electrical Control Systems from Walchand College of Engineering, Sangli, India-416415.