Design Sliding Mode Modified Fuzzy Linear Controller with Application to Flexible Robot Manipulator
Автор: Mahdi Mirshekaran, Farzin Piltan, Zahra Esmaeili, Tannaz Khajeaian, Meysam Kazeminasab
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 10 vol.5, 2013 года.
Бесплатный доступ
This paper studies the use of Modified Proportional-Integral-Derivative Sliding Mode Controller (MPIDSMC) control used to control a flexible manipulator. The control gain in the MPIDSMC controller has been determined in an empirical way so far. It is a considerable time-consuming process because the control performance depends not only on the control gain but also on the other parameters such as the payload, references and PID joint servo gains. Hence, the control gain must be tuned considering the other parameters. In order to find the optimal control gain for the MPIDSMC controller, a fuzzy logic approach is proposed in this paper. The proposed fuzzy logic scheme finds an optimum control gain that minimizes the tip vibration for the end effector of the flexible manipulator. Tuned gain response results are compared to results for other types of gains. The effectiveness of using the fuzzy logic appears in the reduction of the computational time and the ability to tune the gain with different loading condition and input parameters.
Modified PID Controller, Flexible manipulator, sliding mode controller, vibration of end effector, fuzzy logic theory
Короткий адрес: https://sciup.org/15014595
IDR: 15014595
Текст научной статьи Design Sliding Mode Modified Fuzzy Linear Controller with Application to Flexible Robot Manipulator
Email: ;
The flexible manipulator started to play an important part in many engineering applications nowadays. Major advantages of flexible manipulators include small mass, fast motion, and large force to mass ratio, which are reflected directly in the reduced energy consumption, increased productivity, and enhanced payload capacity. Unlike the rigid manipulators, the difficulties facing the usage of flexible manipulators are numerous. The modeling of the flexibility of the manipulator is one of the challenges, the non-minimum phase problem, which appears from the modeling of the flexible manipulators, is also another challenge. The precise and availability of the measured variables used in the control is the third challenge. The control of flexible manipulators has been studied with great interest by many researchers over the past years due to its pronounced benefits. To find a controller that can achieve the end effector position of the flexible manipulator in a short time in addition to a suppression of its vibration to be able to achieve the tasks is the main goal of the control of flexible manipulator in the free space. Although significant progresses have been made in many aspects over the last two decades, many issues are not yet resolved yet, and simple, effective, and reliable controls of flexible manipulators remain open requests [1-15].
There are several methods for controlling a flexible robot manipulator, which all of them follow important main goals, namely, acceptable performance [16-21]. However, the mechanical design of flexible robot manipulator is very important to select the best controller to have a reduce vibration but in general two types schemes can be presented, namely, a joint space control schemes and an operation space control schemes[13-23]. One of the simplest ways to analysis control of multiple Degrees Of Freedom (DOF) flexible robot manipulator is analyzed each joint separately such as SISO systems and design an independent joint controller for each joint. In this methodology, the coupling effects between the joints are modeled as disturbance inputs. To make this controller, the inputs are modeled as: total velocity/displacement and disturbance. Design a controller with the same formulation and different coefficient, low cost hardware and simple structure controller are some of most important independent-joint space controller advantages. In the absence of robot knowledge, proportional-integral-derivative (PID) may be the best controller, because it is model-free, and its parameters can be adjusted easily and separately [24-36]. And it is the most used in flexible robot manipulators. In order to remove steady-state error caused by uncertainties and noise, the integrator gain has to be increased. This leads to worse transient performance, even destroys the stability. The integrator in a PID controller also reduces the bandwidth of the closed-loop system. PD control guarantees stability only when the PD gains tend to infinity, the tracking error does not tend to zero when friction and gravity forces are included in the flexible robot manipulator dynamics [38-69]. Modelbased compensation for PD control is an alternative method to substitute PID control [10-28], such as adaptive gravity compensation [11-33], desired gravity compensation [16-49], and PD+ with position measurement [18-69]. They all needed structure information of the robot gravity. Some nonlinear PD controllers can also achieve asymptotic stability, for example PD control with time-varying gains [5], PD control with nonlinear gains [6], and PD control with feedback linearization compensation [8]. But these controllers are complex; many good properties of the linear PID control do not exist because these controllers do not have the same form as the industrial PID. Nonlinear controllers divided into six groups, namely, feedback linearization (computed-torque control), passivity-based control, sliding mode control (variable structure control), artificial intelligence control, Lyapunov-based control and adaptive control[10-69]. Sliding mode controller (SMC) is a powerful nonlinear controller which has been analyzed by many researchers especially in recent years. This theory was first proposed in the early 1950 by Emelyanov and several co-workers and has been extensively developed since then with the invention of high speed control devices [12]. The main reason to opt for this controller is its acceptable control performance in wide range and solves two most important challenging topics in control which names, stability and robustness [7, 17-48]. Sliding mode control theory for control of flexible robot manipulator was first proposed in 1978 by Young to solve the set point problem ( q^ = 0) by discontinuous method in the following form;
т = (T + (q, t) if S i >0 (1)
(q,t) lт - (q, t) if S i <0
where S1 is sliding surface (switching surface), 1 = 1,2,......, n for n -DOF flexible robot manipulator, t1 (q, t)
is the 1th torque of joint. In recent years, artificial intelligence theory has been used in sliding mode control systems. Neural network, fuzzy logic and neuro-fuzzy are synergically combined with nonlinear classical controller and used in nonlinear, time variant and uncertain plant (e.g., robot manipulator). Fuzzy logic controller (FLC) is one of the most important applications of fuzzy logic theory. This controller can be used to control nonlinear, uncertain, and noisy systems. This method is free of some model techniques as in model-based controllers. As mentioned that fuzzy logic application is not only limited to the modeling of nonlinear systems [31-45] but also this method can help engineers to design a model-free controller. Control robot arm manipulators using modelbased controllers are based on manipulator dynamic model. These controllers often have many problems for modeling. Conventional controllers require accurate information of dynamic model of robot manipulator, but most of time these models are MIMO, nonlinear and partly uncertain therefore calculate accurate dynamic model is complicated [32]. The main reasons to use fuzzy logic methodology are able to give approximate recommended solution for uncertain and also certain complicated systems to easy understanding and flexible. Fuzzy logic provides a method to design a model-free controller for nonlinear plant with a set of IF-THEN rules [22-69]. Normal combinations of fuzzy logic methodology (FLM) and modified PID sliding mode controller (MPIDSMC) are to apply fuzzy parallel compensator at the same time [22-45], while FLM compensates the control error, MPIDSMC reduce the error of fuzzy inference system such that the final tracking error is asymptotically stable [12-38]. This paper is organized as follows; second part focuses on the modeling dynamic formulation based on Lagrange methodology, fuzzy logic methodology and computed torque controller to have a robust control. Third part is focused on the methodology which can be used to reduce the error, increase the performance quality and increase the robustness and stability. Simulation result and discussion is illustrated in forth part which based on trajectory following and disturbance rejection. The last part focuses on the conclusion and compare between this method and the other ones.
II . THEORY
Dynamic Formulation of Flexible Robot Manipulator: It can be evinced from the force expressions that the total input forces acting on each module can be resolved into an additive component along the direction of extension and a subtractive component that results in a torque. For the first module, there is an additional torque produced by forces in the third module.
The model resulting from the application of Lagrange’s equations of motion obtained for this system can be represented in the form
F coeff I = ° (9) 9 + с(я)9 + 6(9) (2)
where т is a vector of input forces and q is a vector of generalized co-ordinates. The force coefficient matrix F coeff transforms the input forces to the generalized forces and torques in the system. The inertia matrix, D is composed of four block matrices. The block matrices that correspond to pure linear accelerations and pure angular accelerations in the system (on the top left and on the bottom right) are symmetric. The matrix C contains coefficients of the first order derivatives of the generalized co-ordinates. Since the system is nonlinear, many elements of C contain first order derivatives of the generalized co-ordinates. The remaining terms in the dynamic equations resulting from gravitational potential energies and spring energies are collected in the matrix G. The coefficient matrices of the dynamic equations are given below [46-55],
G (9) = (6)
—m1g — m2g + кц^ + (1/2)6 1 -s01)+ k21(s1 - (1/2)6 1 - s01) - m3g
-m2gcos(6 i ) + ^(s + (1/2)6 2 - 502) + k22(s2 - (1/2)6 2 - s 02 ) —т2дсоз(в1)
—m3gcos(6 1 + 6 2 ) + & 1з (5 з + (1/2)6 з - s0 3 ) + k 23 (s 3 - (1/2)6 з - s0 3 )
т з Я з датСе у ) + m з s з gsln(0 1 + e2) + т з 32дзт(е1) + kn(s 1 + (Х^^ - s 01 )(1/2) +ft 21 (S 1 - (1/2)6 1 -S 01 )(-1/2)
т з 5 з д51п(6 1 + 6 2 ) + k 1 2(s2 + (l/2)62- S o2 )(1/2) + k22(s2 - (l/2)62- S o2 )(-1/2)
к 1з (5 з + (1/2)6 3 - S 03 )(1/2) + Ms3 - (1/2)6 3 - $ оз )(-1/2)
Design PID Controller: Design of a linear methodology to control of flexible robot manipulator was very straight forward. Since there was an output from the torque model, this means that there would be two inputs into the PID controller. Similarly, the outputs of the controller result from the two control inputs of the torque signal. In a typical PID method, the controller corrects the error between the desired input value and the measured value. Since the actual position is the measured signal. Figure 1 is shown linear PID methodology, applied to flexible robot manipulator [56-69].
e(t) = 6a(t) - 6d(t) (7)
Fcoeff =
|
1 |
1 |
cos(6 1 ) |
cos(6 1 ) |
cos(6 1 + 6 2 ) |
cos(6 1 + 6 2 ) |
|
0 |
0 |
1 |
1 |
cos(6 2 ) |
cos(6 2 ) |
|
0 |
0 |
0 |
0 |
1 |
1 |
|
1/2 |
-1/2 |
1/2 |
-1/2 |
1/2+ S 2 Sin(6 2 ) |
-1/2 + S 2 Sin(6 2 ) |
|
0 |
0 |
1/2 |
-1/2 |
1/2 |
-1/2 |
|
. 0 |
0 |
0 |
0 |
1/2 |
-1/2 |
° (9) = mi + mz + тз
UP1D = K „ a e + KVae + K^e
mzcos(91)
+ m3cos(91)
m3cos(9i + 9z)
-n^sr^ty
— mзSzSin(91')
-
— mзSзSin(91 + 9z)
-
— mзSзSin(91 + 9z)
nizcos(91) + ni3cos(9i)
mz + m3
Пз cos(9z)
-m3S3Sin(9z)
-Пз5з sin(9z)
— mzSzSin(91)
m3cos(9i + 9z) -n^SzSin^i) —mзSзSin(91 + 9z)
-тз5з5<п(91 + 9z)
|
m3cos(9z) |
- m3S3Sin(9z) |
-m3S3Sin(9z) |
0 |
|
m3 |
m 3S3Sin(9z) |
0 |
0 |
|
m3SzSin(9z) |
mzSZ + 1 + fz + 1з + m3sZ + m3sZ + Zm3S3cos(9z)Sz |
fz + m3SZ + f3 + m3S3 cos(9z)sz |
1з |
|
0 |
1z + m3SZ + I3 |
fz + m3SZ + f3 |
1 |
|
+ m3S3cos(9z)Sz1 |
f3 |
||
|
0 |
1з |
1з |
1з- |
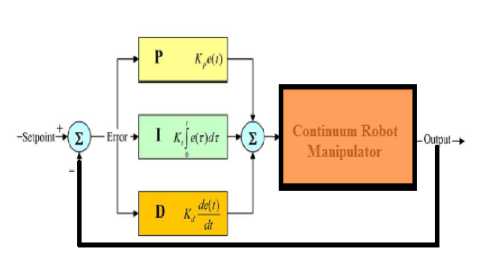
Fig 1: Block diagram of linear PID method
cQO =
|
c11 + c21 |
- 27nzsin(91)91 - 2т.зsm(9])9] |
-2т.зsm(9] + 62) (9, + 92) |
—mzsz cos(91)(91) +(1/2)(c„+ c21) -тз.2 cos(91)(91) -тз.з cos(61 + 9z)(91) |
—т.зSзS;n(91 + 92) 0 |
|
|
0 |
c12 + c22 |
- 2тз sm(9z) (6 + 62) |
-тз.?з(91) +(1/2) (c12 + ^2) —тзSz(61) -тз.з cos^X^) |
- 2тз. cos(92)(91) -тз.з cos(9z)(9z) |
0 |
|
0 |
2т.зsm(9z)(91) |
c13 + c23 |
-тз^. cos(9z)(91) -тз.з^Х |
- 2rn3s3(61) —тзsз(9z) |
(1/2) (c13 + c23 |
|
(1/2) (c11 + c21- |
2rn3S3cos(9z)(9,) - 2rn3sz(e,) + 2тzSz(9,) |
2rn3S3(9]+ ty -2т.зSzCOs(9z) (6! + 62) |
2тз.з.?2 .т(92)(92) +(12/4) (c11 + ^1) |
m3s3s2 sm(9z)(9z) |
0 |
|
0 |
(1/2)(c,z + c22) + 2тзSзCOS(9z)(61) |
2тз.$з (61 + 62) |
тз.з.2 .т(92)(91) |
(12/4) (c12 + ^2) |
0 |
|
0 |
0 |
(1/2)(c13 - c23) |
0 |
0 |
(12/4) (c13 + c23 |
The model-free control strategy is based on the assumption that the joints of the manipulators are all independent and the system can be decoupled into a group of single-axis control systems [18-23]. Therefore, the kinematic control method always results in a group of individual controllers, each for an active joint of the manipulator. With the independent joint assumption, no a priori knowledge of robot manipulator dynamics is needed in the kinematic controller design, so the complex computation of its dynamics can be avoided and the controller design can be greatly simplified. This is suitable for real-time control applications when powerful processors, which can execute complex algorithms rapidly, are not accessible. However, since joints coupling is neglected, control performance degrades as operating speed increases and a manipulator controlled in this way is only appropriate for relatively slow motion [44, 46]. The fast motion requirement results in even higher dynamic coupling between the various robot joints,
which cannot be compensated for by a standard robot controller such as PID [50], and hence model-based control becomes the alternative.
Sliding mode controller: Consider a nonlinear single input dynamic system is defined by [6]:
Х(П ) — f (x) + b(x)lt (9)
Where u is the vector of control input, x(n) is the nth derivation of x , x = [x, Х, Х , ..., x(n - 1)]r is the state vector, f (x) is unknown or uncertainty, and b(x) is of known sign function. The main goal to design this controller is train to the desired state; x ^ = [xd,xd,xd,...,xd(n - 1)]r , and trucking error vector is defined by [6]:
x = x - xd — [x,..., x(n i:i]r (10)
A time-varying sliding surface s(x, t) in the state space Rn is given by [6]:
d „
s(x, t) = (— + A)n 1 x — 0
where λ is the positive constant. To further penalize tracking error, integral part can be used in sliding surface part as follows [6]:
s(x, t) — (^ + Л) ” 1 ^J xdt) — 0
The main target in this methodology is kept the sliding surface slope s(x, t) near to the zero. Therefore, one of the common strategies is to find input U outside of s(x, t) [6].
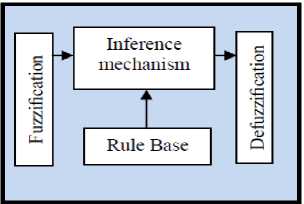
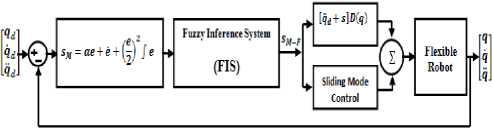
I"dts2(x, t) < — If S(0)>0^^S(t) <-< To eliminate the derivative term, it is used an integral term from t=0 to t=treach Гt—treach d / ft—treach ~ Jt=0 dfts(t) <-Jt—0 ^ S (trench) — S(0) < -<(treQCh - 0) Where treac^ is the time that trajectories reach to the sliding surface so, suppose S(treac^ = 0) defined as; 0-S(0) <-4(treach) ^ treach< ^ And if S(0) < 0 ^ 0 - 5(0) < -4(treach) ^ (17) S(0)< -^(treach) ^ treach< ^"1)1 Equation (17) guarantees time to reach the sliding surface is smaller than |S^0)I since the trajectories are outside of 5(t). if Streach — S(0) ^ error(x - xd) — 0 suppose S is defined as s(x, t) = (dt + A) x — (x - xd) + A(x - Xd) The derivation of S, namely, 5 can be calculated as the following; S — (X - Xd) + A(X - Xd) suppose the second order system is defined as; x — f + n ^ S — f + U — xd(21) + A(X - Xd) Where f is the dynamic uncertain, and also since 5 = 0 and 5 — 0, to have the best approximation ,U is defined as U — -f + xd - A(X - Xd) A simple solution to get the sliding condition when the dynamic parameters have uncertainty is the switching control law [52-53]: Udis — U- K(x, t) • sgn(s) where the switching function sgn(S) is defined as [1, 6] ( 1 s > 0 sgn(s) — |-1s <0 (0s — 0 and the K(x, t) is the positive constant. Suppose by (25) the following equation can be written as, Idts2(x, t) — S^S — [f - f - Ksgn(s)] • S — (f-f)^S-K|S| and if the equation (17) instead of (16) the sliding surface can be calculated as s(x, t) — (dt + я)2 (j()Xdt) — (X-XdH 22(X - Xd) -A2(x - Xd) in this method the approximation of U is computed as [6] U — -f + xd - 22(X - Xd) + A2 (x - Xd) Based on above discussion, the sliding mode control law for multi degrees of freedom robot manipulator is written as [1, 6]: T Teq + Tdis Where, the model-based component Teq is the nominal dynamics of systems calculated as follows [1]: Teq = [D-1 (f + C + G) + S]D and Tdis is computed as [1]; Tdis = К • sgn(S) By (30) and (29) the sliding mode control of robot manipulator is calculated as; t = [D-1(f + C + G) + S]D + К • sgn(S) Proof of Stability: The lyapunov formulation can be written as follows, V = |st. D. S the derivation of V can be determined as, V = |st. D. S + ST DS the dynamic equation of robot manipulator can be written based on the sliding surface as MS = -VS + DS + f + C + G it is assumed that ST(D-lf + C + G)S = 0 by substituting (34) in (35) V = lSTDS-STf + CS + St(dS + f + CS + G) = St(dS + f + CS + G) suppose the control input is written as follows U = G^^ear + + = [D-1 (f + C + G) + S]D + К. sgn(S) + D + CS + G by replacing the equation (40) in (32) V = ST(DS + f + C + G-DS-f+CS + G — Ksgn(S) = ST(dS + f + CS + G - Ksgn(S)) and IDS' + f + CS + G| < |DST| + |f + CS + G| (39) the Lemma equation in robot arm system can be written as follows K„ = [|D^| + |f + CS + G| + q]i, i = (40) 1, l, 3,4,^ and finally; n ^< -^^i ISil i=1 Figure 2 show the pure PID sliding mode controller applied to flexible robot. Fig 2: Sliding Mode Controller Fuzzy Logic Technique: Based on foundation of fuzzy logic methodology; fuzzy logic management has played important rule to design nonlinear management for nonlinear and uncertain systems [16-36]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of;Input fuzzification (binary-to-fuzzy [B/F] conversion), Fuzzy rule base (knowledge base), Inference engine and Output defuzzification (fuzzy-to-binary [F/B] conversion). Figure 3 shows the fuzzy controller part. The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy managements to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno uses a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base [22-33] if xis A and у is В then z is C 'mamdani' if xis A and у is В then z is f (x, у)'sugeno' When x and у have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation (AND/OR ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method (COG) and Centre of area method (COA) are two most common defuzzification methods [34-69]. Where, the model-based component Teq is the nominal dynamics of systems and to position control of continuum robot manipulator Teq can be calculate as follows: Teq = |D 1 (f + C + G)+ S]D (46) and Tsat is computed as; Tsat = K • sat (s/0) И7) by replace the formulation (47) in (45) the control output can be written as; Fig 3: Fuzzy Controller Part III. METHODOLOGY Chattering phenomenon is one of the most important challenges in pure sliding mode controller with regards to the certain and partly uncertain systems. To reduce or eliminate the chattering in sliding mode controller most of researcher are focused on boundary layer method. In boundary layer method the basic idea is replaced the discontinuous method by saturation (linear) method with small neighborhood of the switching surface. B(t)_{x,\S(t)\< 0}; 0 >0 (42) where 0 is the boundary layer thickness. Therefore the saturation function Sat(S/0) is added to the control law as U = K(X, t) •Sat(s/0) where Sat (%) can be defined as ^(^ {1 —1 S/0 (S/0 > 1) (S/0 < -1) (-1< S/0<1) T = Teq + K. sat (^ (48) Г Teq + K. Sgn(S) ,\S\ > 0 = (Teq + K. S/0 ,\S\< 0 By (48) and (46) the sliding mode control of continuum robot manipulator is calculated as; T = [D—1(f + c + G)+ S]D + K (49) sat(5/0) To solve the challenge of pure sliding mode controller based on nonlinear dynamic formulation and chattering phenomenon this research is focused on applied modified PID fuzzy methodology to estimate the nonlinear equivalent formulation and reduce the chattering. In this method; modified PID sliding surface slope calculate and applied to fuzzy logic system to modified nonlinear sliding surface slope. Dynamic nonlinear equivalent part is estimate by performance/error-based fuzzy logic controller which applied to previous sliding surface slope. In fuzzy error-based sliding mode controller; error based Mamdani’s fuzzy inference system has considered with one input, one output and totally 7 rules to design nonlinear PID modified sliding surface slope. Figure 4 shows the modified PID fuzzy applied to sliding mode controller. ^modified—fuzzy [ae + e + ф2£в ] Z?_i0T<(x) Based on fuzzy logic methodology f (x) = Ufuzzy = Z?=i0r<(x) (51) where 9T is adjustable parameter (gain updating factor) and <(x) is defined by; Based on above discussion, the control law for multi degrees of freedom robot manipulator is written as: _ ZiM(xi)xj ZiM(xi) T = Teq + Tsat to Flexible Robot Manipulator Fig 4: Block Diagram of Fuzzy PID Modified New Sliding Mode Control
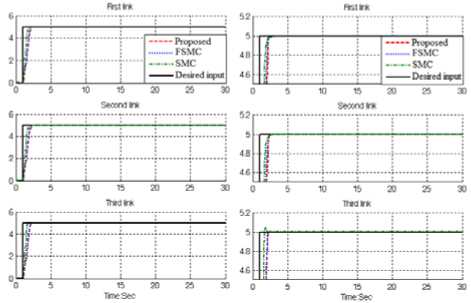
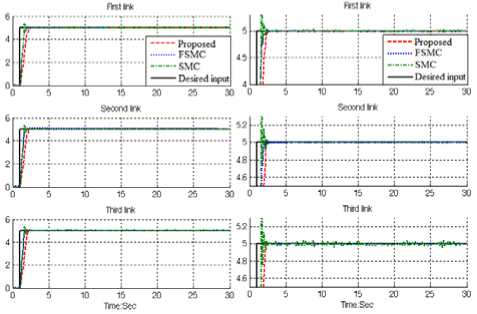
IV. RESULTS AND DISCUSSION In this section, we use a benchmark model, robot manipulator, to evaluate our control algorithms. We compare the following methods: PD sliding mode controller, conventional fuzzy sliding mode controller and fuzzy PID modified new sliding mode controller which is proposed method in this paper. The simulation was implemented based on MATLAB/SIMULINK. Close loop response of robot manipulator trajectory planning: Figure 5 illustrates the tracking performance in these methodologies. Fig 5: Pure SMC, Fuzzy SMC and Proposed method trajectory following without disturbance Based on Figure 5; pure SMC controller has a slight overshoot in all links, because this flexible robot is a highly nonlinear system and control of this system by pure nonlinear method is very difficult. Close loop response of trajectory planning in presence of disturbance: Figure 6 demonstrates the power disturbance elimination in these controllers in presence of disturbance for flexible robot manipulator. The disturbance rejection is used to test the robustness in this nonlinear system. Fig 6: Pure SMC, Fuzzy SMC and Proposed method trajectory following in presence of disturbance Based on Figure 6; by comparison between SMC, fuzzy SMC and proposed method, proposed methodology is more stable and robust than pure nonlinear controller.
V. CONCLUSION The important contributions of this paper are; design modified PID controller to pre adjust and tune the error, design fuzzy logic controller by one input and output to compensate nonlinear equivalent part in sliding mode controller and reduce the chattering phenomenon, partly linear term which is used to bypass the inertial term in nonlinear system and sliding mode controller which is a main nonlinear and robust controller. The structure of sliding mode controller with modified PID serial fuzzy inference compensator is new. We also propose parallel partly linear term structure compensator to reduce the error and increase the stability. ACKNOWLEDGMENT The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Research and Development Corporation Program of Iran under grant no. 2013-Persian Gulf-1A.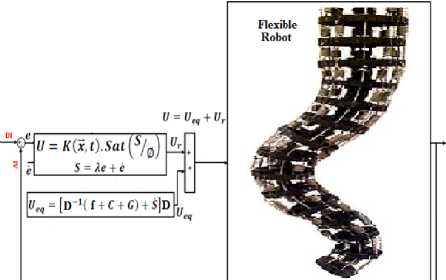
Список литературы Design Sliding Mode Modified Fuzzy Linear Controller with Application to Flexible Robot Manipulator
- G. Robinson, and J. Davies, “Continuum robots – a state of the art,”Proc. IEEE International Conference on Robotics and Automation, Detroit, MI, 1999, vol. 4, pp. 2849-2854.
- I.D. Walker, D. Dawson, T. Flash, F. Grasso, R. Hanlon, B. Hochner, W.M. Kier, C. Pagano,C.D. Rahn, Q. Zhang, “Continuum Robot Arms Inspired by Cephalopods, Proceedings SPIE Conference on Unmanned Ground Vehicle Technology VII, Orlando, FL, pp 303-314, 2005.
- K. Suzumori, S. Iikura, and H. Tanaka, “Development of Flexible Microactuator and it’s Applications to Robotic Mechanisms”, Proceedings IEEE International Conference on Robotics and Automation, Sacramento, California, pp. 1622-1627, 1991.
- D. Trivedi, C.D. Rahn, W.M. Kier, and I.D. Walker, “Soft Robotics: Biological Inspiration, State of the Art, and Future Research”, Applied Bionics and Biomechanics, 5(2), pp. 99-117, 2008.
- W. McMahan, M. Pritts, V. Chitrakaran, D. Dienno, M. Grissom, B. Jones, M. Csencsits, C.D. Rahn, D. Dawson, and I.D. Walker, “Field Trials and Testing of “OCTARM” Continuum Robots”, Proc. IEEE International Conference on Robotics and Automation, pp. 2336-2341, 2006.
- W. McMahan, I.D. Walker, “Octopus-Inspired Grasp Synergies for Continuum Manipulators”, Proc. IEEE International Conference on Robotics and Biomimetics, pp. 945- 950, 2009.
- I. Boiko, L. Fridman, A. Pisano and E. Usai, "Analysis of chattering in systems with second-order sliding modes," IEEE Transactions on Automatic Control, No. 11, vol. 52,pp. 2085-2102, 2007.
- J. Wang, A. Rad and P. Chan, "Indirect adaptive fuzzy sliding mode control: Part I: fuzzy switching," Fuzzy Sets and Systems, No. 1, vol. 122,pp. 21-30, 2001.
- M. Bazregar, Farzin Piltan, A. Nabaee and M.M. Ebrahimi, “Parallel Soft Computing Control Optimization Algorithm for Uncertainty Dynamic Systems”, International Journal of Advanced Science and Technology, 51, 2013.
- Farzin Piltan, M.H. Yarmahmoudi, M. Mirzaei, S. Emamzadeh, Z. Hivand, “Design Novel Fuzzy Robust Feedback Linearization Control with Application to Robot Manipulator”, International Journal of Intelligent Systems and Applications, 5(5), 2013.
- Sh. Tayebi Haghighi, S. Soltani, Farzin Piltan, M. kamgari, S. Zare, “Evaluation Performance of IC Engine: Linear Tunable Gain Computed Torque Controller Vs. Sliding Mode Controller”, International Journal of Intelligent Systems and Applications, 5(6), 2013.
- Farzin Piltan, A. R. Salehi & Nasri B Sulaiman,“Design Artificial Robust Control of Second Order System Based on Adaptive Fuzzy Gain Scheduling”, World Applied Science Journal (WASJ), 13 (5): 1085-1092, 2011.
- Farzin Piltan, N. Sulaiman, Atefeh Gavahian, Samira Soltani & Samaneh Roosta, “Design Mathematical Tunable Gain PID-Like Sliding Mode Fuzzy Controller with Minimum Rule Base”, International Journal of Robotic and Automation, 2 (3): 146-156, 2011.
- Farzin Piltan , N. Sulaiman, Zahra Tajpaykar, Payman Ferdosali & Mehdi Rashidi, “Design Artificial Nonlinear Robust Controller Based on CTLC and FSMC with Tunable Gain”, International Journal of Robotic and Automation, 2 (3): 205-220, 2011.
- Farzin Piltan, Mohammad Mansoorzadeh, Saeed Zare, Fatemeh Shahriarzadeh, Mehdi Akbari, “Artificial tune of fuel ratio: Design a novel siso fuzzy backstepping adaptive variable structure control”, International Journal of Electrical and Computer Engineering (IJECE), 3 (2): 183-204, 2013.
- Farzin Piltan, M. Bazregar, M. Kamgari, M. Akbari, M. Piran, “Adjust the fuel ratio by high impact chattering free sliding methodology with application to automotive engine”, International Journal of Hybrid Information Technology (IJHIT), 6 (1): 13-24, 2013.
- Shahnaz Tayebi Haghighi, S. Soltani, Farzin Piltan, M. Kamgari, S. Zare, “Evaluation Performance of IC Engine: linear tunable gain computed torque controller Vs. Sliding mode controller”, I. J. Intelligent system and application, 6 (6): 78-88, 2013.
- Farzin Piltan, N. Sulaiman, Payman Ferdosali & Iraj Assadi Talooki, “Design Model Free Fuzzy Sliding Mode Control: Applied to Internal Combustion Engine”, International Journal of Engineering, 5 (4):302-312, 2011.
- Farzin Piltan, N. Sulaiman, A. Jalali & F. Danesh Narouei, “Design of Model Free Adaptive Fuzzy Computed Torque Controller: Applied to Nonlinear Second Order System”, International Journal of Robotics and Automation, 2 (4):245-257, 2011
- A. Jalali, Farzin Piltan, M. Keshtgar, M. Jalali, “Colonial Competitive Optimization Sliding Mode Controller with Application to Robot Manipulator”, International Journal of Intelligent Systems and Applications, 5(7), 2013.
- Farzin Piltan, Amin Jalali, N. Sulaiman, Atefeh Gavahian & Sobhan Siamak, “Novel Artificial Control of Nonlinear Uncertain System: Design a Novel Modified PSO SISO Lyapunov Based Fuzzy Sliding Mode Algorithm”, International Journal of Robotics and Automation, 2 (5): 298-316, 2011.
- Farzin Piltan, N. Sulaiman, Iraj Asadi Talooki & Payman Ferdosali, “Control of IC Engine: Design a Novel MIMO Fuzzy Backstepping Adaptive Based Fuzzy Estimator Variable Structure Control”, International Journal of Robotics and Automation, 2 (5):360-380, 2011.
- Farzin Piltan, N. Sulaiman, S.Soltani, M. H. Marhaban & R. Ramli, “An Adaptive Sliding Surface Slope Adjustment in PD Sliding Mode Fuzzy Control For Robot Manipulator”, International Journal of Control and Automation, 4 (3): 65-76, 2011.
- Farzin Piltan, N. Sulaiman, Mehdi Rashidi, Zahra Tajpaikar & Payman Ferdosali, “Design and Implementation of Sliding Mode Algorithm: Applied to Robot Manipulator-A Review”, International Journal of Robotics and Automation, 2 (5):265-282, 2011.
- Farzin Piltan, N. Sulaiman , Arash Zargari, Mohammad Keshavarz & Ali Badri, “Design PID-Like Fuzzy Controller with Minimum Rule Base and Mathematical Proposed On-line Tunable Gain: Applied to Robot Manipulator”, International Journal of Artificial Intelligence and Expert System, 2 (4):184-195, 2011.
- Farzin Piltan, SH. Tayebi HAGHIGHI, N. Sulaiman, Iman Nazari & Sobhan Siamak, “Artificial Control of PUMA Robot Manipulator: A-Review of Fuzzy Inference Engine and Application to Classical Controller”, International Journal of Robotics and Automation, 2 (5):401-425, 2011.
- A. Salehi, Farzin Piltan, M. Mousavi, A. Khajeh, M. R. Rashidian, “Intelligent Robust Feed-forward Fuzzy Feedback Linearization Estimation of PID Control with Application to Continuum Robot”, International Journal of Information Engineering and Electronic Business, 5(1), 2013.
- Farzin Piltan, N. Sulaiman & I.AsadiTalooki, “Evolutionary Design on-line Sliding Fuzzy Gain Scheduling Sliding Mode Algorithm: Applied to Internal Combustion Engine”, International Journal of Engineering Science and Technology, 3 (10):7301-7308, 2011.
- Farzin Piltan, Nasri B Sulaiman, Iraj Asadi Talooki & Payman Ferdosali, ”Designing On-Line Tunable Gain Fuzzy Sliding Mode Controller Using Sliding Mode Fuzzy Algorithm: Applied to Internal Combustion Engine” World Applied Science Journal (WASJ), 15 (3): 422-428, 2011.
- Farzin Piltan, M.J. Rafaati, F. Khazaeni, A. Hosainpour, S. Soltani, “A Design High Impact Lyapunov Fuzzy PD-Plus-Gravity Controller with Application to Rigid Manipulator”, International Journal of Information Engineering and Electronic Business, 5(1), 2013.
- A. Jalali, Farzin Piltan, A. Gavahian, M. Jalali, M. Adibi, “Model-Free Adaptive Fuzzy Sliding Mode Controller Optimized by Particle Swarm for Robot manipulator”, International Journal of Information Engineering and Electronic Business, 5(1), 2013.
- Farzin Piltan, N. Sulaiman, Payman Ferdosali, Mehdi Rashidi & Zahra Tajpeikar, “Adaptive MIMO Fuzzy Compensate Fuzzy Sliding Mode Algorithm: Applied to Second Order Nonlinear System”, International Journal of Engineering, 5 (5): 380-398, 2011.
- Farzin Piltan, N. Sulaiman, Hajar Nasiri, Sadeq Allahdadi & Mohammad A. Bairami, “Novel Robot Manipulator Adaptive Artificial Control: Design a Novel SISO Adaptive Fuzzy Sliding Algorithm Inverse Dynamic Like Method”, International Journal of Engineering, 5 (5): 399-418, 2011.
- Farzin Piltan, N. Sulaiman, Sadeq Allahdadi, Mohammadali Dialame & Abbas Zare, “Position Control of Robot Manipulator: Design a Novel SISO Adaptive Sliding Mode Fuzzy PD Fuzzy Sliding Mode Control”, International Journal of Artificial Intelligence and Expert System, 2 (5):208-228, 2011.
- M. M. Ebrahimit Farzin Piltan, M. Bazregar and A.R. Nabaee “Intelligent Robust Fuzzy-Parallel Optimization Control of a Continuum Robot Manipulator”, International Journal of Control and Automation, 6(3), 2013.
- Farzin Piltan, M.A. Bairami, F. Aghayari, M.R. Rashidian, “Stable Fuzzy PD Control with Parallel Sliding Mode Compensation with Application to Rigid Manipulator”, International Journal of Information Technology and Computer Science, 5(7), 2013.
- Farzin Piltan, N. Sulaiman, Samaneh Roosta, Atefeh Gavahian & Samira Soltani, “Evolutionary Design of Backstepping Artificial Sliding Mode Based Position Algorithm: Applied to Robot Manipulator”, International Journal of Engineering, 5 (5):419-434, 2011.
- Farzin Piltan, N. Sulaiman, Amin Jalali, Sobhan Siamak & Iman Nazari, “Control of Robot Manipulator: Design a Novel Tuning MIMO Fuzzy Backstepping Adaptive Based Fuzzy Estimator Variable Structure Control”, International Journal of Control and Automation, 4 (4):91-110, 2011.
- Farzin Piltan, N. Sulaiman, Atefeh Gavahian, Samaneh Roosta & Samira Soltani, “On line Tuning Premise and Consequence FIS: Design Fuzzy Adaptive Fuzzy Sliding Mode Controller Based on Lyaponuv Theory”, International Journal of Robotics and Automation, 2 (5):381-400, 2011.
- Farzin Piltan, N. Sulaiman, Samira Soltani, Samaneh Roosta & Atefeh Gavahian, “Artificial Chattering Free on-line Fuzzy Sliding Mode Algorithm for Uncertain System: Applied in Robot Manipulator”, International Journal of Engineering, 5 (5):360-379, 2011.
- Farzin Piltan, F. ShahryarZadeh, M. Mansoorzadeh, M. kamgari, S. Zare, “Robust Fuzzy PD Method with Parallel Computed Fuel Ratio Estimation Applied to Automotive Engine “International Journal of Intelligent Systems and Applications, 5(8), 2013.
- Farzin Piltan, Sadeq Allahdadi, Mohammad A.Bairami & Hajar Nasiri, “Design Auto Adjust Sliding Surface Slope: Applied to Robot Manipulator”, International Journal of Robotics and Automation, 3 (1):27-44, 2011.
- Farzin Piltan, Mohammadali Dialame, Abbas Zare & Ali Badri, “Design Novel Lookup Table Changed Auto Tuning FSMC:Applied to Robot Manipulator”, International Journal of Engineering, 6 (1):25-41, 2012.
- Farzin Piltan, M. Keshavarz, A. Badri & A. Zargari, “Design Novel Nonlinear Controller Applied to RobotManipulator: Design New Feedback Linearization Fuzzy Controller with Minimum Rule Base Tuning Method”, International Journal of Robotics and Automation, 3 (1):1-12, 2012.
- Farzin Piltan, Mohammad A.Bairami, Farid Aghayari & Sadeq Allahdadi, “Design Adaptive Artificial Inverse Dynamic Controller: Design Sliding Mode Fuzzy Adaptive New Inverse Dynamic Fuzzy Controller”, International Journal of Robotics and Automation, (1):13-26, 2012.
- Farzin Piltan, Sadeq Allahdadi, Mohammad A.Bairami & Hajar Nasiri, “Design Auto Adjust Sliding Surface Slope: Applied to Robot Manipulator”, International Journal of Robotics and Automation, 3 (1):27-44, 2012.
- Farzin Piltan, F. Aghayari, M. Rashidian & M. Shamsodini, “A New Estimate Sliding Mode Fuzzy Controller for RoboticManipulator”, International Journal of Robotics and Automation, 3 (1):45-60, 2012
- Farzin Piltan, Iman Nazari, Sobhan Siamak, Payman Ferdosali, “Methodology of FPGA-Based Mathematical error-Based Tuning Sliding Mode Controller”, International Journal of Control and Automation, 5(1), 89-118, 2012.
- Farzin Piltan, Bamdad Boroomand, Arman Jahed & Hossein Rezaie, “Methodology of Mathematical Error-Based Tuning Sliding Mode Controller”, International Journal of Engineering, 6 (2):96-117, 2012.
- Farzin Piltan, S. Emamzadeh, Z. Hivand, F. Shahriyari & Mina Mirazaei. ” PUMA-560 Robot Manipulator Position Sliding Mode Control Methods Using MATLAB/SIMULINK and Their Integration into Graduate/Undergraduate Nonlinear Control, Robotics and MATLAB Courses”, International Journal of Robotics and Automation, 3(3):106-150, 2012.
- Farzin Piltan, A. Hosainpour, E. Mazlomian, M.Shamsodini, M.H Yarmahmoudi. ”Online Tuning Chattering Free Sliding Mode Fuzzy Control Design: Lyapunov Approach”, International Journal of Robotics and Automation, 3(3):77-105, 2012.
- Farzin Piltan, R. Bayat, F. Aghayari, B. Boroomand. “Design Error-Based Linear Model-Free Evaluation Performance Computed Torque Controller”, International Journal of Robotics and Automation, 3(3):151-166, 2012.
- Farzin Piltan, J. Meigolinedjad, S. Mehrara, S. Rahmdel. ”Evaluation Performance of 2nd Order Nonlinear System: Baseline Control Tunable Gain Sliding Mode Methodology”, International Journal of Robotics and Automation, 3(3): 192-211, 2012.
- Farzin Piltan, Mina Mirzaei, Forouzan Shahriari, Iman Nazari, Sara Emamzadeh, “Design Baseline Computed Torque Controller”, International Journal of Engineering, 6(3): 129-141, 2012.
- Farzin Piltan, Sajad Rahmdel, Saleh Mehrara, Reza Bayat , “Sliding Mode Methodology Vs. Computed Torque Methodology Using MATLAB/SIMULINK and Their Integration into Graduate Nonlinear Control Courses” , International Journal of Engineering, 6(3): 142-177, 2012.
- Farzin Piltan , M.H. Yarmahmoudi, M. Shamsodini, E.Mazlomian, A.Hosainpour. ”PUMA-560 Robot Manipulator Position Computed Torque Control Methods Using MATLAB/SIMULINK and Their Integration into Graduate Nonlinear Control and MATLAB Courses”, International Journal of Robotics and Automation, 3(3): 167-191, 2012.
- Farzin Piltan, Hossein Rezaie, Bamdad Boroomand, Arman Jahed. “Design Robust Backstepping on-line Tuning Feedback Linearization Control Applied to IC Engine”, International Journal of Advance Science and Technology, 11:40-22, 2012.
- Farzin Piltan, S. Siamak, M.A. Bairami and I. Nazari. ” Gradient Descent Optimal Chattering Free Sliding Mode Fuzzy Control Design: Lyapunov Approach”, International Journal of Advanced Science and Technology, 43: 73-90, 2012.
- Farzin Piltan, M.R. Rashidian, M. Shamsodini and S. Allahdadi. ” Effect of Rule Base on the Fuzzy-Based Tuning Fuzzy Sliding Mode Controller: Applied to 2nd Order Nonlinear System”, International Journal of Advanced Science and Technology, 46:39-70, 2012.
- Farzin Piltan, A. Jahed, H. Rezaie and B. Boroomand. ” Methodology of Robust Linear On-line High Speed Tuning for Stable Sliding Mode Controller: Applied to Nonlinear System”, International Journal of Control and Automation, 5(3): 217-236, 2012.
- Farzin Piltan, R. Bayat, S. Mehara and J. Meigolinedjad. ”GDO Artificial Intelligence-Based Switching PID Baseline Feedback Linearization Method: Controlled PUMA Workspace”, International Journal of Information Engineering and Electronic Business, 5: 17-26, 2012.
- Farzin Piltan, B. Boroomand, A. Jahed and H. Rezaie. ”Performance-Based Adaptive Gradient Descent Optimal Coefficient Fuzzy Sliding Mode Methodology”, International Journal of Intelligent Systems and Applications, 11: 40-52 2012.
- Farzin Piltan, S. Mehrara, R. Bayat and S. Rahmdel. ” Design New Control Methodology of Industrial Robot Manipulator: Sliding Mode Baseline Methodology”, International Journal of Hybrid Information Technology, 5(4):41-54, 2012.
- AH Aryanfar, MR Khammar, Farzin Piltan, “Design a robust self-tuning fuzzy sliding mode control for second order systems”, International Journal of Engineering Science REsearch, 3(4): 711-717, 2012.
- Farzin Piltan, Shahnaz Tayebi Haghighi, “Design Gradient Descent Optimal Sliding Mode Control of Continuum Robots”, International Journal of Robotics and Automation, 1(4): 175-189, 2012.
- Farzin Piltan, A. Nabaee, M.M. Ebrahimi, M. Bazregar, “Design Robust Fuzzy Sliding Mode Control Technique for Robot Manipulator Systems with Modeling Uncertainties”, International Journal of Information Technology and Computer Science, 5(8), 2013.
- Farzin Piltan, M. Akbari, M. Piran , M. Bazregar. ”Design Model Free Switching Gain Scheduling Baseline Controller with Application to Automotive Engine”, International Journal of Information Technology and Computer Science, 01:65-73, 2013.
- Farzin Piltan, M. Piran , M. Bazregar, M. Akbari, “Design High Impact Fuzzy Baseline Variable Structure Methodology to Artificial Adjust Fuel Ratio”, International Journal of Intelligent Systems and Applications, 02: 59-70, 2013.
- Farzin Piltan, M. Mansoorzadeh, M. Akbari, S. Zare, F. ShahryarZadeh “Management of Environmental Pollution by Intelligent Control of Fuel in an Internal Combustion Engine“ Global Journal of Biodiversity Science And Management, 3(1), 2013.


