Designing a Universal Data-Oriented Random Number Generator

Published Online February 2013 in MECS

Random numbers are useful for a variety of purposes such as generating data encryption keys, simulation and modeling uncertain phenomena and for selecting samples from lager data set. Random numbers are modeled by using mathematical function, probability density function or probability mass function. For example the chi-square distribution with degrees of freedom is the distribution of a sum of the squares of independent standard random variables. It is one of the most widely used probability distributions in inferential statistics, e.g. in hypothesis testing, or in construction of confidence intervals.

So far, due to lack of storage memory and it's lowspeed , the problems were solved with much less data lying complex algorithms. nowadays, growing memory technology causes to computing system to manage large amount of data very fast and easily. Data-oriented theory presents methods in which any concept can be modeled in terms of data structures. Thus in modern computing systems Concepts that are modeled with data-oriented theory can be recognized and processed more quickly. In theses models the questions can be answered by data processing or by fewer amounts of mathematical operations. The methods to answer the questions by using large amount of data, are called data–oriented methods [1].

This paper introduced a Universal Random Number Generator, URNG, with uniform, normal, exponential and chi-square distributions based on Data-Oriented theory. This model is compatible with modern computer's structure and it is able to generate random numbers with any distribution and utilize computers in statistical inference and probability with higher speed and productivity. The rest of this paper is organized as follow:

The related work of Data-Oriented modeling and basic definitions to outline URNG, presented in section two. The URNG is designed in section three, section four provides concluding remarks and future works.

• II.    BASIC CONCEPT

The basic structure of data-oriented modeling has been presented to handle structures like Probability Digraph, probability language, complete tree walk and n-complete tree walks [2]. In other words, requirement tools, definition and important mathematical theorems for these models have been presented in [3]. Recently some methods have been presented to model and generate numbers with a given distribution based on data-oriented approach. For example data–oriented models of uniform [4], normal [5], exponential [6] and chi Square random variables [1] have been presented. Each of these models generates random numbers with any given distribution separately, but URNG is suggested, This URNG have been able to generate random numbers with uniform, normal, exponential, and chi-square distributions.

Probability digraph, digital prodigraph, value of walk1, value of leaf2, have been defined in [1]. In this paper we use them and some other definitions are provided as follows:

Definition:

The probability density function of the continuous uniform distribution is defined by equation 1 [4]:

f ( X )={      , a                       (1)

Otherwis0e .

The graph of the uniform distribution for a =2 and b=7 is shown in Fig. 1.

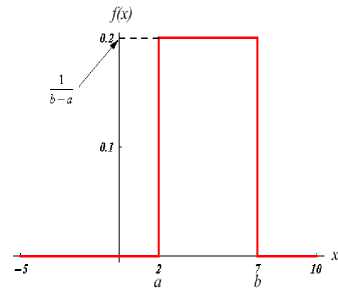
Fig. 1:The graph of the P.D.F. of uniform distribution [11].

Definition:

Let x be of a normal random variable with a mean of µ and variance δ2 , Then the probability density function is reached through equation 2 [5]:

ф(z)=n(X,p,a)= = e 2Z

The normal distribution is probably the most frequently used distribution. The graph of normal distribution is shown in Fig. 2.

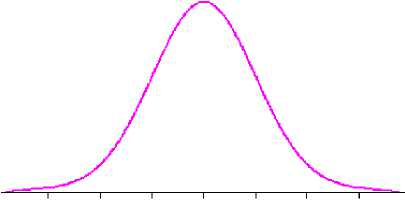
• -3-2-10 1 23c.

Fig. 2: The graph of the P.D.F. of normal distribution [11].

Definition:

In the probability theory and statistics, the exponential distribution is a class of continuous Probability distribution that describe the time between events in a Poisson process. In the formal notation, let x denote the waiting time until the first change occurs when observing a Poisson process, then it has an exponential distribution and its probability density function is defined by equation 3 [6]:

f ( x )=Ле"^Яж    ,0≤ x <∞                (3)

Where X is the parameter of the distribution, called the rate parameter, In this paper we take X =5.

The graph of exponential distribution is shown in Fig.

• 3 [6].

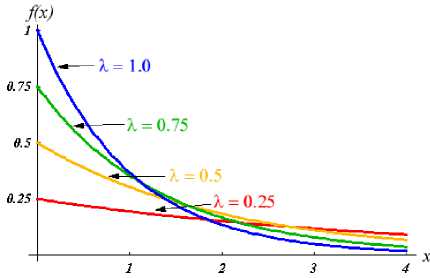
Fig. 3: The graph of the p.d.f. of exponential distribution [6].

Let xi, I=1,2,….,k be a independent and identically distributed Gaussian random variables with mean µ=0 and variance δ2 . A random variable z given by equation 4 is chi-square random variable with a k degree of freedom. it is an important continuous random variable [1].

Z =∑ Ll^i                                (4)

In probability theory and statistics, the chi-square distribution (or x2 distribution) with a k degree of freedom is the distribution of a sum of the squares of k independent random variables. It is one of the most widely used probability distributions in inferential statistics, e.g. in hypothesis testing, or in construction of confidence intervals. The chi-square distribution is a special gamma distribution [1].

Definition:

Let z be a chi-square random variable with a k degrees of freedom, then the probability density function3 is defined by equation 5 [1]:

• ₁       к-2 к

f ( Z , к )=—---- x i e 2, z ≥0.                 (5)

×Г( )

Where Г( ) denotes the gamma function. The gamma function is defined by equation 6:

Г( p )=∫” t^{p г}е ^cdt , p ≥0.                    (6)

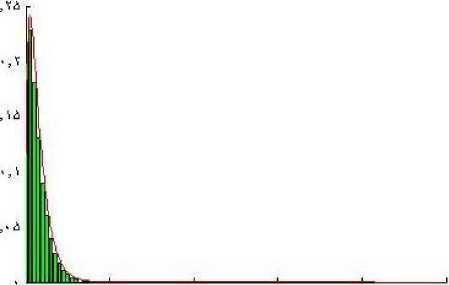
As the number of freedom is increased, the X2 distribution become more symmetrical and when the degrees of freedom become infinitely large, chi-square approaches normality [1]. The graph of chi-square distribution is shown in Fig. 4.

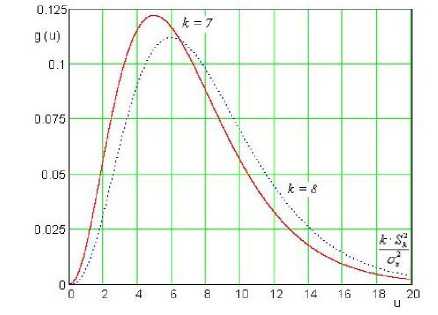
Fig. 4: The graph of the P.D.F. of normal distribution [7].

In this paper we assume k=3 and take the random variable z with 3 degrees of freedom. Then p.d.f. of z is equal to equation 7 [7]:

f (z) =

1 1

^zz e 2

V2F z > 0

Definition:

T is probability complete tree, if and only if the sum of the all adjacent weights of a vertex is either 1 or 0. Trees shown by Fig.1 and Fig.2 are probability complete trees. Note that the vertices have the total adjacency to edge weight of 0 are tree leaves [1].

Definition:

T is an n-complete probability tree if and only if:

• 1.    It is a probability complete tree.

• 2.    Each of vertices that have total adjacency to edge weight of 0 must be in depth n of the tree root.

All leaves must be in depth n, which is the depth of tree. Fig.1 shows a 2-complete probability tree, but the tree represented in Fig. 2 does not since it fails to satisfy the second part of this definition [1].

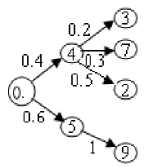
Fig. 5: A digital 2-complete probability tree

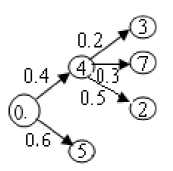
Fig. 6: A digital probabilistically complete tree

Definition:

Let t be a digital n-complete probability tree, and a n be along with its leaf vertex on it. As shown in equation 8:

Vol an =y=0 . a 1 a 2 …a n                                    (8)

Then P y is the probability of vol an , if and only if have equation 9:

P y =P O.a1 *P a1a2 *…*P an-1an =P O.a1 Π i=2 P aiai+1                  (9)

Data-oriented model of random variable z is presented by calculating the probability of digits by AF [11] and then these probabilities are used in probability complete tree as weights. AF is a fact that gives the probability of a random variable's digits by using its density function. In other words Ahmad fact describes the digits of a random variable are randomly distributed and specifies the probability of the kth digit is given of a determined random variable. Suppose that the random variable z has probability density function f(z). p_zi denotes the probability of the first digit of z to be i where i=0,1,2,3,^,9 in decimal base. p_zr is calculated by using AF as realation 10:

p_z i = p( i <  z <  i + 1) = J.ⁱ⁺¹/(z)dz             (10)

As we know, this relation gives the probability that the value of random variable z is in [i, i+1]. Considering AF, this is the probability that the first digit of z is equal i. For example p _z2 shows the probability that first digit of z equal, 2. This notation is used to making digital 1-probability complete tree. By calculating second digit's probability, digital 2-probability complete tree can be made. For this purpose p ij is used. p ij shows the

Z2                Z2

probability that the second digit of z equals j if the first digit has occurred i. p ij is computed from equation 11:

Z2

p_z ч = p( --j < z < i.j + 1) = ^^ ⁺¹/(z)dz       (11)

For example pz 34 is a probability that the z is in [3.4 , 3.5] and considering AF, this is the probability that the second digit of z to be 4 if the first has been equaled to 3. For calculating kth digit probability p ij „m, is used so zk probability of first, second,…, k-1th digits should be given.

Data-oriented theory is used to generate random numbers, In order to generate random number, some array, like digits bank is considered. In order to [1] for generate random number with two digits based on data- oriented theory, P i, Р ij are calculated for i,j=0 to 9 that results for pzi are shown in table 1. Here 11 digits banks are considered and form the value's obtained for Pzi , the first two or three digits after decimal point are selected as the numbers of the iteration number for i are inserted in digits bank. For example if PZ1 = 0.228 , so number 22 is selected which is considered the number of times that 1 is repeated and inserted in digits bank1. Table 2 shows the number of times a number appears in digit bank. Similarly, three digits after decimal point of p ij are selected and inserted in digits bank2…11. After Z2

recording these numbers in the digits banks, and randomly shuffling (or exchange or rotate) the content of them, one number is selected randomly from digits bank1, then depending on the selected numbers, one of the other ten digits banks is selected and froms this newly selected digits bank one element is chosen randomly too. In this method each digits bank has about 1000 elements with 4 bits for each of them that are 11000 elements and 5.5kb memory using in total. The architecture of this case is shown in Fig.8.

Table 1. Probability of fitrst digit

I	0	1	2	3	4	5	6	7	8	9
	0.186	0.228	0.163	0.127	0.091	0.055	0.038	0.027	0.016	0.0103

Table 2. Number of digits in digits bank1

Shuff,Ex..R.

R.N

Out

__t____

*.E Digits bank2

R.N—>E Digits bankl

>E Digits banks —►

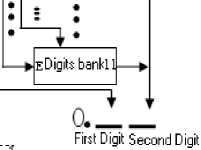
Shff: Shuffle Ek_: Exchange Fl.: Rotate R.N: Random number E: Enable

Fig. 7: Architecture of random number generator.

• III.    UNIVERSAL RANDOM NUMBER GENERATOR

Simulation result shows the random number generator with two digits has more precision, but needs more memory space [1] and each of these models generates random numbers with any given distributions separately, but we suggest universal random numbers generator with less memory space. In this section U.R.N.G is designed as follow:

From the values obtained for p ij as shown in table3,

Z2

the first three digits after decimal point are selected as the numbers of the iteration number for ij in numbers bank. In this paper instate of 11 digits banks, one number bank for each distribution is considered and by calculating p ij for all i,j, distributions and inserting

Z2 "

selection results in number banks, UDRNG can start, At first the type of distribution input by device and depending on the input distribution, one of the four numbers bank is selected, and by generating 2-bits digit randomly, content of selected numbers bank is shuffled or exchanged or rotated. Then from selected number bank, one element is chosen randomly.

Simulation results are shown in Fig.9 (a-d). With this method we can achieve a universal and cumulative random numbers.

The hardware structure of URNG is shown in Fig10, to implementation URNG in hardware structure we consider special memory or cache instate of numbers banks, decoder to select region of each distribution, 2-bit counter to select operation based on table3 for mix the content of cache.

Table 1: Number of digits in digits bank

Dist. P\I 0 1 2 3 4 5 6 7 8 9 Uniform Pn‘ P UO Pu? Pu2 Pu3 Pu4 Pu5 Pu6 Pu7 Pu8 ^uX Normal PN‘ P N? Pn? Pn? PnI Pn^ Pn? PN? PN? PN? Pn? Exponential PEi Pe? PE? PE? PE? PE? PE? Pe? PE? Pe? PE? Chi-square Pci Pc? pc; Pc? Pc? Pc? pc? Pc? Pc? Pc? Pc? у t/" U.R.N Generated With Architecture '

*,л

*,t

*,f

*,Y

-Г*»       *       X**      f* *      ?** Ам Ь**

Random number v .'' "

Fig.8.(a) UDRNG for normal distribution

KSQ.R.N Generated with Architecture '

й           f.          ?.           л< I

Random number >...'"

Fig.11.(d) UDRNG for exponential distribution

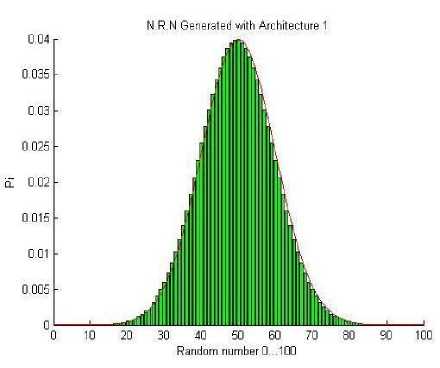
Fig.9.(b) UDRNG for uniform distribution

Cache Memory

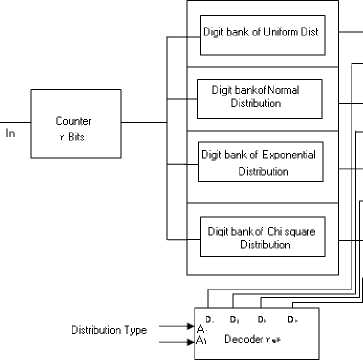
Fig.12: Hardware of universal random number generator

X

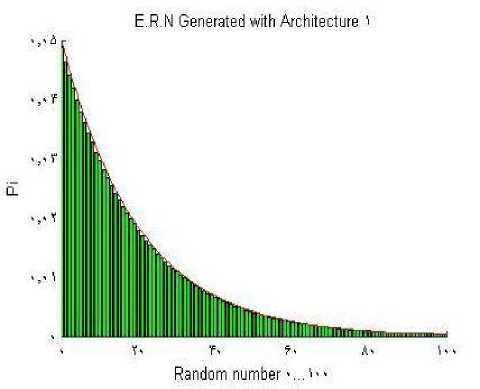
Fig.10.(c) UDRNG for chi-square distribution

Table 4: Instruction set

operation	Op-code
Shuffle	00
Rotate to right	01
Exchange	10
Rotate to left	11

Now table 3 has some parameters in 2000 uniform numbers generated and 1000 numbers generated. Simulation is performed by MATLAB software and some parameter are shown in table3 that mean of square error (MSE) for uniform is achieved from 11 and for other distributions achieved from12.

MSE _{=  ∑} t=o ( т-ft -∫ z ^{(  )} fs ⁽ S ⁾ ds )            (12)

MSE _{=   ∑} So ( rfi -∫⁽t₊l ⁾ fs ⁽ S ⁾ ds )              (13)

where rf i is the relative frequency of generated numbers in the interval [0.i,0.(i+1)] and

Table 5: Parameters table

Distribution	MSE	Memory cells used
Uniform	5.2e-5	1000*10bit=1.25kb
Normal	0.0253	1000*10bit=1.25kb
Exponential	0.0215	1000*10bit=1.25kb
Chi square	0.1219	1000*10bit=1.25kb

Rasoul farjaminezad is a Science Research in Computer Engineering at the Department of Computer Islamic Azad University-Tabriz Branch

• IV.    CONCLUSION AND FURTHER WORKS

In this paper we presented a universal random number generator based on data-oriented to generate random number with uniform, normal, exponential and chisquare distributions. We believe that still we can decrease memory consumption by new techniques.