Детализированная модель динамики структурированной популяции

В агропромышленном секторе экономики одной из важных задач является планирование оборота стада сельскохозяйственных животных [10], [11]. Оборотом стада называется происходящая во времени совокупность процессов, включающая переход животных из одной стадии (категории) в другую, удаление животных разных стадий из стада и появление потомства.

В качестве основы для построения модели стада может быть использовано понятие структурированной популяции. В математической биологии под этим понимают множество проживающих в одной локации организмов одного вида, дискретно разбитых на некоторые классы по какому-либо признаку. Группы могут определяться полом, начальным и конечным возрастом и другими существенными для целей моделирования признаками. Поэтому в описании структурированных популяций используют понятие последовательных стадий жизни организма.

Состояние популяции, разделенной на некоторое число стадий, рассматривается в равноотстоящие дискретные моменты времени и описы-ваетсявектором-столбцом X ( t ) = ( x t _д, x_t 2 ₂ ,..., x_t n ) ^T , где x t i - численность организмов, отнесенньтх к стадии i , n - количество стадий. Динамика популяции задается соотношением

X(t +1) = L • X ( t ), t = 0, 1, .„, (1) определяющим состояние популяции в момент t + 1 по состоянию в момент t посредством матрицы L t , которую называют проекционной. В общем случае элементы проекционной матрицы могут зависеть от времени.

РАЗВИТИЕ МОДЕЛЕЙ СТРУКТУРИРОВАННЫХ ПОПУЛЯЦИЙ

Простейшим вариантом модели (1) является модель Лесли [8], в которой стадиями являются © Пойколайнен В. В., Сиговцев Г. С., 2011

возрастные группы, а проекционная матрица имеет вид:

b l ^Ь 2     ... b n - 1 b n

	S 1     0    ...     0     0
L =	0 s 2 ...    0     0	,                   (2)

0    0    ...    S n - 1     0

0 < b i - коэффициент рождаемости для стадии i , 0 <  s i <  1 — коэффициент дожития (перехода из стадии i в стадию i + 1).

Если для квадратной матрицы A порядка n и ориентированного графа G с n вершинами, пронумерованными числами от 1 до n , существует взаимно однозначное соответствие между ненулевыми элементами a . и дугами ( i , j ), то такой граф называется ассоци^, ированным с матрицей и обозначается G(A). Граф, ассоциированный с проекционной матрицей структурированной популяции, называют графом жизненного цикла (ГЖЦ) организмов данной популяции.

Для модели Лесли ГЖЦ изображен на рис. 1.

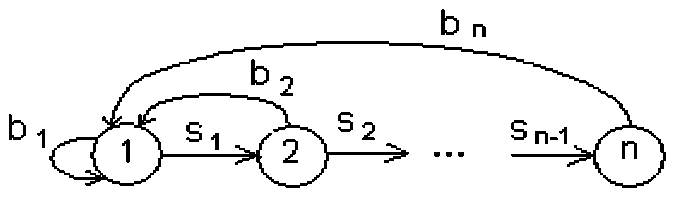
Рис. 1. ГЖЦ модели Лесли

В модели Лесли на каждом шаге происходит полное обновление состава каждой возрастной группы, что является достаточно жестким ограничением для практического использования этой модели. Более общей является модель Лефковича [8], в которой часть особей каждой стадии остается в той же стадии при переходе к следующему моменту времени. Проекционная матрица модели Лефковича имеет вид:

	" b 1 + r	b 2     .	••    bn - 1	b n "
	s 1	Г 2      .	..     0	0
L =	0	s 2     .	..     0	0	,                               3
	. 0	0.	..     sn - 1	r n _

где г. - коэффициент задержки, 0 <  s + r < 1.

ГЖЦ для модели Лефковича изображен на рис. 2.

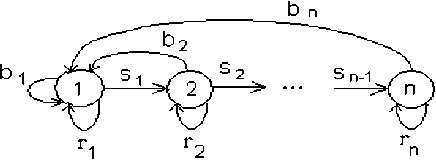
Рис. 2. ГЖЦ модели Лефковича

ГЖЦ на рис. 1 и 2 показаны для случая, когда все параметры проекционных матриц b i , r > 0. Если какой-то из этих параметров равен нулю, то соответствующая дуга ГЖЦ отсутствует.

С математической точки зрения модели Лесли и Лефковича достаточно хорошо изучены [6], [8]. Основные их свойства связаны с теоремой Перрона - Фробениуса для матриц с неотрицательными элементами [2; 130]. В соответствии с этой теоремой спектральный радиус неотрицательной неразложимой матрицы равен максимальному положительному собственному числу. Это число имеет кратность 1, ему соответствует положительный собственный вектор, и оно возрастает при увеличении любого элемента матрицы.

Неразложимость матрицы эквивалентна тому, что ассоциированный с ней орграф сильно связен (для любой пары вершин существует ориентированный путь из одной вершины в другую). В частности, проекционные матрицы моделей Лесли и Лефковича неразложимы, если b n > 0 (последняя стадия популяции является репродуктивной).

Таким образом, спектральный радиус проекционной матрицы р ( L ) = X _max - положительное собственное число матрицы L кратности 1.

Асимптотика вектора X(t), определяемого соотношением (1), при t ^ го зависит от величины спектрального радиуса р ( L ) следующим образом:

Р (L ) >  1 x , , _t ^ « ,

р ( L ) <  1 x. t ^ 0 ,                        ⁽⁴⁾

Р(L) = 1 xi,t ^ x,*, для каждой стадии г = 1, ..., n.

Последний случай означает устойчивость по -пуляции: ее численность в каждой стадии стре- мится к конечному пределу, не зависящему от начальной численности популяции. При этом из уравнений (1) для матрицы L вида (3) следует, что предельные численности стадий в модели Лефковича связаны следующими соотношениями:

x*, + 1 = ₁ si    • x*, , i = 1, ..., n - 1,

^{1 -} r + 1

*

x ₁

1 - b 1 - r

n

• I bx ‘.

= 2

Следствием соотношений (5) является условие:

^b 1 ⁺ r 1 ⁺ I b • q , = i, где q , = П s j^- .      ⁽⁶⁾

I = 2                            /=1 1 ^- rj + 1

Так как вектор предельных численностей X является собственным вектором проекционной матрицы, соответствующим собственному числу X _max = 1, то условие (6) - это условие стабильности популяции. Условие (6) соответствует приведенному в [3] результату об индикаторе потенциального роста популяции в модели Лефковича.

Собственный вектор X при условии, что n

I x *• = 1 , называется относительной стадийной г = 1

структурой популяции [6].

Из соотношений (5) следует, что вектор относительной структуры популяции в модели Лефковича имеет вид:

T n , n ,.-., n

1+ I q , 1+ I q,   1+ I q ,

\       i = 2             i = 2                 i = 2     /

Условие bn > 0 не является принципиальным ограничением для применения описанных выше моделей [8; 58]. Наличие в модели популяции пострепродуктивных стадий не влияет на динамику стадий популяции с номерами от 1 до n (последняя репродуктивная стадия), которая по-прежнему определяется матрицей (3). Численность пострепродуктивных стадий опре- деляется соотношением:

^x„ + . , t + 1 = s n + , - 1 • ^xn + , - 1, t ⁺ r + , • ^xn + i,t , i = 1, -^, m ,           (7)

где m - количество таких стадий.

ГЖЦ модели с пострепродуктивными стадиями показано на рис. 3.

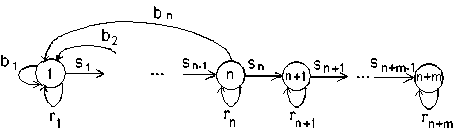
Рис. 3. ГЖЦ модели с пострепродуктивными стадиями

Данный граф не является сильно связным (отсутствуют пути из вершин n + 1, …, n + m в вершины 1, …, n ); соответственно, проекционная матрица L такой модели разложима. Она имеет вид:

L 0

SM

где L – матрица (3), M – m × n – матрица переходов для пострепродуктивных стадий

r n + 1

L =	" b 1 + Г 1 s 21 s 31	b 2 r 2 s 3 2	-   bn - 1 ...      0 ...      0	b 1 n 0 0	(10)
	[ s n 1	s n 2	...    nnn - 1 n	r n .
при условии, что ..., n – 1.		0 <  r j	+ Z s-^ 1 i = j + 1	для всех j = 1,

M =

s n + 1

r n + 2

s , r n + m - 1     n + m

S – m × n –

матрица с единственным ненулевым элементом s_n в правом верхнем углу, связывающим стадии n и n + 1.

Вектор состояния популяции X ( t ) = ( x_{t ,1} , x_{t ,2} , ..., x_{t , n} ) ^T может быть разбит на два вектора X ^I ( t ) = = ( x_{t ,1} , x_{t ,2} , ..., x_{t , n} ) и X ( t ) = ( x_{t , n +1} , x_{t , n +2} , ..., x_{t , n+m} ) . Изменение численности популяции описывает-

ся системой уравнений:

[ X I ( t + 1) = L ■ X I ( t )

.

X " ( t + 1) = 5 ■ X I ( t ) + M ■ X ” ( t )

Асимптотика вектора X ^I ( t ), определяемого соотношением (9), при t → ∞ по-прежнему зависит от величины спектрального радиуса ρ ( L ) так, как это указано в (4).

Характер асимптотики вектора X ^II ( t ) однозначно определяется поведением вектора X ^I ( t ) при t ^ да. Если lim x_ti = x * , i = 1, ..., n, то по ин- ^ro ^,

дукции доказывается, что существуют пределы x_{t,n + i} для i = 1, ..., m при t → ∞.

Из (7) также следует, что если lim x_ti =» , i = 1,

^да ^,

..., n, то lim x_t n ₊ i = да для всех j = 1, ..., m . t ^to ^,

Вектор относительной структуры популяции имеет такой же вид, как и выше (с распространением суммирования по i от 2 до n + m ).

В работах Д. О. Логофета и других [5], [6], [7] рассмотрены некоторые обобщения моделей Лесли и Лефковича, связанные с необходимостью в некоторых случаях классифицировать особей популяции по нескольким признакам. Например, в [14] модель популяции северных оленей учитывает их возраст и статус («сильный», «средний», «слабый»).

Такого типа модель может быть записана в форме матричного уравнения (1), если матрицу двойной структуры популяции (строкам матрицы соответствует возраст, а столбцам – статус особи) представить в виде вектора, образованного конкатенацией строк [5]. Проекционная матрица такой модели, называемая обобщенной матрицей Лефковича или матрицей Логофета [4], в общем случае имеет вид:

Для матрицы (10) также существует выражаемый через элементы матрицы индикатор потенциального роста [6], обобщающий условие существования стабильной популяции (6).

В ряде работ указывается, что матричные модели не всегда удается должным образом применить для решения некоторых практических задач ввиду недостаточно явно представленной динамики популяции [3]. Например, в работах [13], [15] предлагается детализировать матричный подход к расчету динамики структурированной популяции, разложив его на «скрытые» субпроцессы. Из состояния популяции X_t в момент t рассчитывается численность выживших за шаг времени X_S ( t ), затем взросление X_A ( t ) и получение потомства X_B ( t ), таким образом получается численность популяции в момент t + 1: X ( t ) ^ X_s ( t ) ^ X A ( t ) ^ X B ( t ) ^ X ( t + 1) . Такая детализация динамики в некоторой степени упрощает определение модельных параметров.

Дискретные модели широко применяются для описания эксплуатируемых популяций, когда производится регулируемое изъятие некоторой части особей, принадлежащих определенным стадиям, а также для постановки и решения оптимизационных задач [9], [11].

ДЕТАЛИЗИРОВАННАЯ МОДЕЛЬ СТРУКТУРИРОВАННОЙ ПОПУЛЯЦИИ

Популяции типа стада сельскохозяйственных животных относят к эксплуатируемым популяциям, хотя для них характерны не только процессы изъятия части особей, но и добавление извне новых особей, а также другие целенаправленные воздействия управляющего субъекта, влияющие на состав и численность популяции. В этом случае более адекватным будет термин «управляемая популяция».

Использование дискретной модели динамики управляемой популяции для задачи планирования оборота стада сельскохозяйственных животных и рассмотрения на этой основе оптимизационных задач планирования работы агрохо-зяйственного предприятия требует более детального анализа динамики численности. В задачах планирования, как правило, расчеты производятся на определенный временной промежуток, разделяемый на несколько равных периодов длиной T.

Особи стада могут находиться в одной из n стадий, принадлежность к которым определяется возрастом особи т_к , измеряемым в некоторых единицах дискретного модельного времени t = 0, 1 ..., m . Каждой стадии i соответствует свой возрастной промежуток [ т . 1 , т. 2 ]; промежутки разных стадий не пересекаются. Задан предельный возраст T m = m , при достижении которого все особи из популяции изымаются.

Будем считать величину периода T равной некоторому количеству единиц модельного времени. Обозначим через T = т. ₂ - т. 1 продолжительность стадии i . В задачах планирования оборота стада обычно T >  minT. [10], [11], поэтому за один период особь может пройти несколько стадий. Такая же возможность существует и для особи, родившейся в течение этого периода.

Основа детализации модели - в рассмотрении изменений численности различных стадий популяции за единицу модельного времени за счет изменения возраста особей с учетом изъятия части особей и появления особей-потомков.

Пусть заданы функция h ( т, t ) - доля изымаемых в момент времени t особей возраста T в общей численности особей этого возраста, и функция g ( т, t) - коэффициент репродуктивности особей возраста на момент времени t . Если обозначить Y ( t ) = ( y_t 1 , y_{t 2},..., y_tm ) ^T вектор, компонентами которого явлЯют , ся чиСленности особей каждого возраста в момент времени t , то для него будет справедливо соотношение вида (1) Y ( t + 1) = -Л _t • Y ( t ) , где Л _t имеет вид матрицы Лесли:

Л t -

е

e q

в т

0   0   ...   <- 1

вк = g(тк, t), ^к = 1 — h(тк , t), q - номер начального возраста первой репродуктивной популяции.

Для вектора X ( t ) = ( x, ,1 , x_t ,₂ , ..., x, , _n ) ^T численностей стадий популяции соотношение (1) будет иметь место с проекционной матрицей L , имеющей вид матрицы Лефковича

	r t    .	..    b p    .	..     Ь П
	s 1 .	.. 0       .	..     0
L -	0.	г1	..     0
		.. p .

0   0   ...    s n - 1    r

Элементы матрицы L t определяются через элементы матрицы Л _t , p - номер первой репродуктивной популяции. _y

Обозначим через Л - _m ^{t , к} долю особей по-

X у, ,j j=1

пуляции возраста тк во всей численности попу- ляции, fkt =

fkt

X f t

- долю особей популяции воз- j е Ki раста тк, принадлежащего i-й стадии в численности этой стадии популяции (Ki - множество индексов, принадлежащих диапазону возрастов особей стадии i). Тогда для элементов матрицы Lt получаем :

si= <_2■ f_2, bi-Xe,-f,, ri-  Xjf je к.                     je к.\{ i _2}

Структурированная численность популяции через плановый период времени T будет опреде -ляться для возрастной модели соотношением:

Y(T ) -Л^{( T )} ■ Y (0),                  (11)

Л(T) -Л1 ■Л.2 ■...■Лi, где l - количество единиц мо- дельного времени в периоде.

В том частном случае, когда проекционные матрицы детализированной модели не зависят от времени ( Л , -Л ) , имеем л ^{( t )} -Л ¹ и для спектрального радиуса р ( Л ^T ) ) = [ р ( Л )] ¹ . В этом случае каждый из вариантов условий (4) для матриц детализированной и недетализированной моделей выполняется одновременно, и для выяснения устойчивости популяции достаточно проверки условия (6), которое для матрицы Л имеет вид:

m          i - 1

X в . чп ^ -) = ! • i - q         j - 1

При моделировании популяции типа стада крупного рогатого скота более реалистичны нестационарные модели, когда зависимость параметров детализированной возрастной (а следовательно, и стадийной) модели от времени носит сезонно-циклический характер. Но если l кратно длине цикла изменения параметров, то матрица Л ⁽ T ) от времени не зависит. При этом возможно выполнение условия устойчивости популяции р (Л ⁽ T ) ) - 1 в ситуации, когда спектральные радиусы л , в разные моменты модельного времени принимают значения как больше, так и меньше единицы.

Структура проекционной матрицы планового периода T Л ⁽ T ) при T <  q показана на рис. 4.

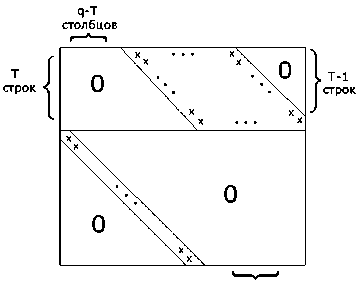
Т-1 столбцов

Рис. 4. Структура матрицы Л ⁽ T )

Элементы, отмеченные значком х, выражаются через значения величин в, о матриц-сомножителей; остальные элементы равны нулю.

Элементы поддиагонали с номером T имеют вид:

j + T - 1

a, j = 1 l " ^{k -} j ^{+ 1} , j = ¹ -’ m ^{- T} , i = ^{T +} j ,         (12)

r = j

а элементы параллелограмма в верхней части

матрицы имеют вид:

a

' i, j

g T ^- i + 1 P t - i+j

' T - i

П<- 1 , к = 1

i - 1

П

к = 1

к - i + T + 1

" к

основана на идее степенного метода нахождения наибольшего по модулю собственного числа матрицы [12].

Если квадратная матрица A порядка n - матрица простой структуры (то есть имеет n линейно независимых собственных векторов) и zk = Ak • z0, к = 1, 2 ..., то для всех значений индекса i = 1,..., n limlz-!!)^ = х, (15) к^” (zk )i

i = 1, ..., T, j = q - T + i,..., m - T + i .        (13)

Если в (13) в одном из произведений верхняя граница индекса равна нулю, то произведение считается равным единице.

Для стадийной модели проекционная матрица планового периода L ^T ) может быть получена путем агрегации элементов матрицы Л ^{T )} , относящихся к одной стадии. Для этого на матрицу Л ^T ) накладывается прямоугольная сетка с ячейками K , i , j = 1,..., n . K принадлежат элементы матрицы Л ^T ) a u v , где u g K i . Ячейке K i ^ соответствует элемент d i j матрицы L ^{( T} ) .

Так как x_T , = Z y_T , _l , из (11) получаем:

l G K i

где X - наибольшее по модулю простое собственное число матрицы A . (15) имеет место для произвольного вектора z ₀ , имеющего ненулевой коэффициент C при соответствующем X собственном векторе x в разложении по базису из собственных векторов. При этом

m

m

/

X T , i = Z | Z a , и У 0, u l = Z Z a , u l У 0,u

l G K i V u = 1

u = 1 V l G K i

n

/

/

= Z Z Z a i,u

j = 1

V u G K j V l G K i

^   ^

^У 0, u

7   7

z_k ^ Х^кСх при k ^ ^ . (16)

В [1; 242] показано, что равенство (15) остается в силе и для матрицы, не обладающей простой структурой, при условии, что X - единственное максимальное по модулю собственное значение единичной кратности. (Матрица, имеющая единственное собственное число с максимальным модулем, называется примитивной.)

Для проекционных матриц рассматриваемых моделей справедлива теорема Перрона -Фробениуса, по которой кратность максимального по модулю собственного числа равна единице. Как показано в [8; 64], матрицы Л t и L_t будут примитивными, если какие-то два соседних элемента их первых строк отличны от нуля. Для матрицы L_t , кроме того, для примитивности достаточно отличия от нуля хотя бы одного элемента r i [2; 132]. Примитивность матриц Л ^{( T} ) и L ^{( T} ) следует из того, что они являются произве-

Соотношение X(T ) = L ^{( T} ) выполняется, если

Г ^

Z ^d-,j x o , j = Z Z ^a >.u y o , u l , где a i,u = Z a iu .

j=1                 j=1 uGK,             )                      l GK, ji

Отсюда получаем: d i ., j =

Za v l,uy o,u uGKj

Z y ou u G K j

Разделив числитель и знаменатель на начальную численность популяции, получаем формулу для вычисления элементов матрицы L^(T ) :

d i, = Z a , u f u .                 (14)

u G K j

В общем случае получение явных выражений для элементов матриц Л(T) и L(T), необходимых для проверки условий типа (6) или вычисления индикатора потенциального роста [6], весьма трудоемко. Эти проверки можно заменить вычислительной процедурой, результаты которой могут быть использованы как «эмпирический» индикатор потенциального роста. Процедура дениями примитивных матриц.

Таким образом, для получаемых с помощью проекционных матриц итерационных последовательностей векторов будут справедливы соот-( Zh+1)-              к ношения (15) и (16). Обозначим------через w^.

( z- ) i               i

В соответствии с (15), если X >  1, то для любой координаты i начиная с некоторой итерации w^k >  1, и наоборот, неравенство w^k >  1 свидетельствует, что X >  1. Аналогично, если начиная с некоторой итерации w^k <  1, то X <  1. При этом из (16) следует, что |( z_k ) i | ^» или |( z_k ) i | ^ 0

соответственно.

Пусть теперь X = 1. В этом случае w^k ^ 1 при к ^ го . Характер стремления w^k к 1 может быть как монотонным, так и немонотонным.

О степени близости отношения w^k к величине X на практике можно судить по совпадению (с некоторой точностью) значений этого отношения для разных значений индекса i [12; 331].

Таким образом, величина отношения w_i^k , полученная после некоторого количества итераций, может играть роль численного индикатора потенциального роста. Необходимое количество итераций определяется в каждом конкретном случае потребностью различить, какой именно из трех возможных вариантов для величины λ (больше, меньше, равно 1) имеет место.

В качестве примера рассмотрим упрощенный вариант детализированной модели, соответствующей модели оборота стада крупного рогатого скота, предложенной А. А. Трофимовым [11].

Исходные данные: предельный возраст особей m = 12, функции h , g зависят только от возраста особей и имеют вид: h ( τ ) = {0,2, 0,05, 0,05, 0,05, 0,03, 0,03, 0,03, 0,03, 0,04, 0,04, 1}, g( τ ) = {0, 0, 0, 0, 0, 0, 0, 0,3, 0,4, 0,6, 0,4, 0,2}. Количество стадий n = 3, возрастные диапазоны стадий: K ₁ = {1, 2, 3}, K ₂ = {4, 5, 6, 7}, K ₃ = {8, 9, 10, 11¹, 12}. Возрастная структура популяции f ( τ ) = {0,15, 0,12, 0,1, 0,08, 0,08, 0,08, 0,06, 0,1, 0,08, 0,05, 0,05, 0,05}, T = 6.

В рассматриваемом примере матрица Лt детализированной модели не зависит от времени, Л(т) = Л6. Вид этих матриц не приводится ввиду их громоздкости. Элементы проекционных матриц стадийной модели вычисляются по форму- лам (11), (14), и эти матрицы имеют вид соответственно:

0,63	0	0,37		0,07	0,86	0,15
0,26	0,78	0	, L т ) =	0,26	0,15	0,69
0	0,19	0,82		0,47	0,64	0

Максимальные по модулю собственные числа: X (Л) = 1,010, X ( Л T ) ) = 1,064, X ( L ) = 1,014, X (Л⁽ T ) ) = 1,097. Применение степенного метода дает следующие результаты: первые три знача- ( z )

щие цифры отношения p+1 i и максимального (zp)i по модулю собственного числа совпадают для Л(T) начиная с пятнадцатой итерации, а для L(T) – начиная со второй. (Начальные вектора z0 имели единичные компоненты.)

Предложенные в данной статье матричные модели структурированных популяций применительно к задаче оборота стада сельскохозяйственных животных позволяют анализировать последствия управляющих воздействий на популяцию. Воздействия в виде изъятия части особей учитываются через изменение функции изъятия h ( τ, t ), а добавление особей в стадо учитывается через изменение функции f ( τ, k ), описывающей возрастную структуру популяции.