Detection of different brain diseases from EEG signals using hidden markov model

Published Online October 2019 in MECS

The applications of Electroencephalography (EEG), as a brain signal, is expanding worldwide, mainly for diagnostic purposes and preventive measures of neurological diseases such as epilepsy, stroke, Parkinson’s diseases and others. The continuous monitoring of EEG signals is necessary to observe the electrical activity of the brain to evaluate drug intoxication, trauma and blood flow during surgical procedures. A key advantage of EEG is that it provides higher temporal resolution than other available brain signals as it responds to the cognitive activities of a subject very rapidly (0.5-130 milliseconds).

Hidden Markov Model (HMM) is a non-linear probabilistic classifier and it provides the probability of a given set of series in time domain. As a non-linear classification technique, it shows higher classification accuracy than those of linear classifiers, for example, linear discriminant analysis (LDA) and support vector machine (SVM). In recent years, HMM has been applied in the various fields of bioinformatics, data mining, pattern recognition, data analysis, wireless networks etc. Some notable works in recent times are protein secondary structure prediction based on a HMM model for data mining [1], offline recognition cursive of Arabic handwritten text without explicit segmentation [2], muscle-computer interface based on HMM state transitions which uses ultrasound sensing [3], action recognition by Gaussian-Mixture HMM (GMM-HMM) model which yields a greater recognition accuracy [4].

HMM has made its mark in different medical, biology and rehabilitation fields; for example, identifying movement states of Parkinsonian patients [5], personal identification system [6], functional brain networks [7], quantification of wheezing for respiratory sound classification [8], single-molecule data analysis in time series which accommodates complications such as drift [9]. Septic shock of critical care patient causes multiple organ failure and eventual death. A HMM model which predicts septic shock for ICU patients [10]. Rehabilitation of a deaf person is done by a DNN-HMM hybrid system for lip-reading and audio visual speech recognition (AVSR) [11], fall detection and real-life home monitoring for senior citizens [12], emotion classification by a combined SVM-HMM classifier to recognize human emotion states based on EEG signals [13]. Already a stacked HMM model has found its applications in robotics for motion intention recognition based on motion trajectories [14].

Other recent and notable studies of HMM include removal of EEG artifact caused by eye blinks [15], seismocardiography learning based on expectationmaximization algorithm and Viterbi algorithm [16], automatic volcano-seismic events detection based on HMM with state and event duration models [17], neural prosthesis to restore efficient communication to people with motor neurological injury [18], obstructive sleep apnea (OSA) detection based on ECG signals [19], 3D catheter tip tracking inside the patient’s 3D vessel tree using 2D X-ray image sequences and a peri-operative 3D rotational angiography (3DRA) [20], palm rehabilitation with supervised learning[21], automatic significant beats extraction in Holter register and feature extraction of ECG signals [22]. Many studies, mostly of functional near-infrared spectroscopy (fNIRS) have successfully demonstrated the use of LDA, SVM and ANN for BCI [23]. Application of machine learning methods has been conducted to combine the EEG-fNIRS signals [24].

We have proposed a methodology in this paper which will classify the EEG signals using HMM technique. The key advantages of HMM are high classification accuracy, provision to add more states etc. as we have found in our research. However, as a brain imaging technique EEG provides lower spatial resolution as compared with fNIRS.

• II.    Methodology

• A.    EEG Signal Acquisition System

Electrodes are likely to be placed on the frontal region for the EEG data acquisition. The positions for electrode placements are Frontal polar 1(Fp1) and Frontal polar 2 (Fp2). For the single channel data acquisition process positive electrode is placed on the Fp2 position, reference electrode is placed on the Fp1 position and negative electrode is placed on A1 (earlobe) position according to international 10-20 electrode system (Fig.1).

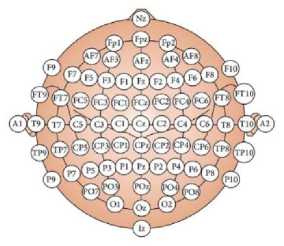
Fig.1. Electrode placement system in 10-20 electrode system

• B.    EEG Signal Conditioning System

Signal conditioning unit has been designed to amplify the EEG signals for further processing (Fig.2). EEG signals picked up using electrodes have a magnitude of around 5-500μV and frequency range of 1-100 Hz, as the most information of EEG signals lie in this range. The integrated single supply instrumentation amplifier is designed based on a typical customized three op-amp approach. It is a high precision, low-power general purpose amplifier. An active high pass filter and an active low pass filter have been designed to operate in the cutoff frequency range of 1-100 Hz.

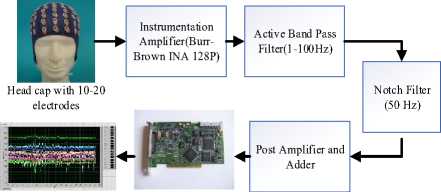
EEG Signal

NI-DAQ Card

Fig.2. Block diagram of EEG signal conditioning system

For removing the 50 Hz power-line interference, a notch filter has been designed for better performance. A post amplifier for further amplification of the EEG signal and a voltage adder circuit has been designed for keeping the signal in positive domain.

• C.    Hidden Markov Model (HMM)

A hidden Markov model (HMM) is a state machine with two layers, namely state layer and observation layer (Fig.3). An HMM model is defined by three probability matrices- initial, transition and emission probabilities. The initial probability is defined as the probability of each state in the beginning of the Marcovian process. The transition probability defines the probability of shifting from one state to another (or the same state) in a particular sequence. The emission probabilities define the probability of a certain observation symbol X ; , in state S ; .

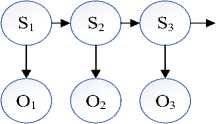
Fig.3. A HMM model with n states (S) and observation sequences (O).

In standard HMMs, at a certain time, say t , all the needed information of the previous states (before t ) would be known by using a discrete hidden state. For a sequence of n elements, say Q , where, Q = {q i ,q 2 ,q 3 ,-q n }and

P(q n lq n-i ,q n-2 ,-,q2 ,q1) = P(q n l4 n-1 )    (1)

Equation (1) is called the first order Markov assumption, where, the probability of observation of a symbol, q_n at time n depends only on observation of q_n-1at time (n - 1) .

An HMM model is specified by

• a)    the (hidden) state sequence S = {s 1 , s₂,s₃, ... s _n };

• b)    the observation sequence X = {x 1 , x₂,x₃,... x_n};

• c)    a set of parameters, 0 = (я, Л, 5) where,

я = a vector of initial probabilities of each state,

Л = a matrix of transition probabilities,

• 5    = a vector of probabilistic output matrix Mathematically,

П = p (s; at t = 0)(2)

a;j =  P (Sj at t + 1| s; at t)(3)

bi(x) = p (0t = x| st at t)(4)

Where, x = observed signal value;

s = state of the HMM model

The output function B is a Gaussian density function.

1       ¹Г ^-M g 2

' ^nO ,7.^     . ..„.^{6 с ]}

Where,

О = sequence of observation;

ц = mean of the sequence;

a = standard deviation of the sequence

However, the input state sequences are unknown in our current study.

For a given 9 we have:

р(Х 1 ,х₂,Х з ,^х_п | 9) = p(xJ 9)......p(% n l (6)

Since each observation value X/ is independent.

For each sequence X :

р(х|9) = Z _s p(x,s|9)           (7)

The sum is taken over all hidden state paths s.

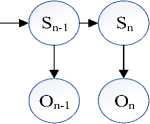
We are intended to include the Baum-Welch algorithm in the HMM model for the parameter estimation when state paths are unknown (Fig.4). This is basically an Expectation Maximization algorithm in the iterative process of HMM. When the states are known, we can simply count. However, when the states are unknown, the ‘counting’ process is little trickier. In such cases the ‘average’ process is employed. For each edge, the ‘average’ number is computed for all possible pairs of given states [25].

L no. unknown states

Fig.4. Unknown state path with known observation sequence.

Three main problems have to be addressed for real world applications of the HMM model.

Problem 1

The       observation       sequence        X =

{X1, X2, X3, ... X_n} and the model 9 = (я, A, 5) are given. The researchers have to find out the best and convenient way for computation of the probability of the observation sequence, p(x | 9). This is called Evaluating. Problem 2

The second step involves to find out the sequence of the states, 5 = {S1, S2, S3, ... S _n} . This problem is known as Decoding.

Problem 3

The third step involves the adjustment of the HMM model parameter, 9 to maximize p(x | 9). This is known as Training.

• D.    Baum-Welch (B-W) Algorithm

Actually the Baum-Welch training is an expectation maximization algorithm suitable for HMM classification when the input states are unknown. We start with some initial values of transition and emission probabilities which define prior values of 9. Then we use an iterative algorithm which attempts to replace 9 by 9 * such that

p(x|9*) > p(x|9)             (8)

Where, x is the observation state;

• 9    = Initial parameters (я, A, 5);

• 9    *= Updated parameters (я, A, 5);

A Markov chain over a set of (hidden) states, and for each state s and observable symbol X , an emission probability p (X _; = x| 5 = s) . An HMM model is defined by the parameters: a _kl (transition probabilities) and e _k (6) (emission probabilities) for all states k, Z and all symbols 6 as shown in Fig.5. The B-W algorithm will be operated in two steps, namely, the E step and the M steps.

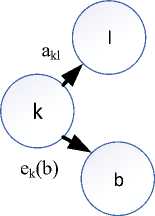
Fig.5. HMM parameters estimation

The E Step

p(X7)=Probability of observation of a particular symbol, X7;

L = No. of total edges, S / _-1 ^ S / .

Expected no. of symbol emissions for state k and each symbol 6, for each Z, compute the expected no of times that X _; = 6, E_k(6),

The M Step

New values of a_kl and e _k (b) after each iteration define 0 and are computed using A_kl and E _k(6) from the E step respectively:

aki =     and ek(b) = -M-     (H)

^kl     ^ lr A_kl ,         ^{kV j}    I. b, E k (b-)          ^{v 7}

• E.    Data Description

The EEG signals of 130 subjects whose ages are in the range of 10-100 years have been collected for this study from the Temple University Hospital (TUH) EEG Corpus- a big data resource for automated EEG interpretation [26]. The EEG signals used in this study, have been recorded using several generations of NicoletTM EEG recording technology. The number of channels vary between 24 and 36 channels sampled at 250 Hz frequency. The acquired signals are digitized using 16 bit A/D converter [26]. Each EEG file contains about 20 Mbytes of data stored in an European Data Format (EDF+) file format. Later, EDF+ format has been converted to cell data [27]. These EDF files contain a header with 24 unique fields that contains patient’s information and signal’s conditions such as amplitudes, frequency, no of channels etc. Selected fields of this header is shown in Table 1.

Table 1. Selected Fields From An Edf Header

Field	Description	Example
1	Version Number	0
2	Patient ID	TUH123456789
4	Gender	M
6	Date of Birth	57
8	Firstname Lastname	TUH123456789
11	Startdate	01-MAY-2010
13	Study Number/ Tech. ID	TUH123456789/TAS X
14	Start Date	01.05.10
15	Start time	11.39.35
16	Number of Bytes in Header	6400
17	Type of Signal	EDF+C
19	Number of Data Records	207
20	Dur. of a Data Record (Secs)	1
21	Number of Signals in a Record	24
27	Signal Prefiltering	HP:1.000Hz       LP: 70.0Hz N: 60.0
28	No. of Signal Samples/Rec.	250

6-way classification is focused on the collected EEG signals:

• a)    SPSW:

SPSW stands for Spike and/or Sharp Wave which demonstrates epileptiform transients. Patients with epilepsy have this type of waveform.

• b)    PLED:

The full form of PLED is Periodic Lateralized Epileptiform Discharges which shows EEG abnormalities such as repetitive spike or sharp wave discharges over one hemisphere at almost fixed time intervals.

• c)    GPED:

GPED stands for Generalized Periodic Epileptiform Discharges which provide both short and long interval periodic diffuse discharges along with suppression burst patterns according to interval between discharges. Triphasic waves are included in this class.

• d)    ARTF:

ARTF means artifacts that represent noises in the EEG signals due to equipment, environment or movement of the subjects.

• e)    EYEBL:

EYEBL means eye blinks which is often be confused with a spike.

• f)    BCKG:

BCKG means background which includes all other signals.

The first three classes describe those information which are required in manual interpretation, periodic and occur across the channel. The last three classes are necessary for background modelling which attempts to model the signal temporal evolution.

• F.    Experiment

In this experiment, 5 states, namely, Epilepsy, Seizure, Stroke, Dementia and Normality are defined with the following transition probability from one state to the next (Fig.6). As we see, the transition probabilities are all equal initially due to the fact that all states are equiprobable. It indicates that a subject may belong to any of the 5 states equally likely depending on his/her EEG signal.

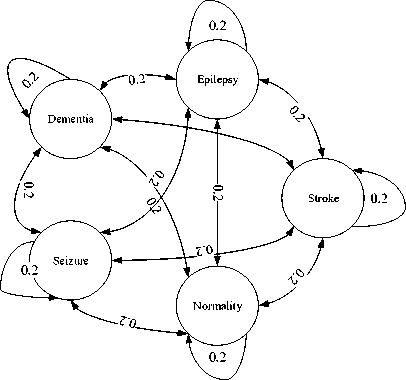
Fig.6. State transition diagram of the HMM

However, the initial probability matrix remains constant while the elements of transition probability matrix, aM and emission probability matrix, ek(b) are updated after each iteration as given in Equation 11. In proposed methodology, the HMM parameters (transition and emission matrix) are undergone repetitive iterations until a certain threshold is met. This threshold is determined by Equation 8 which is the outcome of expectation maximization algorithm. The initial probability for each of the 5 states is same (0.2). It means subject no= 1 may belong to any of the 5 states as defined above. The states of the next subjects, subject no = 2, 3, 4, 5,… …up to the last subject, depends on the states of their exact previous subject as first order Markov assumption is applied (Equation 1). The states of the subjects are determined from the observation sequence. The algorithm and flowchart used in this study are represented here where the steps are followed sequentially.

Step 1:

Define number of states and the HMM parameter

е (л,А,ву

Step 2:

Collection of EEG signals from the subjects using 24 to 36 channels

Step 3:

Sample the EEG signals at sampling frequency = 250 Hz and represent each sample using 16 bits.

Step 4:

Run the HMM model with the initial value of е (л, А, В) [Equation 2,3,4].

Step 5:

Update е to е * after each iteration using the B-W algorithm [Equation 9,10.11].

Step 6:

Check the threshold р(х|е *) > р(х|е) [Equation 8] after each iteration. If it satisfies then collect hidden and observation sequences. If not satisfies then go to Step 4.

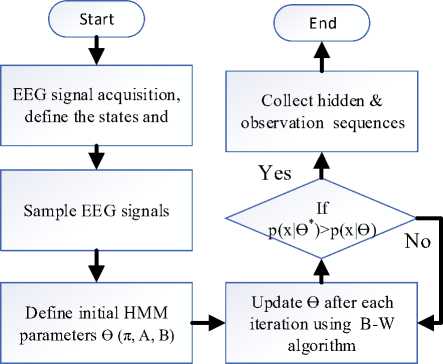
Fig.7. Flowchart of the proposed algorithm.

• III.    Result Analysis

The task to adjust the HMM model parameter, ϴ to maximize the likelihood of the observation sequence is known as the training phase [27]. The B-W algorithm is used to address this problem. This study is aimed to classify the EEG signals to detect 4 different brain diseases and the normality condition of 130 subjects. The performance results are shown in Table 2.

Table 2. Performance analysis of the proposed algorithm on 130 subjects

Classifier	States	No  of subjects	Detected as correctly	Sensitivity	Overall accuracy
HMM	Epilepsy	44	44	100%	92.31%
	Dementia	10	8	80%
	Stroke	25	24	96%
	Seizure	41	37	90.24%
	Normal	10	7	70%

Table 3. Performance of other studies on 31 subjects

Classif ier	States	No. of Subject	No. of PD Detected	No.   of Healthy Detected	Sens . (%)	O. A.(%)
HMM	PD	15	14	1	93.3 3	90.32
	Health y	16	2	14
LS-SVM	PD	15	13	2	86.6 7	90.32
	Health y	16	1	15

PD= Parkinson’s Disease O.A.= Overall Accuracy Sens.=Sensitivity

In Table 3, the performance of two other classification studies using HMM model [28] and LS-SVM method [29] has been shown. Two statistical parameters, namely, sensitivity (the percentage of correctly detected subjects on their respective states) and accuracy (the overall percentage of correctly detected subjects) are used for the evaluation of different classification schemes. The proposed method provides better performance than the previous studies on several reasons. There are 5 different states and 130 subjects are examined in this study (Table 2) compared to 2 states and 31 subjects on other studies (Table 3). As the HMM is actually a probabilistic distribution method, the accuracy and sensitivity increase with an increase in number of subjects. Moreover, the proposed method in Table 2 is suitable for large number of subjects rather than the two schemes of Table 3. The methodology of Table 2 is suitable for large scale diagnosis purposes. The sensitivity of epilepsy (100%) and   stroke (96%) are higher than both the studies of

Table 3 (93.33% and 86.67%). The proposed algorithm discusses the most occurring 4 brain diseases whereas both the studies of Table 3 discuss only 1 disease, Parkinson’s disease. So, proposed method is likely to be more suitable for detection of different brain diseases in a large scale. However, the lower sensitivity of dementia and normality is due to lower number of subjects. The overall accuracy is 92.31% in Table 2 which is larger than both the methods (90.32%) showed in Table 3.

• IV.    Conclusion

• V.    Future Work

• [1]    M. Lasfar, H.Bouden, “A method of data mining using Hidden Markov Models (HMMs) for protein secondary structure prediction,” Procedia Computer Science 127, pp. 42-51, 2018.

• [2]    R. Mouhcine, A. Mustapha, M. Zouhir, “Recognition of cursive Arabic handwritten text using embedded training based on HMMs,” Journal of Electrical Systems and Information Technology 5, pp. 245-251, 2018.

• [3]    A.S. Dhawan, J. Kosecka, H. Rangwala, S. Sikdar, “An intuitive muscle-computer interface using ultrasound sensing and Markovian state transitions,” 2018 IEEE 15^th International Symposium on Biomedical Imaging, April 47, 2018.

• [4]    J. Li, T. Lei, F. Zhang, “An Gaussian-Mixture Hidden Markov Models for Action Recognition Based on Key Frame,” 11^th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), 2018.

• [5]    H. Tan, P. Fischer, S. A. Shah, D. Vidaurre, M. W. Woolrich, P. Brown, “ Decoding Movement States in Stepping Cycles based on Subthalamic LFPs in Parkinsonian Patients,” IEEE, pp. 1384-1387, 2018.

• [6]    E. Rabhi, Z. Lachiri, “Personal identification system using physiological signal,” IEEE 4^th Middle East Conference on Biomedical Engineering (MECBME), pp. 153-158, 2018.

• [7]    T. A. W. Bolton, A. Tarun, V. Sterpenich, S. Schwartz, D. M. D. Ville, “Interactions Between Large-Scale Functional Brain Networks are Captured by Sparse Coupled HMMs,” IEEE Transactions on Medical Imaging, Vol. 37, No. 1, pp. 230-240, January 2018.

• [8]    D. Oletic, V. Bilas, “Asthmatic Wheeze Detection from Compressively Sensed Respiratory Sound Spectra,” IEEE Journal of Biomedical and Health Informatics, 2017.

• [9]    I. Sgouralis, S.Presse, “An Introduction to Infinite HMMs for Single-Molecule Data Analysis,” Biophysical Journal 112, pp. 2021-2029, May 23, 2017.

• [10]    S. Ghosh, J. Li, L. Cao, K. Ramamohanarao, “Septic shock prediction for ICU patients via coupled HMM walking on sequential contrast patterns,” Journal of Biomedical Informatics 66, pp. 19-31, 2017.

• [11]    M. H. Rahmani, F. Almasganj, “Lip-reading via a DNN-HMM Hybrid System Using Combination of The Imagebased and Model-based Features,” 3^rd International Conference on Pattern Recognition and Image Analysis, pp. 195-199, April 19-20, 2017.

• [12]    S. Yu, H. Chen, R. A. Brown, “Hidden Markov ModelBased Fall Detection with Motion Sensor Orientation Calibration: A Case for Real-Life Home Monitoring,” IEEE Journal of Biomedical and Health Informatics, 2017.

• [13]    K. Guo, H. Candra, H. Yu, H. Li, H. T. Nguyen, S. W. Su, “EEG-based Emotion Classification Using Innovative Features and Combined SVM and HMM Classifier,” IEEE, pp. 489-492, 2017.

• [14]    T. Yang, W. Huang, Z. Jiang, C. K. Chui, L. Jiang, “ Stacked Hidden Markov Model for Motion Intention Recognition,” IEEE 2^nd International Conference on Signal and Image Processing, pp. 266-271, 2017.

• [15]    M. Mohammadpour, V. Rahmani, “A Hidden Markov Model-Based Approach to Removing EEG Artifact,” 5^th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), pp. 46-49, 2017.

• [16]    J. Wahlstrom, I. Skog, P. Handel, F. Khosrow-khavar, K. Tavakolian, P. K. Stein, A. Nehorai, “A Hidden Markov Model for Seismocardiography,” IEEE Transactions on Biomedical Engineering, 2017 .

• [17]    S. M. Bhatti, M. S. Khan, J. Wuth, F. Huenupan, M. Curilem, L. Franco, N. B. Yoma, “Automatic detection of volcano-seismic events by modeling state and event duration in hidden Markov models,” Journal of Volcanology and Geothermal Research 324, pp. 134-143, 2016.

• [18]    J. C. Kao, P. Nuyujukian, S. I. Ryu, K. V. Shenoy, “A high-performance neural prosthesis incorporating discrete state selection with hidden Markov models,” IEEE Transactions on Biomedical Engineering, 2016.

• [19]    C. Song, K. Liu, X. Zhang, L. Chen, X. Xian, “An Obstructive Sleep Apnea Detection Approach Using a Discriminative Hidden Markov Model from ECG Signals,” IEEE Transactions on Biomedical Engineering, 2015.

• [20]    P. Ambrosini, I. Smal, D. Ruijters, W. J. Niessen, A. Moelker, T. V. Walsum, “A Hidden Markov Model for 3D Catheter Tip Tracking With 2D X-ray Catheterization Sequence and 3D Rotational Angiography,” IEEE Transactions on Medical Imaging, Vol. 36, pp. 757-768, March 2017.

• [21]    K. M. Vamsikrishna, D. P. Dogra, M. S. Desarkar, “Computer-Vision-Assisted Palm Rehabilitation With Supervised Learning,” IEEE Transactions on Biomedical Engineering, Vol. 63, pp. 991-1001, May 2016.

• [22]    R. V. Andreao, B. Dorizzi and J. Boudy, "ECG signal analysis through hidden Markov models," in IEEE

  Transactions on Biomedical Engineering , vol. 53, no. 8, pp. 1541-1549, Aug. 2006.

• [23]    N. Naseer, K.S. Hong, “fNIRS-based brain-computer interfaces: a review”, Frontiers in Human Neuroscience , Volume 9, Article 3, pp. 6-7, January 2015.

• [24]    L.M. Hirshfield, “Combining Electroencephalograph and Functional Near Infrared Spectroscopy to Explore Users” Mental Workload. In: Schmorrow D.D., Estabrooke I.V., Grootjen M. (eds) Foundations of Augmented Cognition. Neuroergonomics and Operational Neuroscience. FAC 2009. Lecture Notes in Computer Science, vol 5638. Springer, Berlin, Heidelberg.

• [25]    Yuzhen Ye, “HMM: Parameter Estimation”, I529: Machine Learning in Bioinformatics , pp. 14-23, Spring 2013.

• [26]    A. Harati, S. López, I. Obeid, J. Picone, M. P. Jacobson and S. Tobochnik, "The TUH EEG CORPUS: A big data resource for automated EEG interpretation," 2014 IEEE Signal Processing in Medicine and Biology Symposium (SPMB) , Philadelphia, PA, 2014, pp. 1-5.

• [27]    A. Khorasani, M.R. Daliri, “HMM for Classification of Parkinson’s Disease Based on the Raw Gait Data”, J Med Syst. 2014 Dec;38(12):147

• [28]    Y. Wu and S. Krishnan, "Statistical Analysis of Gait Rhythm in Patients With Parkinson's Disease," in IEEE Transactions on Neural Systems and Rehabilitation Engineering , vol. 18, no. 2, pp. 150-158, April 2010.

• [29]    B. Resch, “Hidden Markov Models: A Tutorial for the Course Computational Intelligence”, Signal Processing and Speech Communication Laboratory , Inffeldgasse 16c, pp.1-14.

• [30]    A. Gabell, U. Nayak, “The effect of age on variability in gait”, Journal of Gerontology , vol. 39, no. 6, pp. 662-666, 1984.